Neural Networkベースのグラフembedding手法の紹介

こんにちは、次世代システム研究室のA.Zです。

はじめに

グラフの構造や理論は多く分野に応用されています。SNSは人と人のつながりは巨大なグラフで表現することできます。通信ネットワークの構造やルート自体は根本的にグラフになっています。また、量子アニーリングコンピュータの分野でも、解決したい問題はほとんど先にグラフに表現してから、Ising modelに変換し、量子コンピュータに実行させます。

グラフの幅広いの応用分野と柔軟性と高い表現力の性質を持っているため、機械学習の分野、特にneural networkにも不可欠になっています。最近、グラフを応用した機械学習の技術や研究は増加しています。昨年、AIのメジャーな学会、NeurIPS(Neural Information Processing Systems) 2019で、neural networkや機械学習を応用するグラフの研究の論文は100件以上超えています。いよいよneural networkにグラフデータの応用は注目され始めていると思います。

今回、上記のきっかけで、neural networkにおけるグラフデータの応用について紹介したいと思います。

Neural Networkにグラフデータ応用について

Neural networkに、グラフデータを利用するには一番一般的な手法はグラフデータをvectorに変換することです。
こちらの手法はグラフ Embeddingと呼ばれます。Neural Networkのグラフ embeddingは基本的に2つやり方があります。

1. グラフ embeddingをPre-Processingの処理のステップで行います。
   こちらのアプローチは本題の学習モデルから、embeddingの処理は完全に切り離します。embeddingの処理は基本的に前処理(Pre-Processing)の段階で行い、その結果は本題の学習モデルにフィーチャーとして入れます。
   こちらアプローチのメリットはグラフembeddingのアルゴリズムは本題の学習モデル完全に独立のため、利用するアルゴリズムは自由に選択できます。一方、デメリットはembedding処理と本題学習モデルは連携できず、同時にembeddingと本題の学習モデルの最適化ができません。それぞれの最適化が必要のため、効率が悪いです。
2. グラフ embeddingをNeural Network構造の中に行います。
   こちらのアプローチは本題の学習モデルの中に、embedding処理を組み込みされます。このアプローチのメリットは本題の学習モデルが最適化されてたら、自動的にembeddingの部分も最適化されるので、効率が良いです。更に、embeddingと他のfeatureが同時に学習するため、グラフの構造情報だけではなく追加情報も利用されるので、全体のモデル精度的に(1)より良いです。デメリットとしては本題の学習のneural networkモデルに依存するため、embedding手法は限られています。

グラフのコンポネントから、どれかをembeddingするかによって、大きく2つの種類があります。

1. Vertex(Node) embedding
   こちらはある問題やタスクドメインを一つのグラフの表現し、グラフの中にあるnodeの関連性考慮しをvectorに変換することです。
2. グラフ embedding
   こちらは全体的なグラフをvectorに変換することです。こちらのアプローチはグラフレベルの予測やグラフ全体をfeature化したいときに使います。例えば、生物の分野であるタンパク質(protein)の様々性質の構造は一つグラフとして表現し、embeddingするときに、そのグラフをembeddingします。

現在、Vertex embeddingは一番良く使われています。Vertex embeddingの中に、いくつかのアルゴリズムがあります。前回、すでにrandom walk応用したembedding手法(node2vec)が紹介されました。今回はAutoencoderの手法応用したStructural Deep Network Embedding(SDNE)のembeddingを紹介したいと思います。

https://www.kdd.org/kdd2016/papers/files/rfp0191-wangAemb.pdf

node2vecの手法は基本的にpre-processingのステップでembeddingの行い、一方、SDNEは本題学習のneural networkに、そのまま組み込みできます。

SDNEについて

Structural Deep Network Embedding(SDNE)はAutoencoderを利用したグラフ embedding手法です。

こちらの手法の特徴はグラフの中にあるノードとノードの関係(1st order proximity)とノードの近所の情報(2nd order proximity)を保つすることができます。ノードとノード間に繋がっていれば、基本的にその二つのノードが似ています。また、二つのノードの間に、似たような近所情報持っていれば、その二つのノードが似ています。その二つの条件を満たすために、SDNEは以下のようにネットワーク構造で、構成されています。

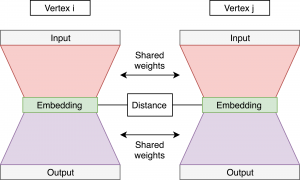
赤い部分はEncoder, 紫の部分はdecoderになっています。Encoderで、embedding vectorを生成し、その結果をdecoderにinputし、元のinputデータを再現できるようにという処理です。学習自体はedge単位で行い、そのedgeに構成される各ノードが同時にautoencoderに入れます。Inputデータは各ノードの近所情報(adjacent matrix)になっています。各の同時学習行うことで、ネットワークの重みパラメータは共有可能になり、各ノードの近所情報は学習できます。これによって、embedding結果はノードの近所の情報(2nd order proximity)を維持することができます。こちらのencoderの学習をコントロールするために、autoencoderのloss関数（reconstruction loss or Loss2)は以下に定義されています。

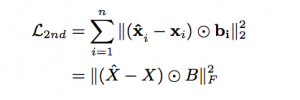
上記のloss関数は基本的にautoencoder output(x’)とautoencoder input(x)の差、掛けるbという条件付きの値のmean square errorになっています。bの値は基本的に近所の情報の差の部分だけをもっとpenaltyの重みを大きくするように調整します。こちらのloss関数を利用すれば、ノードの近所の情報は維持することができます。また、似たようなノードだったら、embeddingの結果も似ていますという原理から元に、ノード間の繋がりを維持する為に、以下のloss関数(embedding loss or Loss1 )定義されます。

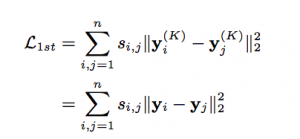
上記の式の中にsはedgeの重みになっています。yiとyjはnode iとjのembedding結果です。学習処理で、Loss1とLoss2を組み合わせて、最適化すればノード間の情報とノードの近所情報と維持できるグラフembeddingが実現できます。コンセプト自体はそんなに難しくないが精度が良い為、応用しやすいではないかと思う理由に、こちらの手法を選びました。

実験

データセットについて

今回の実験で利用しているデータセットはIMDB-BINARYのデータセットになっています。データセット自体は以下のURLからダウンロードできます。

https://ls11-www.cs.tu-dortmund.de/staff/morris/graphkerneldatasets

IMDB-BINARYはIMDBの映画のデータから、同じ映画で出てきた俳優のグラフを表しています。各ノードは俳優を表し、同じ映画で、出たら、その俳優のノードがつながっています。こちらのデータは二つのカテゴリ、アクションとロマンスから作成されたものです。
データの詳細内容(nodeの数、edgeの数など）は上記のURLで確認できます。

実装コード

実装コード自体は一般的に使われているpython,keras, tensorflowの利用し、実装しました。

今回の実験の実装コードは以下のrepositoryをベースし、実装行います。

https://github.com/xiaohan2012/sdne-keras

loss関数の定義

import keras
from keras import Model, backend as K, regularizers
from keras.layers import Dense, Embedding, Input, Reshape, Subtract, Lambda

### 特定ノードのembedding結果(encode)から、再構築(decode)後結果にたいするloss関数
def build_reconstruction_loss(beta):
    assert beta > 1

    def reconstruction_loss(true_y, pred_y):
        diff = K.square(true_y - pred_y)

        weight = true_y * (beta - 1) + 1

        weighted_diff = diff * weight
        return K.mean(K.sum(weighted_diff, axis=1))  # mean square error
    return reconstruction_loss

## つながっているnodeの間にのembedding結果lossの定義
def edge_wise_loss(true_y, embedding_diff):
    return K.mean(K.sum(K.square(embedding_diff), axis=1))  # mean square error

モデル構造の定義

embedding_dim=100 # グラフ embeddingの次元数
nodes_count=xxx # グラフのnodeの数
alpha = 2 # グラフのedge重みのlossのパラメータ。今回は重みグラフを使っていないので、結果が影響がない。

# one end of an edge (adjacency matrix. shape=(1,nodes_count))
input_a = Input(shape=(1,), name='input-a', dtype='int32')
# the other end of an edge (adjacency matrix. shape=(1,nodes_count))
input_b = Input(shape=(1,), name='input-b', dtype='int32')
# edgeの重み
edge_weight = Input(shape=(1,), name='edge_weight', dtype='float32')

encoding_layers=[]
decoding_layers=[]

#encoding
layer = Dense(embedding_dim, activation='sigmoid',
                kernel_regularizer=regularizers.l2(l2_param),
                name='encoding-layer-{}'.format(i))
encoding_layers.append(layer)

# decoding
# 最終的なdecoderのoutputはあるノードの構造(adjacency matrix)になって、decoder output dimはノードの数と同じ
layer = Dense(
    nodes_count, activation=activation,
    kernel_regularizer=regularizers.l2(l2_param),
    name='decoding-layer-{}'.format(i))
decoding_layers.append(layer)

all_layers = encoding_layers + decoding_layers

encoded_a = reduce(lambda arg, f: f(arg), encoding_layers, input_a)
encoded_b = reduce(lambda arg, f: f(arg), encoding_layers, input_b)

decoded_a = reduce(lambda arg, f: f(arg), all_layers, input_a)
decoded_b = reduce(lambda arg, f: f(arg), all_layers, input_b)

embedding_diff = Subtract()([encoded_a, encoded_b])

# add weight to diff
embedding_diff = Lambda(lambda x: x * edge_weight)(embedding_diff)

self.model = Model([input_a, input_b, edge_weight],
                [decoded_a, decoded_b, embedding_diff])

reconstruction_loss = build_reconstruction_loss(beta)

self.model.compile(optimizer='adadelta',
                loss=[reconstruction_loss, reconstruction_loss, edge_wise_loss],
                loss_weights=[1, 1, alpha])

結果

こちらの実験の目的はSDNEのembeddingの結果を直感的に調査すること。
基本的に、同じカテゴリのグラフはvectorに変換するときに、近く集まっていまる。
embeddingした結果、2次元のT-SNEでplotしてみました。

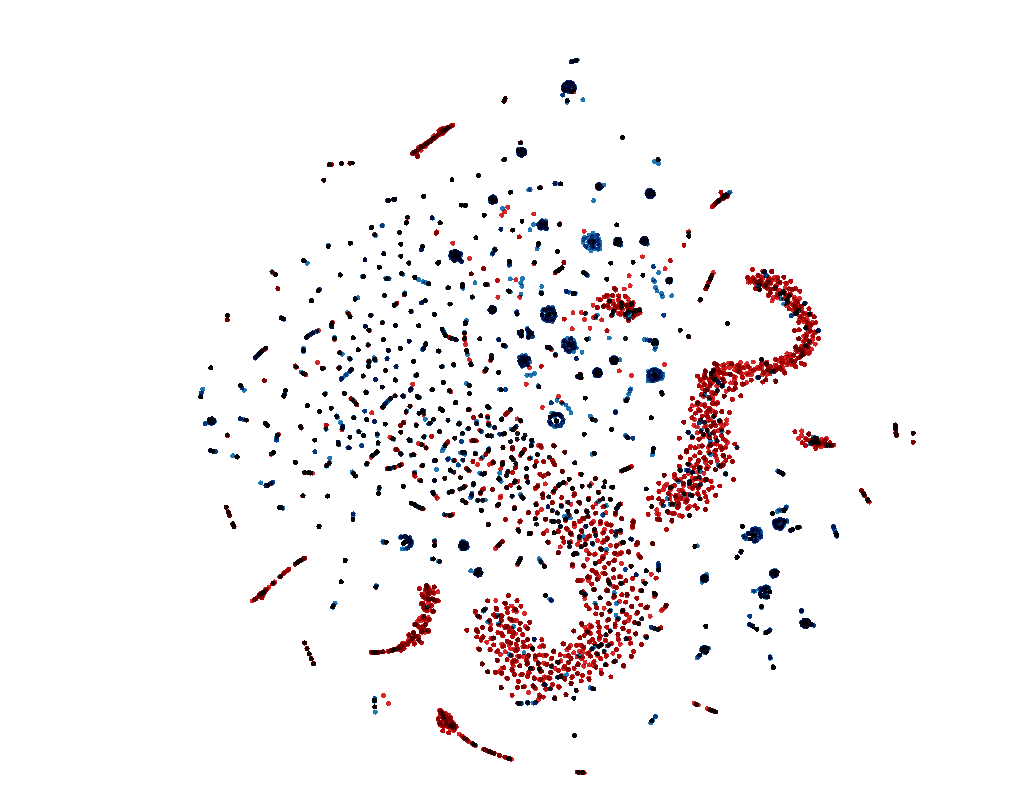
上記の結果からみると、T-SNEの次元不足の影響で、きれいに別れていないところありますが、赤い点と青い点はなんとなく分類はできているかと思います。実際に100次元の空間になると、分類精度はもっと良いではないかとおもいます。

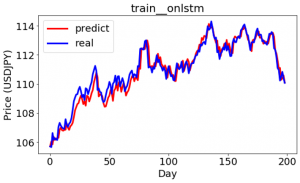
Trainingのloss(3 epoch) は以下のようになっています。

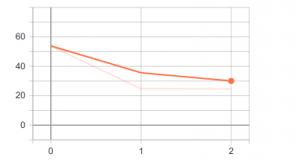
上記から、epochをもっと増やすと、まだlossが下がりそうだと思います。精度がまだ改善できると思います。また、更にparameter tuningすれば、精度はもっと改善できるではないかと思います。

まとめ

• 今回はneural networkにグラフembedding様々なアプローチや種類を紹介いたしました。
• グラフembeddingの手法中に、SDNEという手法について紹介いたしました。実験した結果から、精度は期待できると思います。更に、アルゴリズム自体はシンプルで、応用しやすいと思います。
• 今後、グラフembedding自体はneural networkモデルに組み込み、end-to-endモデルも試してみたいと思います。
• 今まで、neural networkにグラフデータを応用する研究のテーマは荒削という印象がありましたが、昨年より、このテーマかなり注目され、これからは展開し、もっと流行するではないかと思います。

最後に

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。