有意性は統計検定の全てではない～効果量のバイアスが補正できるか
こんにちは、次世代システム研究室のC.Z.です。
最近は統計検定に関する新しい論文を読みましたので、それをテーマとして基本から簡単に紹介したいと考えます。
はじめ
この前はベイズ統計について紹介・実践したことがありますが、現在は学界でもデータ解析関連の業界（機械学習も勿論）でも、伝統的な統計学推定は未だ圧倒的に使われている手法です。なので、今回の記事はベイズ統計学と伝統的統計学の比較（どれがいい）をするつもりがなくて、ただ伝統的な統計手法の注意点と問題点について話したいと思います。伝統的な統計学（すなわちfrequentist）の手法といえば、以下の基礎仮定と推定流れがあります：
- 統計量に対して帰無仮説（NULL hypotheses）が存在する
- この帰無仮説が正しいまたは間違えのいずれになる
- 帰無仮説の正しさのテストにおいて第一種過誤と第二種過誤も必ず出てくる
第一種過誤と第二種過誤
データ解析関連の人間なら、だれでも聞いたことがある専門用語と思いますが、一応復習しておきます。まず、別記事のイラスト図を借りて、見てみます。
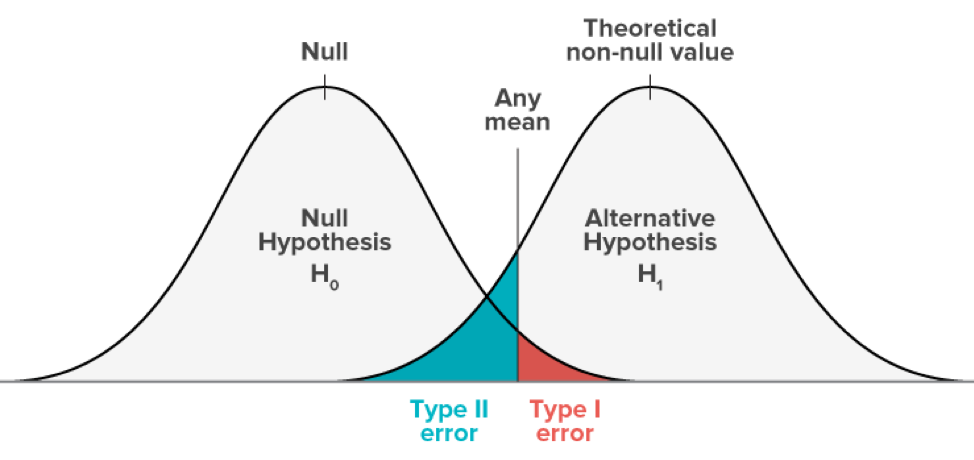
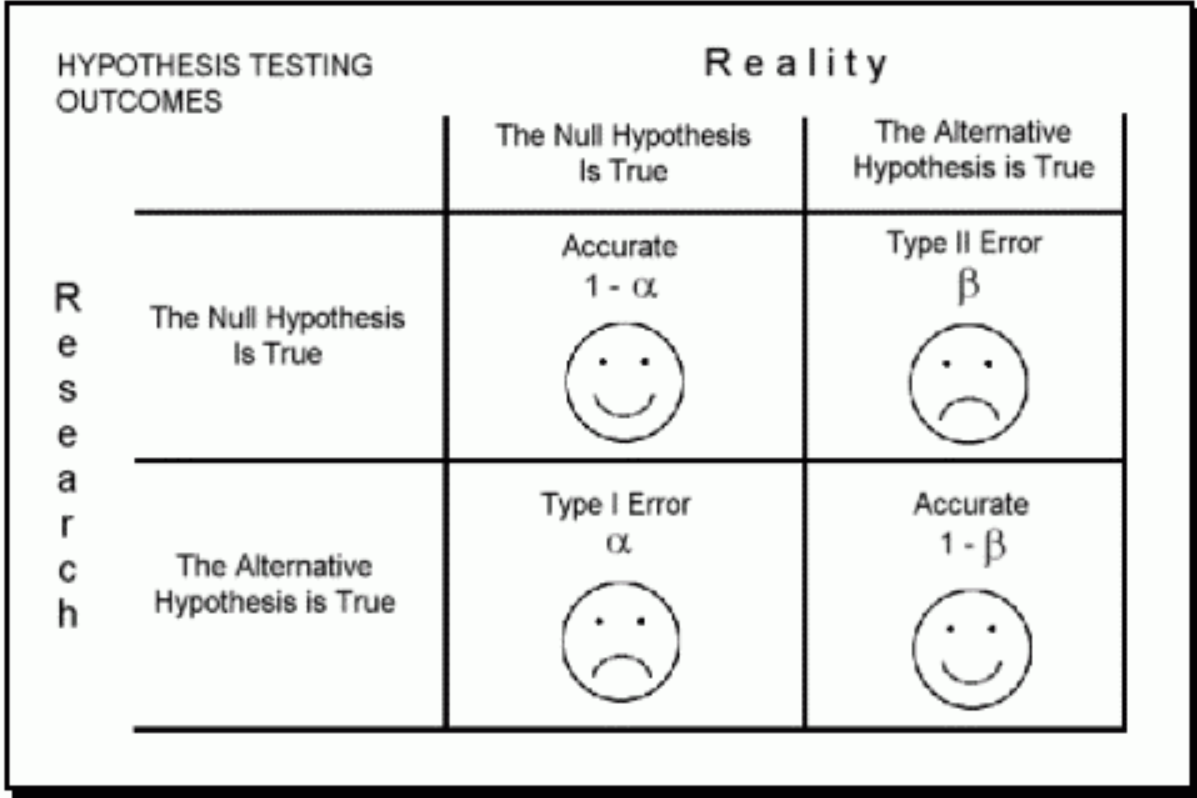
つまり、有意水準Alphaを設定しておいて、テストを行います。点推定の場合、上記４つの結果の１つしか当たることができません。
- もし帰無仮説を拒否したら、第一種過誤を起こす可能性が出てくる；
- 一方で、もし帰無仮説を受け入れるなら、第二種過誤を起こす可能性が出てくる。
- 二つ分散が既知の正規分布がある
- 分布Aの平均値が分布Bの平均値より大きい
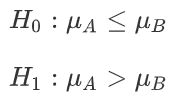
第一種過誤はAlphaそのものです：
import numpy as np from numpy.random import randn from scipy.stats import norm, truncnorm np.random.seed(36) alpha, n, sigma, nsim = 0.05, 25, 2, 100000 c_alpha = norm.ppf(1-alpha) err1 = np.mean([ (np.mean(randn(n)) - np.mean(randn(n)))/np.sqrt(sigma/n) > c_alpha for i in range(nsim)])
第二種過誤は比較的に直感的ではないですが、上記イラスト図のように、緑の部分に落ちますと、第二種過誤を起こしました：
diff_in_anb = 0.6 beta = norm.cdf(c_alpha - d / np.sqrt(2/n)) err2 = np.mean([ (np.mean(d + randn(n)) - np.mean(randn(n)))/np.sqrt(sigma / n) < c_alpha for i in range(nsim)])
有意性は統計検定の全てか？
現在の実態は、伝統統計学手法の応用上がほぼ検定の有意性だけに注目するになります。特にアカデミックの論文なら、自分の「都合がいい」結論に裏付けるため、不正misconductを排除しても、結果の再現性も非常に問題になります。なぜなら、統計検定が有意であること（いわゆる第二種過誤を回避した）は、どのくらいの確率で第二種過誤を回避できるかということが全く保証できないです。
この確率は検定の検定力（power）と呼びます。すなわち、上記の（1-Beta）です。
以下の研究によりますと、
We investigate two critical dimensions of the credibility of empirical economics research: statistical power and bias. We survey 159 empirical economics literatures that draw upon 64,076 estimates of economic parameters reported in more than 6,700 empirical studies. Half of the research areas have nearly 90% of their results under‐powered. The median statistical power is 18%, or less. A simple weighted average of those reported results that are adequately powered (power ≥ 80%) reveals that nearly 80% of the reported effects in these empirical economics literatures are exaggerated; typically, by a factor of two and with one‐third inflated by a factor of four or more.
つまり、6700以上の研究の中で、テストが有意であっても、検定パワーの中央値はただ18%しかありません。80%以上の結果がunder-powerかつ誇張評価になりまして、実証や理論の再現の難しさがわかりました。
但し、80%以上の推定検定力を持つことと言っても（例えば、生物や医学の分野なら、検定力も重視されている）、Betaが人間によりコントロールできるものなので、研究者は常に楽観的な検定力を使う意図がありますし、性能の保障にイコールではないです。
⇔ 第二種過誤率（1-power）：
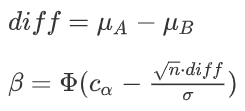
- C_Alphaが小さいほど => 第一種過誤率（Alpha）が大きいほど
- サンプルサイズが大きいほど
- diffが大きいほど
- 分散が小さいほど
なお、上記式の
は効果量（Effect Size）と呼びます。言い換えれば、「パワー」、「サンプルサイズ」、「有意水準」、「効果量（effect size）」の中で、三つが決まれば、残りの一つが分かります。
このような「推定手法」の結果の一つとして、検定の効果量バイアスが生じました。
効果量と効果量のバイアス
効果量のバイアスが、実際は「勝者の呪い」という現象としてよく知られている。別記事の定義を引用します：
勝者の呪いとは、オークションにおいて構造的に生じる現象。国債入札、掘削権オークション、不動産競売などのように、商品の価値について、ある種の共通の市場価値が与えられる商品のオークションを「共通価値のオーション（common values auction）」という。共通価値のオークションにおいては、各プレーヤーがこの転売時の市場価格（商品の共通価値）を予め知ることができず、各自推定しなければならない。その場合、後で決まる商品の転売市場価格を上回った推定をしていたプレーヤーが往々にして落札する（勝者となる）。すなわち、「勝者」である落札者は、商品の共通価値を上回る推定額を出したために落札することができたものの、その価格は転売市場価格を上回っているため、転売することで損失を被ってしまう。このことを「勝者の呪い」という。
すなわち、推定結果が常に過大評価になるバイアスがあります。前述のように、検定力を重視することがこの問題を解決するためのメインな手法です。つもり、効果量のバイアスと検定力が逆相関があります。
「勝者の呪い」を補正するため、過去複数の手法が提出されました。その中で、Andrew GelmanとJohn CarlinがTYPE S(sign)とTYPE M(magnitude) errorという二つのコンセントを定義しまして、現在の研究は基本的に彼らの研究の延長線にあります。
=> 先に効果量のバイアスと検定力を推定して、次に効果量を推定して、結果の評価が最後のステップにします。
調整手法の紹介に入る前に、先ず式より効果量のバイアスと検定力の関係を見てみます。
また上記のシンプル設定を考えます。
diff（二つ分布の差分）が正規分布に従うことを仮定しましたので、diffの有意推定値はtruncated正規分布（上限下限あり→ c_alphaの値）に従うことが分かります。
＝＞ 上限をu、下限をしにします
=>
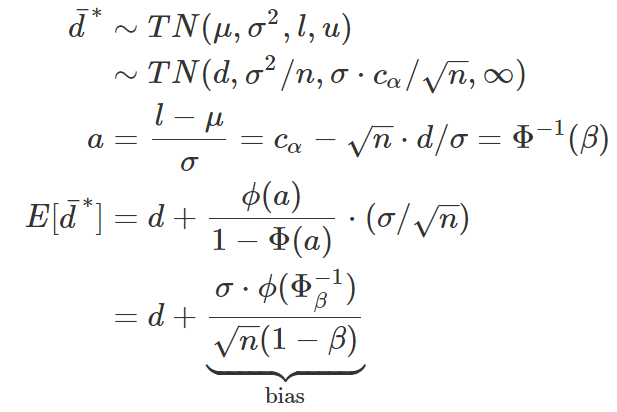
つまり、truncated正規分布のbiasが検定力（1-Beta）を含みます。
さらに、期待値と実際値の比率をバイアスのratioに定義されています。
=> 
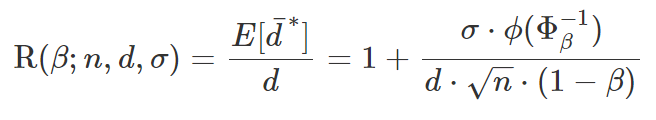
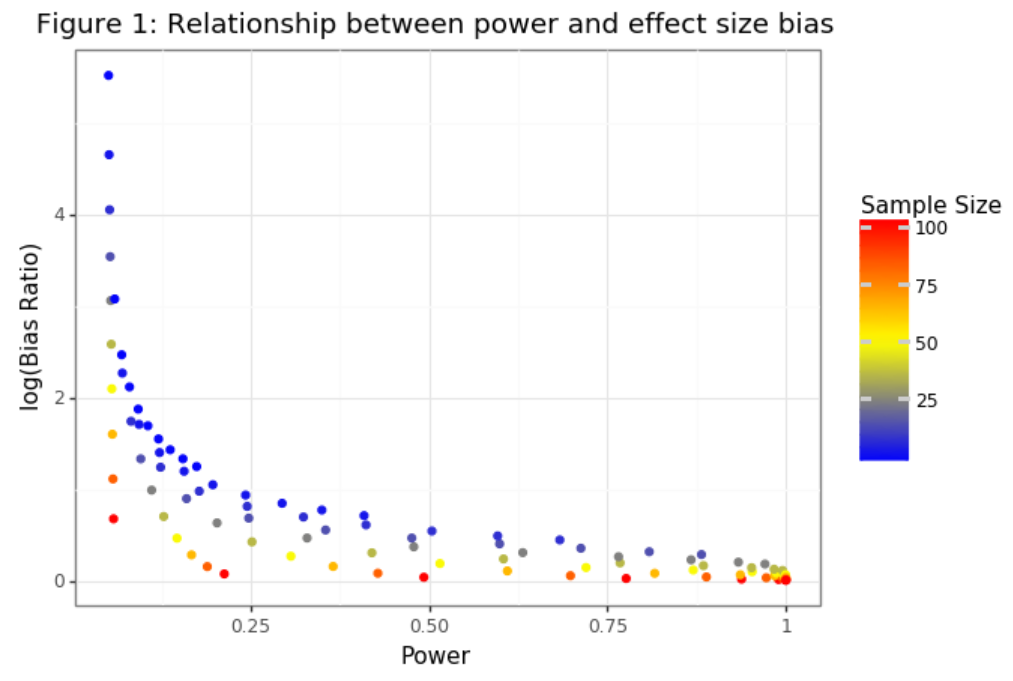
検定力と効果量バイアスの逆相関が見えてきました。=> 検定力が高いほど、バイアスが弱い
効果量のバイアスが補正できるか
まず、truncated正規分布の期待値式を見てみると、以下の定義ができます：def get_truncated_mu(actual_mu, alpha, n, sigma): range = norm.ppf(1-alpha) - sqrt(n)*actual_mu/sigma truncated_mu = actual_mu+ norm.pdf(range)/(1-norm.cdf(range)) * sqrt(n)/sigma return truncated_mu=>
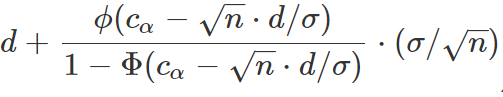
バイアスを低減するため（
を保証したい）、一番保守的な方法はtruncated正規分布の期待値がそのままバイアスを引きますが、問題はdiff>0（対立仮説）とき、バイアスの過剰評価及び本当の効果量の過小評価が発生します。breaks = np.linspace(-1,2,30)
bias_0 = norm.pdf(c_alpha)/(1-norm.cdf(c_alpha))*np.sqrt(sigma/n)
df_bias = pd.DataFrame({'d':d_seq,'deflated':[get_truncated_mu(mu,alpha,n,sigma)-bias_0 for mu in breaks]})
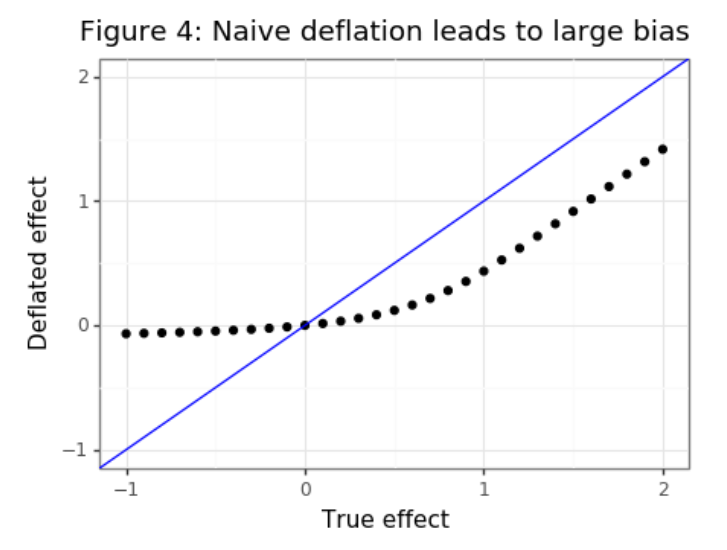
この問題の解決に向けて、ようやく最後の手法を迎えました。特に機械学習の分野でよく見れている補正手法：
＝＞ diff=0の帰無仮説に対して、ペナルティ項をかける
bias_0 = norm.pdf(c_alpha)/norm.cdf(-c_alpha)*np.sqrt(sigma/n)
dist_0 = truncnorm(a=c_alpha,b=np.infty,loc=0,scale=np.sqrt(sigma/n))
sample_0 = dist_0.rvs(size=nsim, random_state=46)
w_0 = dist_0.pdf(sample_0).mean()
sims = []
for i in range(len(breaks)):
dist = truncnorm(a=c_alpha-d/np.sqrt(sigma/n),b=np.infty,loc=d,scale=np.sqrt(sigma/n))
sample = dist.rvs(size=nsim, random_state=46)
deflator = 2*(1-dist_0.cdf(sample))*bias_0
d_adjusted = sample - deflator
df = pd.DataFrame({'adjusted':d_adjusted ,'actual':sample})
sims.append(df )
=>
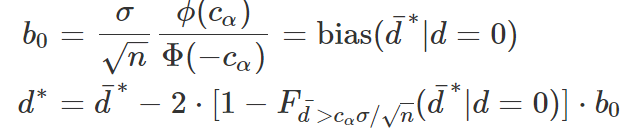
この補正によって、diffが0付近なら強いペナルティを受けますが、0以上なら比較的に弱いペナルティだけを受けることになって、本当の効果量に大分近くになりました。
確かに、十分大きいサイズのサンプル数があれば、安定的な補正効果量推定が得られますが、ペナルティ項の追加によって、新しいノイズが生じまして、理論的には点推定の信頼性にも影響します。
解析結果の再現性と推定性能をもっと向上するため、このテーマについて、将来の研究に注目する価値があるかなと考えます。
最後に
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
