「投資可能 × 解釈可能」：Model Fingerprint

こんにちは。次世代システム研究室のK.S.（女性、外国人）です。

前回は、投資ポートフォリオと資産評価モデルを紹介しましたが、今回はModel Fingerprintsといった金融系の機械学習モデルを解釈するための手法を紹介します。

この手法はmlfinlabがPython libraryとして有料で提供し、月100ポンド（2023年3月末時点では〜16,000円/月）なので、値段の割にどういう価値があるのかが気になっていますので、探って行きたいと思います。

1. Model fingerprints手法

Model fingerprintsは Beyond the Black Box: An Intuitive Approach to Investment Prediction with Machine Learningという論文で紹介されました。この論文では機械学習を用いた投資ポートフォリオにおいて、従来のブラックボックスアプローチより直感的で解釈可能な手法が提案されました。

Model Fingerprintはモデル非依存(Model-Agnostic)のツール（モデルに依存しない説明手法）で、予測変数がグローバルレベルとローカルレベルの両方で予測がどのように貢献しているかのインサイトを提供します。グローバルレベルはモデルの全体像を把握することができ、モデル全体に対する解釈を行うための手法です。一方、ローカルレベルは個々のデータポイントに対する理解を深めることができ、個々のデータ解釈を行うための手法です。

Model fingerprintはPartial Dependenceのコンセプトを拡張し、三つに分けます。その三つとは、各変数の線形効果（Linear prediction effects）、各変数の非線形効果（Nonlinear prediction effects）、各変数のペアの相互作用効果（Pairwise interaction effect）です。まず、Partial Dependenceを復習し、それぞれの手法を紹介していきます。

1.1. Partial dependence

Partial Dependenceは機械学習モデルの予測結果を解釈するための手法の一つです。特に、複雑なモデルの出力を理解しやすくすることを目的としています。Partial Dependence Plot (PDP)では2001年にFriedmanさんによって紹介され、この手法に基づいてデータの特徴量（説明変数）の変化がモデルの出力（目的変数）にどのような影響を与えるかを可視化するための手法です。PDPは一つの特徴量を選択し、その特徴量の値を一定の範囲で変化させた時に、その特徴量がモデルの出力に与える影響をプロットします。他の特徴量は固定され、その他の要因が変化しないようにして、特徴量の影響を単独で調べることができます。モデルが学習した複雑な関係性を理解するのに役に立ちます。

モデル予測関数は
$$ \hat{\gamma }=\hat{f}(x_{1},x_{2},…,x_{m}) $$

Partial dependence functionの式は下記です。
$$ \hat{f_{k}}(x_{k})=E_{x_{\setminus k}}\left [ \hat{f}(x_{1},x_{2},…,x_{m}) \right ]=\int \hat{f}(x_{k},x_{\setminus k})p(x_{\setminus k})dx_{\setminus k} $$
\( x_{k} \)は入力変数で、\( x_{\setminus k} \)は他の予測変数の可能な値です。

上記の定義を下記の式で推定します。
$$ \bar{f_{k}}(x_{k})=\frac{1}{N}\sum_{i}^{N}\hat{f}(x_{k},x_{\setminus k, i}) $$

例として説明すると、下記の図のように、説明変数（Predictor）が一個ずつ変化され、それぞれの影響（Marginal impact）を測っていきます。

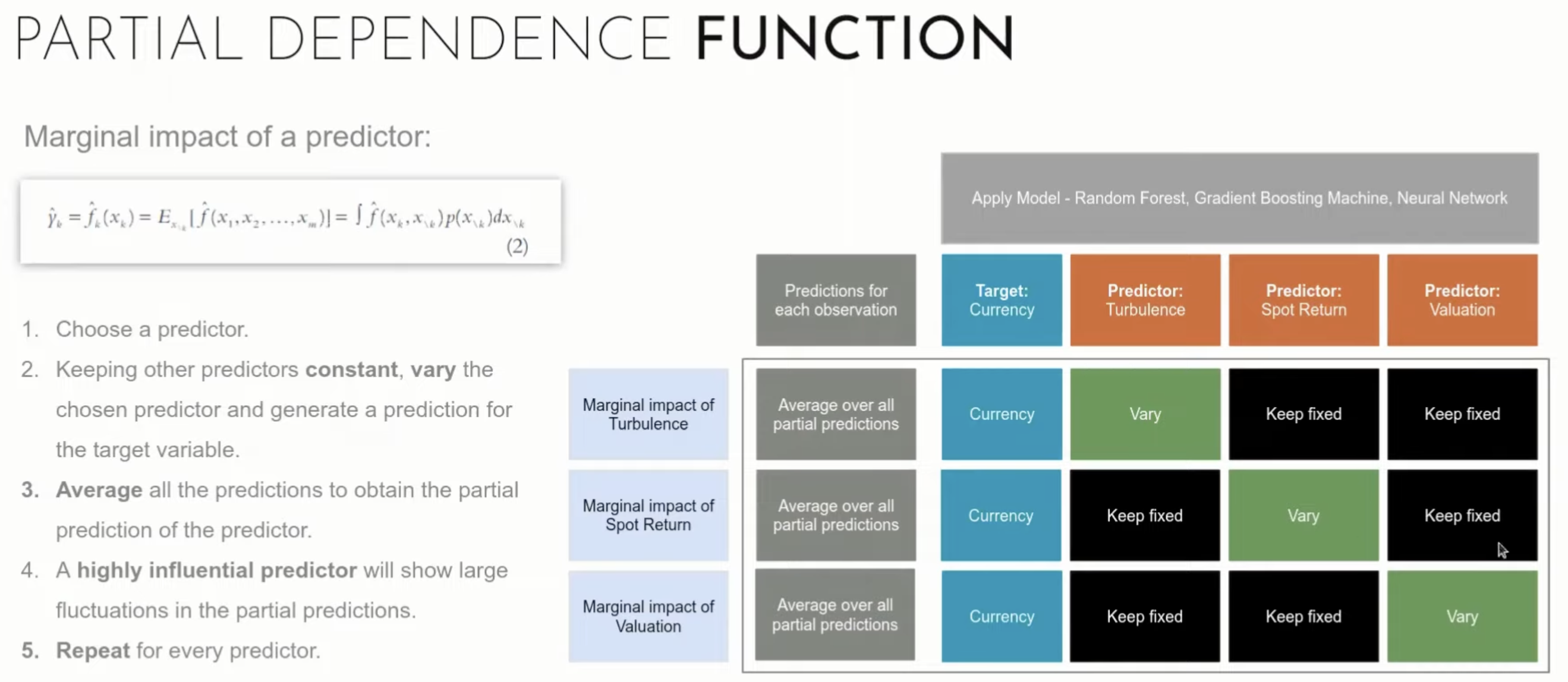
この図はModel Fingerprintsの紹介より引用

1.2. Linear prediction effect

Linear prediction effectはpartial dependence functionから、回帰線のベストフィット（最小二乗法）を求めることです。線形予測効果は平均値周りのmean absolute deviation(平均絶対偏差)と定義されています。

$$ Linear\ prediction\ effect\ (x_{k}) = \frac{1}{N}\sum_{i=1}^{N}abs\left ( \hat{l_{k}}\left [ x_{k,i} \right ]-\frac{1}{N}\sum_{j=1}^{N}\hat{f_{k}}\left [ x_{k,j} \right ] \right ) $$

この式では\(x_{k}\)の予測値に対して、\( \hat{l_{k}}\left [ x_{k,i} \right ] \)がpartial dependence functionの線形最小二乗法のフィット、\(x_{k,i}\)がデータセットの中で\(x_{k}\)のi番目の値を意味しています。

下記の図に対して、青線はPartial dependenceで、黒点線は予測の平均線、赤は線形でフィットされたものです。

この図はModel Fingerprintsの紹介より引用

個人的な想像を入れて説明しますが、これは線形の関係を説明したい意図だと思います。例えば、ある商品で、線形で取引高が増加するほど、プライス変化も上がっていく傾向を表すことが可能です。

1.3. Nonlinear prediction effect

Nonlinear prediction effectはLinear prediction effectにおける、一つの変数効果のmean absolute deviation(平均絶対偏差)と定義されています。

$$ Nonlinear\ prediction\ effect\ (x_{k}) = \frac{1}{N}\sum_{i=1}^{N}abs\left (\hat{f_{k}}\left [ x_{k,i} \right ]-\hat{l_{k}}\left [ x_{k,i} \right ]\right ) $$

下記の図に対して、青線はPartial dependenceで、赤は線形でフィットしたものです。

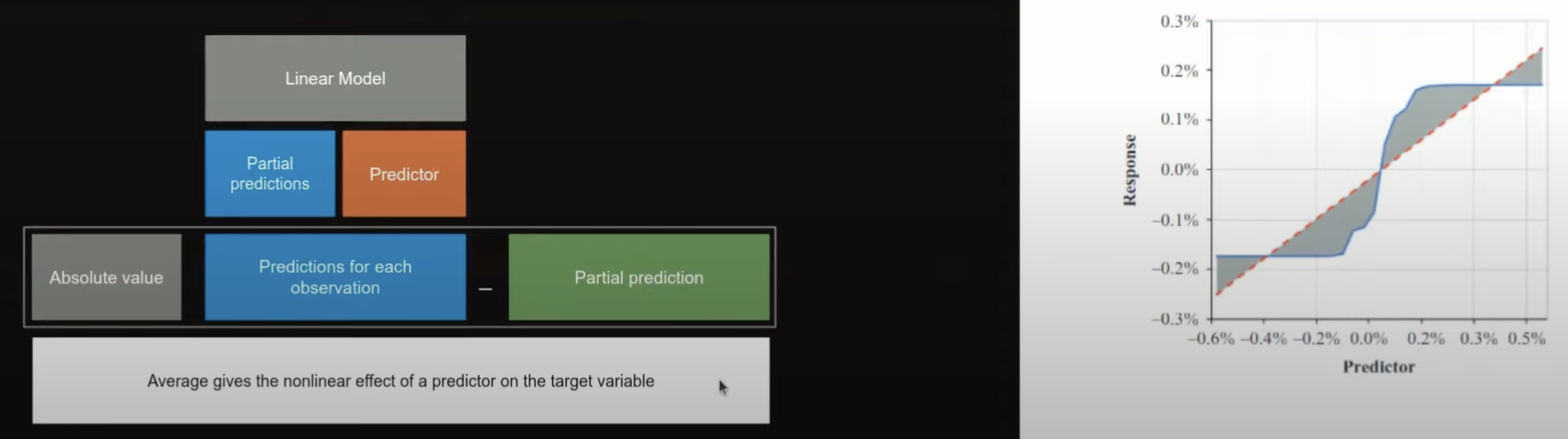
この図はModel Fingerprintsの紹介より引用

1.4. Pairwise interaction effect

Model Fingerprint論文が紹介したPairwise interaction effectはよく使われているFriedmanのH-staticticと似ています。H-statictic（H-統計量）は特徴量の相互作用(interaction)の強さを定量的に測定するための指標です。値は0-1の範囲で、0に近ければ特徴量間の相互作用が弱く、1に近ければ相互作用が強いことを示します。

Pairwise interaction effectはH-統計量と異なるポイントが二つあります。一つ目は、squared deviations(variance)がmean absolute deviationに変更され、異常なデータの敏感性が抑えられることです。二つ目は、denominator(normalization)を使わず、mean absolute deviationを直接利用することです。そうすることで、計算された値が解釈しやすくなるし、linearとNonlinear prediction effectsを比較できるようになります。

$$ H-statistic\ (H_{jk}^{2}) = \sum_{i=1}^{N}\left [\hat{f_{k,l}}\left ( x_{k,i} , x_{l,j}\right )-\hat{f_{k}} (x_{k,i} )-\hat{f_{l}} (x_{l,j} )\right ]^2 / \sum_{i=1}^{N}\hat{f_{k,l}}^{2} (x_{k,i} ) $$
$$ Pairwise\ interaction\ effect\ (x_{k}) = \frac{1}{N^{2}}\sum_{i=1}^{N}\sum_{j=1}^{N}abs\left [\hat{f_{k,l}}\left ( x_{k,i} , x_{l,j}\right )-\hat{f_{k}} (x_{k,i} )-\hat{f_{l}} (x_{l,j} )\right ] $$
\( \hat{f_{k}} (x_{k,i} \)と\( \hat{f_{l}} (x_{l,j} \)は入力変数と他の予測変数の可能な値です。

2. Model fingerprintsの使い方と応用例

2.1. 使い方

まず、まとめで少し繰り返しになりますが、Partial Prediction、Linear Effect、Nonlinear Effectの関係をグラフ化した図は下記です。LinearとNonlinear Effectsはグレー部分で表せます

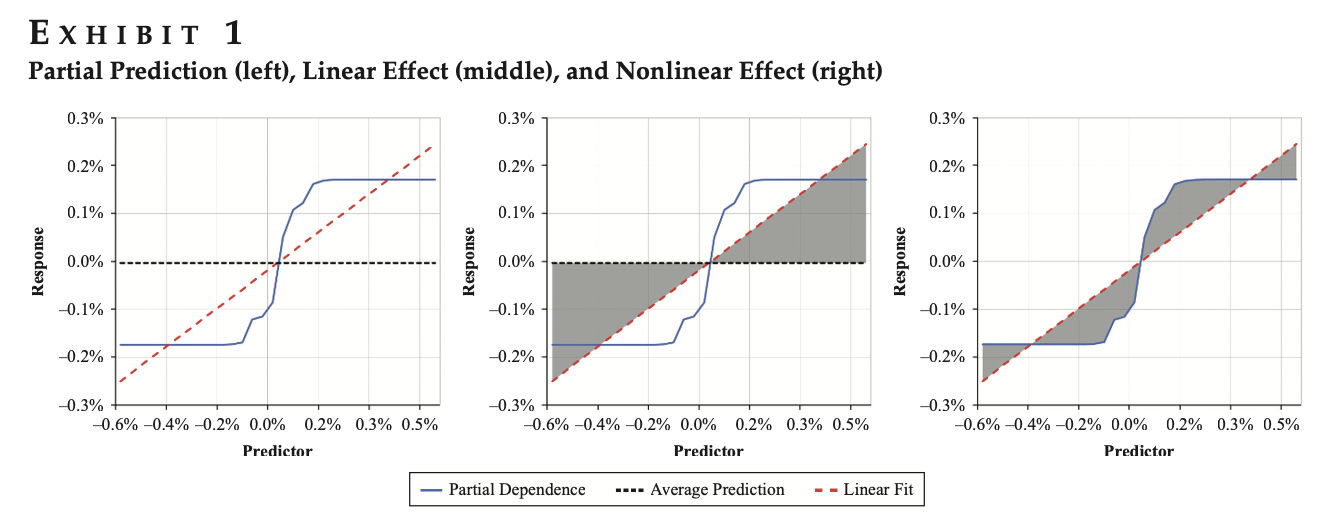
この図はModel Fingerprints論文より引用、左はPartial Prediction、真ん中はLinear Effect、右はNonlinear Effectです。

また、下記の図は2次元で孤立した一対の相互作用の例です。相互作用効果の総量は、この2つの次元で定義される表面下の体積に直感的に関係します（上記の斜線部分に相当します）。

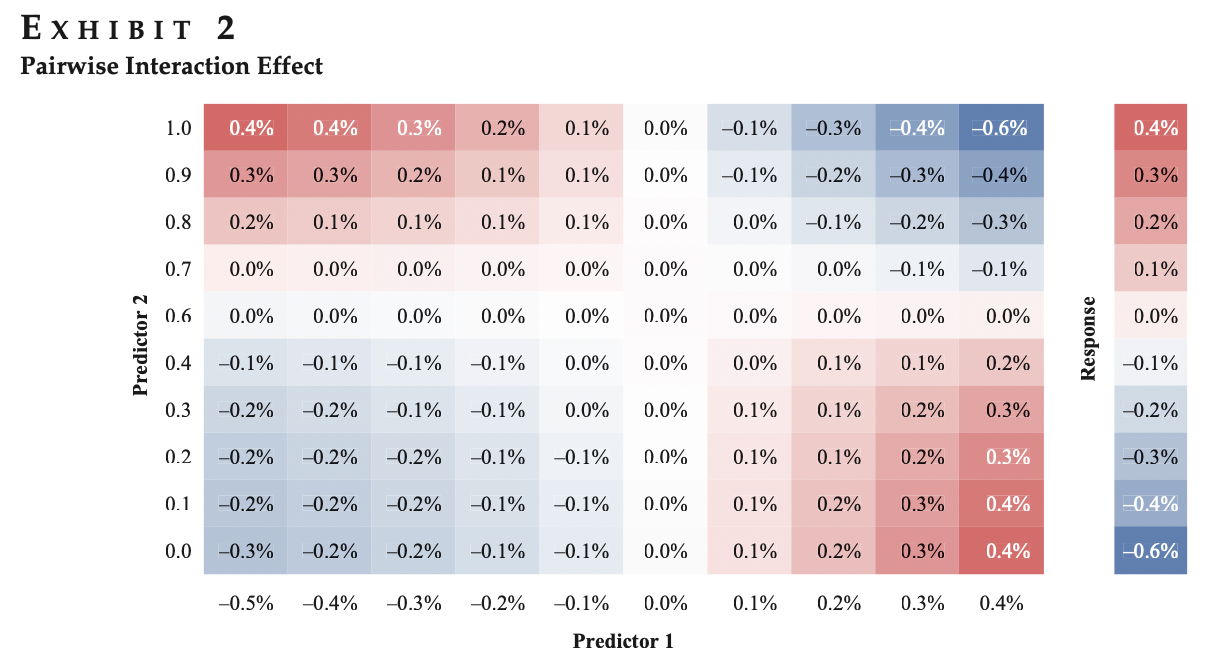
この図はModel Fingerprints論文より引用

著者はこれらの指標を使って、リターンのポートフォリオを比較するように使いました。

$$ \hat{\gamma}=\sum_{k=1}^{M}Linear\ Effect(x_{k})+\sum_{k=1}^{M}Nonlinear\ Effect(x_{k})+$$$$\sum_{{k,l}\in M, k\neq 1}^{}Pairwise\ interaction\ effect(x_{k},x_{l})+HigherOrder\ interaction\ effects $$

• 1. Linear (unconditional) performance effectは線形予測から計算されたポートフォリオのリターンの時系列に等しい
• 2. Pairwise interactions (conditional)performance effectは線形予測と一対の相互作用予測から計算されたポートフォリオのリターンの時系列に、ステップ 1 のリターンの時系列を差し引いたものに等しい
• 3. Nonlinear (sizing) performance effect:は線形、非線形、および一対の相互作用の組み合わせによる予測から計算されたポートフォリオのリターンの時系列に、ステップ 1 および 2 のリターンの時系列を引いたものに等しい
• 4. Higher-order interaction effect:は完全な予測モデルから計算されたポートフォリ オのリターンの時系列に、ステップ 1、2、3 のリターンの時系列を差し引いたものです。これは、予測モデルにおける一対の相互作用を超えて生じる高次の相互作用の影響を捉えるものです。

これらのパーフォーマンス効果を計算する順序は、一見奇妙に思えるかもしれませんが、重要な目的を果たすものでわざわざこうしたようです。interaction effectは、ある意味、nonlinear sizing effectよりも投資予測にとって根本的に重要なため、順番が2番目になっています。変数間の条件付き関係性を考慮に入れた相互作用は予測の方向性を劇的に変化させることができます。例えば、Bが低いときに、変数Aが正の予測因子とすると、Bが高いときは負の予測因子になります。さらに、変数Aは、その値が極端に高いや低いときに、その範囲の真ん中にあるときよりも強い予測因子（非線形効果）となります。この例では、Aのnonlinear performance effectを分離しようとすると、Bに対する条件性を考慮しなければ、非常に直感に反します、おそらく無意味な結果が得らるでしょう。nonlinear performance effectは、分離すると、Aの値が高くても低くても、より大きな予測値を意味します（U字型の曲線を想像してください）。Bとの組み合わせで初めて、これらの強い位置の半分が、完全なモデルの予測に入るとき、反対の符号を取ることがわかります。このような問題を完全に防ぐことはできないかもしれませんが、多くの一般的なモデルでは、パフォーマンス分解の非線形効果より先に相互作用効果を考慮することで、より有用な解釈分析が得られる可能性が高いと思われます。まとめると、非線形サイズ効果の前に条件付き関係を考慮することは合理的であると思われます。最後に、この問題は、前節の予測値の分解には影響しないことを指摘しておきます。なぜなら、その分析は、予測成分の強さに関係しており、その正負の方向には関係しないからです。

2.2. 応用例

著者が応用例として外貨投資を検証しました。この論文で検証された機械学習モデルは三つあり、①Random forest、②Gradient boosting machines、③Neural networksです。これらのモデルを実装し、リターンを比較したようです。結果としては、下記のポートフォリオ累積リターンによる、Neural NetworkとGradient Boosting MachineがRandom Forestより、優秀でした。

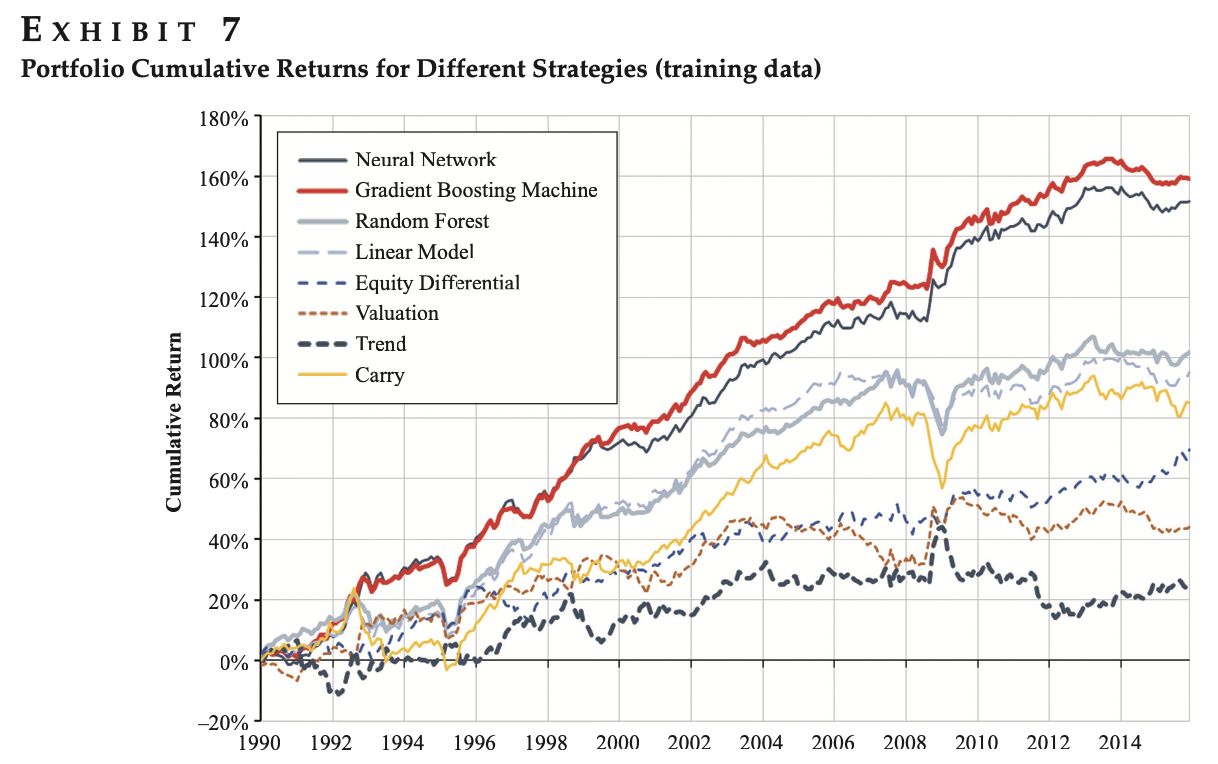
この図はModel Fingerprints論文より引用

なぜ、そうだったのかについて、Model Fingerprintを利用することで、説明が可能となると主張しました。下記のように、比較的に、Neural NetworkとGradient Boosting MachineがRandom ForestよりEffectの特徴を示すことでできたし、モデルにインパクトを与えた特徴量も解釈可能ということでした。

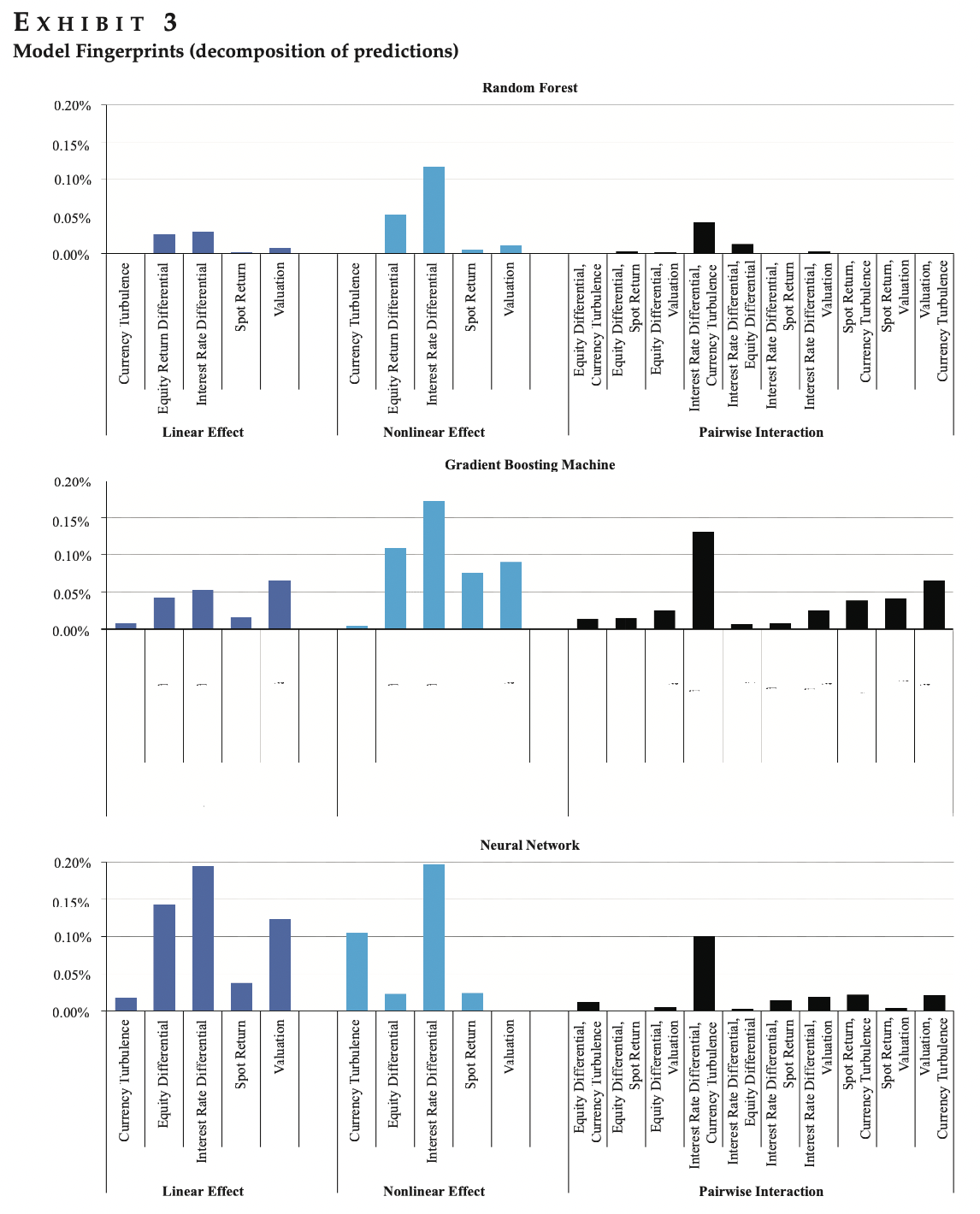
この図はModel Fingerprints論文より引用

3. まとめと考察

今回はModel Fingerprint手法を紹介しました。個人的に、この手法は投資のために、一般的な解釈可能な手法をベースにし、結構特殊でわざわざ金融的な考え方に合わせた印象でした。特に、有名なPartial dependenceとH -statisitcの計算式を変換したり、正規化を除外したりしていました。裏には投資のように金額的な考えが強いのかなと感じています。楽しく読ませて頂きましたが、本当に別のケースでも実用性的に使えるのかを興味がありいつか試してみたいと思ったりしました。

最後に

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。