2020.04.06
AutoMLによるFX予測してみた
こんにちは。次世代システム研究室のT.D.Qです。
前回は「TCNを用いてFX予測してみる」をテーマとしてブログを書きました。また、FX予測精度を向上するため、深層機械学習モデルのハイパーパラーメーターのチューニング技術及びツールを調査しました。予測精度の改善にある程度確認できましたが、特徴量選択は本当に良いか、データ準備から予測結果を得るまでより簡単な手法があるか悩みました。最近AIや機械学習ブームの中、AutoML(Automated Machine Learningの略)というワードをよく目にするようになりましたので、AutoMLで時系列データ予測に関する技術を調査しまして、時系列データから特徴量の選択やモデルの選択の処理も自動的に対応できそうなので今回の記事はAutoMLを用いてFX予測の検証を紹介したいと思います。
AutoMLについて
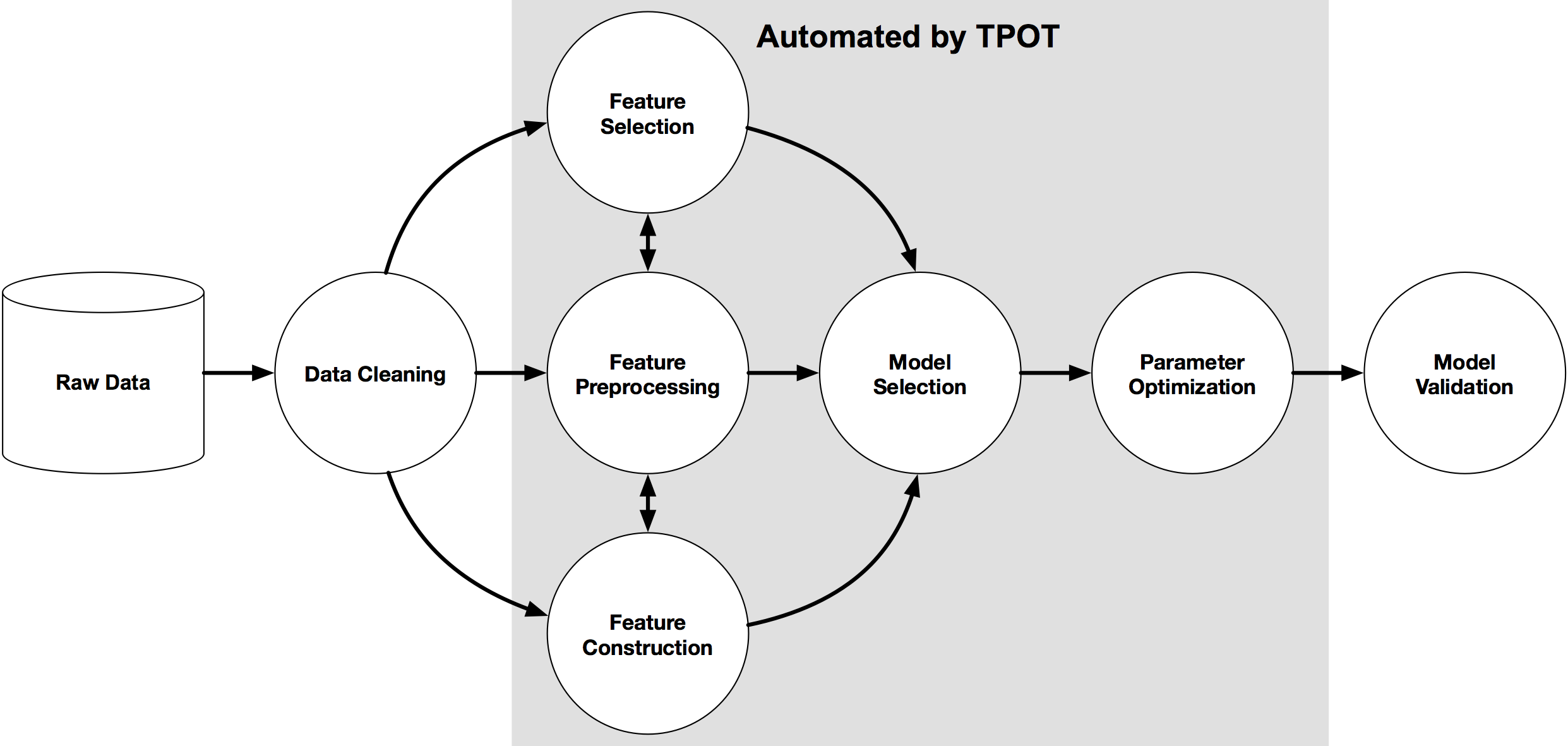
AutoMLとは、機械学習プロセスを自動化する技術であり、「機械学習の専門的な知識がなくても素早く、そして簡単に機械学習モデルを構築できる」というものです。機械学習のプロセスには、データ収集、データ前処理、モデルの選択、ハイパーパラメータのチューニング、モデルの評価など、いくつかの作業があるわけですが、AutoMLを利用すれば、このプロセスを自動化し、生産性の向上が期待できるため、煩雑な作業に時間がかかっていた機械学習のエンジニアからも注目されているのだと思います。
下記のイメージはAutoMLの概要で、AutoMLはCASH Problemのソリューションとしてモデル選択およびモデルのハイパーパラメータを探索するHPO(Hyper Parameter Optimization)問題から発展されていて、現在はニューラルネットワークの構造を自動で探索するNAS(Network Architecture Search)及び時系列データなどから高度な特徴量エンジニアリング技術を中心に研究されています。

今回はいくつかあるOSSフレームワークの中から、個人的に気になっているTfresh, Facebook Prophet,TPOT,H2Oを取り上げて実際に時系列データであるFX予測問題に使ってみたいと思います。
実行環境
今回もGPUクラウド by GMOの1GPUプランで下記のマシンで、nvidia-docker、Googleが提供するtensorflow:latest-gpu-jupyterイメージを使って機械学習の開発環境を構築してチューニングを行いました。
データ準備
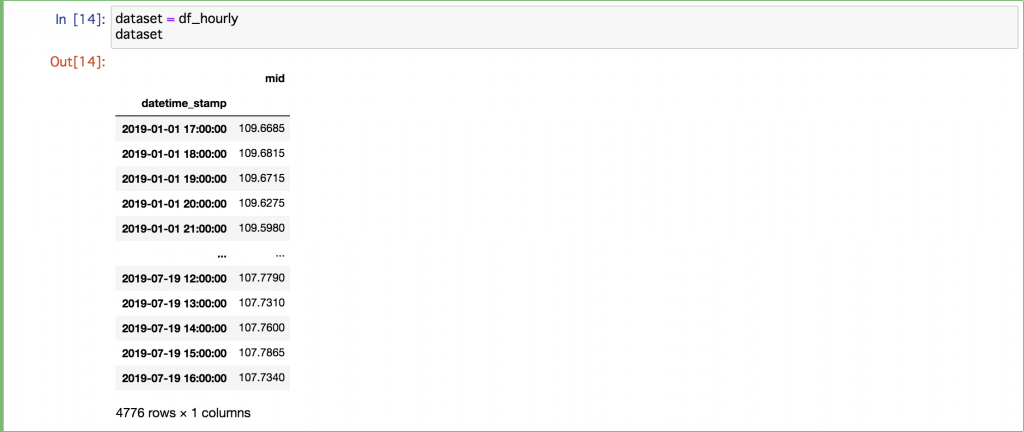
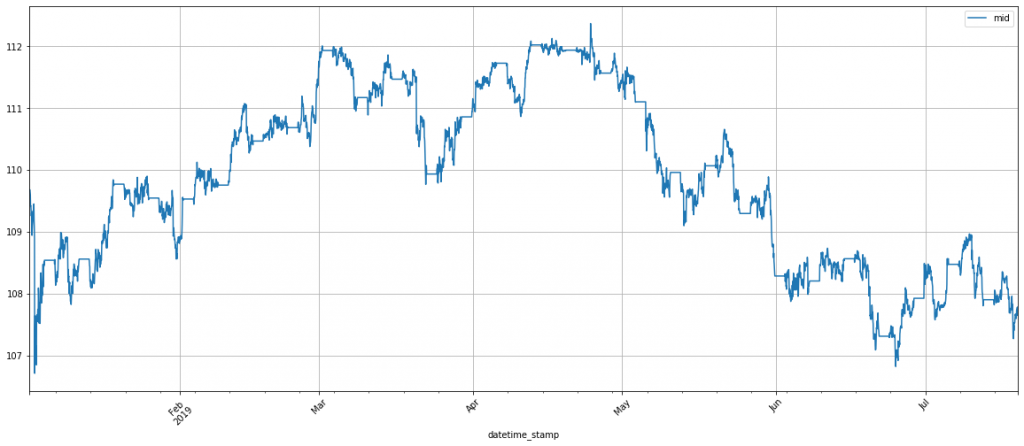
FXデータは前回のブログで準備したデータを再利用したいと思います。ドル円レートが2019年1月〜2019年7月分のTickデータとして入手し、欠損が多くてTickデータとしては使えなさそうですので、1時間足のデータにDownSamplingを行いました。そのデータからBid及びAskの平均値(Midプライス)を計算し、4776データポイントのdatasetとして使います。今回は、Midプライスを予測してみたいので目的変数はこのMidプライスですね。
TFreshを用いて特徴量エンジニアリングを行う
TFreshは時系列データから自動で特徴抽出するライブラリです。
まず、必要なパッケージをインポートします。
from tsfresh import select_features from tsfresh import extract_features from tsfresh.utilities.dataframe_functions import make_forecasting_frame from tsfresh.utilities.dataframe_functions import impute
MidプライスデータセットからTfreshの予測データフレームを作ります。
df_shift, y = make_forecasting_frame(dataset["mid"], kind="price", max_timeshift=25, rolling_direction=1)
あとは extract_features関数を利用するだけで、370特徴量を生成できます。
X = extract_features(df_shift, column_id="id", column_sort="time", column_value="value", impute_function=impute,
show_warnings=False)
X = X.loc[:, X.apply(pd.Series.nunique) != 1]
print(X.shape)
(4775, 370)
どんな特徴量が生成されたか確認して見ましょう。
X_train.columns ['value__abs_energy', 'value__absolute_sum_of_changes', 'value__agg_autocorrelation__f_agg_"mean"__maxlag_40', 'value__agg_autocorrelation__f_agg_"median"__maxlag_40', 'value__agg_autocorrelation__f_agg_"var"__maxlag_40', 'value__agg_linear_trend__f_agg_"max"__chunk_len_10__attr_"intercept"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_10__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_10__attr_"slope"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_10__attr_"stderr"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_5__attr_"intercept"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_5__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_5__attr_"slope"', 'value__agg_linear_trend__f_agg_"max"__chunk_len_5__attr_"stderr"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_10__attr_"intercept"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_10__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_10__attr_"slope"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_10__attr_"stderr"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_5__attr_"intercept"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_5__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_5__attr_"slope"', 'value__agg_linear_trend__f_agg_"mean"__chunk_len_5__attr_"stderr"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_10__attr_"intercept"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_10__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_10__attr_"slope"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_10__attr_"stderr"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_5__attr_"intercept"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_5__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_5__attr_"slope"', 'value__agg_linear_trend__f_agg_"min"__chunk_len_5__attr_"stderr"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_10__attr_"intercept"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_10__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_10__attr_"slope"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_10__attr_"stderr"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_5__attr_"intercept"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_5__attr_"rvalue"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_5__attr_"slope"', 'value__agg_linear_trend__f_agg_"var"__chunk_len_5__attr_"stderr"', 'value__approximate_entropy__m_2__r_0.1', 'value__approximate_entropy__m_2__r_0.3', 'value__approximate_entropy__m_2__r_0.5', 'value__approximate_entropy__m_2__r_0.7', 'value__approximate_entropy__m_2__r_0.9', 'value__ar_coefficient__k_10__coeff_0', 'value__ar_coefficient__k_10__coeff_1', 'value__ar_coefficient__k_10__coeff_2', 'value__ar_coefficient__k_10__coeff_3', 'value__ar_coefficient__k_10__coeff_4', 'value__augmented_dickey_fuller__autolag_"AIC"__attr_"pvalue"', 'value__augmented_dickey_fuller__autolag_"AIC"__attr_"teststat"', 'value__augmented_dickey_fuller__autolag_"AIC"__attr_"usedlag"', 'value__autocorrelation__lag_0', 'value__autocorrelation__lag_1', 'value__autocorrelation__lag_2', 'value__autocorrelation__lag_3', 'value__autocorrelation__lag_4', 'value__autocorrelation__lag_5', 'value__autocorrelation__lag_6', 'value__autocorrelation__lag_7', 'value__autocorrelation__lag_8', 'value__autocorrelation__lag_9', 'value__binned_entropy__max_bins_10', 'value__c3__lag_1', 'value__c3__lag_2', 'value__c3__lag_3', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.2__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.4__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.4__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.6__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.6__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.6__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.8__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.8__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.8__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_0.8__ql_0.6', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_1.0__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_1.0__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_1.0__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_1.0__ql_0.6', 'value__change_quantiles__f_agg_"mean"__isabs_False__qh_1.0__ql_0.8', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.2__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.4__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.4__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.6__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.6__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.6__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.8__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.8__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.8__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_0.8__ql_0.6', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_1.0__ql_0.0', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_1.0__ql_0.2', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_1.0__ql_0.4', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_1.0__ql_0.6', 'value__change_quantiles__f_agg_"mean"__isabs_True__qh_1.0__ql_0.8', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.2__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.4__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.4__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.6__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.6__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.6__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.8__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.8__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.8__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_0.8__ql_0.6', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_1.0__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_1.0__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_1.0__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_1.0__ql_0.6', 'value__change_quantiles__f_agg_"var"__isabs_False__qh_1.0__ql_0.8', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.2__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.4__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.4__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.6__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.6__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.6__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.8__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.8__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.8__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_0.8__ql_0.6', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_1.0__ql_0.0', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_1.0__ql_0.2', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_1.0__ql_0.4', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_1.0__ql_0.6', 'value__change_quantiles__f_agg_"var"__isabs_True__qh_1.0__ql_0.8', 'value__cid_ce__normalize_False', 'value__cid_ce__normalize_True', 'value__count_above_mean', 'value__count_below_mean', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_0__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_0__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_0__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_0__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_10__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_10__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_10__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_10__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_11__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_11__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_11__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_11__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_12__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_12__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_12__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_12__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_13__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_13__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_13__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_13__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_14__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_14__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_14__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_14__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_1__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_1__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_1__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_1__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_2__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_2__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_2__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_2__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_3__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_3__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_3__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_3__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_4__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_4__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_4__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_4__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_5__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_5__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_5__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_5__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_6__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_6__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_6__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_6__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_7__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_7__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_7__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_7__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_8__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_8__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_8__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_8__w_5', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_9__w_10', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_9__w_2', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_9__w_20', 'value__cwt_coefficients__widths_(2, 5, 10, 20)__coeff_9__w_5', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_0', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_1', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_2', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_3', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_4', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_5', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_6', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_7', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_8', 'value__energy_ratio_by_chunks__num_segments_10__segment_focus_9', 'value__fft_aggregated__aggtype_"centroid"', 'value__fft_aggregated__aggtype_"variance"', 'value__fft_coefficient__coeff_0__attr_"abs"', 'value__fft_coefficient__coeff_0__attr_"real"', 'value__fft_coefficient__coeff_10__attr_"abs"', 'value__fft_coefficient__coeff_10__attr_"angle"', 'value__fft_coefficient__coeff_10__attr_"imag"', 'value__fft_coefficient__coeff_10__attr_"real"', 'value__fft_coefficient__coeff_11__attr_"abs"', 'value__fft_coefficient__coeff_11__attr_"angle"', 'value__fft_coefficient__coeff_11__attr_"imag"', 'value__fft_coefficient__coeff_11__attr_"real"', 'value__fft_coefficient__coeff_12__attr_"abs"', 'value__fft_coefficient__coeff_12__attr_"angle"', 'value__fft_coefficient__coeff_12__attr_"imag"', 'value__fft_coefficient__coeff_12__attr_"real"', 'value__fft_coefficient__coeff_1__attr_"abs"', 'value__fft_coefficient__coeff_1__attr_"angle"', 'value__fft_coefficient__coeff_1__attr_"imag"', 'value__fft_coefficient__coeff_1__attr_"real"', 'value__fft_coefficient__coeff_2__attr_"abs"', 'value__fft_coefficient__coeff_2__attr_"angle"', 'value__fft_coefficient__coeff_2__attr_"imag"', 'value__fft_coefficient__coeff_2__attr_"real"', 'value__fft_coefficient__coeff_3__attr_"abs"', 'value__fft_coefficient__coeff_3__attr_"angle"', 'value__fft_coefficient__coeff_3__attr_"imag"', 'value__fft_coefficient__coeff_3__attr_"real"', 'value__fft_coefficient__coeff_4__attr_"abs"', 'value__fft_coefficient__coeff_4__attr_"angle"', 'value__fft_coefficient__coeff_4__attr_"imag"', 'value__fft_coefficient__coeff_4__attr_"real"', 'value__fft_coefficient__coeff_5__attr_"abs"', 'value__fft_coefficient__coeff_5__attr_"angle"', 'value__fft_coefficient__coeff_5__attr_"imag"', 'value__fft_coefficient__coeff_5__attr_"real"', 'value__fft_coefficient__coeff_6__attr_"abs"', 'value__fft_coefficient__coeff_6__attr_"angle"', 'value__fft_coefficient__coeff_6__attr_"imag"', 'value__fft_coefficient__coeff_6__attr_"real"', 'value__fft_coefficient__coeff_7__attr_"abs"', 'value__fft_coefficient__coeff_7__attr_"angle"', 'value__fft_coefficient__coeff_7__attr_"imag"', 'value__fft_coefficient__coeff_7__attr_"real"', 'value__fft_coefficient__coeff_8__attr_"abs"', 'value__fft_coefficient__coeff_8__attr_"angle"', 'value__fft_coefficient__coeff_8__attr_"imag"', 'value__fft_coefficient__coeff_8__attr_"real"', 'value__fft_coefficient__coeff_9__attr_"abs"', 'value__fft_coefficient__coeff_9__attr_"angle"', 'value__fft_coefficient__coeff_9__attr_"imag"', 'value__fft_coefficient__coeff_9__attr_"real"', 'value__first_location_of_maximum', 'value__first_location_of_minimum', 'value__friedrich_coefficients__m_3__r_30__coeff_0', 'value__friedrich_coefficients__m_3__r_30__coeff_1', 'value__friedrich_coefficients__m_3__r_30__coeff_2', 'value__friedrich_coefficients__m_3__r_30__coeff_3', 'value__has_duplicate', 'value__has_duplicate_max', 'value__has_duplicate_min', 'value__index_mass_quantile__q_0.1', 'value__index_mass_quantile__q_0.2', 'value__index_mass_quantile__q_0.3', 'value__index_mass_quantile__q_0.4', 'value__index_mass_quantile__q_0.6', 'value__index_mass_quantile__q_0.7', 'value__index_mass_quantile__q_0.8', 'value__index_mass_quantile__q_0.9', 'value__kurtosis', 'value__large_standard_deviation__r_0.05', 'value__large_standard_deviation__r_0.1', 'value__large_standard_deviation__r_0.15000000000000002', 'value__large_standard_deviation__r_0.2', 'value__large_standard_deviation__r_0.25', 'value__large_standard_deviation__r_0.30000000000000004', 'value__large_standard_deviation__r_0.35000000000000003', 'value__large_standard_deviation__r_0.4', 'value__large_standard_deviation__r_0.45', 'value__large_standard_deviation__r_0.5', 'value__large_standard_deviation__r_0.55', 'value__large_standard_deviation__r_0.6000000000000001', 'value__large_standard_deviation__r_0.65', 'value__large_standard_deviation__r_0.7000000000000001', 'value__large_standard_deviation__r_0.75', 'value__large_standard_deviation__r_0.8', 'value__large_standard_deviation__r_0.8500000000000001', 'value__large_standard_deviation__r_0.9', 'value__large_standard_deviation__r_0.9500000000000001', 'value__last_location_of_maximum', 'value__last_location_of_minimum', 'value__length', 'value__linear_trend__attr_"intercept"', 'value__linear_trend__attr_"pvalue"', 'value__linear_trend__attr_"rvalue"', 'value__linear_trend__attr_"slope"', 'value__linear_trend__attr_"stderr"', 'value__longest_strike_above_mean', 'value__longest_strike_below_mean', 'value__max_langevin_fixed_point__m_3__r_30', 'value__maximum', 'value__mean', 'value__mean_abs_change', 'value__mean_change', 'value__mean_second_derivative_central', 'value__median', 'value__minimum', 'value__number_cwt_peaks__n_1', 'value__number_cwt_peaks__n_5', 'value__number_peaks__n_1', 'value__number_peaks__n_10', 'value__number_peaks__n_3', 'value__number_peaks__n_5', 'value__partial_autocorrelation__lag_1', 'value__partial_autocorrelation__lag_2', 'value__partial_autocorrelation__lag_3', 'value__partial_autocorrelation__lag_4', 'value__partial_autocorrelation__lag_5', 'value__partial_autocorrelation__lag_6', 'value__partial_autocorrelation__lag_7', 'value__partial_autocorrelation__lag_8', 'value__partial_autocorrelation__lag_9', 'value__percentage_of_reoccurring_datapoints_to_all_datapoints', 'value__percentage_of_reoccurring_values_to_all_values', 'value__quantile__q_0.1', 'value__quantile__q_0.2', 'value__quantile__q_0.3', 'value__quantile__q_0.4', 'value__quantile__q_0.6', 'value__quantile__q_0.7', 'value__quantile__q_0.8', 'value__quantile__q_0.9', 'value__range_count__max_1000000000000.0__min_0', 'value__ratio_beyond_r_sigma__r_0.5', 'value__ratio_beyond_r_sigma__r_1', 'value__ratio_beyond_r_sigma__r_1.5', 'value__ratio_beyond_r_sigma__r_2', 'value__ratio_beyond_r_sigma__r_2.5', 'value__ratio_beyond_r_sigma__r_3', 'value__ratio_value_number_to_time_series_length', 'value__sample_entropy', 'value__skewness', 'value__spkt_welch_density__coeff_2', 'value__spkt_welch_density__coeff_5', 'value__spkt_welch_density__coeff_8', 'value__standard_deviation', 'value__sum_of_reoccurring_data_points', 'value__sum_of_reoccurring_values', 'value__sum_values', 'value__symmetry_looking__r_0.05', 'value__symmetry_looking__r_0.1', 'value__symmetry_looking__r_0.15000000000000002', 'value__symmetry_looking__r_0.2', 'value__symmetry_looking__r_0.25', 'value__symmetry_looking__r_0.30000000000000004', 'value__symmetry_looking__r_0.35000000000000003', 'value__symmetry_looking__r_0.4', 'value__symmetry_looking__r_0.45', 'value__symmetry_looking__r_0.5', 'value__symmetry_looking__r_0.55', 'value__symmetry_looking__r_0.6000000000000001', 'value__symmetry_looking__r_0.65', 'value__symmetry_looking__r_0.7000000000000001', 'value__symmetry_looking__r_0.75', 'value__symmetry_looking__r_0.8', 'value__symmetry_looking__r_0.8500000000000001', 'value__symmetry_looking__r_0.9', 'value__symmetry_looking__r_0.9500000000000001', 'value__time_reversal_asymmetry_statistic__lag_1', 'value__time_reversal_asymmetry_statistic__lag_2', 'value__time_reversal_asymmetry_statistic__lag_3', 'value__variance', 'feature_last_value']
以上、TFreshがMidプライスの時系列データセットから時系列の370特徴量を生成してもらいました。次にこのデータを使ってAutoMLフレームワークに予測してみましょう。
予測モデル構築
Baselineを作る
上記のデータを用いて「Auto ARIMAX」というモデルに適用してBaselineを作りました。今回の記事はAutoMLに集中して紹介したいので、Auto ARIMAXは具体的に紹介しませんが、今回の時系列データを使って予測結果のMAEが0.04080697540619879でまあまあ良い感じです。
※平均絶対誤差(MAE:Mean Absolute Error)が誤差の絶対値を平均したものです。MAEが0に近いほど見積もられる予測誤差が小さい、すなわち予測精度が高いことを表します。今回の記事はこの指標を使って予測モデルの制度を評価します。
Facebook Prophet
Facebook Prophetが時系列データ専用のフェイスブックが作った機械学習ライブラリです。
Facebookの論文から見ると y(t)を時刻tにおける予測値としたモデル式は以下の通りです。
y(t)=g(t)+s(t)+h(t)+ϵ(t)
g(t)がトレンド成分、s(t)が季節成分、h(t)が祝日などのイレギュラーな日程における効果成分、ϵ(t)が誤差項です。 この式の形は一般化加法モデル(Generalized Additive Model)と似た形となっています。
今回はバージョンfbprophet==0.2.1をpythonで試していきます。
まず、Prophetなど必要なパッケージをインポートし、上記作成したデータセットからtrain, testデータセットを作ります。
Prophetで時系列解析を行うためには,以下のカラムを持つpandas.DataFrameを生成する必要があるので要注意です。
・ds:日付カラム
・y:予測対象カラム
from tqdm import tqdm
from fbprophet import Prophet
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.9, test_size=0.1, shuffle=False)
y_train_wi = y_train.reset_index()
y_test_wi = y_test.reset_index()
X_train_wi = X_train.reset_index()
X_test_wi = X_test.reset_index()
train_df = pd.concat([y_train_wi, X_train_wi], axis = 1).rename(columns = {'datetime_stamp': 'ds', 'value': 'y'})
test_df = pd.concat([y_test_wi, X_test_wi], axis = 1).rename(columns = {'datetime_stamp': 'ds', 'value': 'y'})
train_df = train_df.drop(['id'], axis=1)
test_df = test_df.drop(['id'], axis=1)
Prophetの予測モデルを生成してトレーニングデータで学習を行います。学習したモデルfp_modelを使い、テストデータフレームのFXプライスを予測しましょう。
fp_model = Prophet()
for feature in tqdm(X_train.columns):
fp_model.add_regressor(feature)
fp_model.fit(train_df)
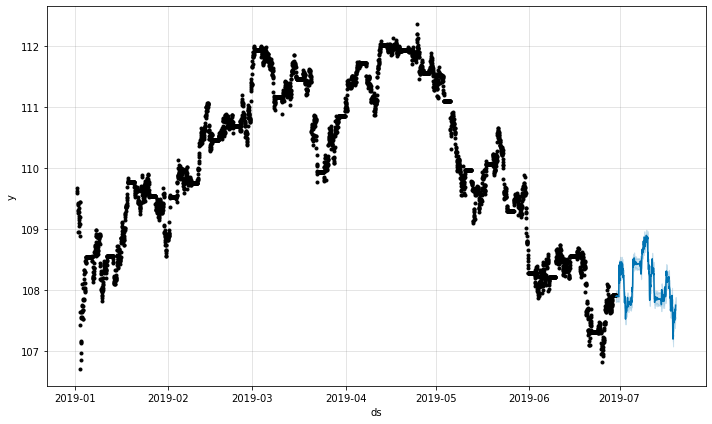
fp_forecase = fp_model.predict(test_df)
fp_model.plot(fp_forecase)
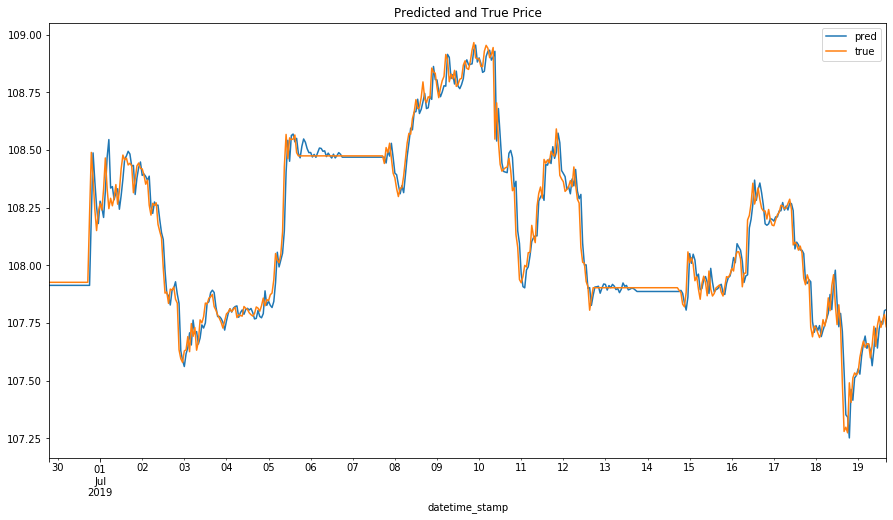
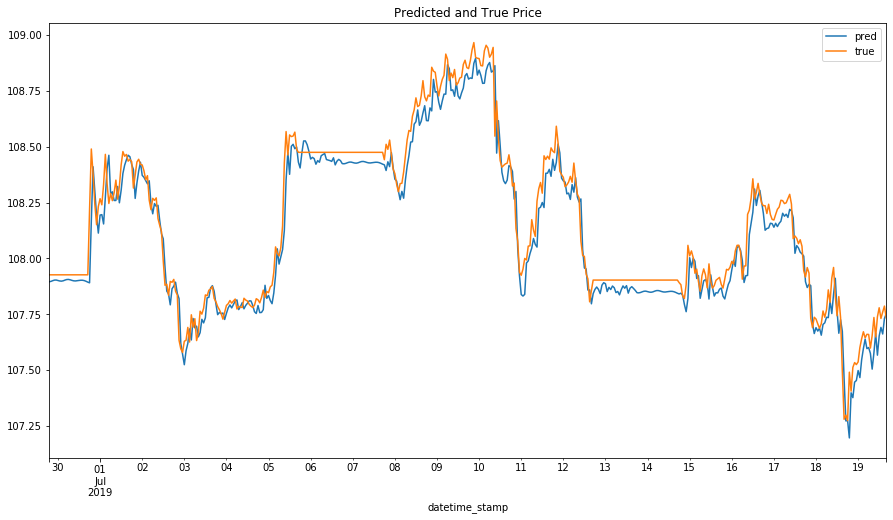
予測結果を可視化して確認しましょう。
y_pred = pd.Series(data=fp_forecase.yhat.values, index=y_test.index)
ys = pd.concat([y_pred, y_test], axis = 1).rename(columns = {0: 'pred', 'value': 'true'})
# Convert index to a datetime
ys.index = pd.to_datetime(ys.index)
ys[["pred","true"]].plot(figsize=(15, 8))
plt.title('Predicted and True Price')
plt.show()
print("MAE of Facebook Prophet: \t{}".format(np.mean(np.abs(y_pred - y_test)[100:])))
MAE of Facebook Prophet: 0.06151289468035056
予測精度は悪くないですが、Baselineより下になってしまいました。予測精度を向上するためまたチューニングする必要があるかもしれませんね。
TPOT
TPOTは、Tree-Based Pipeline Optimization Toolの略で遺伝的プログラミングを使用して機械学習パイプラインを最適化するPython AutoMLフレームワークです。TPOTは分類問題はもちろん、回帰問題のためにパイプラインを最適化することができます。
times=[] scores=[] winning_pipelines = [] from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, test_size=0.25, shuffle=False)
TPOTの回帰モデルを生成して使います。遺伝的アルゴリズムならではの「世代」及び「個体数」引数を設定する必要がありますね。
・generations:世代。パイプライン最適化の繰り返し回数です
・population size:個体群
from tqdm import tqdm
from tpot import TPOTRegressor
tpot = TPOTRegressor(
generations=15,
population_size=50,
random_state=25,
early_stop=20,
verbosity=2,
n_jobs=-1)
学習を行い、予測制度が高いというエリートモデルを保存します。
import timeit
# Run 3 iterations
for i in tqdm(range(3)):
start_time=timeit.default_timer()
tpot.fit(X_train, y_train)
elapsed = timeit.default_timer() - start_time
times.append(elapsed)
winning_pipelines.append(tpot.fitted_pipeline_)
scores.append(tpot.score(X_test, y_test))
tpot.export('tpot_mid_price_prediction.py')
TPOTのscore関数でエリートモデルの予測制度を確認してみます。
print(tpot.score(X_test, y_test))
-0.004463602261859715
エリートモデルの詳細を確認しましょう。
winning_pipelines
[Pipeline(memory=None,
steps=[('zerocount', ZeroCount()),
('selectfrommodel',
SelectFromModel(
estimator=ExtraTreesRegressor(
bootstrap=False,
ccp_alpha=0.0,
criterion='mse',
max_depth=None,
max_features=0.8,
max_leaf_nodes=None,
max_samples=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators=100,
n_jobs=None,
oob_score=False,
random_state=25,
verbose=0,
warm_start=False),
max_features=None, norm_order=1, prefit=False,
threshold=0.1)),
('lassolarscv',
LassoLarsCV(copy_X=True, cv=None,
eps=2.220446049250313e-16,
fit_intercept=True, max_iter=500,
max_n_alphas=1000,
n_jobs=None, normalize=True,
positive=False, precompute='auto',
verbose=False))],
verbose=False), Pipeline(memory=None,
steps=[('selectpercentile-1',
SelectPercentile(
percentile=21,
score_func=<function f_regression at 0x7fd6d7cb9b70>)),
('selectpercentile-2',
SelectPercentile(
percentile=73,
score_func=<function f_regression at 0x7fd6d7cb9b70>)),
('lassolarscv',
LassoLarsCV(copy_X=True, cv=None,
eps=2.220446049250313e-16,
fit_intercept=True, max_iter=500,
max_n_alphas=1000,
n_jobs=None, normalize=True,
positive=False, precompute='auto',
verbose=False))],
verbose=False), Pipeline(memory=None,
steps=[('zerocount', ZeroCount()),
('selectfrommodel',
SelectFromModel(
estimator=ExtraTreesRegressor(
bootstrap=False,
ccp_alpha=0.0,
criterion='mse',
max_depth=None,
max_features=0.8,
max_leaf_nodes=None,
max_samples=None,
min_impurity_decrease=0.0,
min_impurity_split=None,
min_samples_leaf=1,
min_samples_split=2,
min_weight_fraction_leaf=0.0,
n_estimators=100,
n_jobs=None,
oob_score=False,
random_state=25,
verbose=0,
warm_start=False),
max_features=None, norm_order=1, prefit=False,
threshold=0.1)),
('lassolarscv',
LassoLarsCV(copy_X=True, cv=None,
eps=2.220446049250313e-16,
fit_intercept=True, max_iter=500,
max_n_alphas=1000,
n_jobs=None, normalize=True,
positive=False, precompute='auto',
verbose=False))],
verbose=False)]
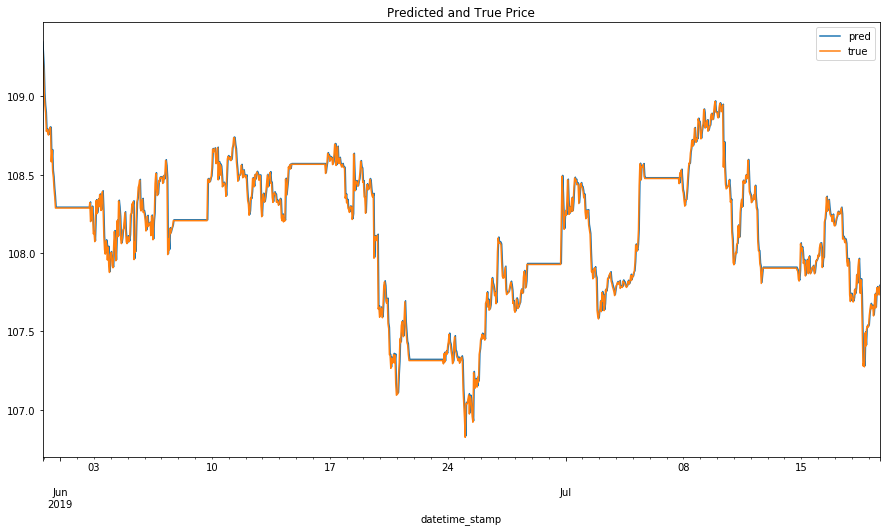
予測結果を可視化しましょう。
y_pred = tpot.predict(X_test)
y_pred = pd.Series(data=y_pred, index=y_test.index)
# Dataframe of predictions and true values
ys = pd.concat([y_pred, y_test], axis = 1).rename(columns = {0: 'pred', 'value': 'true'})
# Convert index to a datetime
ys.index = pd.to_datetime(ys.index)
ys.plot(figsize=(15, 8))
plt.title('Predicted and True Price')
plt.show()
print("MAE TPOT: \t{}".format(np.mean(np.abs(ys['pred'] - ys['true']))))
MAE TPOT: 0.040134344215542454
なるほど。今回はTPOTの予測制度がBaselineの制度より少し上ですね。
H2O AutoML
H2O AutoMLはH20.aiのオープンソース分散型インメモリ機械学習プラットフォームです。H2OのAutoMLは、ユーザーが指定した時間制限内で多くのモデルの自動トレーニングやチューニングを含む機械学習ワークフローの自動化に使用できます。
H2O AutoMLを使ってFX予測をしましょう。まず、上記のMidプライスデータセットからtrain, eval, testデータフレームを作成しておきます。
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, test_size=0.2, shuffle=False)
X_train, X_val, y_train, y_val = train_test_split(X, y, train_size=0.8, test_size=0.2, shuffle=False)
train_df = pd.concat([X_train, y_train], axis = 1).rename(columns = { 'value': 'mid_price'})
eval_df = pd.concat([X_val, y_val], axis = 1).rename(columns = { 'value': 'mid_price'})
test_df = pd.concat([X_test, y_test], axis = 1).rename(columns = {'value': 'mid_price'})
次に、学習・予測を行うため、H2Oサーバを起動します。
from tqdm import tqdm import h2o from h2o.automl import H2OAutoML h2o.init(nthreads=-1)
H2Oサーバが正常に起動すれば下記のログが出てきますね。
次に、学習と検証データフレームをH2Oで使えるように変換しないといけないので変換しておきます。
#Convert pandas DataFrame to H2O dataframe hf_train = h2o.H2OFrame(train_df) hf_eval = h2o.H2OFrame(eval_df) hf_test = h2o.H2OFrame(test_df) X_Labels = hf_train.columns y_label = 'mid_price' X_Labels.remove(y_label)
ここまで準備できましたので、H2OAutoMLのインスタンスを生成して学習を行いましょう。
#AutoMLを最大6時間実行するための設定
aml = H2OAutoML(max_runtime_secs=21600)
#モデルの学習を行う。予測対象変数 (y) と予測に用いる変数 (x)にTrainデータセットを設定し、
#検証するためのデータセットも設定します。
aml.train(x=X_Labels, y=y_label,
training_frame=hf_train,
validation_frame=hf_eval,
leaderboard_frame=hf_test
)

作成したモデルのLeader Boardが以下のように表示されます。StackingのアンサンブルモデルやGLM(一般化線形モデル)が良いらしいですね。
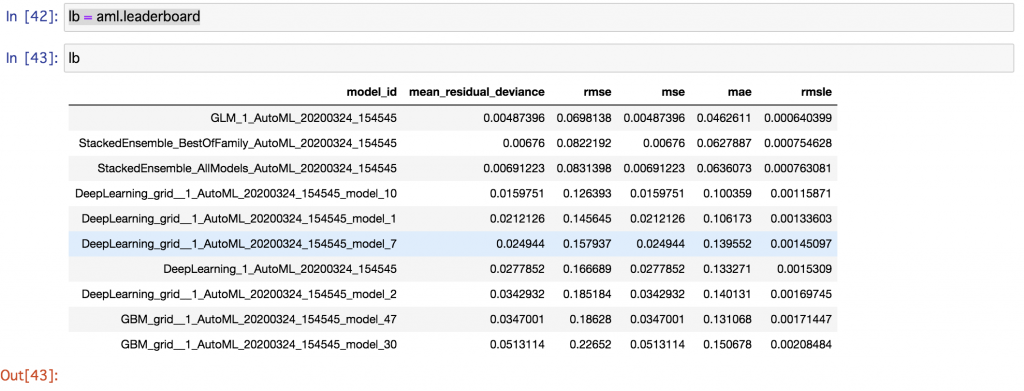
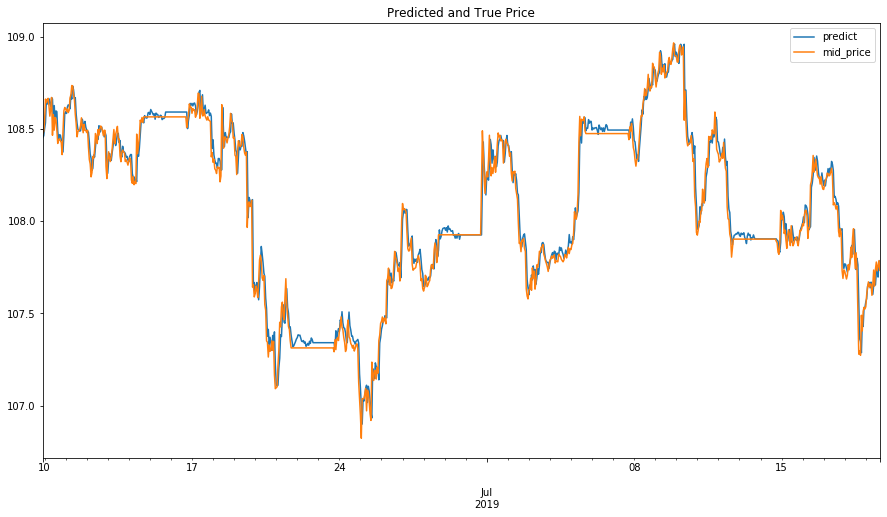
学習が終わって、一番制度が良いモデル(leader)を得たのでこのモデルを使って予測を検証しましょう。
ld_predict = aml.leader.predict(hf_test)
y_pred = ld_predict.as_data_frame()
y_pred.index = pd.to_datetime(test_df.index)
# Dataframe of predictions and true values
ys = pd.concat([y_pred, test_df['mid_price']], axis = 1)
ys.plot(figsize=(15, 8))
plt.title('Predicted and True Price')
plt.show()
ys['diff'] = ys['predict'] - ys['mid_price']
print("MAE H2O: \t{}".format(np.mean(np.abs(ys['diff'].values ))))
h2o.cluster().shutdown()
MAE H2O: 0.04626089659685803
結果まとめ
今回は、TFreshを使って時系列データの特徴量を自動的に作って、AutoMLのフレームワークに適用してFXのMidプライス予測をしてみました。使ったAutoMLフレームワークによってトレーニング時間に大きな差がある一方、MAE値にはBaselineよりそれほど大きな差は出ませんでしたが、もう少しチューニングして精度改善できることを期待できそうです。また、ほとんど設定の必要がなく、データを入れてすぐにはじめることができるので、統計・機械学習が分からない人でも実装ができると思いますが、データから結果を得るまではほとんどブラックボックスなので、ある程度機械学習の知識がある方が使わないと誤った使い方をしてしまいそうです。今回のFX予測結果から見ると本番で求める高精度の予測はまだ厳しいと思いますが、PoCで試しにやるならAutoMLは簡単で高い精度が出るので良いかと思いました。
最後に
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD