2020.04.07
遺伝的アルゴリズムで遊んでみる
こんにちは。次世代システム研究室のJK(男)です。今回は遺伝的アルゴリズム(GA)について書きます。
GAは進化計算(生物の進化のメカニズムにヒントを得て、データ構造を変形していくアルゴリズム)の一手法です。コンセプトは単純なので昔から研究されています。しかし昨今のディープラーニングブームの中で、進化計算も再び見直しがされているようです(たとえばこれ)。今回はGAをニューラルネットワークに適用してその特性を少し見てみたいと思います。なお今回のブログの内容はこちらの書籍の6章を基に書いています。
1.遺伝的アルゴリズムのコンセプト
GAは生物の進化をヒントに作られています。生物の進化といえばダーウィンの自然淘汰説が基本ですね。Wikipediaで調べてみると「厳しい自然環境が、生物に無目的に起きる変異(突然変異)を選別し、進化に方向性を与えるという説」だそうです。要点をまとめると「進化 = 変異→選択-by-環境」ですかね。上記の定義は言外に二つのことを前提にしています。一つは進化は個体でなく集団に適用されること(「選別」が起きるためには集団であることが前提)。もう一つは(変異→選択)は何度も繰り返されること(「世代」が進むにつれ進化する)。
上記のコンセプトをデータ構造の変形に適用したのがGAです。ここでは説明を簡単にするため、強化学習(たとえば以前のブログ参照)と同様の問題設定を考えます。つまり環境があり、その環境の下で行動するエージェントがいます。エージェントは得られる「報酬」が多くなるような行動ができるように「学習」するとします。ここで報酬→適応度、学習→進化と読み替えればGAを適用できます。「エージェントの行動」は「遺伝情報」で決まるように設定して、GAは世代ごとに遺伝情報を変更していきます。以下のようなループ構造で世代が進むごとに「適応度」が上がっていく、ということですね。
population_size(集団の個体数;ハイパーパラメータ)の設定 初期集団(第一世代)の設定 世代数 = 1 While True: 現世代分の適応度計算 = 各個体の(環境下での)適応度を計算 for _ in range(population_size): 適応度に応じて、集団から個体を選択 次世代の個体を作成 = 選択した個体に対して突然変異etcさせる 世代数 += 1
混乱するかもですが、環境上に集団エージェントを同時に置いてるわけではありません(そういう手もあるでしょうが)。各個体毎に別々に適応度は計算してます。並列で計算も可能です。
2.実験の概要
具体例があった方がわかりやすいと思うので、今回の実験に即してもう少し詳しくアルゴリズムを見ていきます。細かいことを言えば色々な手法があると思いますが、ここではテキストに書いてあるスタンダードと思われる手法を説明します。
実験の設定は、1エージェントが2次元上のマップで動き回るようになっています(動画1参照)。マップ上に餌が分布しており(マップ上の黄色い部分が餌が多くあり、青いところが餌がない)、エージェントは餌の位置に移動することでその餌を食べることができます。エージェントは1試行毎に固定したステップ(=時間)だけ行動でき、行動が終わった後の餌の量を「適応度」とします。つまり餌をたくさん食べたエージェントが適応度の高いエージェントです。
動画1. 実験の概要の説明用
今回の実験ではエージェントをニューラルネット(NN)を使って行動させます。つまり環境からの情報をインプットとし、エージェントの行動をアウトプットと定義したNNを作成します。インプットはエージェントの接する周囲の餌の情報と直前のエージェントの状態です。インプットに対する行動はNNの重みで決まるので、ここでは重み=遺伝情報としてエージェントを進化させます。重みを一次元のデータ(配列)として、これに対して変形を加えていきます。具体的には「1.複製、2.重みの一部の値をランダムに変更(突然変異)、3.2つのエージェントを混ぜる(交叉)」があります(図1参照)。
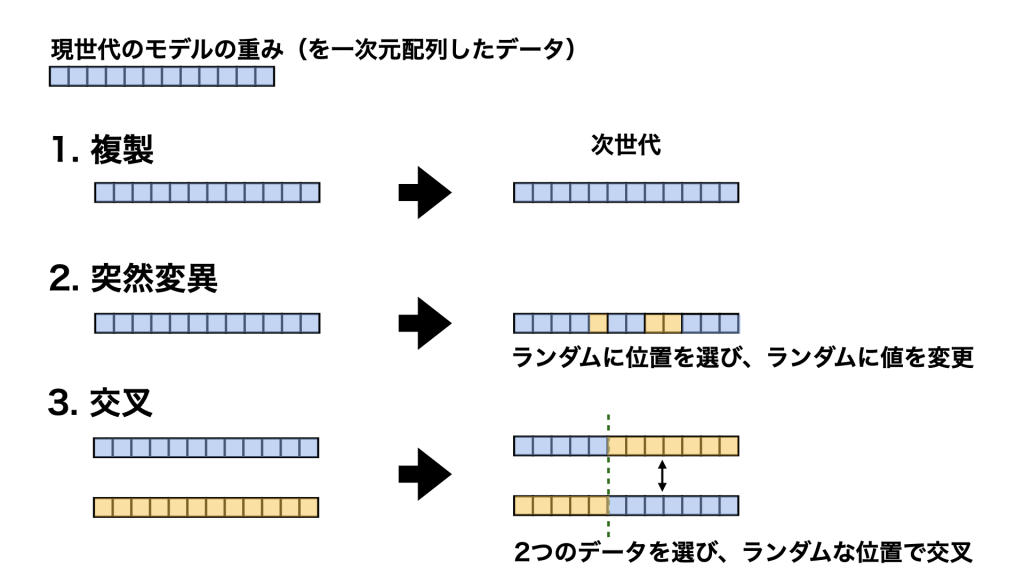
図1. 次世代のエージェントの作り方
3.実験と結果
3-1. 単純な環境での進化
まずは餌場が一つしかない単純な環境でエージェントを進化させます。コードはこちらのものを実験用に少し修正して使いました。ちなみに環境は固定です。エージェントの初期位置をランダムに設定、エージェントは位置情報は持たない(= 周囲の餌の状態だけ検知する)ので、環境を固定してもエージェントはズルして進化することはできません(周囲の餌情報で行動を決めるしかない)。動画2は100世代進化させた後、適応度が最も高いエージェントの動画です。
動画2. 実験3-1の100世代目で最も適応度の高いエージェント
世代毎の適応度を計算したものが図2です。1世代につき51個体おり、その平均、最高値、最低値を書いています。図より集団の平均値は10世代まで上がっていきその後ほぼ平坦になり、進化が完了したようです。一方で最高値は既に3世代ほどで100世代目とほぼ同じ値になっています。環境が単純だったためすぐに最高値を出す進化をしてしまったようです。一方でおもしろいのは、100世代目になっても最低値は小さいままだということです。次世代を作るとき突然変異を行っているため、集団の中に適応度の低い「異端児」たちが常に存在するのです。集団の平均値は上がっているので、集団全体の適応度は上がっている(= おそらくほぼ同一の動きをするように進化した)一方、このような異端児が常にうまれるようなアルゴリズムになっています。
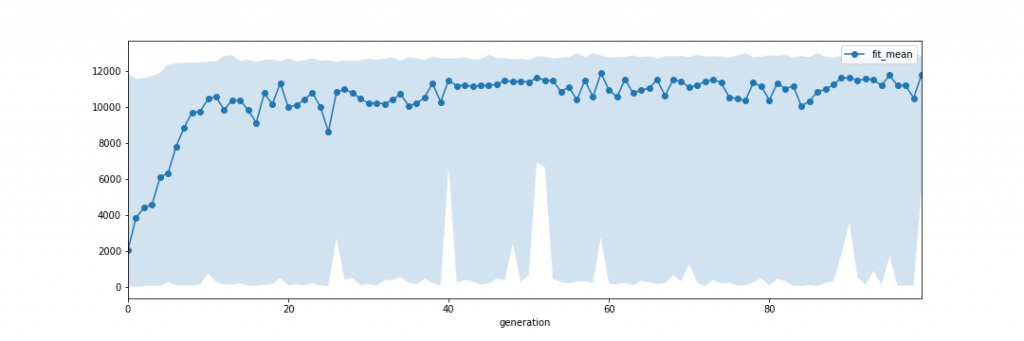
図2. 実験3-1の世代ごとの適応度の変化(x=世代、y=適応度)。実線は世代の平均値。色が塗ってある領域の上端と下端は、世代の適応度の最大値と最小値に対応。
3-2. 交叉は必要か?
ところで次世代をつくるときに「交叉」(図1参照)は必要でしょうか?生物とのアナロジーでいえば交叉は有性生殖にあたると思います(突然変異は無性生殖?)が、今回のような単純なモデルでは不要な気がします。ここではその実験をしてみましょう。実験3-1と設定は同じにして、次世代の集団をつくる際に交叉をなくしました(コピーと突然変異だけ)。100世代目は下図のような動きになります。
動画3. 実験3-2の100世代目で最も適応度の高いエージェント
ほとんど変化ありませんね。実際、世代ごとの適応度を見てもほとんど同じです(図3参照)。適応度が平坦になるまでの世代数が~20と実験3-1より多めにかかっていますが、これは初期値の問題で本質的ではないとお思います(初期データはランダムに設定しているので実験3-1と異なり、実験3-1の方が初期エージェントの適応度は高いように見える)。環境が単純だったためかこの実験では進化に交叉は不要という結論になりました。
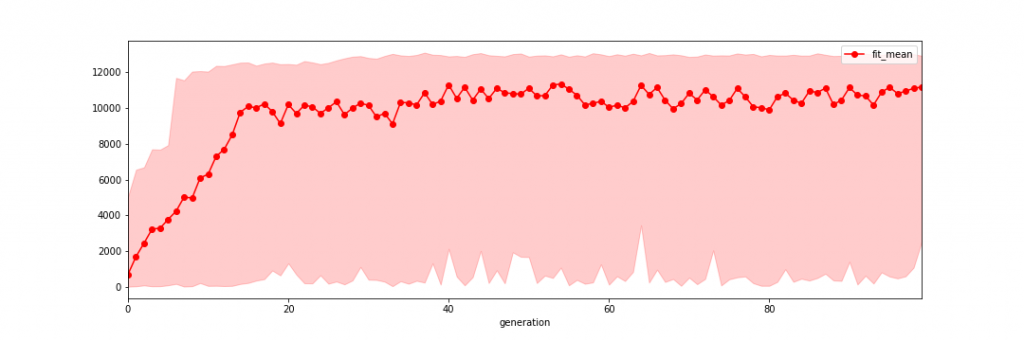
図3. 実験3-2の世代ごとの適応度の変化(x=世代、y=適応度)。実線は世代の平均値。色が塗ってある領域の上端と下端は、世代の適応度の最大値と最小値に対応。
3-3. もう少し複雑な環境では?
上記3-2は環境が単純すぎたのがいけないかもしれません。餌場が複数ある少しだけ複雑なケースで実験してみます。環境を変更した以外は手法は変更せず、交叉あり・なしの場合で100世代進化させました。以下が結果です(動画4, 5)。ほとんど違いはないように見えます。また世代毎の適応度を見ても大きな違いは見られません。まだ環境が単純なのか、それとも今回使ったニューラルネットと相性がよくないのか、いずれにせよ今回の実験では「交叉は不要」とう結論になりました。ちなみに実験3-1, 2と比べると環境が複雑な分だけ適応度が平坦になるまでの時間がかかっているのがわかります。
動画4. 実験3-3の100世代目で最も適応度の高いエージェント(交叉あり)
動画5. 実験3-3の100世代目で最も適応度の高いエージェント(交叉なし)
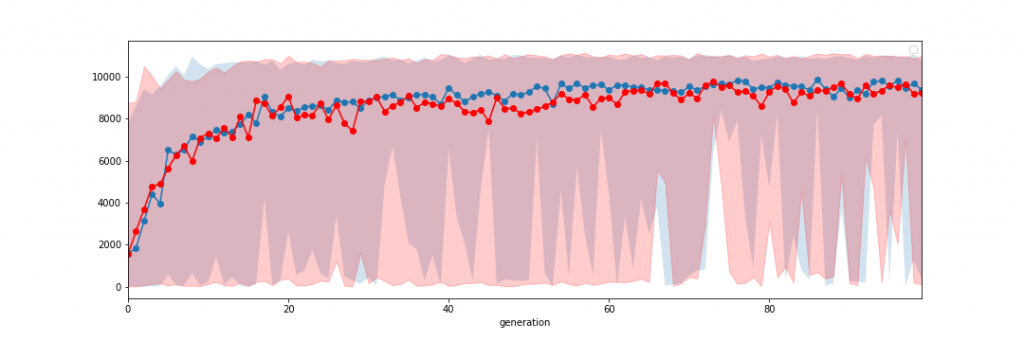
図4. 実験3-3の世代ごとの適応度の変化(x=世代、y=適応度)。実線は世代の平均値。色が塗ってある領域の上端と下端は、世代の適応度の最大値と最小値に対応。青は交叉あり、赤は交叉なし。
まとめ
遺伝的アルゴリズムについて、強化学習的な環境でエージェントの進化の実験をしました。エージェントの行動を決めるアルゴリズムにはニューラルネットを用い、適応度が高くなるようにニューラルネットの重みを進化させました。今回の実験は環境やモデルが単純だったためか、次世代を作成するときに交叉の手法は不要で、突然変異だけあれば十分だとわかりました。遺伝的アルゴリズムの面白いところは、世代が進んでも多様性を失わないところです。アルゴリズムの本質からして、適応度が高いものだけでなく低いものも抱えて進化するようになっています。強化学習の手法などと比べると、最適化を目指すというよりは環境への頑健性を持たせているように思えます。今ある環境に「最適」な種だけでなく多様な種が存在できるため、環境変動への頑健性が持てるのではないかと推測できます。このことはわれわれ生物が環境変動により幾度もの大絶滅を繰り返しながらも、誕生から30億年たった現在も地球上に繁栄していることからも納得ですね。遺伝的アルゴリズムの良さを理解するには、もう少し複雑な環境で実験するのが良いと思うので今後試していきたいと思います。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD