2019.10.09
強化学習(PPO)によるFX取引の実践
こんにちは、次世代システム研究室のK.Nです。今回のテーマは、「強化学習で金融取引」です。これは割と昔からよくあるテーマですが、今回はどちらかというと強化学習の基礎を学ぶというモチベーションで取り組んでいます。結論から簡単に言うと、一通りの数値検証まで行きましたが、実用レベルの性能はまだまだという感じでになっています(もし、そんな簡単に儲けることが可能だったら、みんなやっているわけですし)
本記事では、まず強化学習の概要と今回使用したアルゴリズムPPO2について簡単に紹介します。それから、強化学習をFXに適用した結果について示します。
強化学習について
強化学習について、今回の金融取引を例にして説明します。強化学習では、行動の主体者である「エージェント」, 及び、それと相互作用する「環境」の2つのエンティティが存在します(図1参考)。
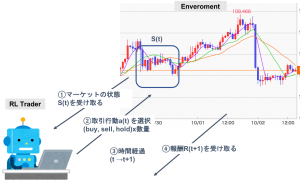
図1:強化学習による金融取引の概要
今回の例では、エージェントが取引を行うトレーダー、環境が対象とする資産の価格に関する情報を提供するマーケットになります。エージェントと環境は以下のようなやり取りしながら、経験を蓄積していきます。
- エージェントは環境から状態を受け取ります。状態はその時点までのマーケットの情報です。
- エージェントは環境から受け取った情報をもとに、ある行動をとります。今回の例だと、対象資産を購入するか、売却するか、保持するか? 注文する場合は、その数量に関して指定します。
- エージェントの行動の結果、環境から報酬を得ます。今回は、エージェントの保有資産価値(NetAssetValue)になります。
- 1-3を終了条件に達するか、時間が上限に達するまで繰り返します。
上のような手順によって、得られた一連の結果をτ=(s1, a1, r2, s2, a2, r2, ..)をMDP(Markov Decision Process)と呼びます。ただし、強化学習の目的は、与えられた状態を元に「最適な」行動を取るエージェントを作ることです。平凡な行動しか取れないエージェントに用はありあません。ここで、最適な行動を定義するベースとなるのが、累積報酬の割引現在価値です。常にこの値を最大とするような行動を取るようにエージェントを学習させるのが強化学習の目的となります(強化学習と呼ぶのも、報酬によってエージェントの行動を強制(reinforce)させるているからですね)
そして、強化学習の学習アルゴリズムは現時点においても様々な手法が提案されています。これは、次節以降で簡単に紹介します。ただ一方で、見落としがれがちですが、強化学習の性能を決める重要なファクターは他にもあるということです。
まず、環境の状態をどう定めるかという問題があります。例えば、ゲームだと画面の映像、囲碁や将棋だと盤面の情報などが環境の状態としてほぼ必要十分に成り立ちますが、金融の場合、資産のプライスデータだけではなく、関連する資産の価格データ、マクロ情報、市場センチメント、アナリストレポート等簡単に思いつくだけでもかなりの候補がでてきます。このように、含めるべき情報を取捨選択していかなければいけません。また、状態を生データのままで与えず、加工(特徴量エンジニアリング)することも必要になってきます。
強化学習アルゴリズム(PPO)
強化学習は現状、さまざまな手法が提案されています(図2参照、引用元)。ここでは、個々モデルについての詳細は割愛し、今回採用したPPOに関連する所のみ説明します。
図2:最近の強化学習アルゴリズム
まず、Model-Free, Model-Basedの違いです。これは環境の状態遷移過程について(何かしら近似的に)モデルを導入したかということです。Model-Freeの場合、実際に施行を重ね取得したモンテカルロパスを利用し、学習を行います。この方法は、ロボットのような実際に動作させて結果のサンプルを取ることが高コストとなるような領域の場合、学習効率がたいへん悪いので、Model-Basedの方法による解決が提案されています。ですが、今回の対象はModel-Freeになります。
そして、Model-FreeにはQ-LearningとPolicy-Optimizationがあります。
まずQ-Learningについてです。、これは最適行動価値関数(Q関数)を推定するというアプローチを取っています。この最適Q関数自体は最適ベルマン方程式を解くことで求めることができます。このQ関数にDNNを用いた手法がDQNと呼ばれる代表的な手法です。この手法はAtariのゲームで高性能を出したことで話題になりました。
一方、Policy-Optimizationは、方針(Policy)を直接パラメトリックな関数で表し、割引報酬の累積価値の期待値を最大にするようなパラメータを決定します。ポリシーの勾配の期待値は、モンテカルロ平均で求めることができ、不偏推定量ですのでサンプル数が多いと理論値に収束します。しかし、実用可能な試行回数程度では期待値の分散が大きく、収束しないという問題があります(下の疑似コード参照)。

この勾配計算の安定性を高めるための方法が幾つか提案されています。
Actor-Critic
割引報酬の累積価値に価値関数を引くことで、勾配のサンプル平均の分散が減らすことができます。パラメータに関係のない任意の関数を引いても、期待値に影響を与えません(つまり、不偏推定を維持)。かつ、平均値の分散が減り、期待値計算の安定性が高まります。このようなテクニックをベースライン除去と呼びます。Actor-Criticでは、Policy(Actor)と価値関数V(s)(Critic)を共にNN関数で表現し、学習対象とします。こうすることにより、PolicyGradientの精度が向上します。
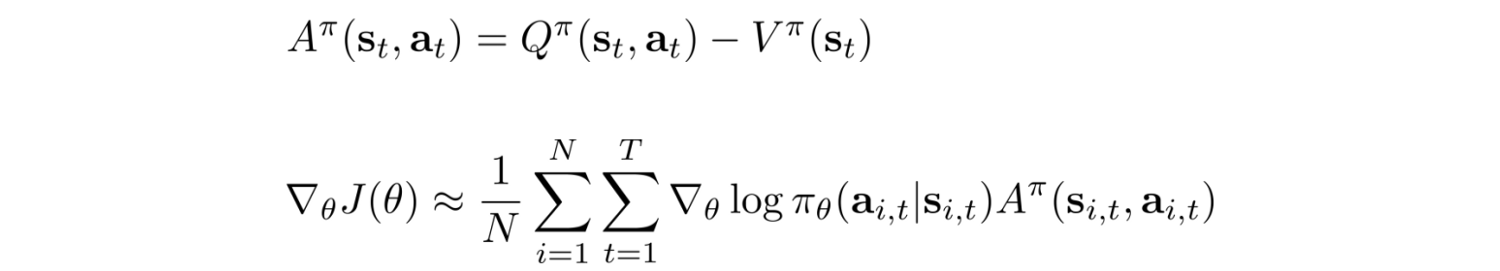
Off-Policy
勾配のパラメータ更新の度に、モンテカルロパスを計算するは非効率です。これをOn-Policyと呼びます。それに対し、Off-Policyでは、古いパスを再利用しながら、パラメータ更新します。パラメータ更新を複数回繰り返したら、パスを発生させた古い方針を新しい方針に置き換えます。パラメータを更新する度に、多くのモンテカルロパスを発生させる必要がなくなるので、効率的です。
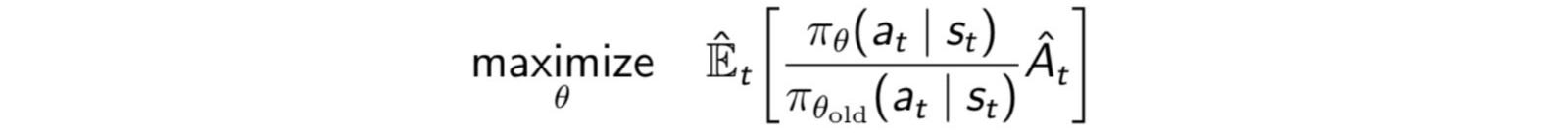
PPO
ただし、もしパラメータ一更新の際、方針が大きく変わると、パスを計算している古い方針からのずれが大きくなり、勾配の計算が収束せず、効率が著しく悪くなるという問題が生じます。そのため、方針を改善しつつも、パラメータの一回の更新で方針を大きく変更しすぎないことが必要になります。そこで、提案されたのがPPO(Proximal Policy Optimization)という手法です。これは、新旧のポリシーの確率の比率rを計算して、その値がしきい値以上超えると、打ち切るという方法をとっています。
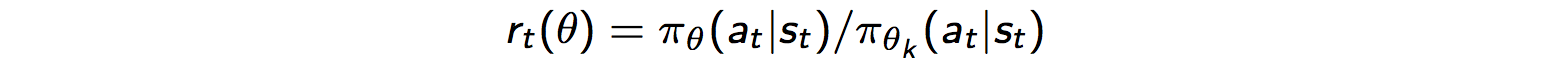
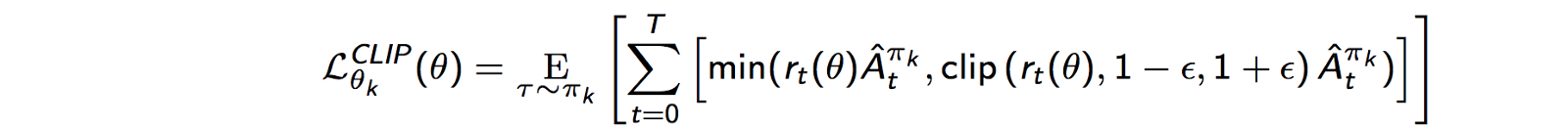
図3はAdvantageの正負ごとにrに対するLのグラフです。Lが増大する方向へrが一定以上変化すると、打ち切られる事が分かります。これにより、その方向へ過度にPolicyが変化するのを防ぐことができます。
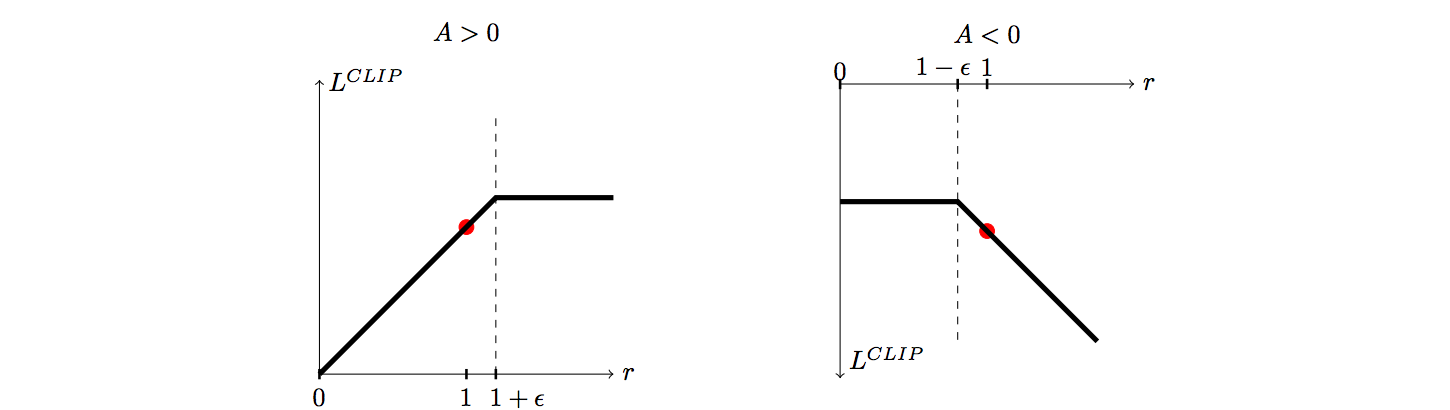
図3:PPOの目的関数Lのrに対するプロット
PPOのアルゴリズムは次のとおりです。
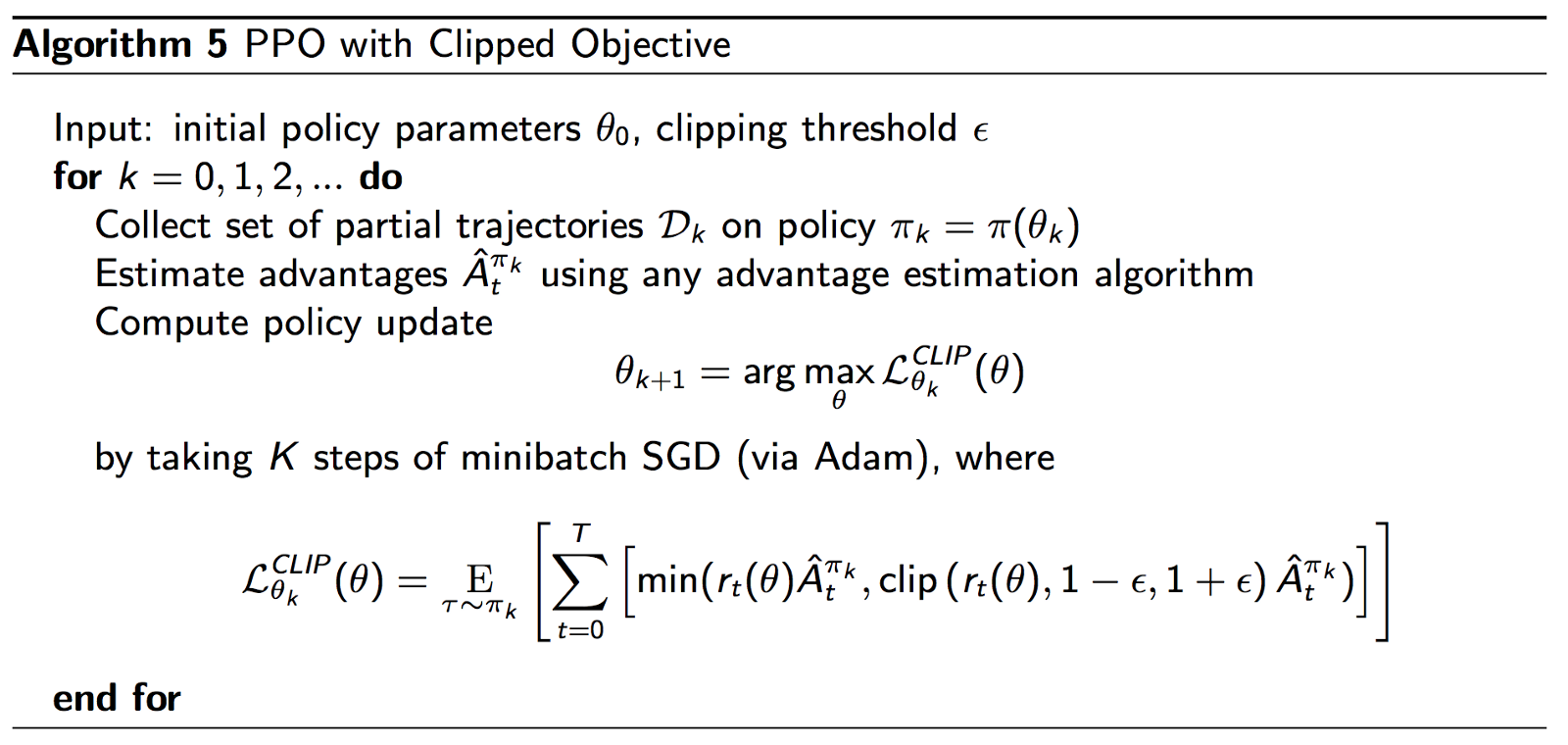
金融取引への適用
それでは、今紹介したPPOを使って、実際の為替データを使って、機械学習によるFX取引を行っていみたいと思います。
準備
設定
•データ: Forex(USD/JPY)の1分足データ(OHLC)を使用
•強化学習の環境
以下の実装をベースに適宜修正.
https://github.com/pipatth/PPO2-currency-trader
•強化学習フレームワーク:Stable Baselines
https://github.com/hill-a/stable-baselines
取引条件
- 初期費用:10万円
- レバレッジ:25倍
- ロスカット:証拠金維持率が50%以下
- スプレッド: 0.003円
注文価格について
1分足のOHLCのプライスデータからどうやってbid, askを作るかという疑問があります。シンプルな方法として以下の方法があります。
- closeをそのままbidとして採用. askはスプレッド分上乗せ.
- (Low, High)の間を一様乱数で生成し, bidとする. askは1と同様.
今回は2を採用しました。
Environmentの設定
- Observation: 過去30分までのOHLCデータ. つまり、(31×4)次元の実数
- Return: NAV(Net Asset Value) = 現金+含み損益
- Action: 取引タイプx数量. 取引タイプはBuy, Sell, Hold.数量は現時点最大ポジションを10として、1から10まで選択.
学習条件
- Train期間: 2019/1 – 2019/7
- Test期間: 2019/8
- モデル:PPO2(パラメータの条件は初期設定を使用)
学習の様子
強化学習に限らず、機械学習ではTrainingの過程を監視しておく必要があります。例えば、学習過程の可視化にTensorBoardを使うと大変便利です。今回の例では、割と初期の段階でRewardsの改善が止まっている様子がわかります。
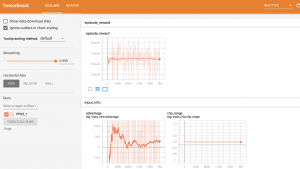
図4:TensorBoardによる学習過程の可視化
結果
まずは、8/5から8/9までの一週間、初期費用10万円から取引を始めた場合を見てみましょう。図5はその結果です。図6はその一部の期間を切り抜いたものです。図4の1段目に注目すると、全体的に「売り」のほうが「買い」より多くなっている様子がわかります。2段目のポジション保有量と3段目の売買注文量を見ると、より状況はわかりやすくなります。細かく売りポジションを増やしながら、一気に大きい単位で買い注文を出し、ポジションを解消している様子が分かります。ある程度ポジションが積み上がると、基本的にそれを解消しようとする圧力がかかるので、この現象は自然です。しかし、基本的に売り注文優勢である理由は、今回のTrain期間のドル円の値動きにおいては、そのような振る舞いが有利だったからという可能性は考えられますが、実際のところ根本的な理由はわかっていません。結果のより詳細な解釈については、今後の宿題とさせてください。また、4段目はReturnであるNetAssetValueの値です。大きなドローダウンを経て、最終的な資産は11.5万円になっています。
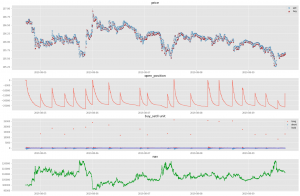
図5:RLの結果, 期間は8/5-8/9。1段目はプライス、Buyが赤、Sellが青で表示。2段目は保有ポジション。3段目はBuy, Sellした量の表示。4段目はReturnであるNAV.
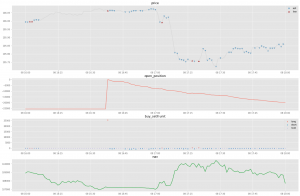
図6:図5の一部切り取り(8/8 16:00-18:00)
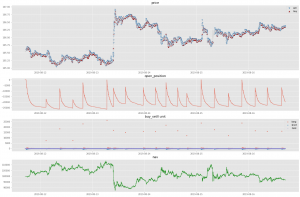
図7:RLの結果, 期間は8/12-8/16。
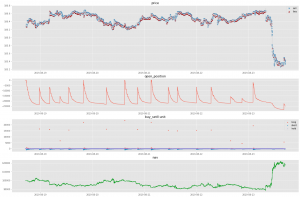
図8:RLの結果, 期間は8/19-8/23。
図7, 8は8月のさらに2週分(8/12-, 8/19-)の結果です。最終的なNAVはそれぞれ9.6万円、11.8万円です。今回のような単純な検証では、まずまずな結果なようにも思えます。
今後の課題
今回は複雑なことはせず、なるべくシンプルな設定で強化学習をFX取引にただ単に適用したにすぎません。今後は、以下の観点で修正を行い、改善を目指していく必要があると考えられます。
- Environmentの最適化。例えば、Stateとして、対象資産と相関の高い変数や高次情報(テクニカル指標)を含める。また、Returnも本当にNAVでよいか?
- Modelの設定。例えば、PPO2のNN関数にLSTMを用いることで、Modelが過去の情報を保持し続けることが可能→精度UP?
- Robustな性能評価。Test時期によって結果が変わる、安定しないという問題。
最後に
次世システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。
一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD