node2vecの論文紹介
こんにちは次世代システム研究室のJK（男）です。最近グラフデータに興味を持ちつつあるので、今回は気になった論文の簡単な紹介をします。紹介する論文はnode2vecです。
グラフデータとは、ノード（頂点）とノード間の連結関係を表すエッジ（枝）で構成されるデータ構造のことです。エッジに重み（どのくらい強く結びついているか）の情報が付加される場合もあります。たとえば、Facebookのユーザー（ノード）とユーザー間の友達関係（エッジ）をつなげていくと、巨大なグラフができますね。あとよく言われるのは、空港（ノード）とその間をつなぐ航路（エッジ）とか。ハブ空港という単語を聞くこともあると思いますが、たくさんのエッジを持っている空港と解釈できます（＝多くの空港からの発着便がある）。グローバル化・IT化による物理空間・デジタル空間でのつながりが広がるなか、グラフデータの理解はこれからますます重要になってくると思います。
グラフ構造は非線形的で数値計算による扱いが少し面倒です。昨今のデータ解析ブームにのっかり、グラフデータもうまく数値計算できるように加工しようという流れがあり、この論文はその手法を提案するものです。簡単にいえば、ノードやエッジ情報をベクトル化するってことですね。上記の課題として、グラフ構造を情報損失なしで（or 少なく）ベクトルに射影する方法が確立されてないことです。もう一つの課題は、グラフ構造はノード数が増えると取り得る経路が増えてしまい、大きなノード数では計算コストが爆発的に増えてしまうことです。
今回紹介する論文は上記課題を克服するために、グラフ構造のベクトル化の新しい方法を提案しています。またこの方法を使えば、計算コストも抑えられるらしいです。以下では、この論文について解説していきます。ちなみに既に別の日本語記事（これとか）がありますので、そちらも参考にしてください。この記事では、厳密さよりも直感的に理解できるように説明していきます。
以下、図3以外の画像は論文からの引用です。
node2vecの原理（論文の解説）
1.概要の説明
ここではnode2vec全体の流れを理解してもらうために、提案手法の概略を説明します。詳説は後の章で行います。グラフ構造をベクトル化する方法は色々あると思うのですが、論文の手法では
- グラフ構造からサンプリングして、シークエンスデータを作る。
- 上記データをトレーニングデータとして用いて、教師なし学習でノードとエッジの情報をベクトル化する。
プロセス1は面白いですね。理学では現実のデータを抽象化して”真の分布・式”を導く方向なのですが、ここでは逆です。すなわち”真の構造”が与えられているが、そのままでは扱いづらいので”現実データ”に書き下しています。より具体的には、グラフの情報を複数のシークエンスデータに変換します。書き出したデータをマシンパワーでガリガリ解いてやろうという考えですね。マシンパワーありきの現代っぽい考えと言えます。
プロセス1で大事になるのは、グラフ構造という”真の分布”からデータ量をできるだけ損失せずにサンプリングする事です。この論文の最もオリジナルな部分は、このサンプリング方法を新しく提案したことにあります（具体的な方法は次章）。プロセス2では、トレーニングデータの情報を説明するベクトルを作成するアルゴリズムが必要です。ここでは自然言語処理で使われるskip-gramという手法を採用しています。この部分は論文独自のものではありませんが、面白い考えなので次の章で説明します。
2.個々のプロセスの説明
2-1. プロセス1: サンプリング → シークエンスデータ
基本的な考えは単純です。あるグラフ構造（ノード、エッジ、エッジの重み）を考えます。ノードAを起点に考えたとき、エッジ重みを考慮してステップ数kでランダムウォークさせます（=重いほどつながりが強い→よく通るように確率を設定）。これを試行数r回繰り返します。すると、シーエンス数kのデータがr個入手できます。ランダムにサンプルしているのでデータはそれぞれ異なりますが、”ノードAの近傍のノードが含まれる”, “ノードAとつながりが強いノードほど出現頻度が高くなる”という共通点を持つことがわかると思います。つまり、ノードA近傍のグラフの特徴（＝情報）をシークエンスデータに書き下せたと言えます。このサンプリング手法には2種類の極端なケースが考えられ、BFS(breadth first search)とDFS(depth first search)と呼ばれています。図１の通り、BFSは幅優先探索で、ノードAと接続しているノードを優先的に探索（サンプリング）します。DFSは深さ優先探索で、ノードAからできるだけ離れたノードに到達するように探索します。
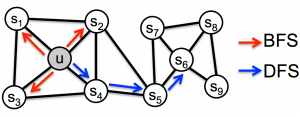
図１．BFSとDFSの概念図
上記２種のサンプリングの違いは、取り出すグラフの情報に対応しています。グラフ情報には大きく分けると2種類あります（と論文には書いています）。一つはmophily、もう一つはstructual equivalenceです。前者は、端的にいえば同じグループに属しているか（ノードAと密接な関係があるか）、後者は似たような構造を持っているか（たとえばノードAがハブ構造を持つとしたら、ノードAから離れたノードXもハブ構造だった場合、両者の構造は似ているといえる）。そしてmophilyの情報はDFSによって引き出しやすい一方、structual equivalenceの情報はBFSで引き出しやすいです。これはDFSがAの近傍を探索するためA近傍のつながりの情報が引き出せるのに対して、BFSはAにフォーカスして情報を引き出すからです。このようにサンプリング方法によってグラフ構造から抽出できる情報は変わるのでサンプリング手法は重要です。
この論文では、新しいサンプリング手法として以下を提案しています。
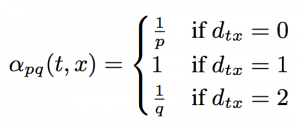
式1. 提案手法の遷移確率の（重み補正）式
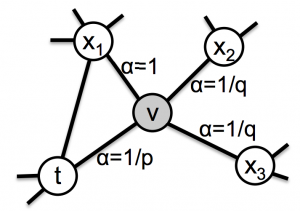
図2. 提案手法の遷移確率（重み補正）の概念図
なんのこっちゃですが図２を見るとわかりやすいです。ノードtからノードvに移動したケースを考えます。式1は、vから次のノードへの探索するときの、各ノードへの確率（を計算するための補正値；実際の確率は、エッジの重みwをかけたαwに比例）を計算します。面白いのは、遷移を考えるとき、遷移元ノードvでなく、さらに1step手前のtを起点にしている点です。式のdは、ノードtとノードx（vの遷移先）の距離です。
- d=0は、ノードtのことなので、t -> v -> tと戻ってくるパス
- d=1は、tとつながっているノードのことです（図2のx1）
- d=2は、xとはつながっているが、tとはつながっていないノード（図2のx2, x3）
大事な点はp, qというパラメータを導入している点です。従来の手法では、サンプリング方針は固定化されており（抽出情報の偏りが固定化されるので）課題によって得手不得手がありました。しかしパラメータを導入することで、課題ごとにp, qを適切に設定して、課題に適切な情報抽出が可能になります。パラメータは課題ごとに半教師あり学習で決めていくのですが、ここでは説明は割愛します。興味のある人は元論文を読んでみてください。
2-2. プロセス2: サンプルデータ → ベクトル
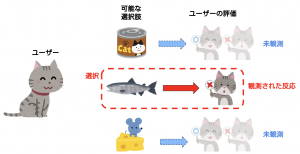
2-1の手法で、ノードA近傍の情報をノードAの情報として取得できます。ここからどうやってノードAの情報を抽出するか？ここが個人的には最も面白い点でしたが、自然言語処理のskip-gramという手法でベクトル化します。なぜそれが可能なのか？Skip-gramはword2vecの実装手法の一つで、自然言語処理において「単語をベクトル化」するための手法です。詳細な説明はここなどにゆずりますが、簡単にいえば、”単語A”（たとえば”猫”）をベクトル化するため、単語Aが出現する文章をたくさんサンプルしてきて、その近傍にある単語群の情報を元にベクトル情報にするということです。たとえば図3では、”猫”という単語は「ペット」や「飼う」といった単語の近傍にあることがわかり、「これらの単語と関係性の強い単語である」という情報をベクトルとして”猫”を表現します。想像できると思いますが、”犬”も似たような文章があるはずなので、”犬”と”猫”のベクトルは類似することが期待できます。
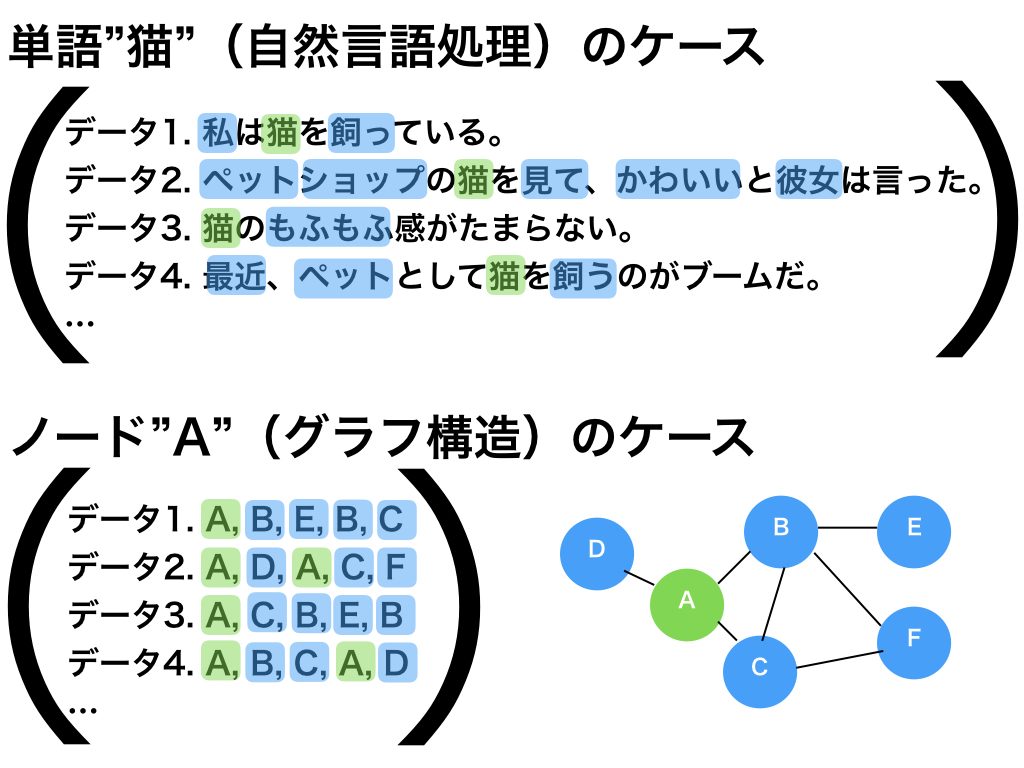
図3. 文章（自然言語処理）とノード近傍のサンプルデータの類似性
上記の説明でピンときた人もいると思いますが、実は単語A, 単語B…をノードA, ノードB…に変換すれば、2-1でサンプルしたデータを単語のケースと同様の手法でベクトル化できます(図3参照)。ノードAのベクトル化とは、周囲のノードとの関係性の情報化といえるので、上記の自然言語処理のケースと全く同じですね。node2vecという提案手法の名前もword2vecをもじったものですが、これだけ似ていれば納得です。学習結果は2-1でサンプリングしたデータの質に依存するので、サンプリング手法がいかに大事かもよくわかると思います。
3.実験
3-1. 教師あり学習を用いた評価
ここではnode2veでベクトル化を行い、そのデータをfeatureとして教師あり学習を行います。目的はnode2vecのベクトル化の精度を（間接的に）評価することです。ベクトル化が精緻に行われれば、より良い情報がfeatureとしてinputされるので、教師あり学習の精度も向上するだろうという考えです。
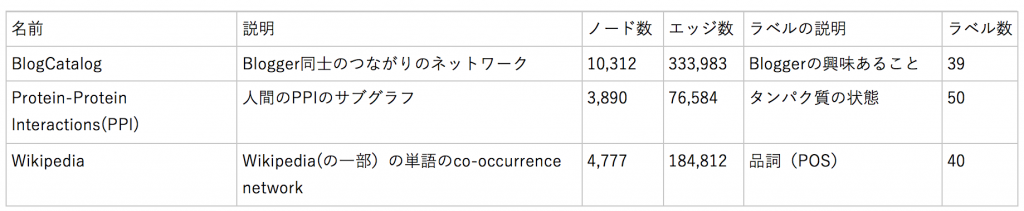
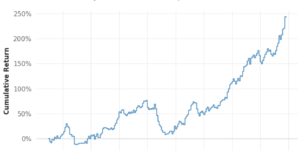
評価に用いたデータは上記の３種類です。一応、PPIとco-occurrenceの説明リンクです。グラフ構造のデータが色々な分野に存在することがわかりますね。どのデータのノードにもラベル付けされており、教師あり学習ではそのラベルを予測します(Multi-label分類のロジスティック回帰)。パラメータ値などの詳細は論文を見てもらうとして、結果は図4のようになります。評価値には（多クラスなので）Micro-F1スコアとMacro-F1が使われています。横軸は全データのうちトレーニングに使う比率です。当然、多い方が評価値はよくなりますね。図中のSpectral Clustering, DeepWalk, LINEとはベクトル化の別手法です。node2vecは既存の手法より精度良いですよーと言いたい図なのですが、ここではその話はスルーします。
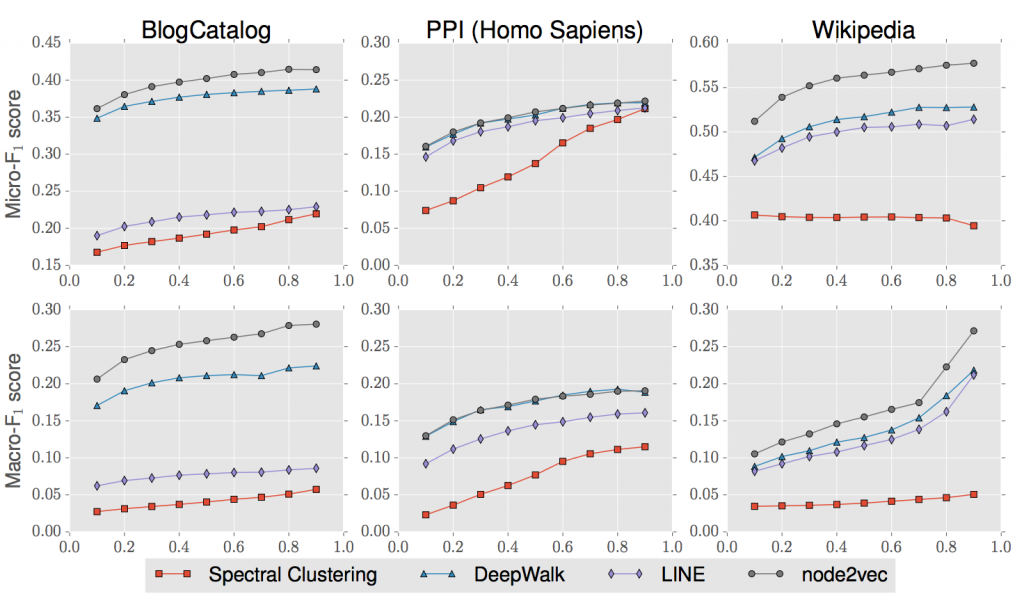
図4. 3つのタスクの評価値
ここで図4を紹介した理由は、上記テーブルのように全く性格が異なる情報でもp, qをうまく調整することで、node2vecは良いパフォーマンスが出せるということです; (p, q)の値は、BlogCatlogで(0.25, 0.25), PPIで(4, 1), Wikipediaで(4, 0.5)。たとえばDeepWalkも良い手法に見えますが、Wikipediaタスクはあまり得意でないように見えます。ノード数に対してエッジ数が多いグラフ構造なので、この辺りが原因なのかもしれません。一方、node2vecではp, qを調整することで、高いパフォーマンスが出せているように見えます。
3-2. パラメータとモデル精度の関係
ここではnode2vecのハイパーパラメータを変化させたときのモデル精度の変化を測定して、ハイパーパラメータとnode2vecの精度を間接的に推定しています。教師ありデータには3-1でも使ったBlogCatalogデータを使います。測定したパラメータは、遷移確率パラメータpとq, ベクトルサイズd, サンプリング試行回数r, サンプリング毎のstep数l, コンテキストサイズ（= skip-gramを計算するときのwindow size）k, の6種類です。結果は図5です。p, qは下げた方がよくなるようです（特にq）。ただしこれは課題に強く依存します。BlogCatalogはグループのクラス分け問題でDFSよりのサンプリングが精度が良くなるはずで、このような結果になったようです。ベクトルサイズは表現できる情報量を反映するので影響大きいですが、ある一定以上の大きさになれば十分な表現能力を持つので精度改善はサチります。rとlはサンプリングの精度に直接関係して、rが多ければ多いほど、lが長ければ長いほど、サンプリング精度は上がるのでモデル精度も上がります。ただしその分だけ計算コストが増えるので、計算コストと精度改善のトレードオフを考える必要があります。kは10以上ならあまり影響がないですね。これは自然言語処理のときも似たような傾向にある気がします。
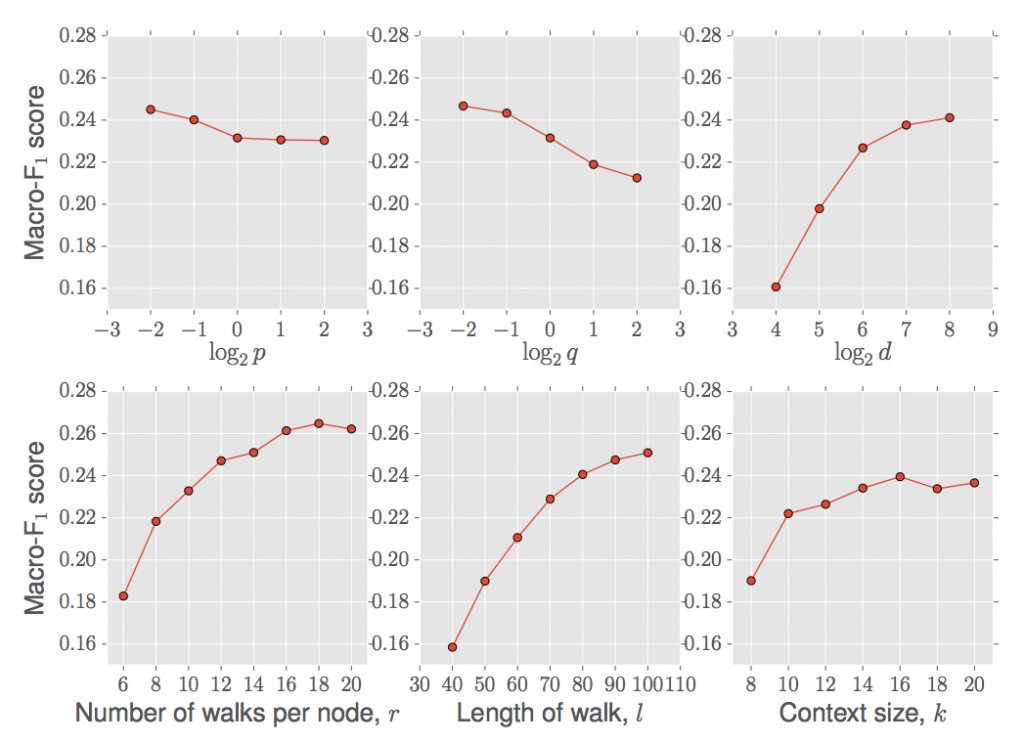
図5. パラメータとモデル精度の関係
3-3. 計算コスト削減の工夫と結果
これまでは、「グラフ構造の情報量保存」の手法部分にフォーカスしていましたが、もう一つ課題：「計算コストの爆発的な増加」がありましたね。今回の手法ではサンプリングする際に、サンプリングしたデータを再利用することで計算コストの削減しています。たとえば、ノードuから出発したサンプリングデータ: {u, s4, s5, s6, s8, s9}を取得したとします。k=3だったとき、uから出発した{s4, s5, s6}, s4から出発した{s5, s6, s8}、s5から出発した{s6, s8, s9}を取り出します。もちろん、個別ノード毎にサンプリングした場合に比べてバイアスはかかりますが、計算コストは下げられます。またベクトル化の学習でも、negative sampling（skip-gramではデフォルトの採用手法）やasynchronous SGD（分散マシンでのトレーニングで、待ち時間を減らすSGDの手法）を採用して、学習コストを下げる工夫をしているようです。実験として、Erdos-Renyiグラフという構造のグラフデータについて、node数を増やしたときの計算コストを測定しています（図6）。100万個のノードの計算が数時間で終わっているので良さげに見えますが、（私が見逃したのか）マシンスペックがわからないので、この計算時間がどの程度すごいのかわかりません。。少なくともノード数nに対してべき乗の計算時間なので、実用レベルでも十分に使えそうです。
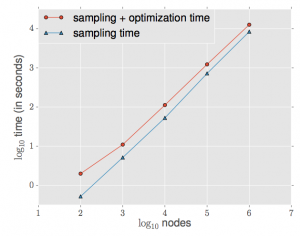
図6. node数と計算時間の関係
まとめ
node2vecの論文について紹介しました。まだ荒削りな印象はあるので、より洗練された手法が出てくるのかなという印象もあります。画像や自然言語処理のお化けみたいなネットワーク構造と比べると、まだまだ発展途上で、アイデア次第で全く異なる面白い手法などが提案されるかもしれませんね。これからもこの界隈を気にかけていきたいと思います。次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
