ビジネスで利用する因果推論実践 ~アンチパターンを添えて~

こんにちは。次世代システム研究室のY. O.です。

前回の記事では、筆者が共に働いている、スマホアプリを運営するグループ会社のチームで取り入れている因果推論手法について紹介しました。
今回は、ABテストのようなコントロールされた環境下で施策を実施することができないケースにおいて利用される種々の因果推論手法について、実際にデータを用いながら結果を考察していきたいと思います。また、それぞれの手法で陥ってはいけないアンチパターンの再現も行ってみました。

データサイエンティストとして「アプリユーザー体験改善 を定量評価し、ビジネスの成功 につなげる因果推論」について、早速手を動かしていきましょう！

1. 本記事で行うデータ解析の概要

ビジネスケース

• 本施策の目的
  • ユーザーの愛着度を上げるキャンペーン施策を行い、アプリを開く日数を多くする
• 本施策の実施方法
  • 愛着度が低いユーザーほどキャンペーンが適用される確率が高くなるように、全ユーザーの20%にキャンペーンを適用する
• 本施策の測定指標
  • ユーザーあたりのアプリを開く日数

データ解析のオーバービュー

1. データ生成
   • 今回のケースに合致するデータをkaggleで数時間探したが、見つからなかった（マーケティング系のデータって全然ない…）
   • ユーザーがアプリを開くかどうかを定式化し、その式をもとにデータを生成した
2. 複数手法による施策評価
   • 差の差分法・IPW推定・傾向スコアマッチングを用いて、生成データ内の真のキャンペーン効果を正しく測定できるかを評価
   • それぞれの評価において、各種手法の弱点をつくような考察を実施

2. 実験データ作成

より実際に近いシチュエーションを作り出すにはどうすれば良いか、本記事で最も苦戦した部分になります。
結論、次のデータ生成過程でデータを生成することにしました。

pはある日にアプリを開くかどうかの確率値であり、愛着度（= engagement）の作用と、季節要因の作用により決まるとしました。季節要因の部分について、Lは周期であり、aはengagementを(1 – a) ~ 1倍にする拡大作用を持っています。
engagementはアプリへの愛着度を定式化したものであり、x1 ~ x4の説明変数で構成されるとしています。（この説明変数は、後の傾向スコアを用いた解析において、介入に含まれるバイアスを取り除く共変量として利用します）

まず初めに、ユーザーごとの説明変数とengagementを生成してみます。
以下がサンプルコードです。イメージとしては、各特徴量x1 ~ x4が0 ~ 1の確率値となるように、x1 ~ x4に任意の相関を持たせつつ、その共役事前分布であるベータ分布からデータを生成する感じです。

import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler

import matplotlib.pyplot as plt
import seaborn as sns

def generate_engagement_dataset(n_users=10000):
    '''
    ユーザーの特徴量とengagementを生成する
    '''
    # データ生成時に利用する、特徴量間の相関係数を設定する
    cor_12 = 0.4
    cor_13 = -0.5
    cor_14 = 0.3

    # engagementを定義する真の回帰係数を設定する
    b_0 = 0
    b_1 = -2
    b_2 = -1.7
    b_3 = 1.4
    b_4 = 1

    # engagementにおける変動係数の定義
    # （重畳させるガウシアンノイズの標準偏差が、engagementの平均値の何倍になるかを定義する）
    eps = 0.3


    user_feat = pd.DataFrame()
    user_id = [("0"*len(str(n_users))+str(i+1))[-len(str(n_users)):] for i in range(n_users)]
    user_feat["user_id"] = user_id

    seed_1 = np.random.beta(2, 2, n_users)
    seed_2 = np.random.beta(1, 5, n_users)
    seed_3 = np.random.beta(3, 2, n_users)
    seed_4 = np.random.beta(5, 3, n_users)
    x_1 = seed_1
    x_2 = seed_2 + np.sqrt(1 - cor_12**2) * x_1
    x_3 = seed_3 + np.sqrt(1 - cor_13**2) * x_1
    x_4 = seed_4 + np.sqrt(1 - cor_14**2) * x_1

    scaler = MinMaxScaler()
    user_feat["x1"] = scaler.fit_transform(x_1.reshape(-1, 1))
    user_feat["x2"] = scaler.fit_transform(x_2.reshape(-1, 1))
    user_feat["x3"] = scaler.fit_transform(x_3.reshape(-1, 1))
    user_feat["x4"] = scaler.fit_transform(x_4.reshape(-1, 1))

    user_feat["eng_baseline"] = b_0 + b_1 * user_feat["x1"] + b_2 * user_feat["x2"] + b_3 * user_feat["x3"] + b_4 * user_feat["x4"]

    eng_mean = user_feat["eng_baseline"].mean()
    user_feat["eng_baseline"] += np.random.randn(n_users) * eps*eng_mean
    user_feat["eng_baseline"] = 1/(1+np.exp(-1 * user_feat["eng_baseline"]))

    return user_feat

user_feat = generate_engagement_dataset(n_users=10000)

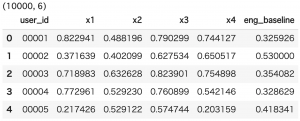
print(user_feat.shape)
display(user_feat.head())

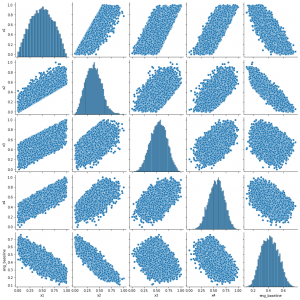
sns.pairplot(user_feat[["x1","x2","x3","x4","eng_baseline"]])
plt.show();

結果は以下のようになり、各特徴量が一定の相関を持ちつつ、0~1に収まる自然な特徴量を作成することができました。（筆者はjupyter notebook環境でコードを実行しています）

続いて、ユーザーごとにキャンペーンが適用されるかどうかを、本施策の実施方法「愛着度が低いユーザーほどキャンペーンが適用される確率が高くなるように、全ユーザーの20%にキャンペーンを適用する」に倣って再現してみます。

def apply_treatment(e, mean_engagement):
    apply_ratio = 0.2
    assert mean_engagement>=apply_ratio, "error"

    apply_prob = (1-e) * apply_ratio / (1 - mean_engagement)
    apply_flg = np.random.binomial(1, apply_prob)

    return apply_flg

effect = 0.05
mean_engagement = user_feat["eng_baseline"].mean()
user_feat["treated"] = user_feat["eng_baseline"].apply(lambda x : apply_treatment(x, mean_engagement))
user_feat["eng_treatment"] = np.clip(user_feat["eng_baseline"] + effect * user_feat["treated"], 0, 1)

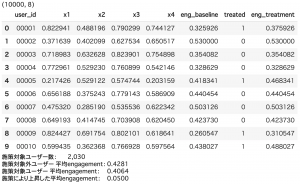
print(user_feat.shape)
display(user_feat.head(10))
print("施策対象ユーザー数：\t{:,}".format((user_feat["eng_baseline"] != user_feat["eng_treatment"]).sum()))
print("施策対象外ユーザー 平均engagement：\t{:.4f}".format((user_feat.loc[user_feat["eng_baseline"] == user_feat["eng_treatment"], "eng_baseline"]).mean()))
print("施策対象ユーザー 平均engagement：\t{:.4f}".format((user_feat.loc[user_feat["eng_baseline"] != user_feat["eng_treatment"], "eng_baseline"]).mean()))
print("施策により上昇した平均engagement：\t{:.4f}".format((user_feat.loc[user_feat["treated"] == 1, "eng_treatment"] - user_feat.loc[user_feat["treated"] == 1, "eng_baseline"]).mean()))ね

狙い通り全ユーザーの20%にキャンペーンが適用され、かつ、engagementが低いユーザーの方がキャンペーン対象となりやすくなっている結果が確認できました。
また、キャンペーン対象となったユーザーは、キャンペーン後にengagementが+0.05されるという状況を作り出しています。

最後にもう一息です。ここまでで生成したユーザーごとのengagementと、ユーザーごとにキャンペーン対象となるかどうかをもとに、ある日にそれぞれのユーザーがアプリを開くかどうかのデータを生成していきます。
冒頭で、アプリを開くかどうかをengagementと季節要因の作用によって定式化しました。今回は、季節要因の周期Lは60日、aを0.2とすることで、60日間かけて、engagementが0.8 ~ 1倍の振動をするような状況を表現することにしました。この振動により、真のキャンペーン効果は、+0.05 × 0.9(振動平均) = 0.045となります。

L = 60
a = 0.2
e_1 = 0.0

df_days = pd.DataFrame(np.arange(L), columns=["date"])
df_days["join_key"] = 1
df_days["seasonal"] = ((np.cos(2 * np.pi / L * df_days["date"]) - 1) / 2 + np.random.randn(len(df_days)) * e_1) * a + 1

user_history = user_feat[["user_id", "eng_baseline", "eng_treatment"]].copy()
user_history["join_key"] = 1

user_history = pd.merge(df_days, user_history, on='join_key', how='outer')
user_history.drop(columns=["join_key"], inplace=True)

user_history["before_after"] = 0
user_history.loc[user_history["date"]>=L/2, "before_after"] = 1

user_history["eng"] = user_history["eng_baseline"]
user_history.loc[user_history["before_after"]>=1, "eng"] = user_history.loc[user_history["before_after"]>=1, "eng_treatment"]

user_history["prob"] = np.clip(user_history["eng"] * user_history["seasonal"], 0, 1)
user_history["observe"] = np.random.binomial(1, user_history["prob"])

user_history = pd.merge(user_history, user_feat[["user_id", "treated"]], on="user_id", how="left")

ここで生成されたuser_historyテーブルは、ユーザーごとに60日分の結果を再現しているので10,000 × 60行のテーブルになっています。また、その日にアプリを開いたかどうかはuser_history["observe"]に格納されていて、engagementと季節要因で作成された確率pのベルヌーイ試行と考え生成されたものになります。
e_1は後の実験で季節要因に摂動を加えたくなったとき用に組み込んでおきます。

生成されたデータを見てみましょう。

x = user_history.groupby("date")[["observe"]].mean()
x.plot()
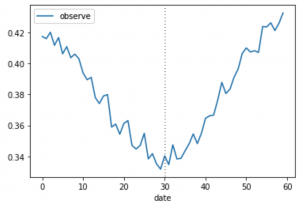
plt.show();

点線のdate=30で20%のユーザーにキャンペーンが適用されています。縦軸は、10,000ユーザーのその日あたりのアプリオープン回数です。
どうでしょうか？この測定結果を見て、キャンペーンの効果を正しく測定できそうでしょうか？「キャンペーンのおかげでV字回復している！」や「季節要因で回復するとは思っていたけれどこれほどまでとは…」など、様々な声が聞こえてきそうです。

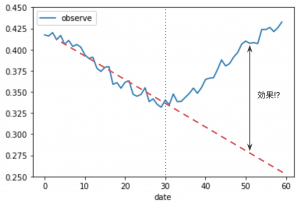
ここで、現場でよく行われる前後比較の分析をしてみたらどうなるか、試してみましょう。解析結果は、「0 ~ 30日でのトレンドがこのまま続くとすると、赤い点線のようなダウントレンドだったはずのものが、キャンペーン適用により大幅に改善した」というものになります。果たしてこれはどれほど再現性がある分析なのでしょうか…？

3. 差の差分法（DID）

基本形

キャンペーンが適用されたユーザーと、適用されなかったユーザーの2群に分けることで効果を測定するのがDIDの手法でした。
まずはグラフ化することで、先ほど登場したV字回復グラフの中身を簡単に探ってみることにしましょう。

data_0 = user_history[user_history["treated"]==0].groupby("date")[["observe"]].mean()
data_0.reset_index(drop=False, inplace=True)
data_1 = user_history[user_history["treated"]==1].groupby("date")[["observe"]].mean()
data_1.reset_index(drop=False, inplace=True)

plt.plot(data_0["date"], data_0["observe"], label="control")
plt.plot(data_1["date"], data_1["observe"], label="treated")
plt.xlabel("date")
plt.legend()
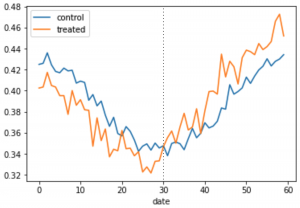
plt.show();

結果は以下のようになりました。キャンペーンが適用なかった群が青、適用された群がオレンジです。まず注目すべきは、オレンジのtreatedはキャンペーン適用前（0 ~ 30日）では1日あたりのアプリを開く回数は青のcontrolより低いですが、キャンペーン適用後（30 ~ 60日）で値が逆転している点でしょう。そして、先ほどまでV字回復と思っていたグラフの概形はキャンペーンを適用していない群でも確認でき、外的要因（今回は季節要因）だということもわかります。

では、キャンペーンにはどれほどの効果があったのか、推定してみましょう。DIDにおいて、効果は以下の式で表現できることを念頭において、計算を行うと、

did_result = user_history.groupby(["treated", "before_after"])[["observe"]].agg(["count","mean","var"])
display(did_result)

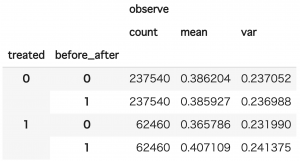
結果は、0.0416 (±0.0061)となりました。

アンチパターン

DIDは、その分析を成立させるため、平行トレンド仮定を置いていました。ここでは、その平行トレンドが成立しないケースでどのような推定を行ってしまうのか、確認してみましょう。

平行トレンドでないシチュエーションとして、データ生成時にアプリを開くかどうかの確率に、実はengagementも作用している場合を考えます。コードとしては、2. 実験データ作成の3つ目のコードブロック21行目を以下のように書き換えます。

user_history["prob"] = np.clip(user_history["eng"] * user_history["seasonal"] - user_history["date"] * user_history["eng_baseline"]*0.2/L, 0, 1)

少し恣意的と思われるかもしれませんが、上記のコードに置き換えて生成したデータを元に作成したグラフに、キャンペーン適用前の2群のトレンドラインを示してみました。

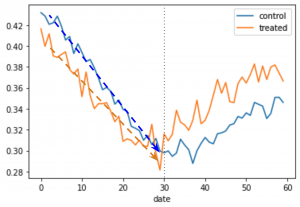
このケースではengagementが低いほど（つまりオレンジのラインほど）、傾きの絶対値が小さくなるようにデータを作成しているので、キャンペーン適用前後でオレンジ側に有利なトレンドとなっています。この時の結果は、0.0502 (±0.0030)となり、見た目ではちょっとの平行トレンドのズレが、測定時にキャンペーン適用効果を過大に推定してしまうことがわかりました。

4. IPW推定

基本形

キャンペーンが適用されるかどうかを何らかのモデルで表現し（= 傾向スコア）、その逆重み付けで効果を推定するのがIPW推定でした。以下の式が効果の推定量となるので、これまで作成してきたデータに当てはめてみましょう。

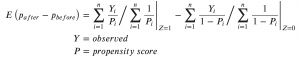
一つ足りないパーツとして、ユーザーごとにキャンペーンが適用されるかどうかの傾向スコアを作成しなければなりません。
次のコードでは、上記で作成したx1 ~ x4を共変量として、statsmodelsでロジスティック回帰モデルのパラメータを推定した後、作成された傾向スコアをもとに効果の推定と、標準誤差を求めています。標準誤差は、残差の重み付け平方和を取る形での実装となります。

import statsmodels.api as sm

# ロジスティック回帰モデルの作成
df = user_feat[["x1","x2","x3","x4","treated"]].copy()
df = sm.add_constant(df)

logit_mod = sm.Logit(df[["treated"]], df[["const","x1","x2","x3","x4"]], family=sm.families.Gamma())
logit_res = logit_mod.fit(method="newton")
print(logit_res.summary())


# モデルの出力結果を傾向スコアとしてテーブル化
res = pd.DataFrame()
res["user_id"] = user_feat["user_id"]
res["propensity"] = logit_mod.endog - logit_res.resid_response

ipw_data = user_history[["user_id", "before_after", "treated", "observe"]].copy()
ipw_data = ipw_data[ipw_data["before_after"]==1]
ipw_data = pd.merge(ipw_data, res, on="user_id", how="inner")

# 定義に従ってIPW推定量を計算
cond_e1 = ipw_data["treated"]==1
E_1 = ((1 / ipw_data.loc[cond_e1, "propensity"])*ipw_data.loc[cond_e1, "observe"]).sum() / (1 / ipw_data.loc[cond_e1, "propensity"]).sum()

cond_e0 = ipw_data["treated"]==0
E_0 = ((1 / (1 - ipw_data.loc[cond_e0, "propensity"]))*ipw_data.loc[cond_e0, "observe"]).sum() / (1 / (1 - ipw_data.loc[cond_e0, "propensity"])).sum()

ipw_data["residual"] = 0
ipw_data.loc[ipw_data["observe"]==1, "square_error"] = ipw_data["propensity"] * np.power(ipw_data["observe"] - E_1, 2)
ipw_data.loc[ipw_data["observe"]==0, "square_error"] = ipw_data["propensity"] * np.power(ipw_data["observe"] - E_0, 2)

se = np.sqrt(
    ipw_data.loc[ipw_data["observe"]==1, "square_error"].sum()/np.power((ipw_data.loc[ipw_data["observe"]==1, "propensity"]).sum(), 2) + 
    ipw_data.loc[ipw_data["observe"]==0, "square_error"].sum()/np.power((ipw_data.loc[ipw_data["observe"]==0, "propensity"]).sum(), 2)
    )

print(E_1 - E_0)
print(se * 1.96)

結果は、0.0433 (±0.0083)となりました。DIDの時と同様に真のキャンペーン効果を推定できていることがわかります。

アンチパターン

IPW推定では傾向スコアが正しく作成できるかどうかが、バイアス除去のキモになります。モデルのAUCや共変量の分布でその”正しさ”を評価することになるのですが、DIDにおいて平行トレンド仮定を確かめるためにこれだけチェックしておけば大丈夫という手法がないように、傾向スコアが正しく作成できているかを評価する確立された手法はありません。
そこでこのアンチパターンでは、x4を脱落変数とし、x1 ~ x3のみを利用してロジスティック回帰モデルを作成してみるとどのような推定結果となるのかを試してみます。

実装は非常に簡単で、上記コードの7行目を以下に変更するだけです。

logit_mod = sm.Logit(df[["treated"]], df[["const","x1","x2","x3"]], family=sm.families.Gamma())

推定結果は0.0394 (±0.0017)となり、真のキャンペーン効果からズレが生じてしまっています。

5. 最後に

今回は、キャンペーンデータを模擬的に生成し、その効果を因果推論の手法で測定しました。特にアンチパターンはビジネスの現場で自分が陥らないようにという筆者自身への戒めも込めてまとめました。今後も、データをビジネスの成功につなげる武器としての因果推論を、現場にどんどん取り入れていきたいと思います！

次世代システム研究室では、データサイエンティストとビッグデータ解析プラットホームの設計・開発を行うアーキテクトを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。
一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。