セルオートマトン
こんにちは。次世代システム研究室のJK（男）です。今回はセルオートマトンについて書いていきます。
セルオートマトンは古くから研究されているテーマです。古い技術＝時代遅れとは限りませんし、温故知新の精神で学んでみました。セルオートマトンの説明は1章でします。個人的にはセルオートマトンの「均一性・局所性」が面白いと思っています。非常に単純なルールが局所的に適用されるだけで全体のパターン形成されますが、色々な場面で応用ができそうですね。ここでは3章で金融への応用（のさわり）について書きます。今回のブログの内容はこちらの書籍の8章を基に書いています。
1. 1次元セルオートマトンによるパターン生成
1次元セルオートマトンとは、一次元の正方形（セル）が並んだものです。各セルは状態があります（0, 1..とか）。で、1ステップ毎にセルの状態が更新されていきます（0→1, 0→0, ..etc）。更新方法は、現在の自分・近傍のセルの状態を基に特定のルールが適用されます。ここでは一番な簡単なケースを考えます。すなわちセルの状態は2つ（0/1）、ルールは該当セルとその両隣の状態から決まります。ルールは、とり得るパターン=2^3=8通りについて、該当セルが0になるか1になるかを決めればOKです。たとえば以下のようなルールが考えられますね。
上記の例だと、左端は該当セル・両隣の状態が黒=1だった場合、次のステップで該当セルは1になるということです。左から二番目は、該当セルと左隣が1で右隣が0の場合は、次のステップで該当セルは0になります。例を見ればわかるように8状態に対して、該当セルが0/1を取るかは任意に決められるので、全部で2^8 = 256通りのルールを作ることができます。下図はそのうち6つのルールで作られたセルオートマトンのプロットです。最初のセルの状態はランダムに0/1にしています。
通常、1次元セルオートマトンでは次のステップの状態が前の状態のすぐ下にプロットされます。上図でいうと、一番上の列が最も古い状態で、それが1ステップ更新された状態が次の列にプロットされ、さらにそれが更新され、、と続いています。長さ150のセルを150回更新しています。パターンのようなものが見えていますね。
ここで面白いのは、上記のような非常に単純なルールからこのような面白いパターンが生成されることです。特に面白いと思うのは以下の2点です。
- 局所性：各セルは近傍のセルの状態しか知らない。
- 均一性：特別なセルは存在しない。全てのセルに同じルールが適用される。
さらに面白いことにセルオートマトンと似たパターンが、自然界にいる貝の模様に見られるということです。貝殻は1次元オートマトンのように、端から一層ずつ伸びていくように作られるので、似たパターンになるのは偶然ではなく実際にこのような仕組みで作成されている可能性があります。ただし「上記ルールで再現できる」=「実際に同じ仕組みで生成されている」ではないことには注意してください。再現できることは必要条件ですが十分条件ではないですね（以下の章の例でも同じです）。
2. 2次元セルオートマトンによるパターン生成
この章では2次元セルオートマトンについて考えます。単純に1次元のセルを2次元に拡張しただけで、セルは直線から長方形の分布に変わります。すぐ隣のセルは1次元では2つでしたが、2次元の場合は4/8になります。更新方法は1次元と同じく、自分と近傍のセルの状態に応じて次のステップのセル状態が決まります。近傍のセルが増えた分だけ（とり得る）ルールの数は増えますが考え方は同じです。ここでは1章より少し複雑なルールを考えます。
- 100 x 100の2次元セル
- セルのとり得る状態は２つ（0/1）
- 3つ隣のセルの状態まで考慮します。考慮の条件は、
- v := c_0 + c_1 + p0 * c_2 + p1 * c_3
- c_Nは, 該当セルからNの距離にあるセルの状態
- p0, p1は可変（パラメータ）
- v>=0のとき、該当セルの状態を1に更新、v<0のとき0に更新。
4つのパラメータセットについて図示しています。左から順に(p0, p1) = (-0.4, -0.4), (-0.3, -0.3), (-0.2, -0.2), (-0.3, -0.1)です。1次元の場合と異なり過去の履歴は描かず、最終状態のみプロットしています。最初はランダムな状態から始めて、10ステップ後の状態です。面白い事に生成されたパターンは動物の模様（たとえばチーター、キリン）に似ていますね。動物の模様は実際は化学作用の複雑な作用で作られていると考えられますが、面白い事に細かい仕組みがわからなくても、単純な相互作用のルールを定義することでパターン生成が可能なことがわかります。
3. 金融への応用（のさわり）
1-2章では動物の模様生成などについて書きましたが、もちろん他の応用も考えられます。ここでは金融への応用について検討するため、とても単純化した株の売買市場について考えます。ルールは以下のようにします。- 1次元セルオートマトンのシステムを使う。
- 複数の銘柄を考える。1銘柄=1セル。
- 値段の上下をセルの状態とする。状態は2つ（値段が上がる=1, 下がる=0）。
- 該当セルは以下のルールで更新される。
- （自セルの状態に関わらず）両隣がどちらも0か、どちらも1だった場合0
- （自セルの状態に関わらず）両隣が0と1だった場合1
縦軸が時系列に対応して、各列が1銘柄分の値段上下記録になります。以下の図では、連続する3銘柄(A0, A1, A2)の値段の時系列をプロットしています。ここで簡単のため、値段の上下幅は一定と仮定しています。
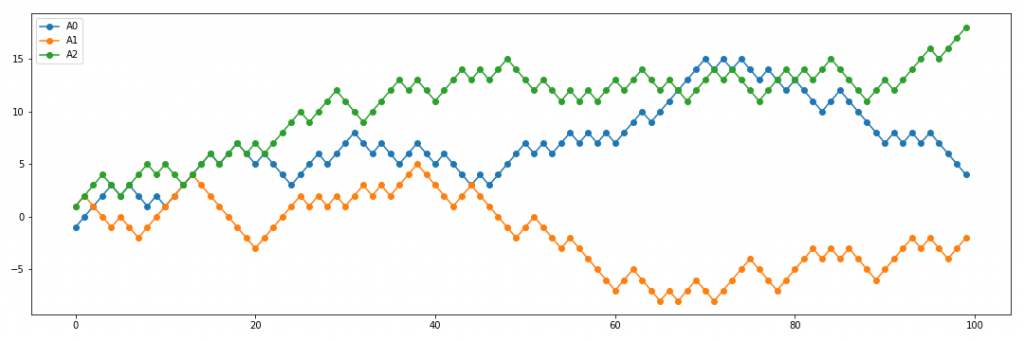
図を見れば分かる通り、全ての銘柄に（全く同じ）単純なルールを適用して売買しているだけにも関わらず、値段の動きはランダムなように見えます。上記はかなり単純化した場合なので、実際のマーケットはより複雑な動きになるでしょう。ここでのポイントは「（疑似）ランダム性は、ルールにランダム性を追加しなくても、多数のセル（=参加者）の相互作用だけで生成される」というところです。金融市場の値動きを予想するのがいかに難しいかがよくわかります。
まとめ
セルオートマトンは局所性・均一性のルールの下で相互作用して状態が更新されるシステムです。今回は1次元のケース、2次元のケースについてその振る舞いを確かめました。いずれの場合も、自然界の動物の模様に類似したパターンがあることから、自然界においてもこのような単純なルールで、複雑なパターンが生成されている可能性があります。最後に株の値動きの考察として、1次元のセルオートマトンを応用した例を書きました。多数のエージェントが局所的に相互作用する系には適用できるので、応用範囲は広いと思います。今後はもう少し深いところまで勉強していきたいと思っています。次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
