Is Attention All You Need? Part 1
Transformer を超える(?)新モデルS4

Is Attention All You Need?
HiPPO(Higher-order Polynomial Projection Operations)
1. HiPPO-LegS
LSSL(Linear State-Space Layers)
S4(Structured State Space Sequence)
Summary
Reference

Is Attention All You Need?

こんにちは、グループ研究開発本部・AI研究室のT.I.です。“Attention Is All You Need”といって発表されたTransformer(とAttention Layer)は、驚異的なAIの性能改善をもたらしました。以来、自然言語処理(NLP)などの分野では、従来のRecurrent Neural Network(RNN)ではなく、Transformer-based modelがデファクトスタンダードとなり、その延長線上に今日のChat-GPTなどの高性能AIが生まれました。 Transformer とその改良版については、これまでのBlogで何度も紹介してきました(Reformer, Vision Transformerほか)。最近のものを含めたTransformer系の発展については、こちらの解説Blog(30分で完全理解するTransformerの世界)が非常にコンパクトにまとまっていてわかりやすいです。

ただ、いつまでもTransformerの快進撃は果たして続くのでしょうか？“Attention Is All You Need”とは言いますが、Attentionの有用性に異論もあるそうです( “Attention is All You Need”は本当か調べる)。また、こちらのサイト(Is Attention All You Need?)では、「2027年までTransformer系のモデルがNLPでも主流であるか」という命題に対し賭けがされています(Mosaic MLの研究者は賛成、Hugging Faceの方は反対に投じています)。このサイトにアクセスすると期限までのカウントダウンと現在の状況をBertが教えてくれます。

Time Remaining:
http://www.isattentionallyouneed.com/より

ご覧のように現在~~(2023年3月末)~~時点では、“Attentionこそはすべて”の模様です。

そんな折に先日、Structured State Space (S4) sequence modelというモデルが発表されました。このモデルは長い入力シークエンスについてのベンチマークテストであるLong-Range Arenaにおいて、Transformer やその拡張モデルを圧倒するなど高い性能を発揮しました。あとで解説しますが、Path-X(Pathfinder-X)という他のモデルが失敗した長い入力長(16k!)に対する推論タスクに唯一成功している点が大きな成果です。

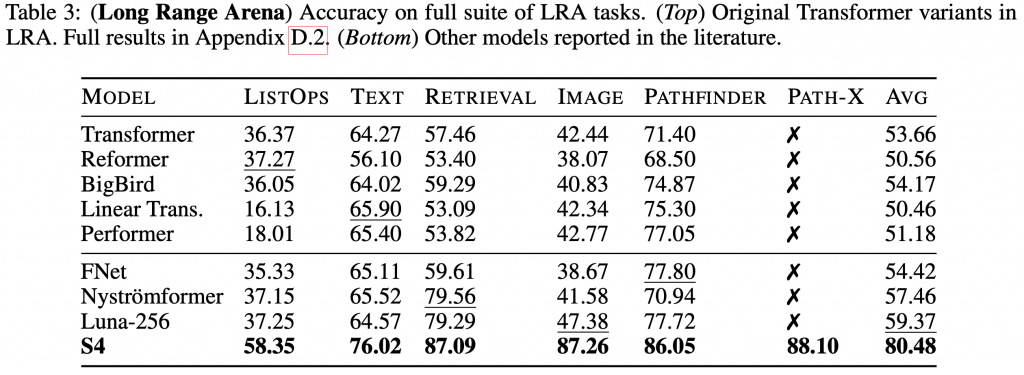
Long-Range ArenaのS4と他のモデルとの性能比較(表は、Efficiently Modeling Long Sequences with
Structured State Spacesより引用)

今回のBlogでは、興味深いこのS4について簡単に解説します。しかし、S4はLong-range dependence(LRD)を効率的に保持する方法を、数理的に追求し諸々の性質を駆使し計算の徹底的な効率化を達成するという、大変にハードルが高いモデルになっています。その理解には、HiPPOとLSSLというS4の前段階の研究が必須なので(少々、数式も多く大変ですが)順を追って解説します。 (注)私自身十分に消化しきれていない内容もあります。不正確な解説や誤解が含まれている可能性がありますので、興味を持った方は是非原著論文を読まれることを推奨します。

HiPPO(Higher-order Polynomial Projection Operations

最初は、HiPPO (Higher-order polynomial projection operations)です。これは NeurIPS 2020 で発表されました。時系列の入力を処理するモデルとしてRNNやLSTMなどのモデルがありますが、長い入力に対して記憶が十分に保持できない問題がありました。これに対して、入力信号をLegendre多項式で近似し改善するLMU(Legendre Memory Unit)が提案されていました。このLMUのアイデアを拡張したのが HiPPO です。

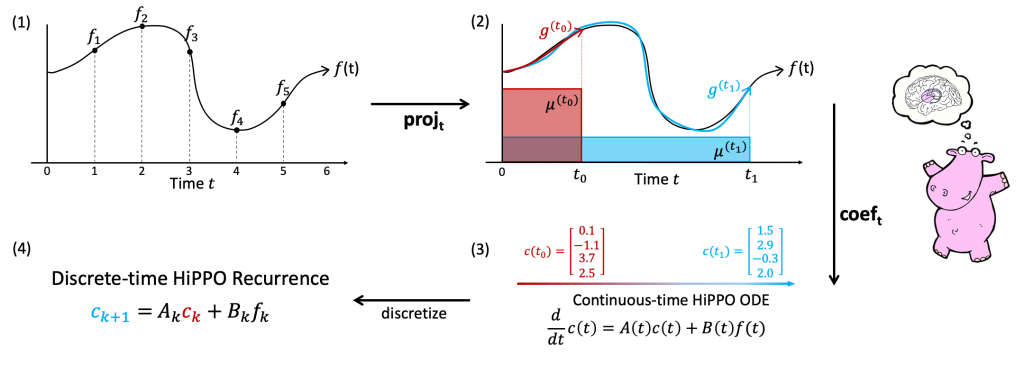
HiPPOの概略図(https://github.com/HazyResearch/state-spacesより引用)

この図は HiPPO の概念になります。順番を追って説明します。

入力される時系列データ $f(t) \in \mathbf{R}$ ($t \geq 0$) を考えます。時刻 $x$ までの履歴 $f_{\leq t} := f(x)|_{x \leq t}$を元に、その先の時刻の予測をします。すべての過去の履歴の記憶は難しいため情報の圧縮が必要です。HiPPO のアプローチでは、入力を多項式の和で近似しますが、その際に過去の重要度に相当する測度$\mu(t)$を導入します。

まず、時間に依存する測度($\mu(t))$を導入し、2つの関数の内積を以下で定義します。
$$
\langle f, g \rangle_\mu = \int_0^\infty f(x) g(x) d\mu(x)
$$
ノルムは以下のように与えられます。
$$
||f||_{L_2(\mu)} = \langle f, f \rangle_\mu^{1/2}
$$

$N$個の多項式基底を用いて入力$f$を近似します。
$$
f(t) \approx \sum c_n P_n(t)
$$
これは$N$-次元の部分空間$\mathcal{G}$に、入力の情報を圧縮することに対応します。そして、時刻$t$までの入力$f_{\leq t}$から、この多項式近似を順次更新します。それには、$g^{(t)} \in \mathcal{G}$に対して、 $||f_{\leq t} - g^{(t)} ||_{L_2(\mu(t))}$ を最小化すればよいです。これらの操作をそれぞれ

$\mathbf{proj}_t$: 時刻$t$までの入力 $f_{\leq t} := f(x)|_{x\leq t}$ を $g^{(t)} \in \mathcal{G}$
へ射影する操作($||f_{\leq t} - g^{(t)}||_{L_2(\mu(t))}$を最小化)
$\mathbf{coef}_t$: $g^{(t)} \in \mathcal{G}$の $N$ この係数 $c(t) \in \mathbf{R}^N$ を得る操作

とし、まとめて $f: \mathbf{R}_{\geq 0} \rightarrow \mathbf{R}$ を入力に、係数 $c: \mathbf{R}_{\geq 0} \rightarrow \mathbf{R}^N$を得る操作をhippoと呼びます。

$$
(\mathrm{hippo}(f))(t) = \mathrm{coef}_t(\mathrm{proj}_t(f))
$$

そして、重要な点が、係数$c(t)$の時間発展がODE(常微分方程式)
$$
\frac{d}{dt}c(t) = A(t) c(t) + B(t) f(t)
$$
を満たすことです。(ここで、$A(t) \in \mathbf{R}^{N\times N}$, $B(t) \in \mathbf{R}^{N\times 1}$)

更に時間を離散化すると、このODEは
$$
c_{k+1} = A_k c_k + B_k f_k
$$
のような形式に書き表せます。

HiPPO-LegS

HiPPO の操作の基本は上記の通りですが、具体的な計算では多項式基底や測度を与える必要があります。この論文では、Legendre 多項式を用いて、測度 $\mu^{(t)} = \frac{1}{t}I_{[0,t]}$ を採用したものを、 scaled Legendre measure(LegS) と呼びます。唐突に出てきましたが、Legendre多項式とは
$$
P_n(x) = \frac{1}{2^nn!}\frac{d^n}{dx^n}(x^2-1)^n
$$
で計算できる多項式($P_0(x)=1, P_1(x) = x, P_2(x) = \frac{1}{2}(3x^2-1), \dots$)で、以下の性質を満たすため多項式展開の基底として良い性質を持ちます。
$$
\int_{-1}^{1} P_m(x) P_n(x) dx = \frac{2}{2n+1}\delta_{mn}
$$

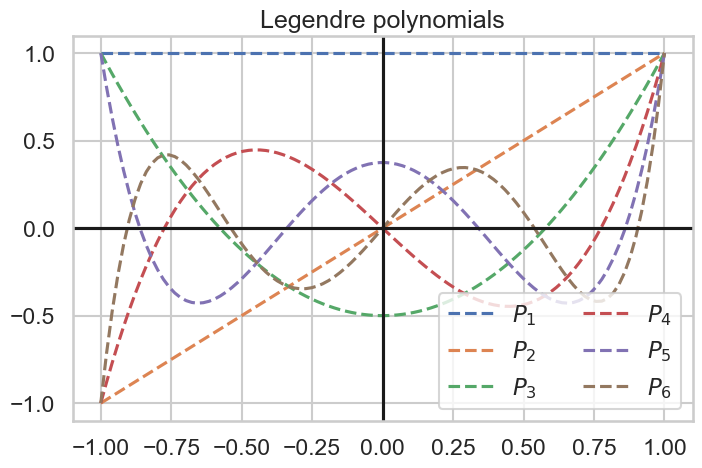
Legendre 多項式の例

この場合、HiPPO ODE
$$
\frac{d}{dt}c(t) = - \frac{1}{t} Ac(t) + \frac{1}{t} Bf(t)
$$
この行列$A$, $B$は以下の通り解析的に計算可能です。
$$
A_{nk} =
\begin{cases}
(2n+1)^{1/2}(2k+1)^{1/2} \quad &n > k \\
n+1 \quad &n = k \\
0 \quad &n < k \\ \end{cases}, \qquad B_n=(2n+1)^{1/2} $$ なお、この$A_{nk}$を後のS4の論文では、特にHiPPO Matrixと呼んでいます。
また、時間を離散化した場合$$ c_{k+1}=\left(1 - \frac{A}{k}\right) c_k + \frac{1}{k} Bf_k $$となります。これは、時間スケールの変換に対して不変であり、HiPPO-LegSは、時間の刻み幅$\Delta t$に依存しません。 HiPPO-LegSによる入力の近似の例が以下の図になります。直近の時刻のデータの再現性は高いですが、過去に遡るにつれて平均化した滑らかなものになっています。

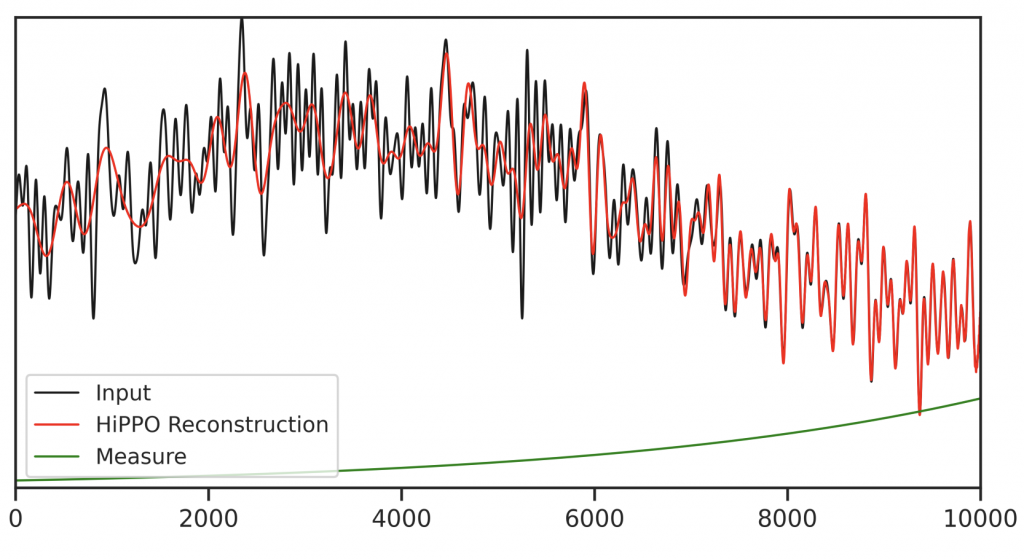
HiPPOによる入力近似の例。図は、How to Train Your HiPPO より引用

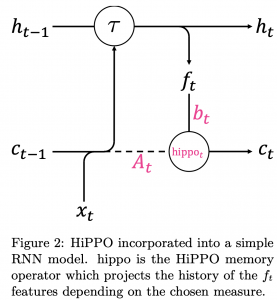
次のLSSLに進む前にHiPPOを使ったベンチマークの結果も紹介しておきます。モデルの構造としては以下の通りRNNモデルに、HiPPOの演算を組み込んだものになります。

HiPPOを組み込んだRNN回路。図はHiPPOから引用

以下の表は、HiPPO-LegSと他のモデルとpermuted MNIST (pMNIST)のスコアを比較です。pMNISTとは、MNIST(手書きの数字の画像を識別するテスト)の画像を pixel-by-pixel で並び替え判別するタスクです。HiPPO-LegSが、他のモデルよりも高いスコアを発揮しています。なお、詳細は割愛しましたが、HiPPO-LagT(LegT)とは、HiPPOでLaguerre(Legendre)多項式を採用し、scaled measureとは別の測度を採用したものです。HiPPOの性能は、これらの測度($\mu$)の選び方(過去の情報の重み)にも依存します。

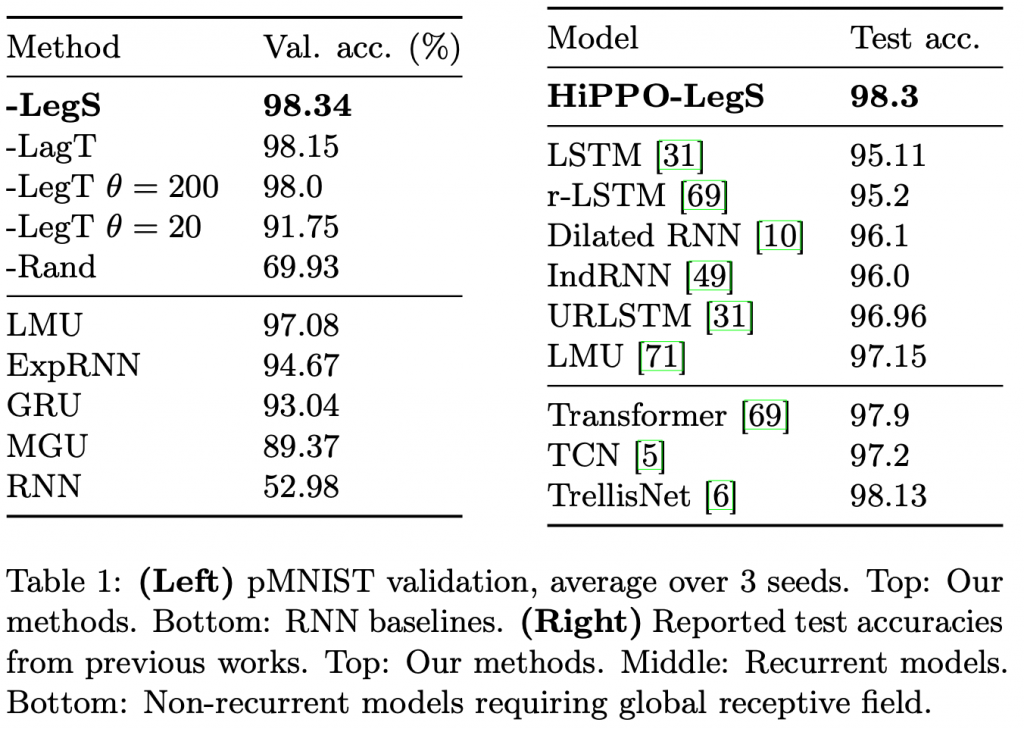
HiPPOと他のモデルの性能比較(表は、HiPPOより引用)

LSSL(Linear State-Space Layers)

HiPPOの拡張が、このLinear State-Space Layer(LSSL)です。LSSLはHiPPOのODEを拡張した以下の式で定義されます。

$$
\dot{x} = Ax + Bu
$$
$$
y = Cx + Du
$$

これは、写像$u_t \in \mathbf{R} \rightarrow y_t \in \mathbf{R}$ に、implicit state $x_t \in \mathbf{R}$を加えたもので、State Space model (SSM)になっています。この方程式は、以下のダイアグラムのように３種類の見方ができます。

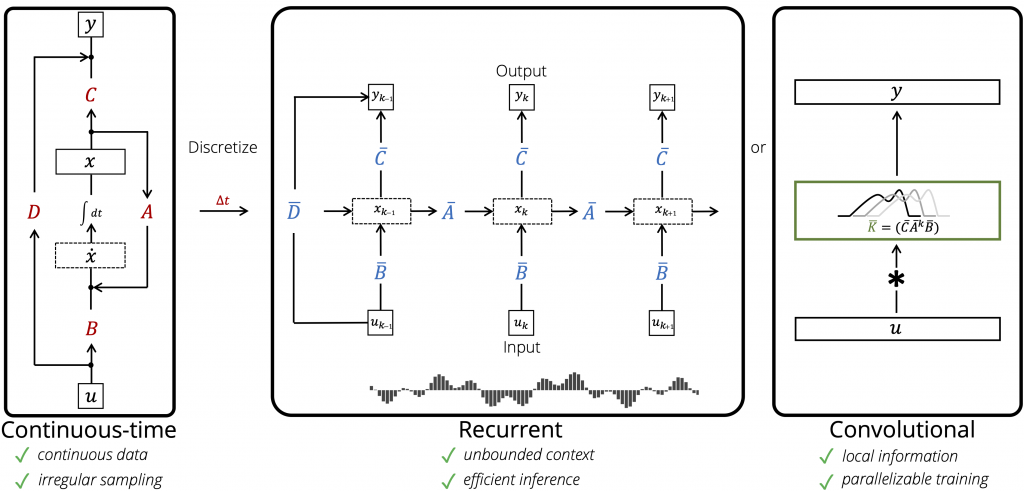
LSSLの概略図(図はhttps://github.com/HazyResearch/state-spacesより引用)

LSSLの式をダイアグラムで表現したものが左の図です。$x$の時間微分は入力$u$と$x$自身のフィードバックからなり、その積分が$x$になります。出力は入力$u$と$x$の線形和です。

さて、この連続時間での発展を時間ステップ$\Delta t$で離散化します。
$$
x(t + \varDelta t) = (I - \alpha \varDelta t \cdot A)^{-1}(I + (1 - \alpha)\varDelta t \cdot A)x(t) + \varDelta t(I -
\alpha \varDelta t \cdot A)^{-1}B\cdot u(t)
$$
となります。ここで、$\alpha$ は離散化の parameter です。離散化による補正後の係数をあらためて$\overline{A}$, $\overline{B}$とすると
$$
x_t = \overline{A} x_{t-1} + \overline{B} u_t, \quad y_t = C x_t + D u_t
$$
となります。これは、recurrent state $x_{t-1}$が過去の情報を伝える形式になっています。

特に$(A, B, \alpha) = (-1, 1, 1)$として、$\Delta t = \exp(z)$とすると
$$
x_t = (1- \sigma(z)) x_{t-1} + \sigma(z) u_t
$$
と、gated recurrence に帰着します($\sigma(z)$: sigmoid function)。つまり、LSSLはRNNを含むモデルとなっております。更に、十分に深く(無限)重ねたLSSLは、任意の非線形関数$f(t,x(t))$のODE($\dot{x}(t) = - x + f(t, x(t))$)を近似できる表現力を持つことも論文では証明しております。

なお、上記の時間発展ステップを書き下すと
$$
y_k = C(\overline{A})^k \overline{B}u_0 + C(\overline{A})^{k-1}\overline{B}u_1 + \cdots + C \overline{AB} u_{k-1} +
Du_k
$$
これは、convolution (畳み込み) 演算として、このように表現もできます。
$$y = \mathcal{K}_L(\overline{A}, \overline{B}, C) \ast u + Du$$
ここで、
$$
\mathcal{K}_L(A, B, C) = (CA^iB)_{i\in [L]} \in \mathbf{R}^L
= (CB, CAB, \dots, CA^{L-1}B)
$$
と定義します。

S4(Structured State Space Sequence)

さて、前置きが長くなりました。これでようやくStructured State Space sequence model (S4)を紹介できます。

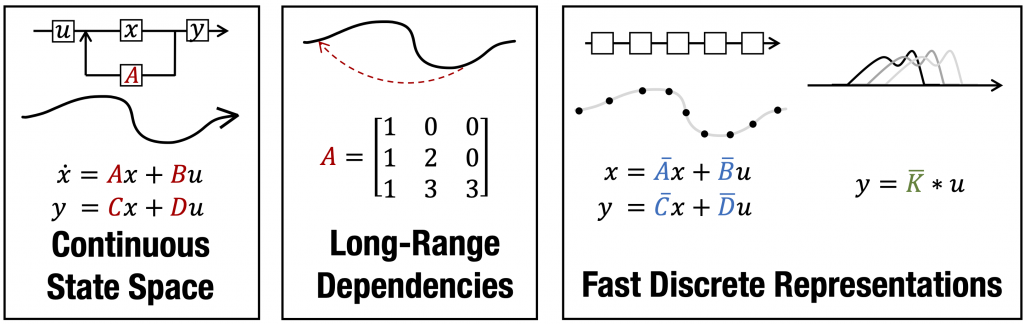
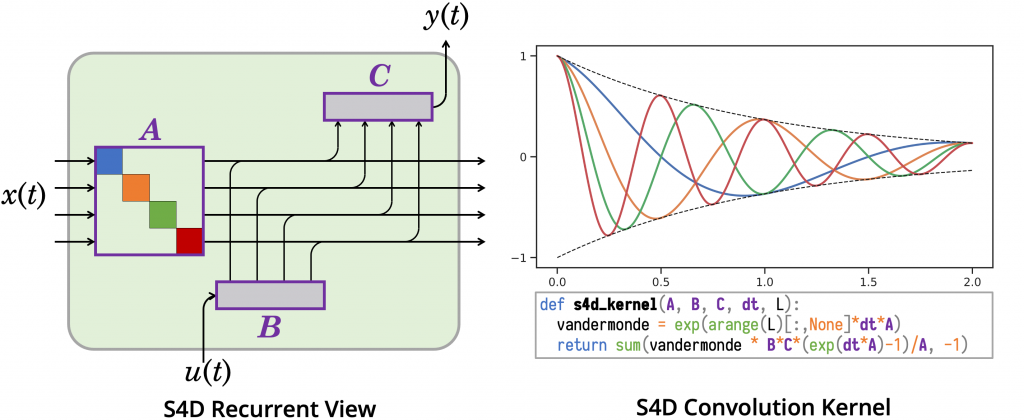
S4の概略図(https://github.com/HazyResearch/state-spacesより引用)

上図は、S4の概念図です。基本的なモデル構造はLSSLと同じですが、主なポイントは以下の２つです。

SSMのパラメーターをLong-Range Dependencies(LRD)を効率的に学習できるクラス(HiPPO matrix)に制限し学習
SSM Generating FunctionとCauchy Kernelを応用し高速な畳み込み演算処理を実現

SSM Generating Functions

LSSLと同様にSSMの計算をconvolution kernel(もしくは、filterとも呼びます)$\mathcal{K}_L$で評価しますが、実はこの計算に結構な演算($\sim\mathcal{O}(N^2L)$)とメモリー($\sim\mathcal{O}(NL)$)が必要です。その解決のために、SSMのGenerating functionを以下のように定義します。

$$
\hat{\mathcal{K}}_L(z; \overline{A}, \overline{B}, \overline{C}) \in \mathbf{C} := \sum_{i=0}^{L-1}
\overline{C}\overline{A}^i\overline{B}z^i
$$

これは$L$個の項の和ですが、級数の和 $1+x+x^2+\cdots + x^{n-1} = (1+x^n)/(1-x)$ を応用すれば、以下のようにも表現できます。
$$
\hat{K}_L(z) = \sum_{i=0}^{L-1}\overline{C}\overline{A}^i\overline{B}z^i
= \overline{C}(I - \overline{A}^Lz^L)(I - \overline{A}z)^{-1}\overline{B} = \widetilde{C}(I -
\overline{A}z)^{-1}\overline{B}
$$

なお、$z \in \Omega_L$ ($z^L = 1$)とします。つまり、行列の掛け算を繰り返して足し上げる必要はなく、一度の逆行列の計算で済みます。このGenerating functionを１のN乗根($z = \exp(2\pi i k/L)$ for $k=0, 1, \dots, L-1$)で評価し、逆フーリエ変換により元々の計算に帰着します。

Diagonal Case and Cauchy Kernel

Generating Functionを利用して、計算がだいぶ簡単にはなりました。さらに、効率化を進めます。一旦、行列$A$が対格行列($A=\Lambda$)の場合を考えますと、逆行列は対角成分の逆の和として計算できます。
$$
\hat{K}_\Lambda(z)
= c(z) \sum_i \frac{\widetilde{C}_i B_i}{g(z) - \Lambda_i} = c(z) \cdot k_{z,\Lambda}(\widetilde{C}, B)
$$
この$c(z)$、$g(z)$は$z$の関数です。また、$K_{ij} = 1/(\omega_i - \lambda_j)$の形式で表現されるものをCauchy kernelと呼び、その行列計算は効率的に実行可能です($M \times N$行列に対して単純には、$\mathcal{O}(MN)$のところ$\mathcal{O}(M+N)\log^2(M+N)$)。

Diagonal Plus Low-Rank

しかし、$A$が対角成分のみというのは、強い条件なので少々緩和して、Diagonal Plus Low-Rank(DPLR)であると仮定します。これは
$$
A = \Lambda - PQ^\ast
$$
ここで、$\Lambda$は対格行列、$P, Q \in \mathcal{C}^{N\times 1}$で表される行列のことです。

この場合、Woodbury恒等式
$$
\left(\Lambda + PQ^\ast \right)^{-1} = \Lambda^{-1} - \Lambda^{-1}P(1+Q^\ast \Lambda^{-1}P)^{-1}Q^\ast\Lambda^{-1}
$$
を利用すると、対角成分のみ処理に帰着できるので、最終的にgenerating functionは
$$
\hat{K}_{\mathrm{DPLR}}(z) = c(z)
\left[k_{z,\Lambda}(\widetilde{C}, B) - k_{z,\Lambda}(\widetilde{C}, P)
(1 + k_{z,\Lambda}(Q^\ast, P))^{-1}k_{z,\Lambda}(Q^\ast, B) \right]
$$
と、４つのCauchy kernelの組み合わせで計算できます。

上記の仮定ですが、HiPPO行列は、Normal Plus Low-Rank($A = V\Lambda V^\ast - PQ^T$、ここで、$V \in \mathbf{C}^{N\times N}$で、$P,Q \in \mathbf{R}^{N \times r}$)という性質を満たします。更に、それを変形させるとDPLRの形式に変換できます。

長期の記憶(LRD)をどのように保存するのか？という考えで考案されたHiPPOから、LSSLでの拡張と、LSSLの課題を改善するための工夫を経てS4では、最終的にコストは $\mathcal{O}(N+L)$ 程度まで改善できました。

S4を実際に動かしてみるならhttps://github.com/HazyResearch/state-spacesのリポジトリを利用すると良いでしょう。また、「The Annotated S4」では、Pythonのjax libraryを利用して具体的な計算式をステップごとの解説と実装がありとても参考になります。

Performance of S4

ひたすら数式が出て疲れたので、最後にS4のパフォーマンスを紹介します。

まずは、S4とLSSLの比較です。

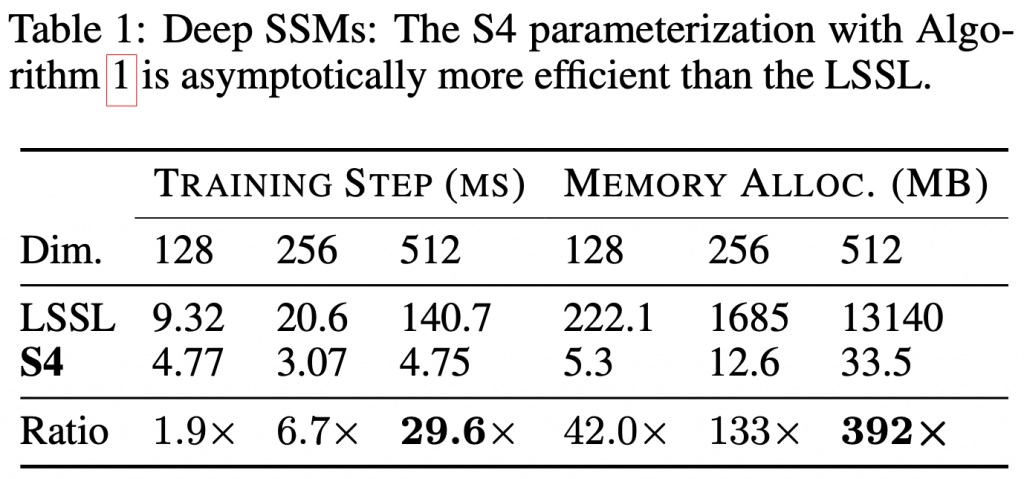
LSSLとS4との実行時間・メモリの比較(表はS4より引用)

S4では、LSSLから数理的な改善を凝らし、訓練ステップや必要なメモリが飛躍的に高速・効率化しました。その性能差はモデルが大きくなるほど広がり、512次元の場合では、訓練ステップは約30倍、メモリとしては400倍近い改善となります。

次に、最初にも紹介した Long Range Arena (LRA) の各種ベンチマークの Transformer とその改良版の結果の比較です。

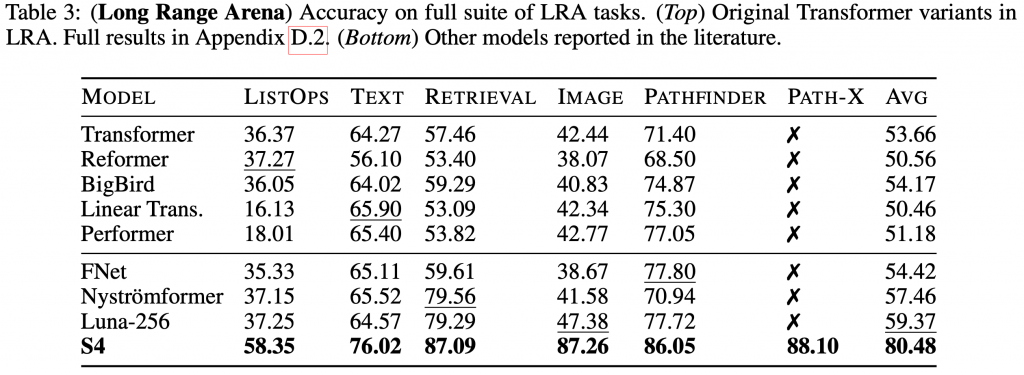
Long-Range Arena のS4およびTransformer系モデルのベンチマーク結果(表はS4より引用)

S4では、全タスクにおいて圧倒的な差をつけています。他のモデルでは解けなかった、Path-X(Pathfinder-X)のタスクをパスすることが特筆すべき点です。Pathfinder-Xとは、$128 \times 128$の画像データを$128 \times 128 = 16,384$の長さのシークエンスとして入力し、２つの点がつながっているのかを判定する課題です。これは、元々の$32 \times 32$の画像から２つの点の連結を判定するPathfinderの拡張です。

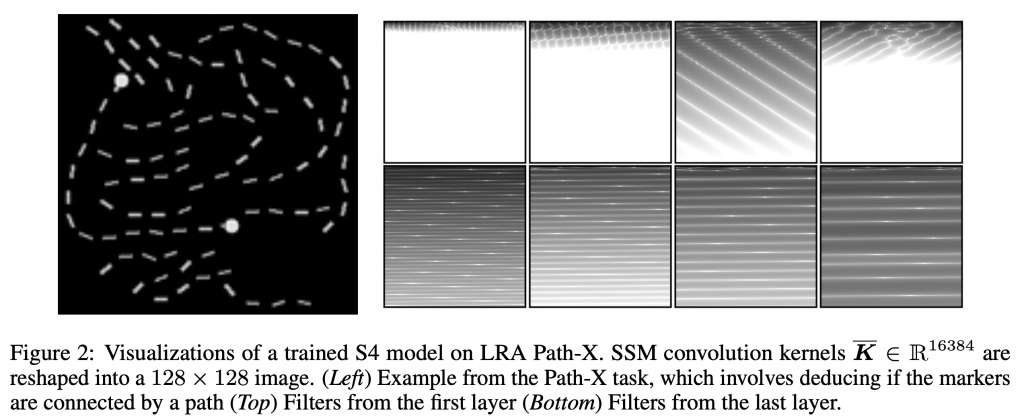
(左)
Path-X(Pathfinder-X)の課題の例 (右) S4のfilterの可視化結果 (図はS4より引用)

この図の左が、Path-Xの画像データで、右はS4の convolutional kernel $\overline{K}$ を $128 \times 128$ に変形して可視化したものです。低い層では、局所的な特徴しか抽出しませんが、高い層になるにつれ、大域的な特徴を抽出することを示唆しています。

Summary

今回のBlogでは、LLM などでデファクトスタンダードとなっている Transformer ではなく、Long-Range Dependenceを数理的に深く考察し得られたS4(Structured State Space sequence model)を解説しました。非常に長いシークエンスの学習に強みのあるモデルでTransformerを超える可能性を秘めており、今後の発展に期待しています。機械学習の論文を読んでいると従来のネットワークを修正し性能改善を目指す研究はよく見かけますが、今回のように数式でガリガリと力業(数学)で攻める形式で読んで非常に面白かったです。また、S4を発展させた研究も着実に進捗しております。S4を音声生成へ応用した SaShiMi(論文を読んでも何をどう略してSaShiMiになっているのか不明ですが、表題“It's Raw! Audio Generation with State-Space Models”や、 SaShiMi Sound Examplesなどを読むと、まさに刺身が由来のようです)や、S4のSSMを更に改善させたS4D などがあります。

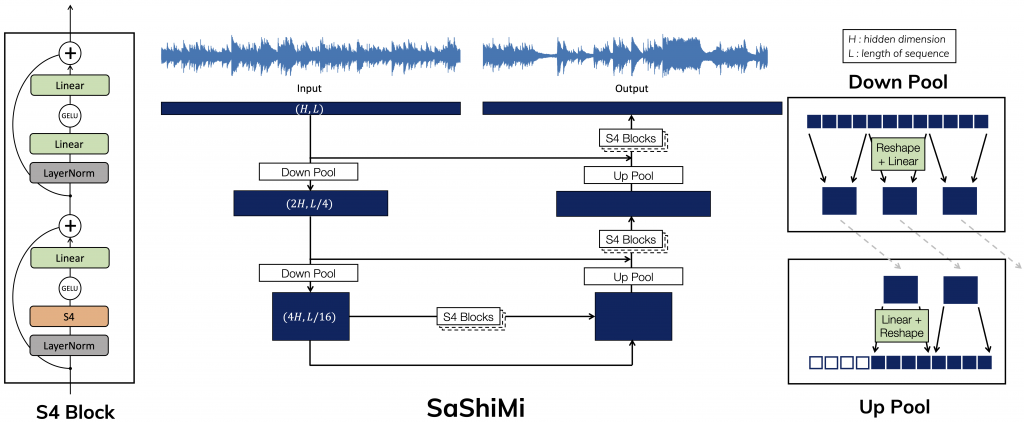
SaShiMi(https://github.com/HazyResearch/state-spacesより引用)

S4D(https://github.com/HazyResearch/state-spacesより引用)

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。

Reference

Attention is All You Need : Transformer(Attention)を提唱した論文(表題がとにかく強いです)
Is Attention All You Need? : Transformer(Attention)が、2027までNLPの主流であるか賭けていますが、現在のところAttentionは必要な様子です
30分で完全理解するTransformerの世界 : Transformerとその発展させたモデルまとめられています
Efficient Modeling Long Sequences with Structured State Spaces (ICLR 2022 Oral) : S4の原著論文
Legendre memory units: Continuous-time representation in recurrent neural networks : HiPPOで採用されているLegendre多項式で入力を近似する手法を考案した論文
Long-Range Arena (LRA) benchmark : Transformer 系のモデルの性能を評価するためのベンチマークテスト
HiPPO: Recurrent Memory with Optimal Polynomial Projections (NeurIPS 2020 Spotlight) : HiPPOの論文
How to Train Your HiPPO: State Space Models with Generalized Orthogonal Basis Projection : S4 で、HiPPOのスキーム依存性などを議論した論文
Combining Recurrent, Convolutional, and Continuous-time Models with the Linear State Space Layer (NeurIPS 2021) : LSSLの論文
HazyResearch/state-spaces : S4 などのオリジナル実装のレポジトリ
The Annotated S4 : S4の解説記事、特に具体的な数式やcodeもステップごとに解説されていて分かりやすいです
HiPPO/S4解説 : HiPPOからLSSL, S4への発展が数式と共に詳しく解説されている
時系列モデリング手法HiPPOを読み解く(1)
: HiPPOの詳細な解説
時系列モデリング手法HiPPOを読み解く(2) : 同上
It's Raw! Audio Generation with State-Space Models : S4を音声生成に応用したSaShiMiの論文ですが、SaShiMiの命名由来は特に触れられていない
SaShiMi Sound Examples : SaShiMiで合成した音声を聞くことができます
On the Parameterization and Initialization of Diagonal State Space Models : S4を改良したS4Dの論文

Is Attention All You Need? Part 1
Transformer を超える(?)新モデルS4

Is Attention All You Need?