こんにちは。次世代システム研究室のC.Zです。よろしくお願いします。

本文はベイズ統計学手法のdeep learning応用について、基本な理論を紹介し、FX予測の実装を実践しみます。

なぜneural networkもベイズ統計を使うか

統計学において、パラーメータの推定には大きく分けると、二つの手法があります。

• 伝統的な統計学　→　Maximum Likelihood Estimation (MLE)

⇔　点推定

• ベイズ統計学　→　Maximum a Posteriori (MAP)

⇔　確率分布の推定

伝統的な統計学には、幾つの欠点があります。

例えば、データが足りない場合や訓練データに極端データは多く存在した場合、過学習が非常に発生しやすいです。また、local optimumにかかりやすいので、特に初期値の設定と最適化も非常に困難です。

それに、一般な統計分野だけではなく、deep learningの分野でも似たような現象があります。

確率論の視点からすると、標準neural networkのweightsとbiasを最適化するため、実質上はMLEの利用と相当します（cost functionの変形）。ここから質問が再度生じました。

→　なぜMLE？なぜ点推定？推定値の不確実性を完全に無視してよいか？

結局的に、実務上でもneural networkの過学習が確かに大きな課題になります。

上記過学習問題を部分的に解決するための手法として、regularizationがよく使われています。

⇔　近似的にMAEになるが、確率論の視点からすると「正しくない」方法である

相対的に、「正しい方法」はベイズ統計のMAEです（本当のposterior推定）。

伝統的な統計学と違って、一つ確定な値を点推定することでなく、ベイズ統計ではパラーメータを確率変数と見なし、パラーメータの確率分布を推定することになります。

代表的な手法として、下記セクションで紹介するMarkov chain Monte Carlo methods(MCMC)とVariational Inference(VI)があります。

ベイズの定理と推定法

ベイズ推定

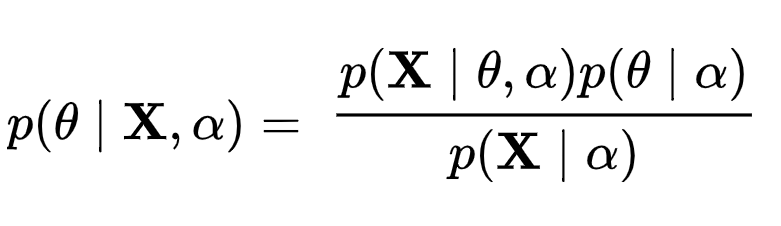
ここでは、

はサンプルの観察値、は観察値分布のパラーメータ、はの分布のハイパラーメータ

⇔

：事前分布(prior distribution)

：事後分布(posterior distribution)

：尤度(likelihood)

ベイズ予測

ここにも、新しい観察値に対する予測は、確定な点推定パラーメータを使うことではなく、全ての推定確率分布を利用しました。

Markov chain Monte Carlo methods(MCMC)

上記のベイズ推定式において、事前分布（人間選ぶ）と尤度（サンプルの結合分布）は得やすいですが、はに依存しないので、計算は難しいです。

なお、は定数なので、を正規化ための定数と見なすことができます。

→　を無視する

=>　
この近似式はMCMCの手法です。

しかし、MCMCは精確に事後分布に近似することが可能ですが、計算コストが非常に高いので、特に性能面を考慮すると、VIという手法が代わり挙げられました。

Variational inference (VI)

詳細について略しますが、基本なアイディアを紹介します。

→　事後分布を直接に求めることではなく、もう一つ別の分布qを導入し、近似分布qと事後分布pの距離をなるべく近づけるように調整します。

⇔


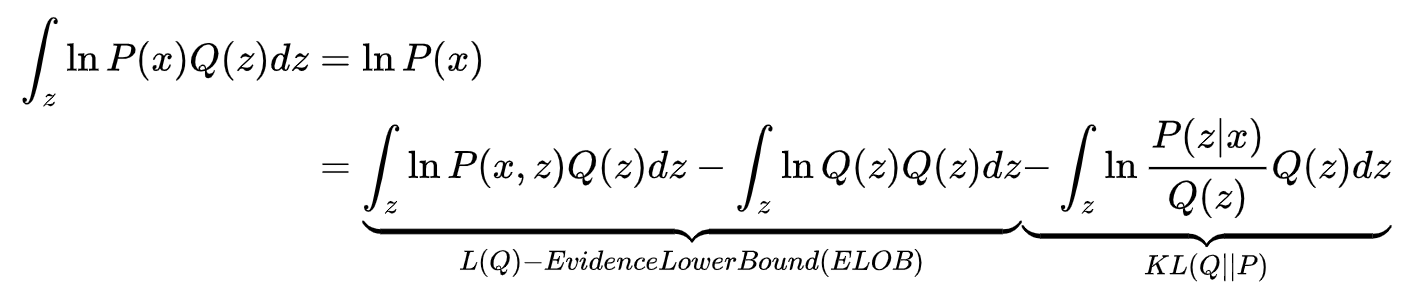
ここでは、

は事後分布pと類似分布qの近似度指標　→　０であれば、pとqが一番類似

しかし、事後分布pは分からないので、KLも計算できないです。

一方、上記式からわかるように、argmin(KL)＝argmax(ELOB)があり、ELOBの上限値が算出できるので（略）、最後安定的なq分布が得られます。

ベイズ推定法の実装ルート

確率的なプログラミング言語 → stan

ここは一番主流的な確率的なプログラミング言語であるstanを紹介します。

stanは沢山な確率分布関数や尤度計算に特定した関数が用意され、モデルを共通なプログラミング言語で記述し、データを渡すだけでよいです。

当然、上記紹介したMCMCやADVIが簡単に利用できます。

⇔


R、Python、Matlabなど向けのinterfaceがもちろんありますが、特にRならbrmsなどの強化packageもあり、モデルの記述でもプロットでも非常に有力で使いやすいです。

但し、近年deep learningの流行につれて、stanはそれとの統合性問題が出て、また性能上も他社に劣るケースが多く、将来の開発に懸念が生じました。

ほかのベイズ推定ツール

Stan以外、Tensorflow Probability、Edwardなどのpython moduleがあります。

Tensorflow Probabilityはtensorflow生態の製品なので、tensorflowとの統合性がいいですが、layerの種類まだ少ないのは欠点です。

Edwardも有名な統計学学者より開発され、沢山なdeep learningのlayersが既に実装され、直接利用できるため使いやすいです。

また、pytorch生態もblitzという開発中packageがあり、neural networkにベイズlayersがシンプルに追加されることができます。

 

ベイズdeep learningを使ってFXを予測してみる

ベイズ推定とLong short-term memory(LSTM)に組み合わせ、USD/JPYレートの予測をしてみました。

データ

https://www.histdata.com/download-free-forex-historical-data/?/metatrader/1-minute-bar-quotes/USDJPY

2020/05の1 minute barデータ

モデル

標準なLSTM構造

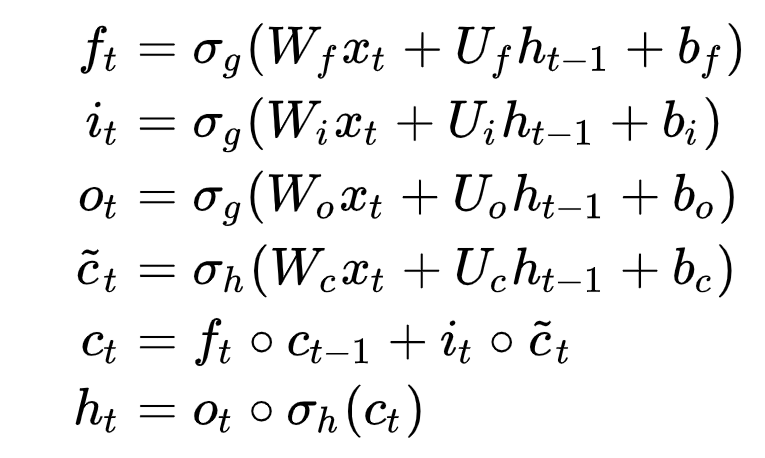
ベイズ推定

• VI法により推定します
• 事前分布：一般的な無情報分布事前分布　→　正規分布

=>

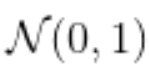
• 推定　→　過去30分のデータを学習し、次の1分のレートを予測する
• 予測　→　過去30分のデータを学習し、次の3分のレートを予測する

実装

今回は、LSTMのlayer実装があるpytorch生態のpackageであるblitzを利用しました。

https://github.com/piEsposito/blitz-bayesian-deep-learning

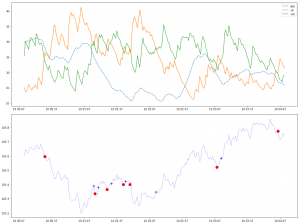
結果

Loss (20 epoch)

各epoch最後のiterationの値


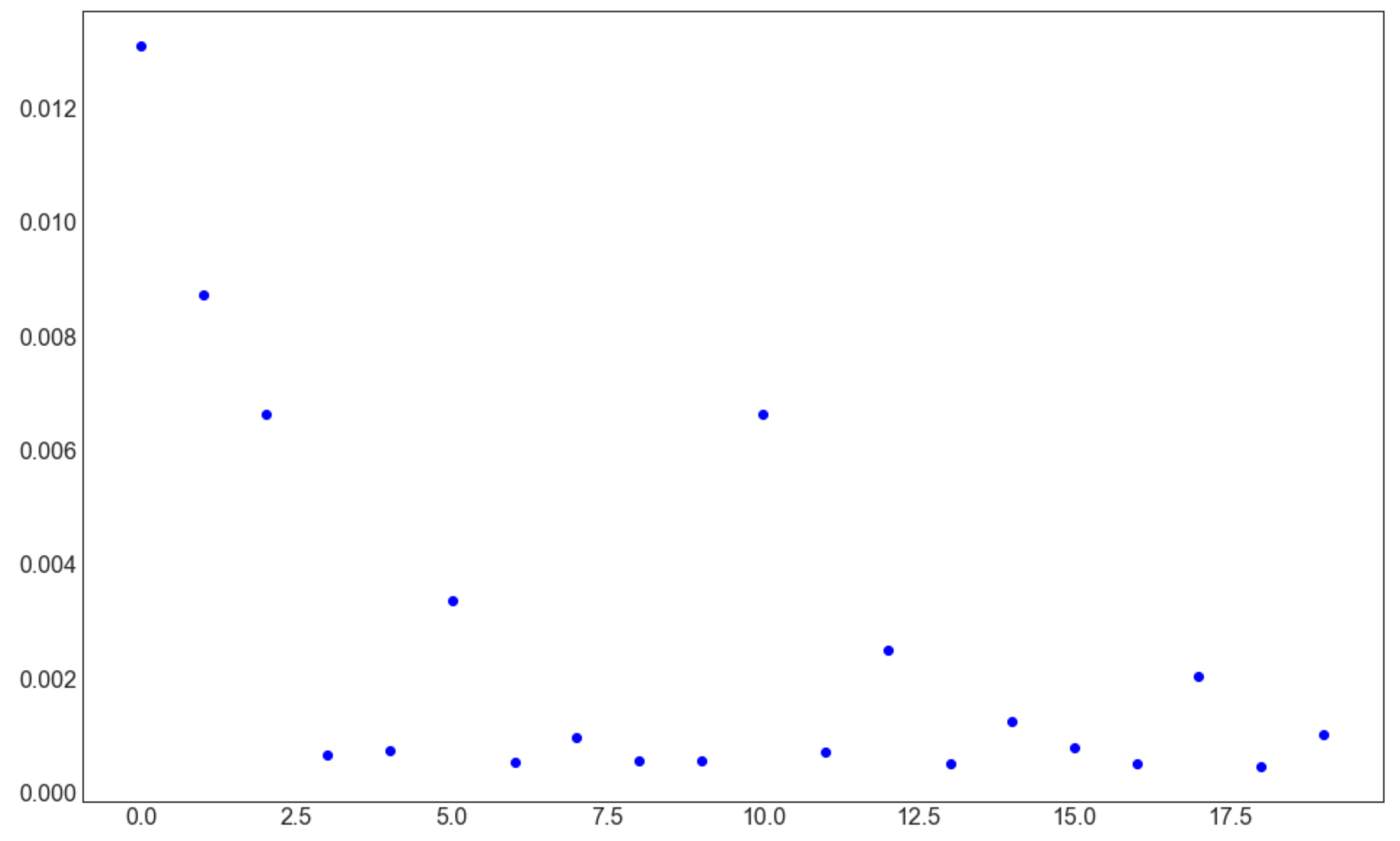
＝＞　収束が見える

90%信頼空間

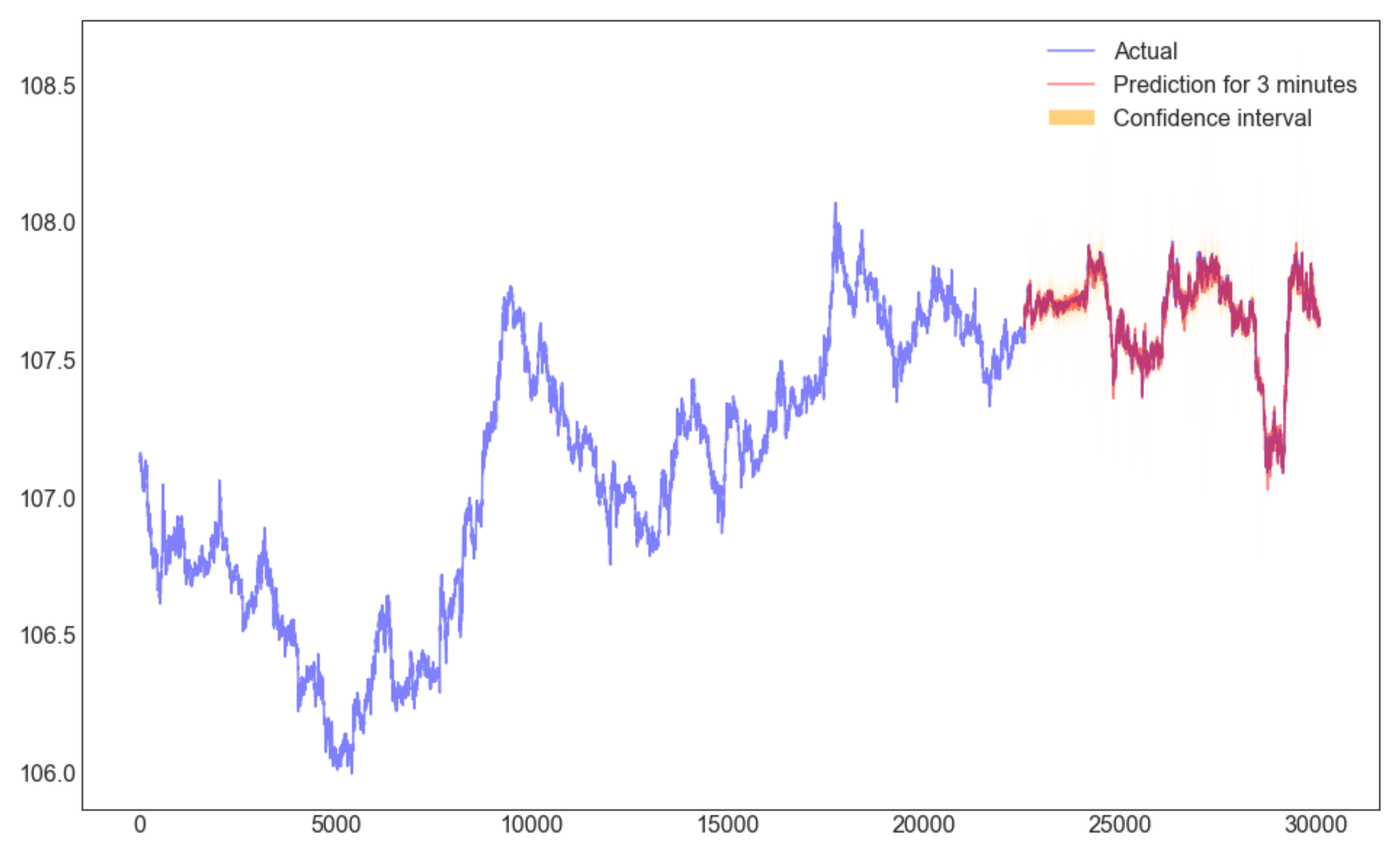
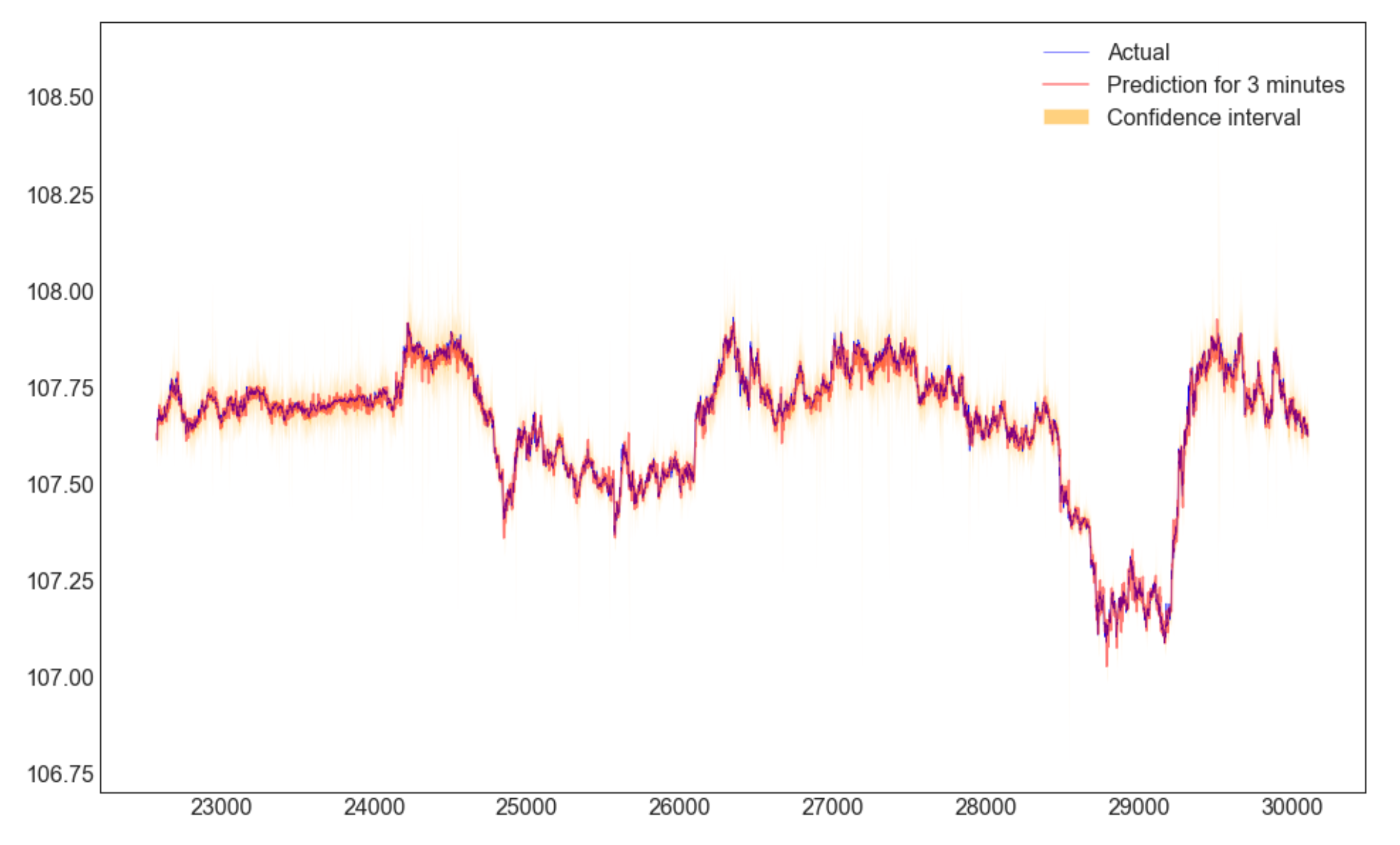
＝＞　92%くらいの予測結果が信頼空間に落ちました

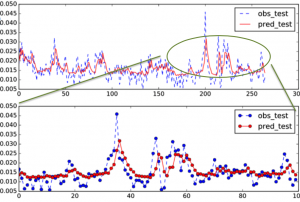
グラフ

• 訓練＋テスト

• テスト詳細

最後に

次世代システム研究室では、グループ全体のインテグレーションを支援してくれるアーキテクトを募集しています。インフラ設計、構築経験者の方、次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。

皆さんのご応募をお待ちしています。