2020.07.07

量子機械学習～量子古典ハイブリッドによる機械学習の実践～

こんにちは、次世代システム研究室のT.I.です。

今回は先日に社内勉強会で発表した量子機械学習に関して、その解説と資料を共有したいと思います。

発表資料に加筆修正したものは以下のpdf fileとなります。

Quantum Machine Learning

目次

      1. 量子コンピュータとは？
      2. 量子機械学習で分類問題を解いてみる
      3. 補足資料：量子とは何か
      4. 補足資料：ゲート式量子計算
      5. 補足資料：量子回路計算の実例

     

    量子コンピュータとは？

    量子コンピュータとは量子のもつ特殊な性質を応用した計算機のことです。従来のコンピュータよりも、一部の問題については飛躍的に高速に問題を解ける可能性が示されており、世界中で研究開発が進められています。特に、昨年ではGoogleがスーパーコンピュータで１万年かかる計算を量子コンピュータでわずか200秒で解決したことは大きな話題となりました。

    量子コンピュータにはアニーリング式とゲート式という２種類があるのですが、Google の開発したのは後者です。ゲート式の量子コンピュータは汎用的な用途に応用できるので期待されている方式なのですが、その開発は技術的に極めて難しい課題です。以下の図は、量子コンピューターの性能の指標である qubit の数をプロットしたものです。現在、50 qubit 程度のマシーンが開発されていますが、例えば暗号解読などの実用的なタスクへ応用するためには少なくとも100万以上の qubit が必要だとされおり、まだまだ人類の技術の及ばぬものであることが判ります。

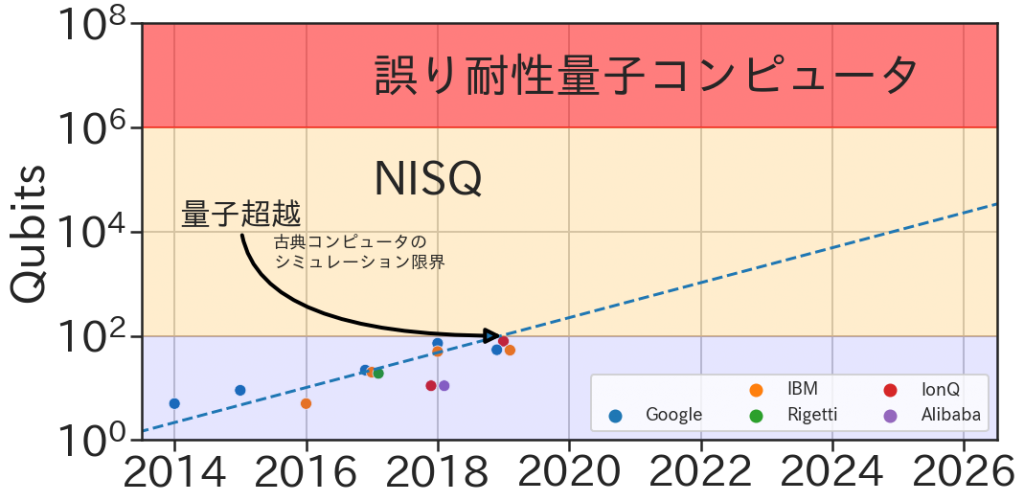
    しかし、Noisy Intermediate Scale Quantum (NISQ) という概念が提唱されています。これは汎用的な量子アルゴリズムには利用できませんが、古典的な計算と組み合わせることで実用的な計算の可能性が期待されるスケールの量子コンピュータです。現在、NISQデバイスを応用するアルゴリズムの研究が進められています。今回紹介する量子機械学習とはその１つで、通常の機械学習モデルの計算の一部に量子回路を組み合わせることで、NISQデバイスを活用しようとするアプローチです。

  2. 今回のブログでは主に量子機械学習の実践についてまとめますが、社内勉強会での資料を基にして、量子コンピュータの基礎についても解説も補足資料として加えてあります。量子や量子コンピュータになじみのない方は先にそちらを参考にしていただければ幸いです。

    量子機械学習で分類問題を解いてみる

    さて、量子回路を用いた機械学習、量子機械学習で実際に問題を解いてみたいと思います。

    量子機械学習と言いましても、以下のような様々なモデルが提唱されています。

    • 量子回路学習(Quantum Circuit Learning) [Ref. arXiv:1803.00745(2018)]
    • 量子畳み込みニューラル・ネットワーク [Ref. Nature Phys. 15, 1273-1278(2019)]
    • 量子敵対的生成ネットワーク [Ref. arXiv:1804.09139(2018)]
    • 量子サポート・ベクター・マシーン [Ref. arXiv:1307.0471(2013), Nature 567, 209-212(2019)]

    他にも強化学習など様々な機械学習モデルへの量子回路の応用が研究されています。

    今回は、量子回路学習を実践してみたいと思います。量子回路学習の概要は以下の図にまとめたとおりです。

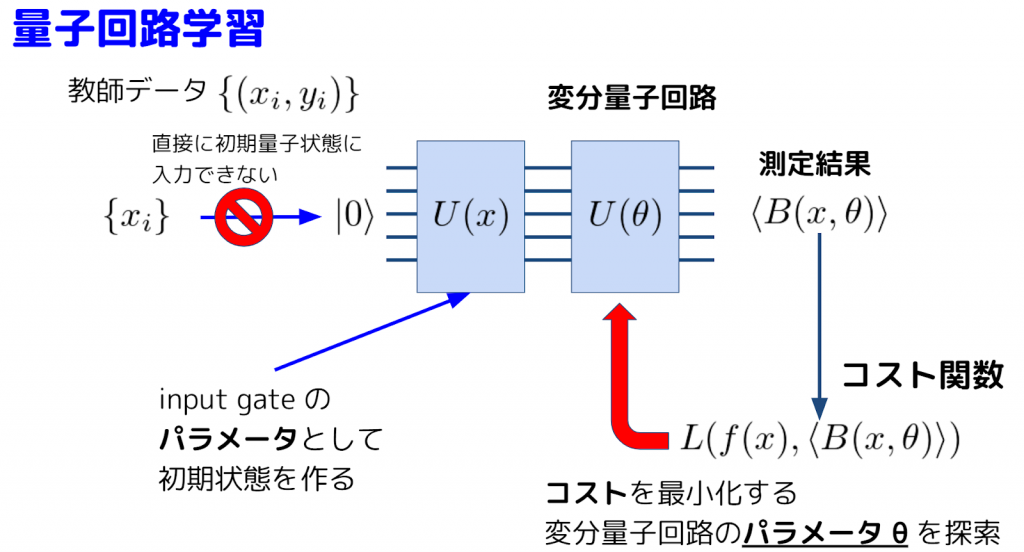
    教師あり機械学習なので教師データを量子回路に入力する必要があります。しかし、現在のNISQデバイスではQuantum Random Access Memory (QRAM)がないため、量子コンピュータに効率的にデータを転送できません。そこで、回路の前半で入力ゲートのパラメータとして与えます。その後、変分量子回路で量子計算を実行した後に状態を測定します。測定結果から計算されるコスト関数を最小化するように変分量子回路のパラメータの更新します。このモデルの利点として、qubit を利用することにより指数関数的に表現力が高まり、更に、量子ゲート演算の制約(unitarity)から機械学習で注意が必要な過学習を避けることができると期待されています。

    では、実際に簡単な量子回路学習を作成して実行してみたいと思います。

    課題は機械学習の(定番)テスト・データとしてアヤメの分類を行ってみたいと思います。入力は花びらの長さと幅、そして出力は３種類の花の種類となります。

    以下は実際に実装した量子回路学習のモデルの概略になります。まず、２つの入力を量子回路に入力します。量子回路では、RY-gateの回転角として入力を受け取ります。２つの qubit は、CNOTによりもつれ合い、更にRY-gateによる回転を２度繰り返し、測定されます。量子回路の出力は、通常のニューラル・ネットワークの層で変換後に、Softmax による活性化で３つのクラスへの分類される確率を出力します。

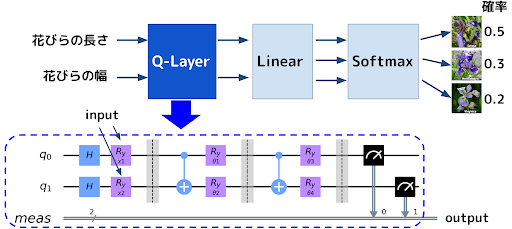
    これらの実装では今回はXANADUの開発している PennyLane という framework を採用しました。PennyLaneはpluginを使って他の様々な量子計算ライブラリや機械学習ライブラリを組み合わせることができます。

    PennyLaneが公開しているTutorialのコードなどを参考に実装したコードは以下の通りになります。順番にJupyter Notebook や Google Colaboratory で実行できます。なお、量子回路の実行は量子コンピュータ実機ではなく、PennyLaneのエミュレータを用いています。

    1. 量子回路の作成

    なお、Google Colaboratory で実行の際にはPennyLaneをinstall後に一度、runtime を restart する必要があるので注意してください。

  3. #!pip install pennylane pennylane-sf
import torch
from torch.autograd import Variable
import pennylane as qml
n_qubits = 3
q_depth = 2
q_delta = 0.01
 
dev = qml.device('default.qubit', wires=n_qubits)
 
@qml.qnode(dev, interface='torch')
def quantum_net(q_input_features, q_weights_flat):
   q_weights = q_weights_flat.reshape(q_depth, n_qubits)
 
# H-layer
   for idx in range(n_qubits):
       qml.Hadamard(wires=idx)
 
# Input Gate
   for idx, q_input_feature in enumerate(q_input_features):
       qml.RY(q_input_feature, wires=idx)
 
# Variational Gate
   for k in range(q_depth):
       for idx in range(0, n_qubits - 1, 2):
           qml.CNOT(wires=[idx, idx+1])
       for idx, q_weight in enumerate(q_weights[k]):
           qml.RY(q_weight, wires=idx)
   exp_vals = [qml.expval(qml.PauliZ(position)) for position in range(n_qubits)]
   return tuple(exp_vals)

    2. 機械学習モデルの作成

  4. これはPyTorchを元にモデルを作成します。モデルの一部として先ほど作成した量子回路を組み込みます。
  5. import torch.nn as nn
 
class QML_Model(nn.Module):
   def __init__(self, input_dim):
       super().__init__()
       self.q_params = nn.Parameter(q_delta * torch.randn(q_depth * n_qubits))
       self.post_net = nn.Linear(n_qubits, 3)
 
 
   def forward(self, input_features):
       q_in = input_features * np.pi / 2.0
       q_out = torch.Tensor(0, n_qubits)
 
       for elem in q_in:
           q_out_elem = quantum_net(elem, self.q_params).float().unsqueeze(0)
           q_out = torch.cat((q_out, q_out_elem))
 
       post_out = self.post_net(q_out)
       x = nn.functional.softmax(post_out, dim=1)
 
       return x

    3. データ準備

  6. scikit-learn を利用してテスト・データを読み込み、前処理をします。
  7. from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
 
features, labels = load_iris(return_X_y=True)
features = features[:,2:] # only sepal length/width
scalar = MinMaxScaler(feature_range=(-1, 1))
features_std = scalar.fit_transform(features)

features_train,features_test, labels_train, labels_test = train_test_split(features_std, labels, random_state=42, shuffle=True)

    4. 学習の実行

  8. PyTorchのoptimizerを用いて学習を進めます。ロスとしてcross entropy loss を最小化するように量子回路のパラメータを最適化します。
  9. import torch.optim as optim
import numpy as np
 
model = QML_Model(features_train.shape[1])
 
optimizer = optim.Adam(model.parameters(), lr=0.05)
loss_fn = nn.CrossEntropyLoss()
 
x_train, y_train = Variable(torch.from_numpy(features_train)).float(), Variable(torch.from_numpy(labels_train)).long()
x_test = Variable(torch.from_numpy(features_test)).float()
iterations = 30
for iteration in range(1, iterations+1):
   y_pred = model(x_train)
   loss = loss_fn(y_pred, y_train)
   print('Iteration {} loss : {:.2f}'.format(iteration, loss.item()))
 
   optimizer.zero_grad()
   loss.backward()
   optimizer.step()

    5. 結果の可視化

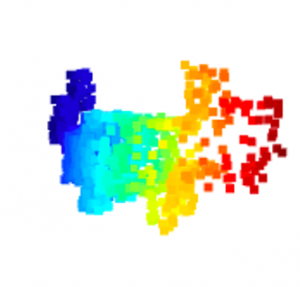
    import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('ticks', {'axes.grid': True})
sns.set_context('poster', font_scale=2.0)
%config InlineBackend.figure_format = 'retina'
plt.rcParams['figure.figsize'] = (12.8, 9.6)
plt.rcParams['figure.facecolor'] = 'white'
 
# 日本語フォントを利用
import japanize_matplotlib # !pip install japanize-matplotlib
 
xls = np.linspace(-1, 1)
xs = np.array(np.meshgrid(xls, xls)).reshape(2,-1).T
x_valid = Variable(torch.from_numpy(np.array(xs))).float()
y_pred = model(x_valid).detach().numpy()
y_pred_label = np.argmax(y_pred, axis=1)
 
fig, ax = plt.subplots(figsize=(12, 12))
for ith in [0, 1, 2]:
   mask = y_pred_label == ith
   ax.plot(xs[mask,0], xs[mask,1], 's', ms=12, alpha=0.2)
 
for ith, m, ll in zip([0, 1, 2], ['o', 'X', 's'], ['Setosa', 'Versicolor', 'Virginica']):
   mask = labels == ith
   ax.plot(features_std[mask,0], features_std[mask,1],
           m, ms=15, color=f'C{ith}', mew=2.0, mec='black', label=ll)
ax.legend(fontsize=32, loc='upper left')
ax.set(xticklabels=[], yticklabels=[], xlabel='花びらの長さ',
         ylabel='花びらの幅', title=f'学習後')

     

     

    さて、これらの量子機械学習の実行結果が以下になります。最初は３種類のクラスへの分類がうまくできませんが、繰り返すうちに学習が進む様子が判ります。

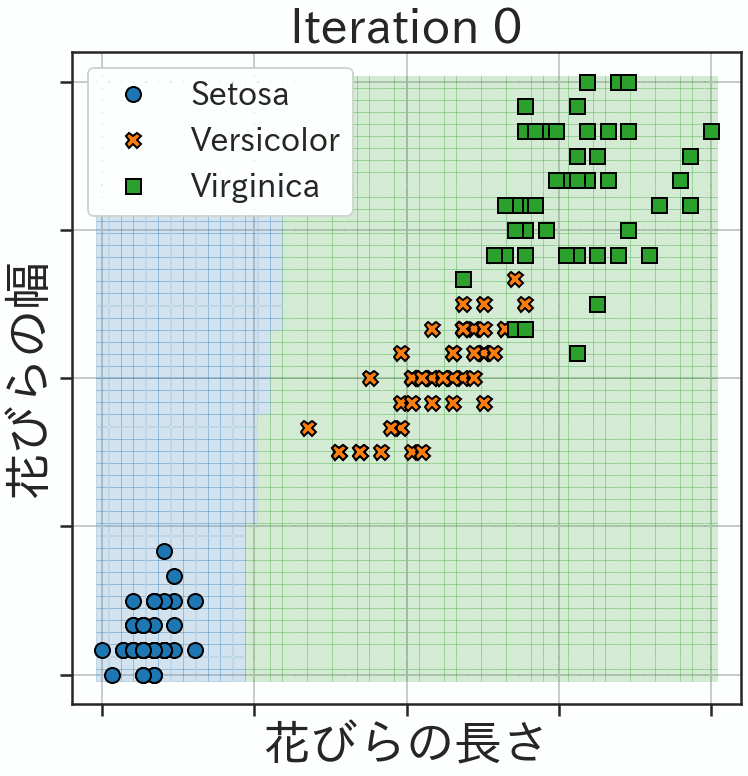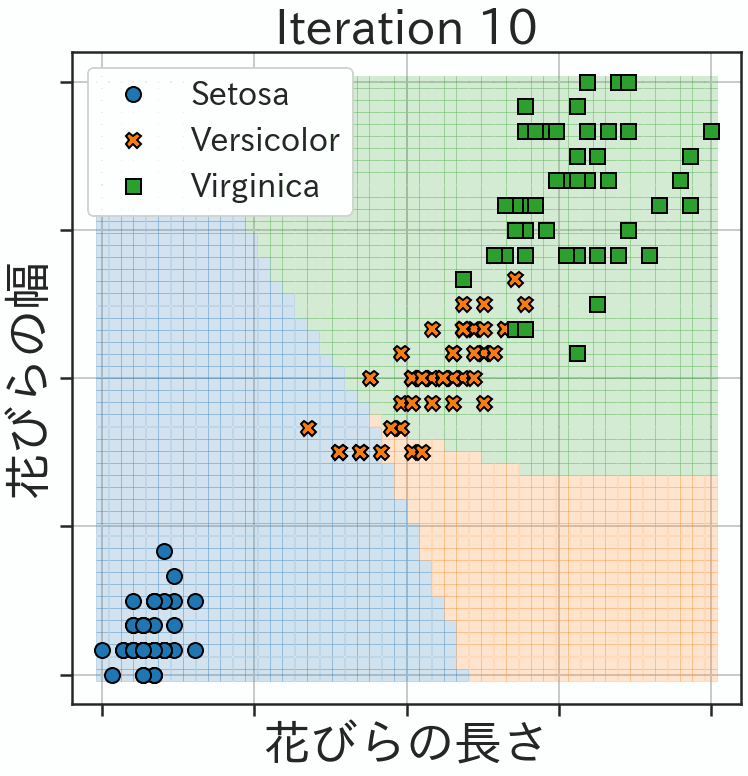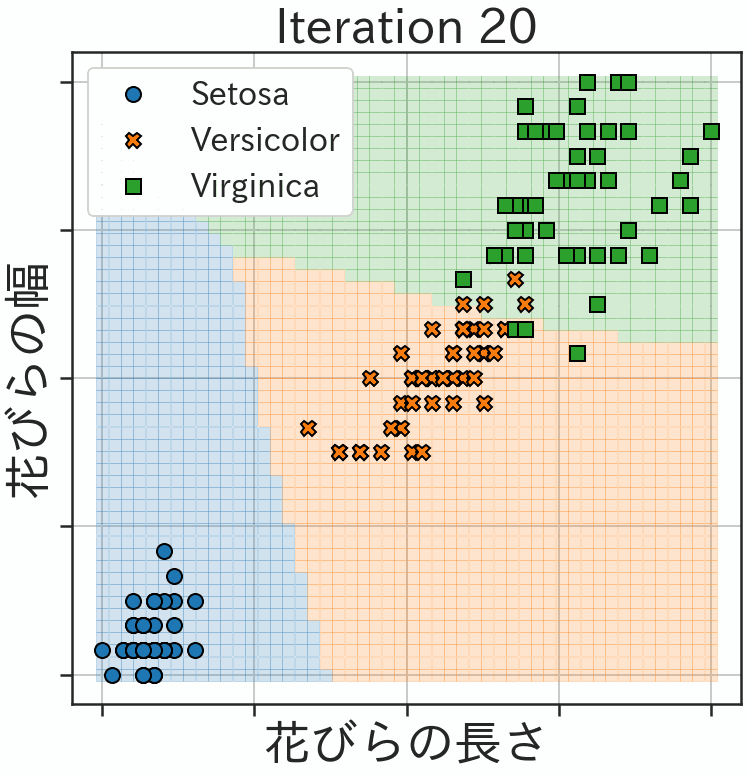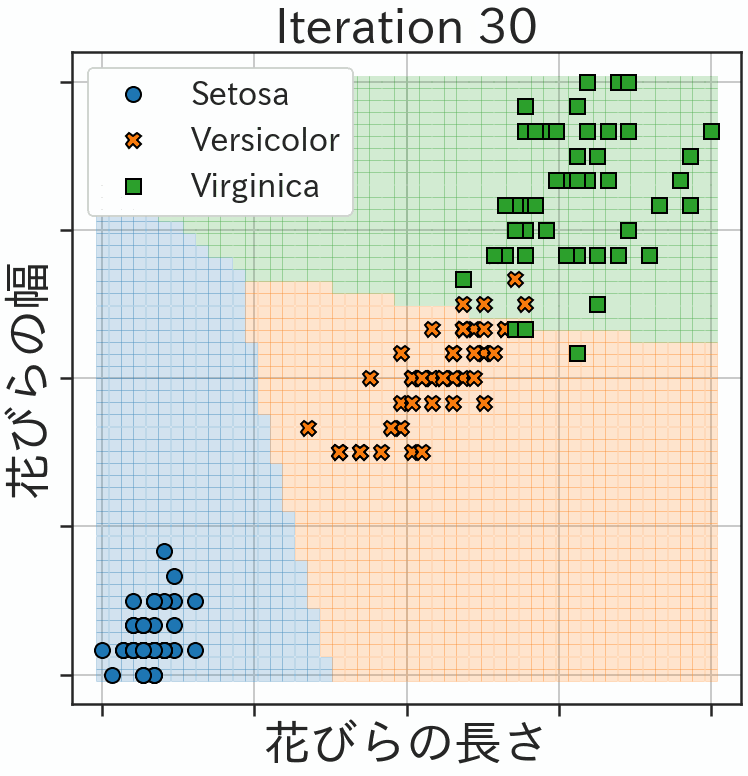
    そして、最終的な学習結果が以下の図になります。３種類のアヤメを量子回路で分類することに成功しました。

     

     

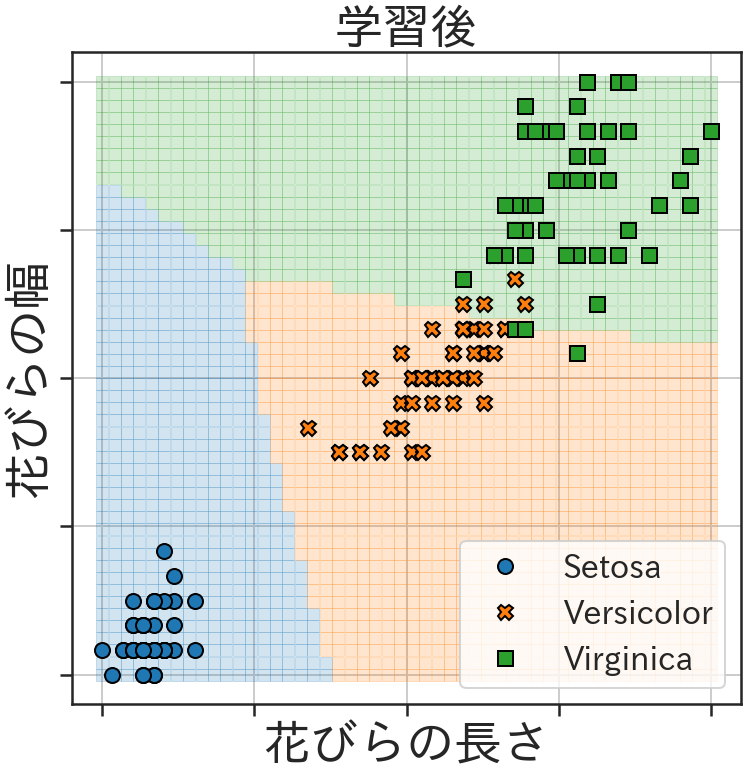
    まとめ

    今回は量子コンピュータの実用的な応用として期待が高まっているNISQデバイスを利用する量子機械学習について、量子コンピュータの基本的な事柄から解説しました。
    量子機械学習はまだ研究が始まったばかりで、従来の古典コンピュータを用いた機械学習に対する優位性なども、これからの検証が必要です。しかし、量子コンピュータの開発は着実に進歩していますし、これからの発展が期待される技術だと思います。

 

  1. 最後に

    次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

     

    参考資料

    Tutorials & Documents

    ・Quantum Native Dojo (日本語) https://dojo.qulacs.org/ja/latest/index.html

    ・IBM Quantum Experience https://quantum-computing.ibm.com/

    ・XANADU PennyLane https://pennylane.ai/

    解説

    ・日本経済新聞「分かる教えたくなる量子コンピュータhttps://vdata.nikkei.com/newsgraphics/quantum-computer-basic/

    ・藤井啓祐「驚異の量子コンピュータ」

     

    更に詳しく勉強したいなら

    ・森川智之「量子計算理論」

    ・佐川弘幸・吉田宣章「量子情報理論」

    ・富田章久「量子情報工学」

    ・西村秀稔・大関真之「量子アニーリングの基礎」

 

補足資料：量子とは何か

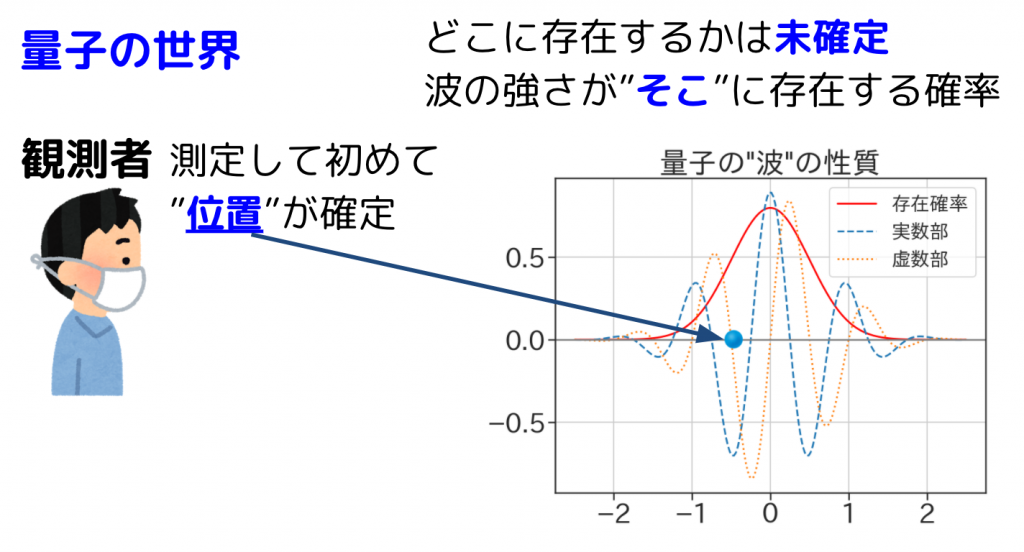
量子とは「粒子」と「波」の２つの性質を同時に持つとても小さなモノの単位です。量子という物質が存在するのではなく、物質を作っている原子や電子、光の粒である光子、など様々なものが量子の性質を持っています。通常、我々の日常ではモノは決まった場所に常に存在しています。一方、量子というのは複素数の波(波動関数)で表現されており、具体的に特定の地点には存在していません。誰か観測者が量子の位置を測定して初めて粒子として存在する場所が決定します。

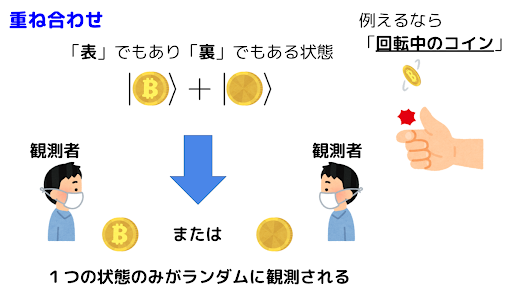
量子重ね合わせ

量子の不思議な性質の一つが複数の状態を同時に取れることです。これは先程の解説で述べた存在する場所が定まらないという意味です。例えますと、回転中のコインのように「表」と「裏」のどちらか定まらない状態になっています。そして、観測者はコインを止めるわけですが、その瞬間に表と裏の重ね合わせが解け、ランダムに表か裏のどちらかが観測されます。

量子エンタングルメント

エンタングルメントはもつれ合いという意味で、これは量子のもっとも奇妙な性質といえます。これは２つ以上の量子の状態が互いに関係したうえで重ね合っている状態です。ここで簡単な例として２枚のコインを考えます。

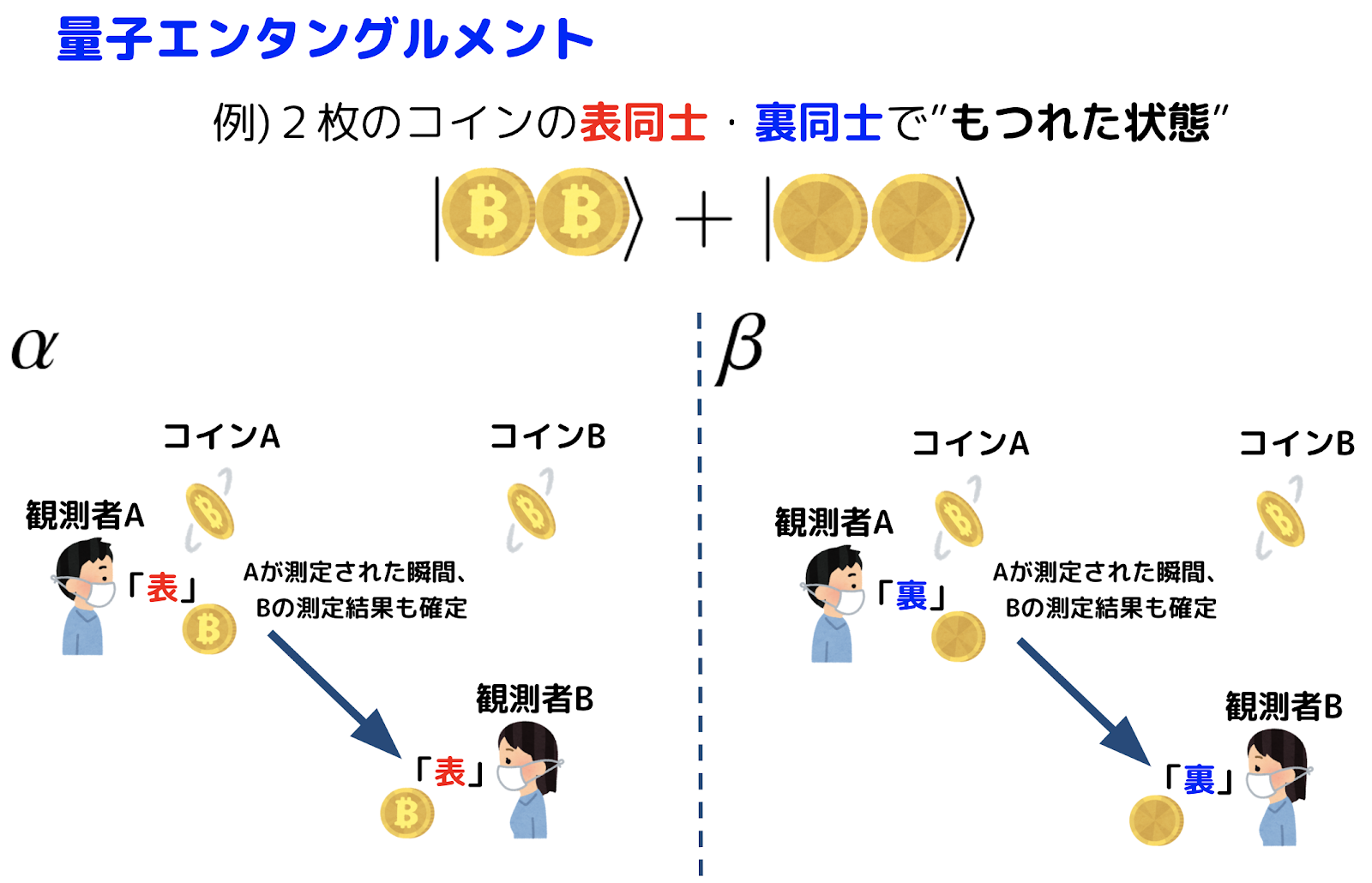
観測者Aが一方のコインを観測します。観測するまでコインAの状態は未確定ですが、αの場合では、「表」を観測しました。エンタングルしていると、この瞬間にコインBの測定結果も「表」で確定します。βの場合では「裏」を観測した結果、コインBも「裏」で測定結果が確定します。

エンタングルメントの不思議な点は、コインBを観測していないにも関わらず、コインAを観測したことで、Bの測定結果がまでが決まってしまうことです。時として、これをテレパシーのようにコインAの情報がコインBに伝わったと誤って解釈されてしまうことがあります。しかし、意味のある情報がコインAからコインBに伝達されていませんし、観測者間の通信には利用できないので注意してください。

量子ビット(qubit)

上記で解説した「重ね合わせ」と「エンタングルメント」の性質を持つ量子ビットを用いてゲート式量子コンピュータは計算します。通常の古典ビットが０か１の一方の値しか取りませんが、qubit は０と１との重ね合わせ状態で、以下のように表されます。

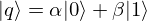
\begin{align*} |q\rangle = \alpha | 0 \rangle + \beta | 1 \rangle \end{align*}

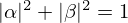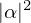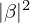ここで、αとβは\begin{align*} |\alpha|^2 + |\beta|^2 = 1 \end{align*}を満たす複素数で、先ほどのコインの例のように０または１が測定される確率は、それぞれ、\begin{align*} |\alpha|^2 \end{align*}と\begin{align*} |\beta|^2 \end{align*}となります。量子コンピュータが高速な理由は、この qubit の重ね合わせにより指数関数的に大量の状態を一度に計算できる点にあります。

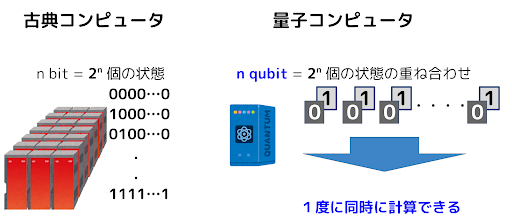
ただし、量子コンピュータが一度に計算できるとしても、それは求めている答えも含めた膨大な状態の重ね合わせなので、正解を抽出するアルゴリズムが必要です。その探索が指数関数的に増えるのであれば、量子コンピュータの優位性はなくなるので注意が必要です。

 

補足資料：ゲート式量子計算

量子の性質と qubit について簡単に解説しましたが、具体的にゲート式量子コンピュータではどのようなことをしているかについて、解説したいと思います。

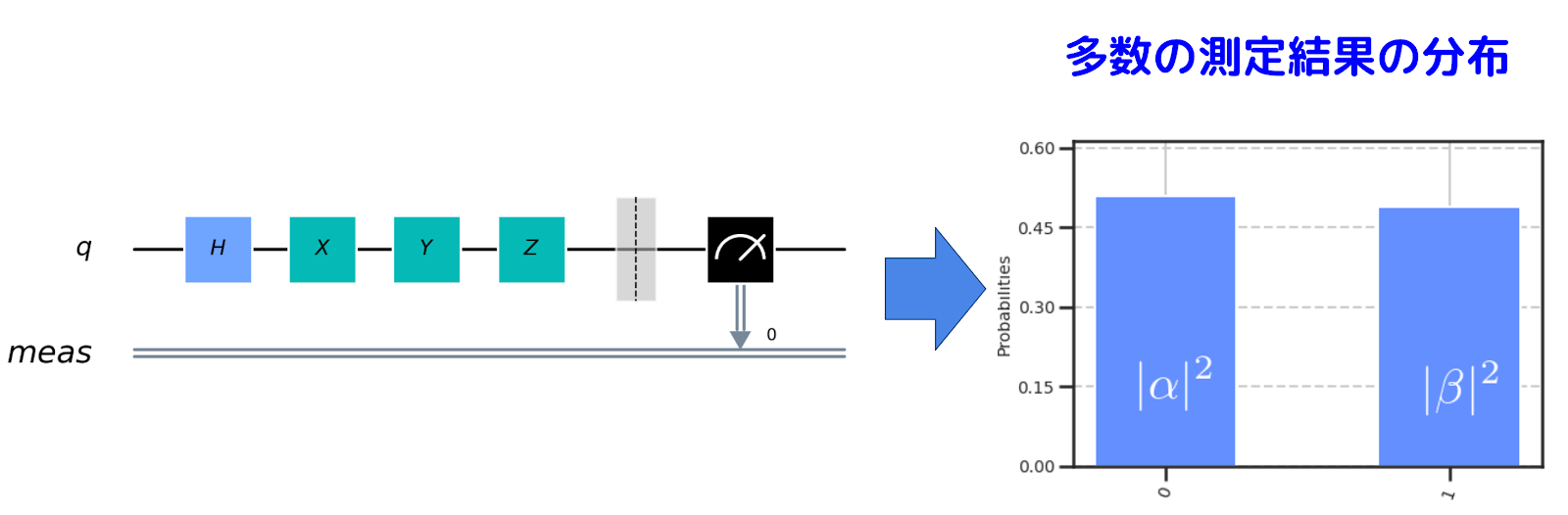
上図はゲート計算の例となります。入力されたqubit に対して、様々な種類のゲートで操作し、最後にqubitを測定し、古典的なビットとして集計します。一度の測定では０か１の一方しか観測されませんが、多数の測定を行うことで qubit の状態を推定できます。

特にqubitは以下のように球面(Bloch sphere) の１点として表現することもできます。そして、量子ゲートはこのベクトルの向きを様々に回転させる操作として表されます。

量子ゲートの例

アダマール・ゲート

アダマール・ゲートでは量子重ね合わせ状態を作る際に用いられます。具体的には以下のような qubit の操作となります。

\begin{align*} H|0\rangle &= \frac{1}{\sqrt{2}} \left( | 0 \rangle + | 1 \rangle \right) \\ H|1\rangle &= \frac{1}{\sqrt{2}} \left( | 0 \rangle - | 1 \rangle \right) \\ \end{align*}

制御NOT(CNOT)

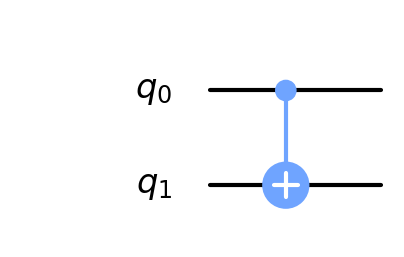
制御NOTでは、control bit (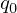\begin{align*} q_0 \end{align*}) と target bit (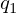\begin{align*} q_1 \end{align*}) の２つの qubit を入力に受け付けます。control bit が１のときに、target bit を反転させる操作に対応し、エンタングル状態を作る際に用いられます。

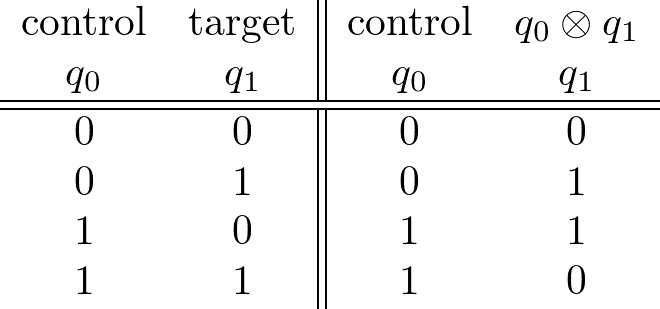
補足資料：量子回路計算の実例

具体的に量子回路を用いた簡単な計算を実行してみたいと思います。ここではQiskitというpythonのlibraryを利用します。

1. 量子回路の作成

Qiskit により量子回路を作成するコードは以下のようになります。

#!pip install qiskit
from qiskit import QuantumCircuit

qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
qc.measure_all() # 測定
qc.draw('mpl')

ここでは２つのqubitの回路を作成し、一方にアダマール・ゲートを作用させたのちに、CNOTを加えました。これにより状態は

\begin{align*} |0 \rangle \otimes | 0 \rangle &\xrightarrow{H} \frac{1}{\sqrt{2}} \left( | 0 \rangle + | 1 \rangle \right) \otimes | 0 \rangle \xrightarrow{\mathrm{CNOT}} \frac{1}{\sqrt{2}} \left( |00\rangle + |11\rangle\right) \end{align*}

とエンタングルしたペアとなります。最後に両方の qubit を測定します。このコードを実行すると以下のような回路図が出力されます。

 

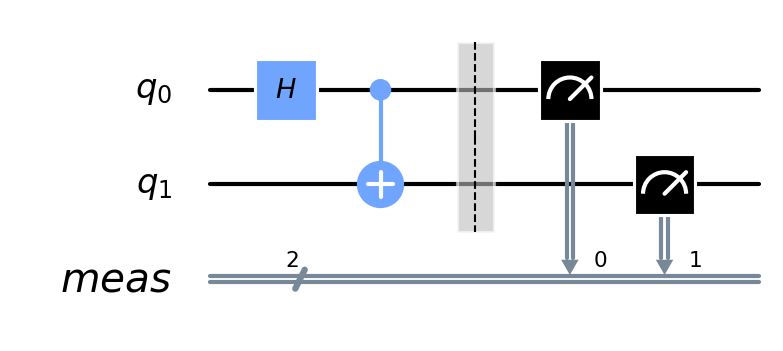
2. 量子状態の測定

この回路を実行してみます。まずは、Qiskit の量子計算をシミュレートするモジュールを用いて実行します。

from qiskit import BasicAer, execute
from qiskit.visualization import plot_histogram

backend = BasicAer.get_backend('qasm_simulator')
result = execute(qc, backend=backend).result()
counts = result.get_counts()
plot_histogram(counts)

実行結果は以下の通り、期待されているように２つのqubitは必ず同じ00または11のペアとして観測されました。

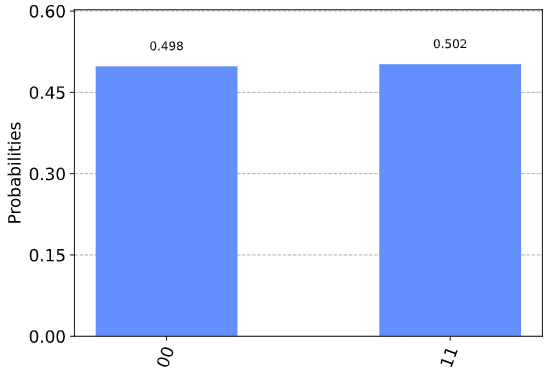
3. 実際の量子コンピュータでの実行

IBM Quantum Experience のアカウントを作成すると、トークンを取得して認証するだけで上記の量子回路のシミュレーションを”本物”の量子コンピュータで実行できます。

以下のそのためのコードです。

from qiskit import IBMQ
from qiskit.prividers.ibmq import least_busy

# アカウントを認証してbackendを修正するだけ
IBMQ.save_account(my_token)
provider = IBMQ.load_account()
backend = least_busy(provider.backends(
        filters=lambda b: b.configuration().n_qubits >= 3
        and not b.configuration().simulator
        and b.status().operational==True))

# 実際の量子コンピュータで実行
job_exp = execute(qc, backend=backend, shots=8192)
exp_result = job_exp.result()
exp_measurement_result = exp_result.get_counts(qc)
# 結果のプロット
plot_histogram(exp_measurement_result)

さて、結果ですが、実機、IBM Q (NISQデバイス) で実行した場合、ノイズのために01, 10 の状態も僅かにですが観測されていることが判ります。

  • Twitter
  • Facebook
  • はてなブックマークに追加

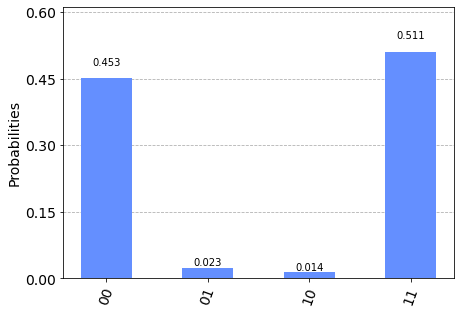
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。

 
  • AI研究開発室
  • 大阪研究開発グループ

関連記事