UC Berkeleyの深層強化学習コース（CS294）：Advanced Q-learning
次世代システム研究室のL.G.Wです。今回は、前回の続きで、UC Berkeleyの深層強化学習コースを解説します。前回もQ-learningを触れましたが、ここは、高度なQ-learning方法をより詳しく解明します。
アウトライン
- 一般Q-learningの欠点及び改善対策
- Q-learning方法の汎用フレームワーク
- 連続動作空間におけるQ-learning
- Q-learning精度チューニングのTips
一般Q-learningの欠点及び改善対策
サンプル間の相関が強い
一般のOnline Q-learningは、下図に示したようなロープで学習する。まずは、動作を執行し、報酬と次の状態を得られ、これを次ステップの学習サンプルになる。ところで、これらの学習サンプルが連続で獲得するせいで、独立性を失ってしまう（つまり、i.i.dではない）。例えば、自動運転の場合、状態は道路（軌跡）とすると（下図の下部を参照）、次の状態は前の状態に緊密に依存し、学習のTarget数値も連続変化することで、ローカル予測に落ちで、Globalな最適数値に永久に到達できなくなる。
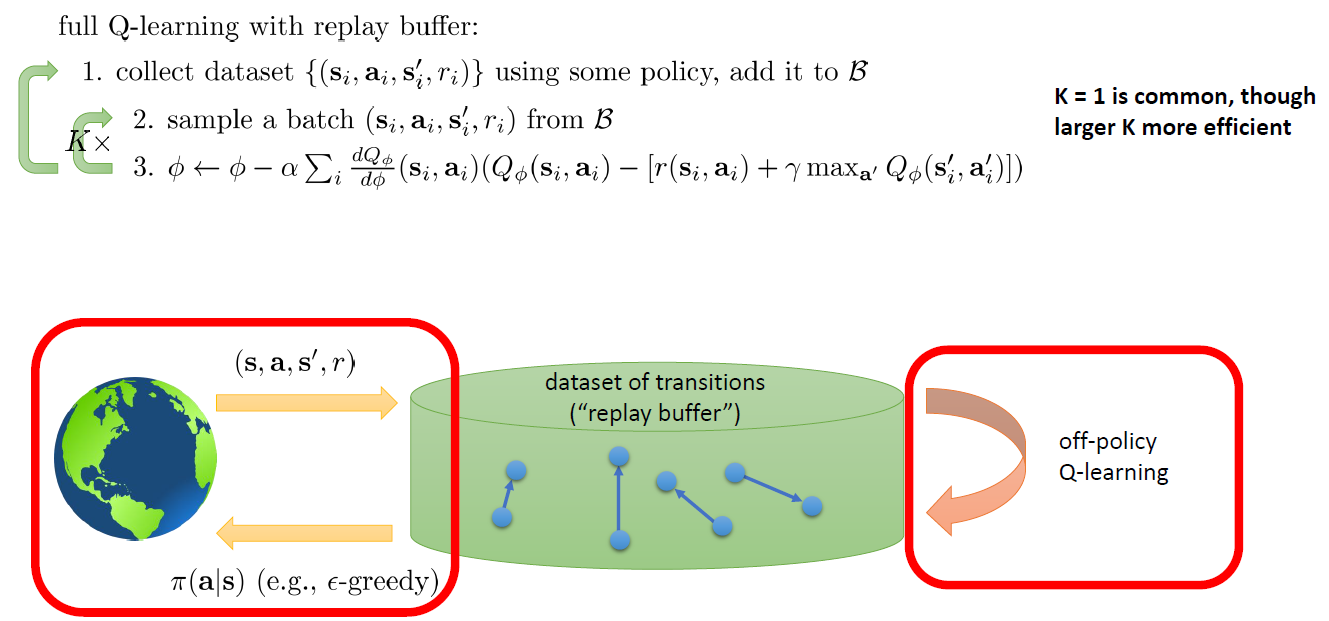
この欠点に対する対策は、二つがある。（１）並列学習：サンプルの時系列相関を壊し、並列度に合わせて連続サンプルを分けて同時学習する。（２）Replay Buffer: 下図のように、(s_i, a_i, s_i+1, r_i)をReplay Bufferに追加して、パラメータΦを学習ために、そのReplay Bufferからランダム的にK個のサンプルを取り出す。そのサンプルらはランダムなので、時系列の相関がなくなる。さらに、MiniBatch（Size=K）でGradientを計算するので、Gradientの分散も下げ、学習の安定性が増える。
収束しにくい
下図のように、もう一つ欠点は、パラメータΦを更新するのに、Gradientはこのターゲットの微分ではない。そうすると、Convex関数でも必ず収束することはありません。Gradientを計算する度にターゲットValue（φ）が変わるので、収束スピードがノイズに大きく影響される。
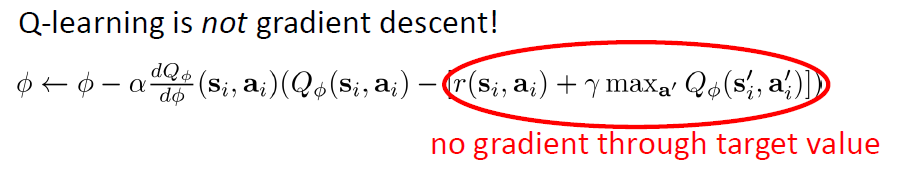
対策としては、下図のように、Reward計算用のQ関数φ’と現在のAction選択用のQ関数φをそれぞれ別のネットワークで表現する。そうすると、Gradient計算式の内部には、ずっと同じφ’を使い、そのφ’の更新は、N*K回後で行うことで、収束の安定性が劇的に向上される。さらに、φ’の更新は、N*K回で急に変わることも不自然なので、Polyak averageを利用して、毎回少しずつ更新していくこともよい。
Q-learning方法の汎用フレームワーク
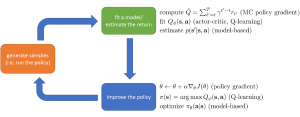
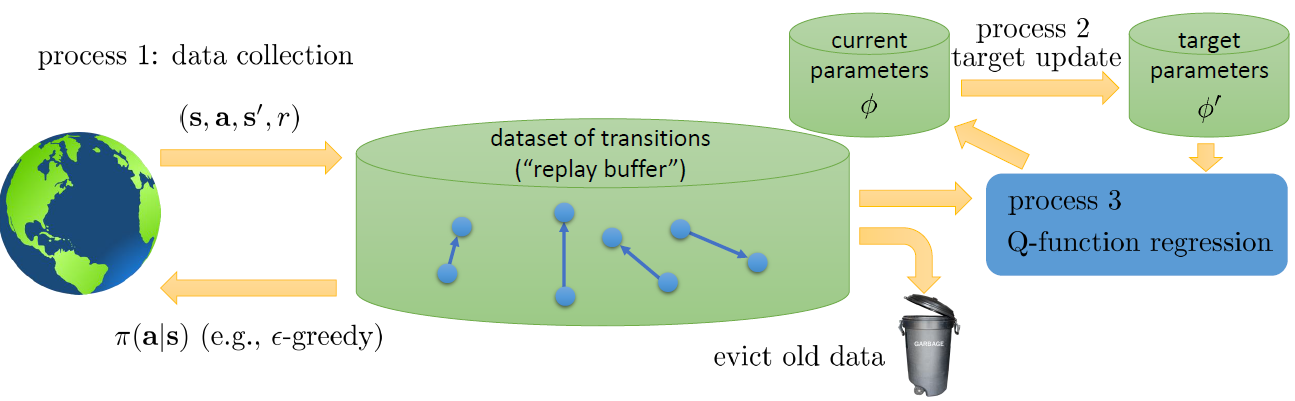
Q-learningの三つ方法を纏めると、下図のような統一フレームワークになる：（１）Online Q-learning: On policyの学習で、Process 1、Process 2とProcess 3は同じスピード（Iteration）で実行される。学習の効率が悪いし、収束も保証されない。（２）DQN： Process 1とProcess 3は同じスピードで実行され、Process 2（つまり、ターゲットNetworkのパラメータの更新）は緩める。Target NetworkとAction Networkが分けられることで、学習精度とスピードが良くなる。（３）Fitted Q-iteration: Process 1のローブ内に、Process 2が実行され、プロセス２のロープ内にプロセス3が実行されるような、Cascade型の学習である。性能の面では、DQNとほぼ同じ水準になる。
連続動作空間におけるQ-learning
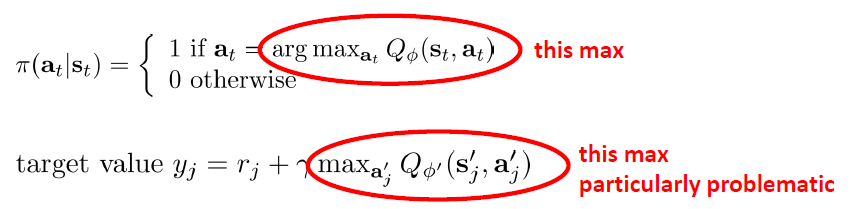
もし動作空間が連続である場合、上記のようにすべてのアクションにMaxのQ値を計算するのは、とても無理だある。要するに、Q関数は、複雑なネットワークで、Max値は解析解ではなく、すべてのActionを反復計算するしかない。この場合におけては、下記の三つSolutionが考えられる。
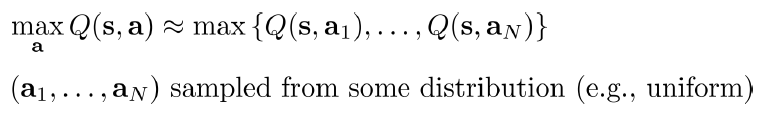
（１）単純にサンプリング：上記のように、ある分布から（例えば、Uniform分布）N個のActionをサンプリングし、そのN個ActionのQ値を計算してから、最大値を取る。正確ではないものの、極めてシンプルし、分散計算も可能であるから、よく使われる。もっと精度をあげるなら、Cross Entropy Methodで最適化することもある。
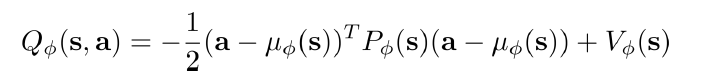
（２）解析できるQ関数を作る：Q関数を上記のように定義する。Q関数は、Actionの2次関数なので、最大値Maxは解析解がある。つまり、最大値を取るのは、Action＝μ（ｓ）になる。このSolutionは、Q関数の定義を変更するだけで、アルゴリズムには何も変更しない。ただし、Q関数は、Actionの2次関数で固定されるので、複雑なQ値分布を表現できなくなる。
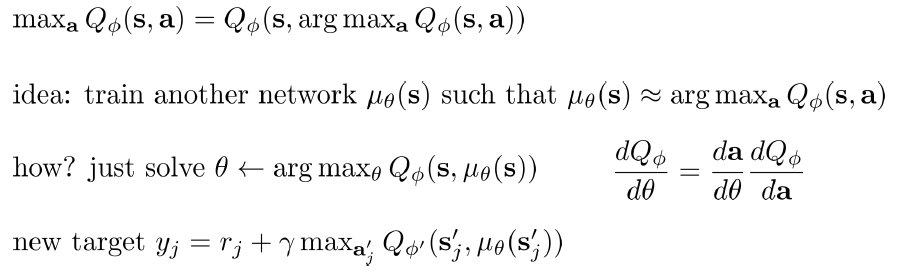
（３）Q関数のMax関数を学習する：Q関数のArg Maxを別ネットワーク（θ）で表現する。そのネットワーク（θ）の微分は、Q関数のネットワーク（Φ）対Actionの微分にAction対θの微分を掛けることになる。下図のように、ΦとθのTarget NetworkとCurrent Network, 合わせて4つネットワークを同時に学習する。それは、DDPG (Deep Deterministic Policy Gradient)という手法である。
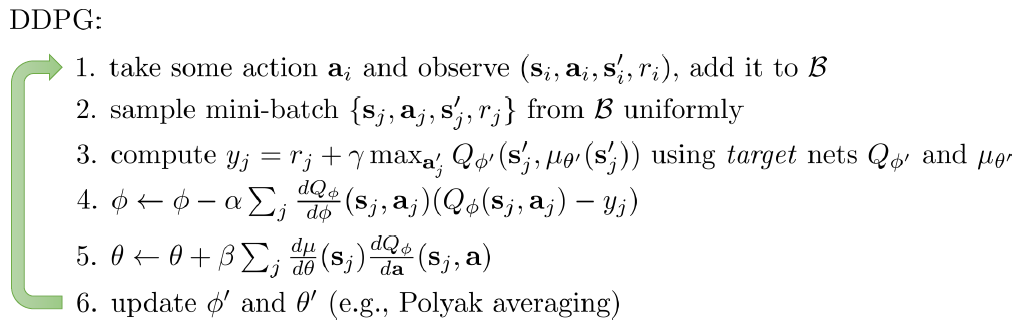
Q-learning精度チューニングのTips
（１）Q値の過大評価
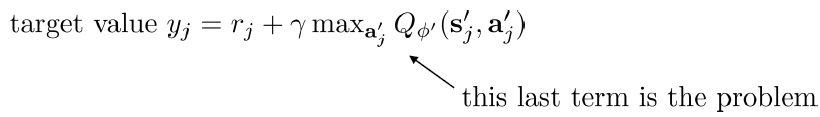
上記のTarget Valueに、最大のQ値は過大評価の恐れがある。なぜならば、下記のように、Q関数は正確ではなくて、ノイズがあるから、Maxを取ると、極めて高い確率でノイズのQ値を取る。Actionを選択する時は、最大のQ値に対応するActionを選ぶ。もし異常に高いQ値（ノイズ）があれば、必ずそれに相当するActionを決める。そして、Q値を計算する時も、また同じQ関数を使うので、そのActionのQ値は必ずノイズのQ値になる。
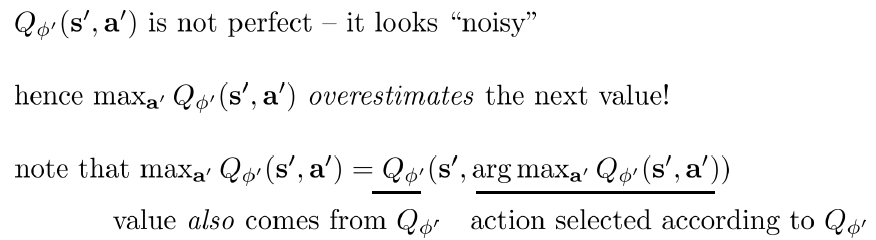
解決策としては、下図のように、Actionを決めるQ関数とQ値を計算するQ関数は別々のネットワークを作る。そうすると、もしこの二つネットワークがそれぞれ違いタイミングでノイズが入れば、必ずしも異常なAction（ノイズ）を選ぶことはない。その二つネットワークは、前述のQ-learningに定義したTarget NetworkとCurrent Networkを再利用すればよい。これはDouble Q-learningと呼ぶ。
（２）実用なTips
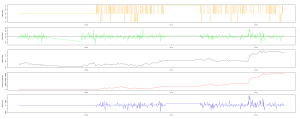
- Q-learningの安定性： Q-learningは、簡単なタスクなら、収束性が問題ないが、複雑なタスクの場合、毎回実行しても成績が変わるし、時々は全く学習できていないこともある。
- Replay Buffer: 容量が大きいReplay Bufferは、学習の安定性を改善する。Fitted Q-iterationも同じ効果がある
- 学習時間： Q-learningの学習時間が極めて長いので、最初は全くランダム的な動きでも、Iterationを増やせば、改善していくはず
- Exploration: 学習の最初段階は、大きい割合で探索する、つまり最大Q値のActionを選ぶ確率を下げる。そのうち、徐々に上げていく
- Gradientが時々非常に大きくなり、学習効率がゼロになるおそれがある（Gradient Explosion）。Gradientをある閾値までClipするのは、有効な対策である
- Double Q-learningは、基本的に性能を改善する。そして、副作用もないので、必ず利用すべき
- 段階分けのExploration率（ε）、高いから低いまで変化していくの学習率（learning rate）が有効なTipsである。Adam Optimizerが進められる。
- 毎回実行は、同じ成績が出るとは限らないので、複数Random Seedを設定し、複数回を実行して成績を確認すべき
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
皆さんのご応募をお待ちしています。
