Neural Processの紹介
[mathjax]
イントロダクション
こんにちは、次世代システム研究室のK.N.です。今回は2018年にDeepMindから発表されたNeural Process(NP)の論文について読んだのでご紹介したいと思います。同著者から同時期に２報[1,2]発表されておりますが、本質的には変わりません。[1]のほうは[2]の一般形になっており、本ブログではの内容について説明いたします。しかし、[2]のほうが背景や数値検証等の説明がより丁寧だと思いましたので、両方読むことをオススメします。今回は、[1,2]を参考に実装及び簡単な数値検証を行いました。まず、NPを一言で表すと、NN(Neural Network)関数を確率過程に適用したモデルということになります。確率過程は、為替や株価といった時間経過といったランダムな動きを示す変数を表すモデルとして金融工学でよく用いられる印象ですが、機械学習分野では、専らGaussianProcess(GP)がその代表例として登場します。GPは、カーネルを利用したノンパラメトリックな回帰モデルになります。論文内でも、NPはGPの考え方を引き継ぎつつ、そのデメリットを克服するのとして登場しますので、まずGPについて簡単におさらいしたいと思います。
GP(Gussian Process)
手法
確率過程では、関数空間（関数を成すベクトル空間）上で値を持つ確率変数が従う確率分布を考えます。GPは確率過程の一つです。簡単に出力が１次元の実数関数\(f: X \rightarrow Y\)を考えたとき、\(f\)がガウス過程に従うとは、任意の有限個の\(X\)の元に対する関数が取る値\((f({x}_{1}), f(x_{2}), f(x_{3}), \ldots )\)の同時分布が正規分布に従うことを言います。この定義に素直に従うと,入出力の組\(\{ ({\bf x}_{i}, y_{i}) \}_{i=1}^{n}\)に対して,\(y_{1:n}\)の確率分布が
$$
p(y_{1:n}|{\bf x}_{1:n}) = N({\bf \mu} ({\bf x}_{1:n}), {\bf \Sigma} ({\bf x}_{1:n}) )
$$と書けることを意味します。\(\ ({\bf x}_{1:n},y_{1:n})\)はそれぞれ\(({\bf x}^{T}_{i}, y_{i})\)を\(i=1\)から\(n\)個まで縦に並べたものです。\({\bf \mu}({\bf x}_{1:n})\)と\({\bf \Sigma}({\bf x}_{1:n})\)はそれぞれ、\(y_{1:n}\)の平均値ベクトルと共分散行列を返す関数になります。もちろん、共分散行列は半正定値である必要があります。ここで、\({\bf y}\)の平均に関する事前情報を推定する方法は無いのでゼロベクトルとしてもよいでしょう。共分散行列は異なる\({\bf x}\)と\({\bf x}’\)が互いに近い距離に位置するならば、\(y\)と\(y’\)も似たような値を持つと考えるのが自然です。そこで,\({\bf x}\)の２点間の距離を測るカーネル関数\(k({\bf x},{\bf x}’)\) を共分散行列の要素に用いることとします。やや強引ですが、\({\bf y}\)の分布は
$$ p(y_{1:n}|{\bf x}_{1:n}) = N({\bf 0}, {\bf K})
$$と表されることになります。ただし、\(K_{i,j}=k({\bf x}_{i},{\bf x}_{j})\)です。カーネル関数には、色々な関数形が利用可能ですが、代表的なのはガウシアン型\(\exp \left( -|{\bf x}-{\bf x}’|^{2}/l \right)\)や指数型\(\exp \left( -|{\bf x}-{\bf x}’|/l \right)\)が代表的です。また、カーネル関数を組み合わせて新たなカーネル関数を設計することも可能です。
ここで、回帰の問題として、\(C = \{ ({\bf x}_{i}, y_{i}) \}_{i=1}^{m}\)が観測値として与えられたとき、新たに入力\({\bf x}_{m+1:n}=\{ {\bf x}_{i} \}_{i=m+1}^{n}\)から\(y_{m+1:n}\)を予測をするという問題を考えます。ここで、添字ラベルを\(obs=1:m, new=m+1:n\)とします。予測分布\(p(y_{new}|C, {\bf x}_{new})\)はベイズの定理から
$$ p(y_{new}|C, {\bf x}_{new}) = \frac{p((y_{obs},y_{new} )|({\bf x}_{obs}, {\bf x}_{new}))} {p(y_{obs}|{\bf x}_{old})} \\ = N(\mu_{new|obs}, \Sigma_{new|obs})
$$で書けます。ただし、
$$ \mu_{new|obs} ={\bf K}_{new,obs}{\bf K}_{obs,obs}^{-1} y_{obs} \\ \Sigma_{new|obs} = {\bf K}_{new,new}+{\bf K}_{new,obs}{\bf K}_{obs,obs}^{-1} {\bf K}_{obs,new}
$$です。多変量ガウス分布の条件付き分布の公式とその導出は教科書をご参照ください。例えば、PRMLの2.3.1です。
デモ
以上より、GPによる回帰の公式を得ることができました。そこで、簡単な数値検証をしてみたいと思います。ある目標となる関数に対して、与えられた幾つかの観測データを元に、元の関数を予測できるのか検証します。今回の例では、目標関数を\(y = sin(x)\)として、\(x \in [-4,4]\)の範囲内の一様乱数でサンプルした数点を観測データとして使用します。
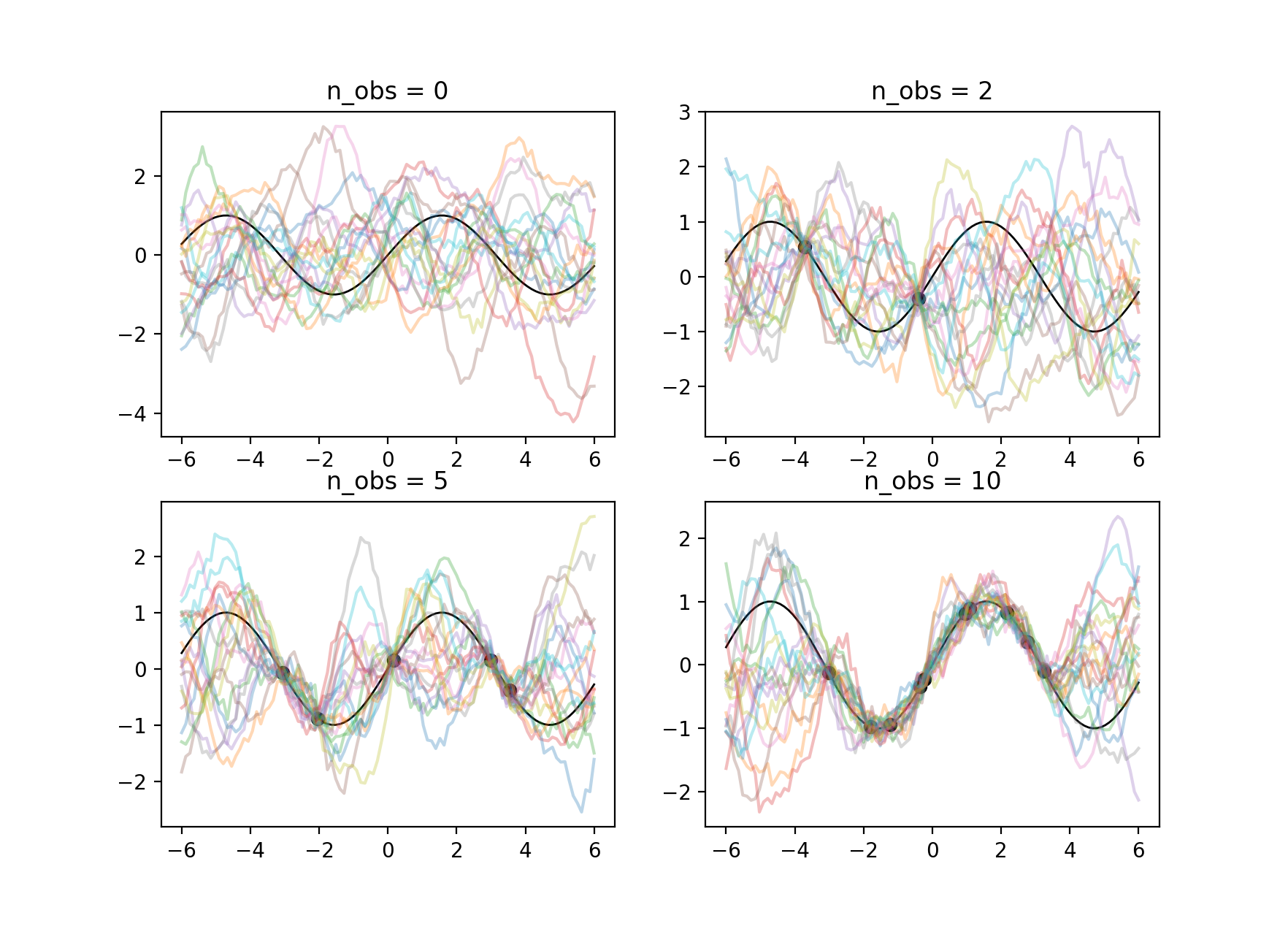
Fig.1: GPによる回帰の結果。観測点の数ごとに並べた。
Fig.1.は観測点（黒点）が0, 2, 5, 10点あった場合のGPによる予測関数のサンプルの結果を示しています。予測関数は色線で、目標関数は黒線です。カーネルはガウスカーネル(\(l=1)\)を用いています。観測点が無い場合、予測関数は事前分布に従い、ただい平均がゼロ付近となっている様子がわかります。予測関数は観測点から離れた領域ではばらつきが大きくなり、点が増えていくにつれて、ばらつきが小さくなり、真の関数に近づいている様子が分かります。十分な観測点があれば予測精度も良く、モデルの学習も必要ないという利点がありますが、GPには以下の欠点があることが知られています。
- データ量に対するスケーラビリティが悪い(\(O(n^3)\))
- 学習データを保持する必要がある。
- カーネル関数では表現できる関数に制限がある。
NP(Neural Process)
手法
NPもGPと解くべきタスクは同じで、観測データで条件付けられる新規入力に対する出力値の予測です。つまり、\(p(y_{new}|C, x_{new})\)をNN関数でモデル化します。これは、観測データにより条件付けられる関数の分布\(f \sim p(f|C)\)を予測することと同値です。GPでは事前分布はカーネル関数により決まり、観測対象となるデータに依りません。GPの事前分布は表現力が高く、どんなデータに対してもそれなりに当てはまりは良いですが、先程のデモで確認したとおり十分な数の観測点がないと関数形が定まりません。逆にNPでは、観測データの入出力を関係付ける\(f\)が\(p(f)\)に従うとすると、\(p\)に一致するようなパラメトリックな分布\(q(f)\)を学習します。その結果、少ない観測データに対しても精度の良い予測が可能になります。このような応用をfew-shot learningなどと呼びます。
NPのグラフィカルモデルと計算ダイアグラム.[1]より抜粋。
上図はNPのグラフィカルモデル(a)と計算ダイアグラム(b)になります。観測データ\(C\)の情報を一つの隠れ変数\(z\)に集約していることがわかります。そして,\(z\)と未観測データのインプット\(x_{new}\)から、\(y_{new}\)を予測しています（図での添字はnewではなくTです）。\(x\)が無ければ、Variational AutoEncoder(VAE)と同じ構造をしていることが分かります。
図(b)を見ると、計算のフローとモデルの構成がより分かりやすいです。
- 観測データ\(C=\{(x_{i}, y_{i})\}_{i=1}^{m}\)を表現ベクトル\(\{r\}_{i=1}^{m}\)にエンコーディングする。\(r_{i}=h(x_{i}, y_{i})\)にNN関数を使用。
- 表現を一つに集約する。ここでは平均関数を用いる。\(r=a(r_{1:m}) = \frac{1}{m}\sum r_{i}\)
- 隠れ変数\(z\)はガウシアンであり、平均と標準偏差は\(r\)の関数から計算。\(z \sim N(\mu (r), \sigma(r)I)\)です。
- 隠れ変数\(z\)と\(x_{m+1:n}\)から\(y_{m+1:n}\)を計算。\(y_{i}=g(z, x_{i})\)はNN関数を使用。
モデルの目的関数は対数尤度の変分下限で、以下の式が最小となるようパラメータを逐次更新します。
NPのEvidence Lower Bound. [1]より抜粋。
モデルの訓練は以下のとおりです。
- 学習データを\(C\)と\(T\)にランダムに振り分ける。それぞれの個数も一定でなくてもよい。
- 変分下限を減らすようパラメータを更新。
- 1,2を収束するまで繰り返す。
デモ
NPの性能を簡単な例で検証してみたいと思います。Pythonのバージョンは3.6.5、DL用のフレームワークはPytorch1.4.5を用いました。実装コードはgithubに置いてありますので、ご参考ください。また、本ブログの不明点、間違いの指摘がありましたらissue上で問い合わせください。GPの場合と同様に,\(y=sin(x)\)を目的関数として予測すること考えます。訓練用データには\([-4, 4]\)の範囲内で一様にサンプルした10点を用います。モデルの構成は、エンコーダー、デコーダー共に隠れ層が8次元の一層からなり、隠れ変数\(z\)の次元は4次元としています。
学習した結果はFig.2のとおりです。
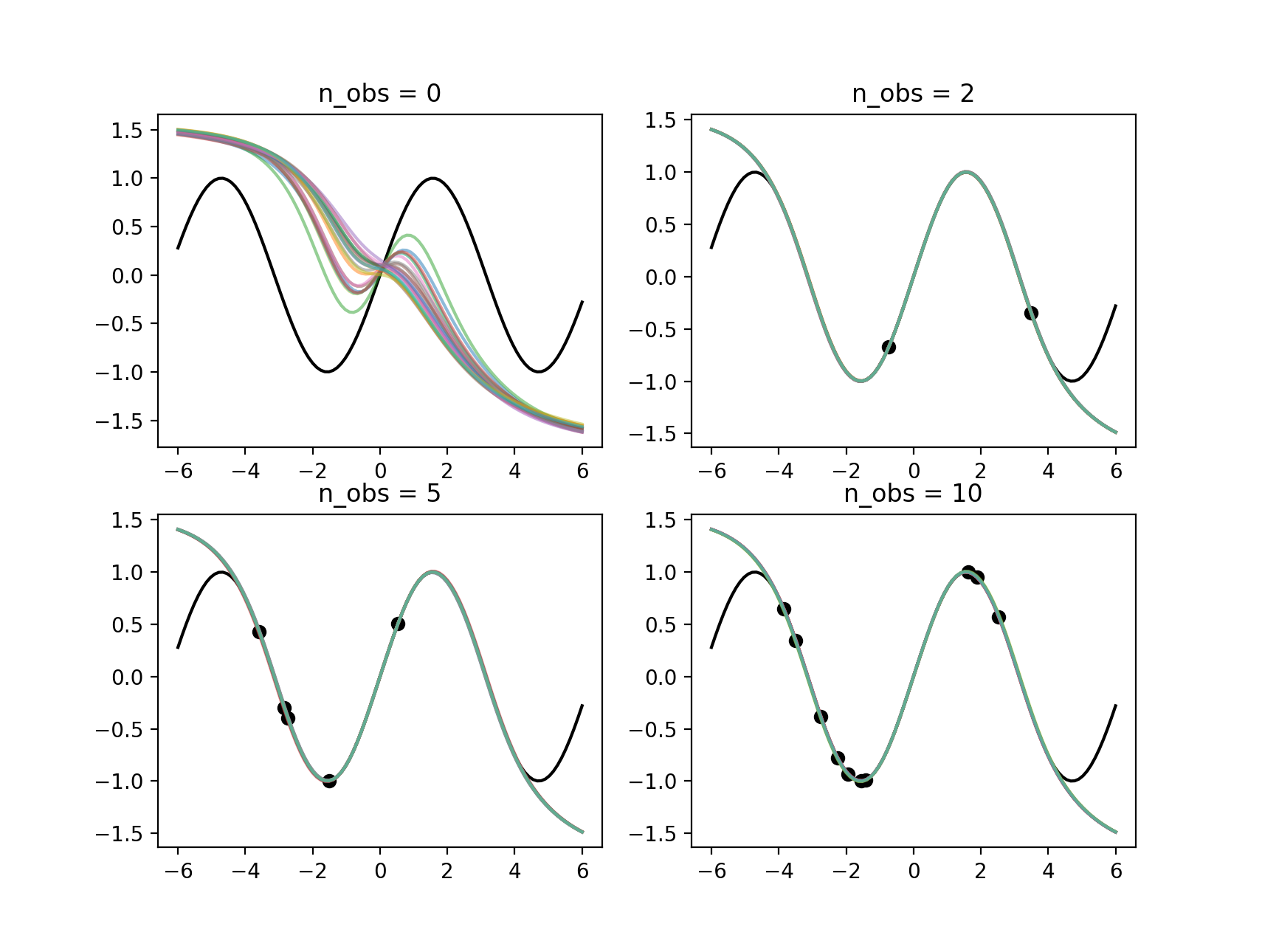
Fig.2: NPによるsin(x)の学習。観測点ごとに並べた。
観測データとして0, 2, 5, 10点与えたときの予測された関数のサンプルを色付きで示しています。n_obs=0のときはは事前分布からサンプルになりますが、\(sin\)関数の形状を捉えている様子が分かります。2点与えた場合でも目標となる関数と完全に一致しています。観測データを与えた場合、サンプルされる関数の分散はゼロで目標とする関数に完全に一致します。さらに観測点が１点の場合(Fig.3)も見てみましょう。
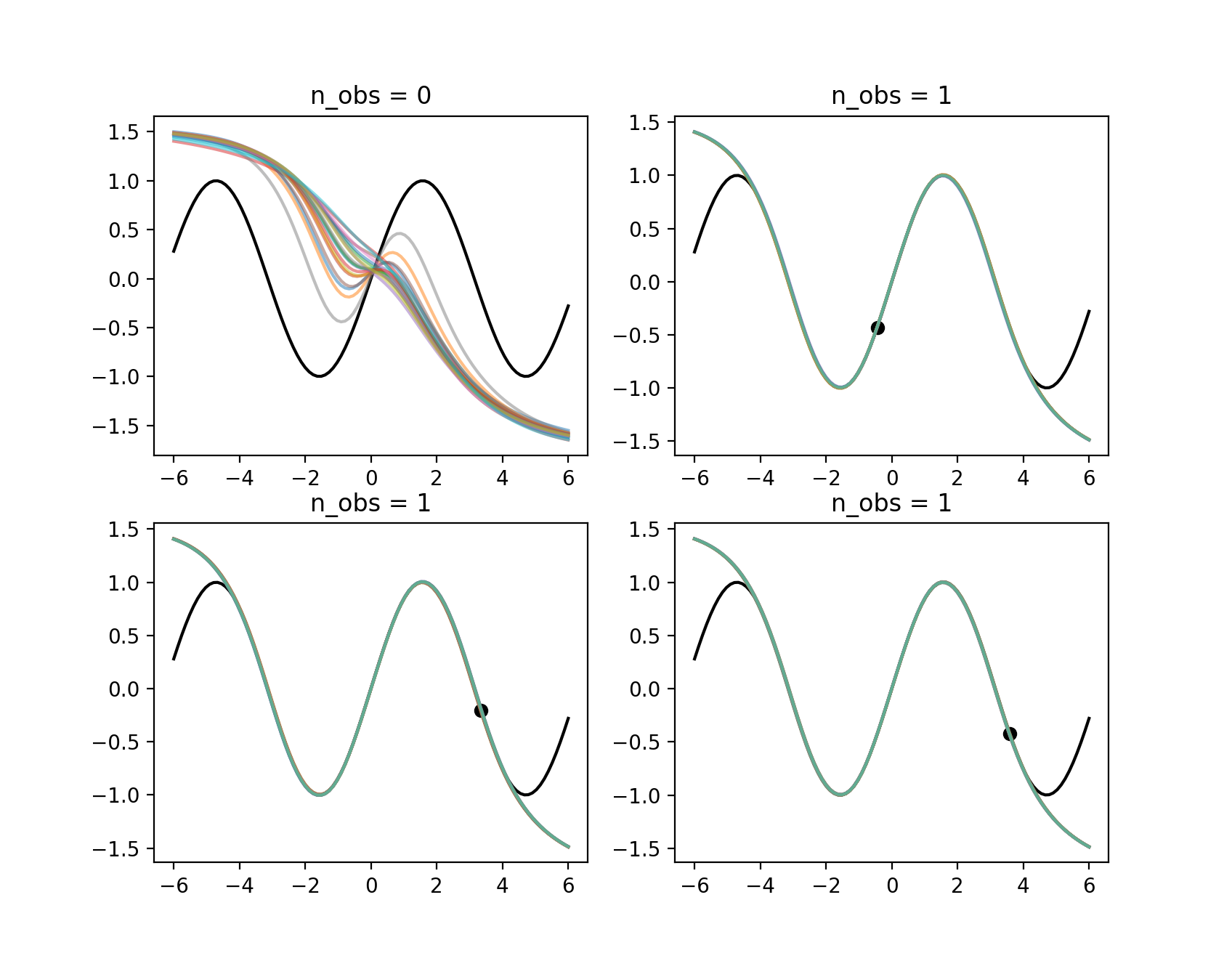
Fig.3: NPによるsin(x)の学習。観測点が一点の場合。
一点でも十分であることがわかります。訓練時のデータは\(X \in [-4, 4]\)$なので、両側の外が一致しないのは自然です。しかし、GPで見られるようなばらつきが見えません。観測点から離れた領域ではある程度ばらつきが見えると想定していたので、これは意外でした。GPと異なり、事前分布はNN関数の学習によって決まるため、今回のような単一の関数から得られる学習データの場合、未観測の領域も観測データに引きづられて単一の関数形に収束すると考えられます。エンコーダーのウェイトの初期値により分散の大きい乱数を使用する、層を重ねてより複雑なNN関数を使うといったことをすれば、未観測領域に対する信頼度をGPのように反映できる可能性があります。
次に、関数空間に対する分布をNPが再現できるかについて確認します。ここでは、ランダムに関数が変化する状況を想定します。学習データを次のように生成します。
- \(x \sim Uniform([-4,4], n=10)\)
- \(a \sim Uniform([-2,2], n=1)\)
- \(y = a * sin(x)\)
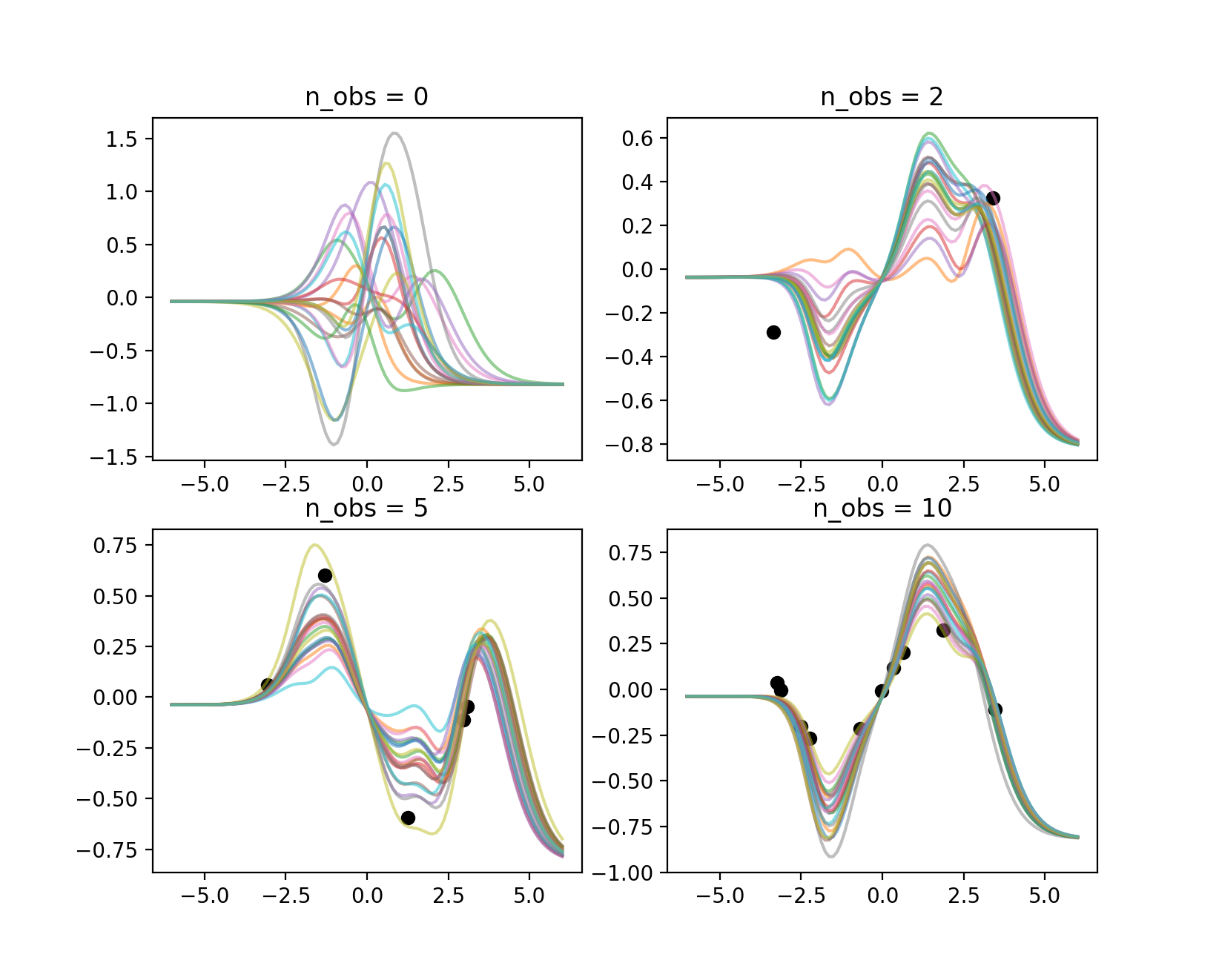
Fig.4.: NPによるa*sin(x)の学習。観測点ごとに並べた。
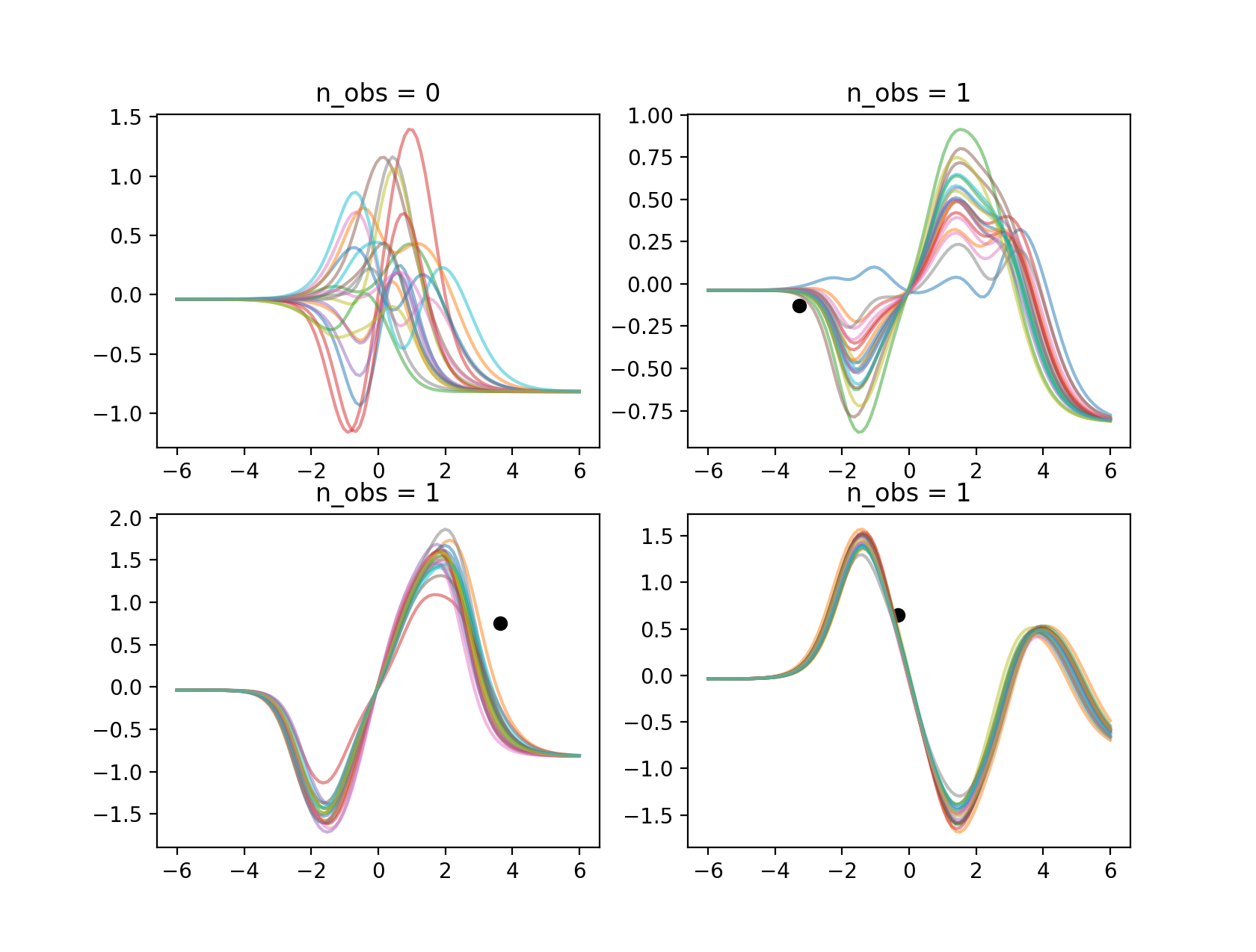
Fig.5: NPによるa*sin(x)の学習。観測点が一点の場合。
結果を見ると、１点与えたときでも、元のサンプルデータに含まれる関数の形状を十分再現していることが分かります。また、点の位置によって、関数がばらつき方が異なることが分かります。Fig.5の右上においては、観測点が係数の\(a\)に依らず関数が通る位置にあるため、一意に特定することが難しく、予測関数にばらつきが見られます。一方、Fig.5の下段の例では、関数形が大体特定できています。観測点が無い場合、つまり事前分布から関数がサンプルされた場合を見ても、学習データを生成する元となる関数形(\(a*sin(x)\)が含まれているように見えます。このように、学習データから暗に入出力を関係づける関数に対する確率分布を学習できたため、少ない観測点でも正確な関数形を特定できるようになったと言えます。GPを使っても、このような結果にならないのは上の例で確認したとおりです。
まとめ
以上、簡単にまとめると次のようになります。- NPは確率過程にNN関数を適用した確率的生成モデル。古典的なGPと比べて、モデルの表現力とデータに対するスケーラビリティが向上。
- NPでは、GPと異なり学習が必要。生成される実データが従う関数の分布を反映した分布を学習可能。少ないデータ点で、正確な予測関数の事後分布が得られる（few-shot learning）へ応用可能。
- GPの予測値の分散は観測値付近で小さく、離れつにつれて大きくなる傾向にある。しかし、NPでは観測値以外の領域でも分散がほぼ無くなる傾向にあり、望ましい性質ではない。構造が近いVAEでも同様の問題が起こりうることが知られており（KL Collapse)、改善の余地がある。
最後に。次世代システム研究室では、アプリケーション開発や設計を行うリードエンジニアを募集しています。アプリケーション開発者の方、次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
