2017.01.17
再帰型強化学習を用いた金融商品取引の可能性
次世代システム研究室のL.G.Wです。今回も、前回から引き続き強化学習のトピックを話します。今回は、Direct Policyベースの再帰型強化学習の特徴を解説し、FXの自動取引を例にして、実装およびその結果を説明します。
再帰型強化学習とは
強化学習(前回のBlogを参考してください)には、大まかに2種類のアプローチがある。一つは、Value関数の近似化。典型的なアルゴリズムはQ-Learning (有名事例:Play Atari)である。もう一つは、最適なPolicyを直接探索する手法。世の中に大きな衝撃を与えたAlpha GoもこのDirect Policy手法を利用した。
二つの手法の類似点は、(1)環境へActionを起こし、そのActionで得られた報酬を学習信号として、ActionのPolicyを修正し最適なActionを取れるルートを学習する;(2)Supervised Learningと違って、基本的には最適結果は一つ状態での最適Actionではなく一連のActionに左右される。つまり、結果がActionパスに依存する。
一方で、相違点もある。(1)Valueベースの手法は、すべての状態空間とAction空間をランダムに再現し、その上に最適なValue関数を近似化する。そのため膨大な計算量になり、現実的でない空間を探索する可能性がある;一方、Policyベースの手法は、この中間StepのValue関数をバイパスし最適Policyを直接求めるので、最適探索はより効率化だと考えられる。(2)Valueベースの手法はDelayed報酬を考慮しているため、ゲームやチェスのような問題に向いている(Actionの度に報酬が出るわけではないし、瞬時報酬が最大化しても意味がない);一方、Policyベースの手法は、Immediate報酬だけを考慮することが多い(ただしAlpha GoはDelayed報酬)。単一金融商品(株、FX)の取引ならImmediate報酬がすぐ分かるし、毎回の取引の報酬が最大化すれば最終報酬も最大化になるのでPolicyベースの手法は適用できる。(3)Valueベースの手法は、MDP(厳密に言うとPOMDP)で定義できる問題なら同じ計算ルーチンで求められるが、Policyベースの手法の場合、対象問題によってはPolicy Gradientの定義が困難である。
今回は、こちらの論文(1, 2, 3)を参考しながら、Direct Policyの再帰型強化学習をFX取引に応用してみた。なぜRecurrent(再帰型)と呼ばれるかというと、現状態のActionの予測のために、前状態のOutput(Action)をInput情報として使用しているためである。
補記:Valueベースの強化学習をFX取引に応用した例は、弊社のBlogで紹介された。ただこの論文によると、Recurrent Reinforcement Learning (RRL)がQ-Learingより性能がよいという検証結果が示されており、今回のRRL検証の動機になっている。
FX取引のモデリング
それでは、この再帰型強化学習(Recurrent Reinforcement Learning)をどうやってFX取引に応用するかを解説する。以下の定義はFXだけでなく、ほかの金融商品、例えば株やオプションにも応用できる(ただし単一Assetのみ、つまりPortfolio管理は考慮していない)。
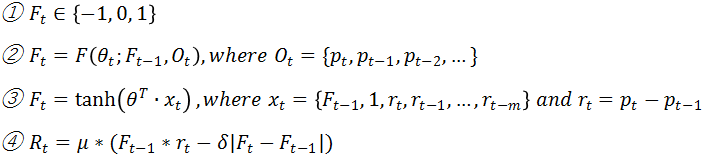
式①は取引(Trade)のAction空間の定義である。F_tは時刻tで取るActionで、1はLong(買い)、0はNeutral(ポジションクローズ)、-1はShort(売り)である。もし時刻tに1、時刻t+1も1なら、これは時刻tの買いPositionを持ち続けことになる(連続の買いではない)。もし時刻tは1、時刻t+1が0なら、時刻t+1に買いPositionをクローズする(= 売る)。もし時刻tは1、時刻t+1が-1なら、時刻t+1に時刻tの買いポジションをクローズし(= 売り)、さらに売りポジションを取る。
今回の目的は式②に定義した通り、ある時刻に観測した環境状態とその前時刻で取った取引ActionをInputとする、関数Fのパラメータθの最適値を見付け、時刻tでの最適取引Actionを求めることである。ここでは、観測状態は過去のある時点から現在までの為替レートだけを考える。関数Fはどのような関数でも良いが、数学的に扱いやすいTanh関数にする。このとき、式②は式③に置き換えられる。ただ式③はOutputが[-1, 1]間の連続数値なので、そのOutputに符号関数を掛けて、{-1, 0, 1}に変換する。Inputベクターx_tは為替レートの生数値ではなく、単位時間のレート変化量を取り込んでいる。また1番目の要素は、前時刻の取引Action F_t-1であり、2番目の要素は定数1である(バイアスに相当)。式④は時刻tの報酬(またはReturn)を定義している。μは売買可能な最大数量(例えば1万通貨、1万株)である。δは最小売買単位に掛ける手数料(FXの場合はSpreadと呼ぶ。例えば、0.3銭/ドル)である。この式を見ればわかるように、もしF_tとF_t-1が同じであれば手数料は発生しない。つまり同じ数量μをさらに買い(売り)するのではなく、前のPositionを維持するだけである。
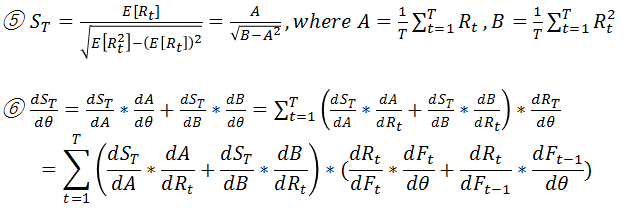
今回の目的関数(Utility)は上記の式④ではなく、式⑤に定義したSharpe Ratioである。Sharpe Ratioはリスクを考慮したReturnである。元論文は、Differential Sharpe Ratioを提案しているが、今回はSharpe Ratioを利用した。目的関数のθの微分を求めることで、普通のGradient Descent方法でParameter θを最適化することができる。式⑥は、このGradientの計算式である。
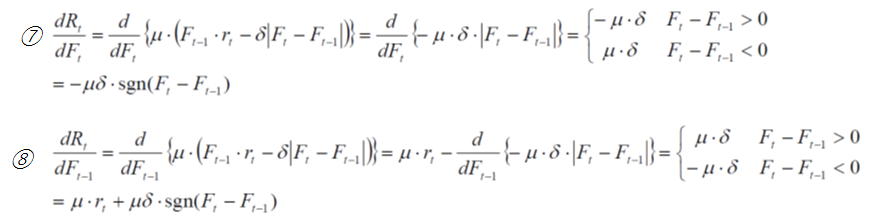
さらに式⑥に含まれるdR_t/dF_tとdR_t/dF_t-1は、それぞれ式⑦、⑧により算出される。
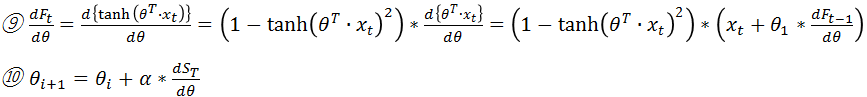
dF_t/dθは式⑨で計算される。以上の式を統合することで、目的関数対Parameter θのGradientは、Inputベクターx_t(前状態の取引Actionと観測したレート)から算出することができる。式⑩を反復計算することで最適なParameter θを決定する。最適なParameter θが分かれば、式③より最適な取引Actionが得られる。これがDirect Policyの強化学習である。
実装
今回はR言語で実装してみたが、まだまだ改善箇所(バグがあるかも)が多いので(とりあえずソースを公開せず)基本的な流れと重要な関数だけを説明する。
まずTraining関数だが、以下のようにFull BatchのGradient Descentで実装してある。
training <- function(length){
weights <- rnorm(length+2, 0, sd=1.0)
for(epoch in 1:MAX_ITERATIONS){
trade.vec <- tradeVector(weights, length, nPoints)
sharpeList <- sharpeRatio(trade.vec)
sharpeRatio <- sharpeList[[1]]
if(sharpeRatio > 0.15 && epoch >= 500)
break;
spGrad <- sharpeGradient(weights, length, trade.vec)
weights<- weights + LEARNING_RATE * spGrad
}
weights
}
Parameter Lengthは、Inputデータ:レート時系列の期間である。tradeVectorは式③がベースで、tanhの絶対値が0.7を下回ると0に変換する;0.7以上なら符号関数を使って1或いは-1に変換する。sharpeRatio関数は式⑤そのものである。sharpeGradientは式⑥、式⑦、式⑧、式⑨の計算式を統合したもので下記のコードを参照。その中のtradeGradientは式⑨そのものである。
sharpeGradient <- function(weights, length, trade.vec){
tGrad <- tradeGradient(weights, length, trade.vec)
sharpeList <- sharpeRatio(trade.vec)
A <- sharpeList[[2]]
B <- sharpeList[[3]]
R <- sharpeList[[4]]
# S = A / sqrt(B-A^2)
dS_dA <- (B - A^2)^(-1/2) + A^2 * (B - A^2)^(-3/2)
dS_dB <- (-1/2) * A * (B - A^2) ^ (-3/2)
dA_dR <- 1 / nPoints
sharpeGradient <- matrix(0, nPoints, length+2)
for(i in length:nPoints){
#dB_dRi <- 1 / nPoints * 2 * rPrices[i] #Rt????
dB_dRi <- 1 / nPoints * 2 * R[i]
dRi_dFi <- -MAX_SHARES * PRICE_SPREAD_COST*sign(trade.vec[i] - trade.vec[i-1])
dRi_dFi_1 <- MAX_SHARES * (rPrices[i] + PRICE_SPREAD_COST*sign(trade.vec[i] - trade.vec[i-1]))
sharpeGradient[i,] <- (dS_dA * dA_dR + dS_dB * dB_dRi) * (dRi_dFi*tGrad[i,] + dRi_dFi_1*tGrad[i-1,])
}
apply(sharpeGradient, 2, sum)
}
実験結果&検討
今回はこのサイトが提供している為替レート(Tick)を利用して実験を行った。
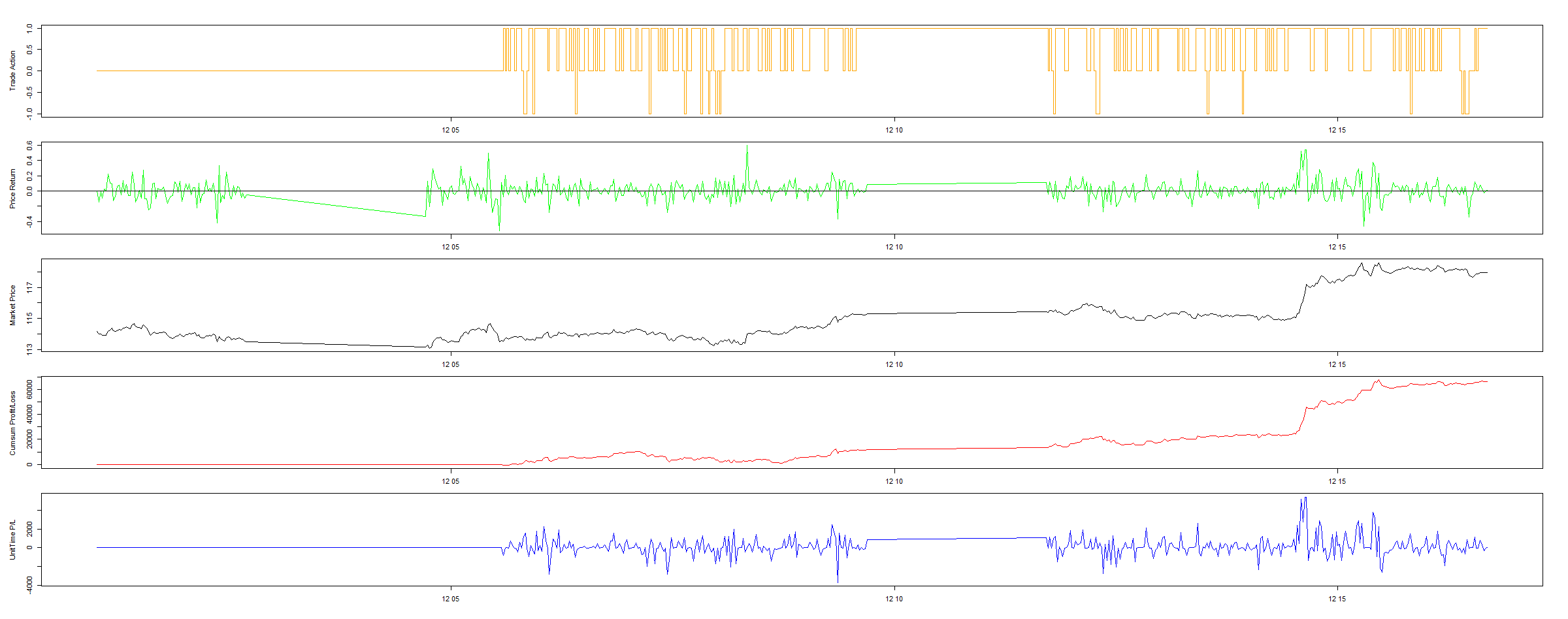
上図は11月のUSD/JPYのレート(Tick=30分)を学習して、12月1日から12月16日まで検証した結果である。手数料(Spread)を0.3銭に設定し、取引数量は1万ドルを固定してある。図1(Trade Action)は検証期間のLong・Short・Neutralという取引動作を示してある。図2(Price Return)はTick毎のプライス変化量を示してある。図3(Market Price)はUSD対JPYのレートを示してある。図4(Cumsum Profit/Loss)は累積評価損益を示してあり、最終損益は約6万円である。図5(Unit P/L)は単位時間(30分)の評価損益を示している。
次に手数料を3銭(上記の10倍)に設定すると下図のような結果になる。手数料が大きくなったことで、取引回数が減っていることがわかる。当然、収益も減少傾向にある(前回の半分で約3万円になる)。

下図は、学習期間のSharpe率(Utility)が学習回数(Epoch)と共に変化していることを示している。三つの図はそれぞれ違う初期値、または違う期間での学習結果である。たしかにGradient DescentでSharpe率が増えていることを確認できるが、時々下がっていることもあり、プログラムの正確性をさらにチェックする必要性がある。
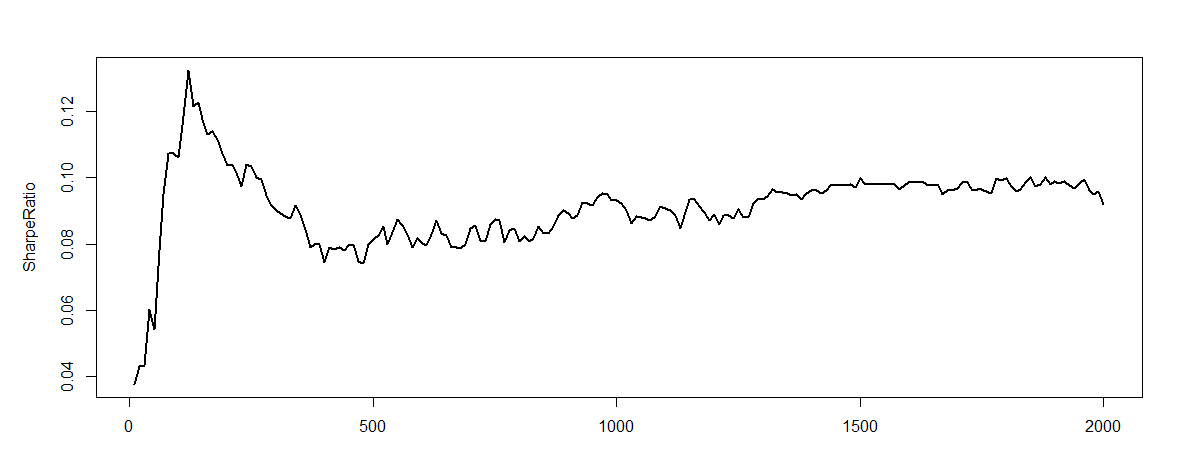
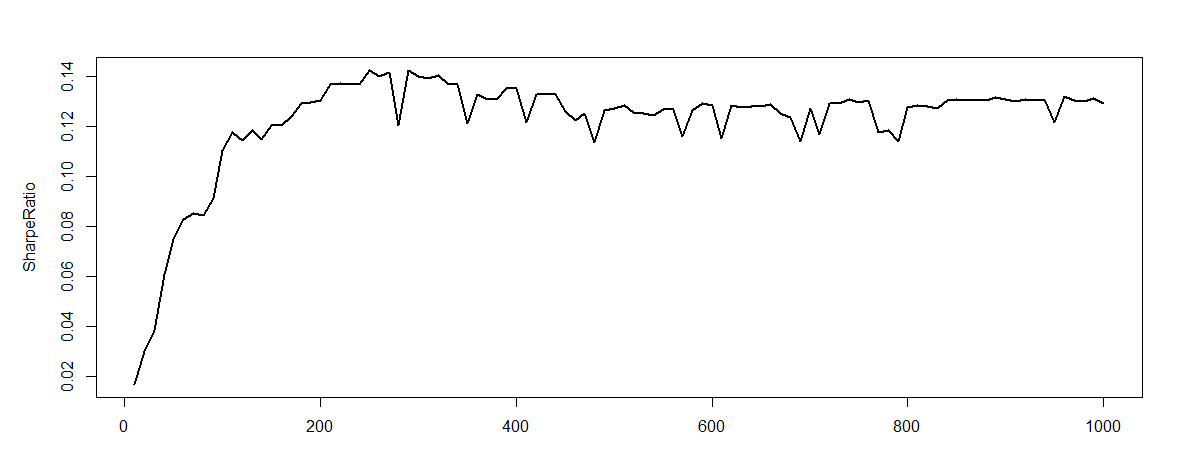
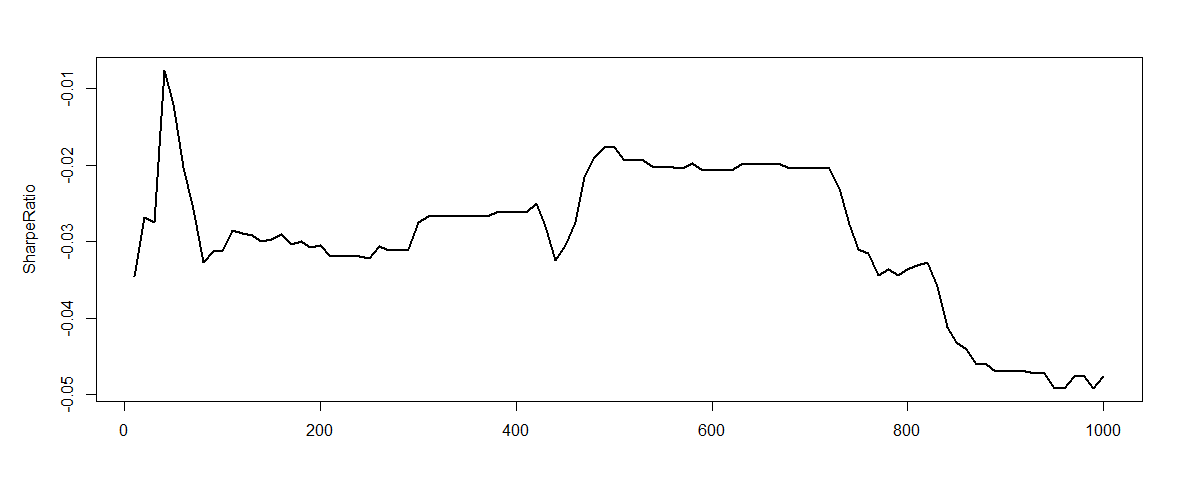
今回の簡単な検証によれば収益が出ており、再帰型強化学習のFXへの応用に期待が持てる。また今回は深層学習ではなく、Market PriceをTanhの1層で変換しただけだった。もしDeepなネットワークを構築すれば、より良い結果が出るのではと期待できる。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD