2018.04.04
UC Berkeleyの深層強化学習コース(CS294)のまとめノート
次世代システム研究室のL.G.Wです。今回は、最近勉強したUC Berkeleyの深層強化学習コースを纏めて紹介させていただきます。コースの講義内容は、UC Berkeleyのウェブサイトで公開され、さらにレクチャビデオもYoutubeからアクセスできます。コース全部は24コマですが、ここでは、下記のアウトラインに示した章節に分けて解説します。
アウトライン
- 強化学習の定義、目的関数、基本構造、各種アルゴリズム
- Policy Gradientベースのアルゴリズム
- Actor-Criticモデル
- Value関数ベースのアルゴリズム(Value function)
- Advanced Q-learning
- モデルベースのアルゴリズム(Model-based)
- 模倣学習(Imitation Learning)
- 逆強化学習(Inverse Reinforcement Learning)
- 探索と活用のトレードオフ(Exploration and Exploitation)
- 転移学習(Transfer Learning and Multi-task Learning)
- メタ学習(Meta Learning)
マルコフ決定過程の視点から強化学習の概念とNotationを定義し、ゴールと基本構造も解説し、さらによく利用されるアルゴリズムを軽く触れる。
Policy Gradientを利用し、強化学習のゴールにどう至るか。この方法の欠点(High Variance)と改善対策(Importance Sampling)。
Policy Gradientの欠点を克服するため、Critic役を導入する。Actir-Criticモデルのアルゴリズム詳細と応用。
Value関数のみを学習して、状態のValueからPolicyを決定すると、どうなるか?
深層ニューラルネットワークを活用し、状態と動作のQ値を学習する。学習性能改善のトリックも。
状態遷移のダイナミクスをモデリングし、そのモデルからPolicyを決定する強化学習方法。
Expertの行動を効率よく学習する(Guided Policy Search)。
Rewardを明確に定義できない場合、Reward自体を学習する。これを逆強化学習と呼ぶ。
Multi-arm BanditやPosterior Matchingなどを利用することで、より良いRewardを得られる。
転移学習を用いてニューラルネットワークの一部を再利用することで、一つドメインで学習したPolicyを複数ドメインで共有する
学習のコツを学習するのは、メタ学習。(Learning to learn)
今回は、最初の4章を紹介し、残った内容は、次回発表する予定です。
強化学習のイントロ
定義
強化学習は、Markov Decision Process(MDP)により、厳密に定義された。MDPには、四つの要素から定義される:(1)S=状態空間、(2)A=動作空間、(3)T=状態遷移確率、(4)r(s_t, a_t)=報酬関数。実世界には、状態を直接計れい問題も存在する。あるシグナルを観測して状態を推定すること、Partitially Observed MDPと呼ぶ。POMDPには、さらに2つ要素が定義される:(5)O=観測空間、(6)E=ある状態からシングルを観測できる確率。
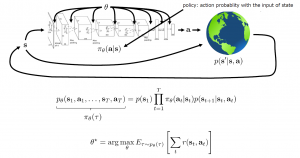
強化学習は、その上にPolicyを追加する。Policyとは、ある状態において、最適な動作を決める関数である。下図は、強化学習のプロセスを示してある。
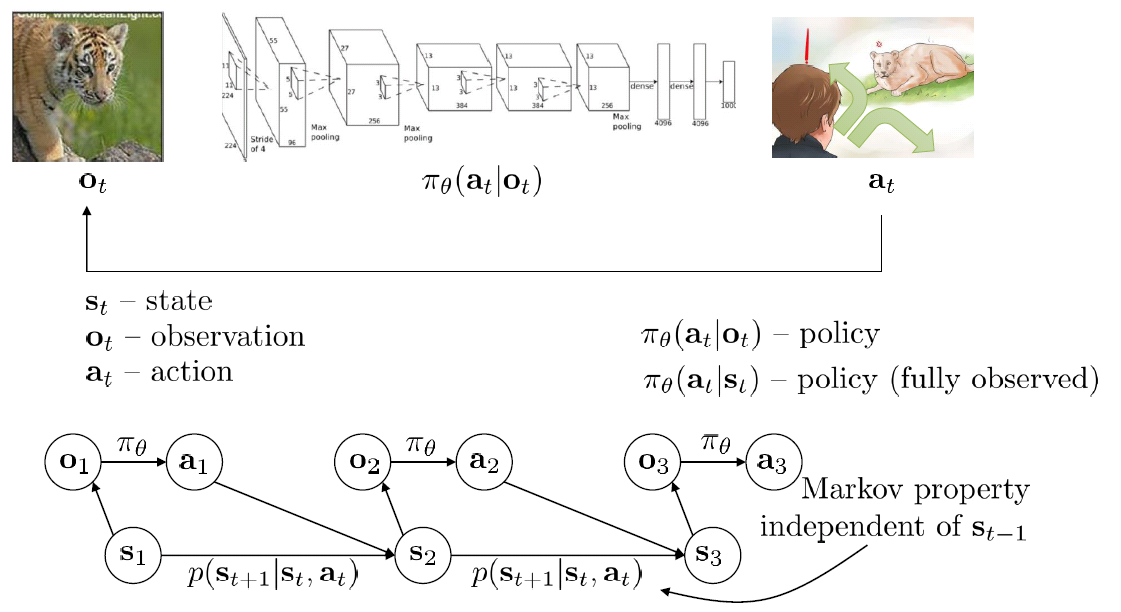
強化学習は、アルゴリズムにより、このPolicy関数(π(a_t|s_t))、或いは状態の値関数(V(s_t))、或いは状態のQ値関数(Q(s_t, a_t))、或いは状態の遷移ダイナミクス(P(s_t+1|s_t)を最適化するプロセスである。それらの関数を表現するのは、よくDeep Neural Networkを用いて近似する。なるべく近似できるような最適化方法は、やはり勾配降下法である。
ゴール
あるPolicyに基づき、状態s_tに動作a_tを選択し、次の状態s_t+1に遷移して、またPolicyで次の動作a_t+1を決める。これを繰り返して、学習データを構築する。このプロセスは生成モデルのように、下記の式で確率分布として定義される。
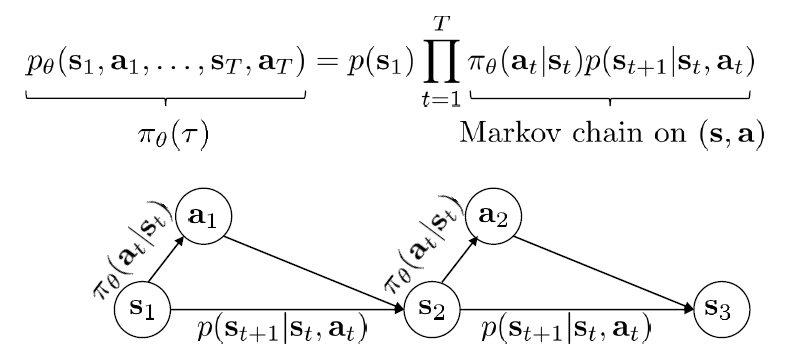
強化学習のゴールは、上記の分布に従うデータを学習し、報酬を最大化するために、上記の分布のParameterを近似すること。下記の式は、強化学習の直接目的関数になる。
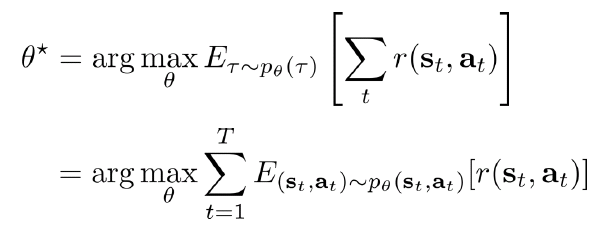
アルゴリズム
学習アルゴリズムは、大体4つに分類される:
(1)Policy Gradient:上記の目的関数を直接微分してPolicyを求める。
(2)Value関数:状態の値関数、又は状態と動作のQ値を推定する。(明確なPolicyを作らない)
(3)Actor-critic:上記(1)と(2)の組み合わせで、Value関数を推定し、それを用いて、Policy関数を改善する。
(4)Model-based:状態間のダイナミクス(遷移確率)をモデリングし(つまり、環境を学習する)、そのモデルのParameterを推定した上で、Policy関数を改善する又は最適計画に直接使う。
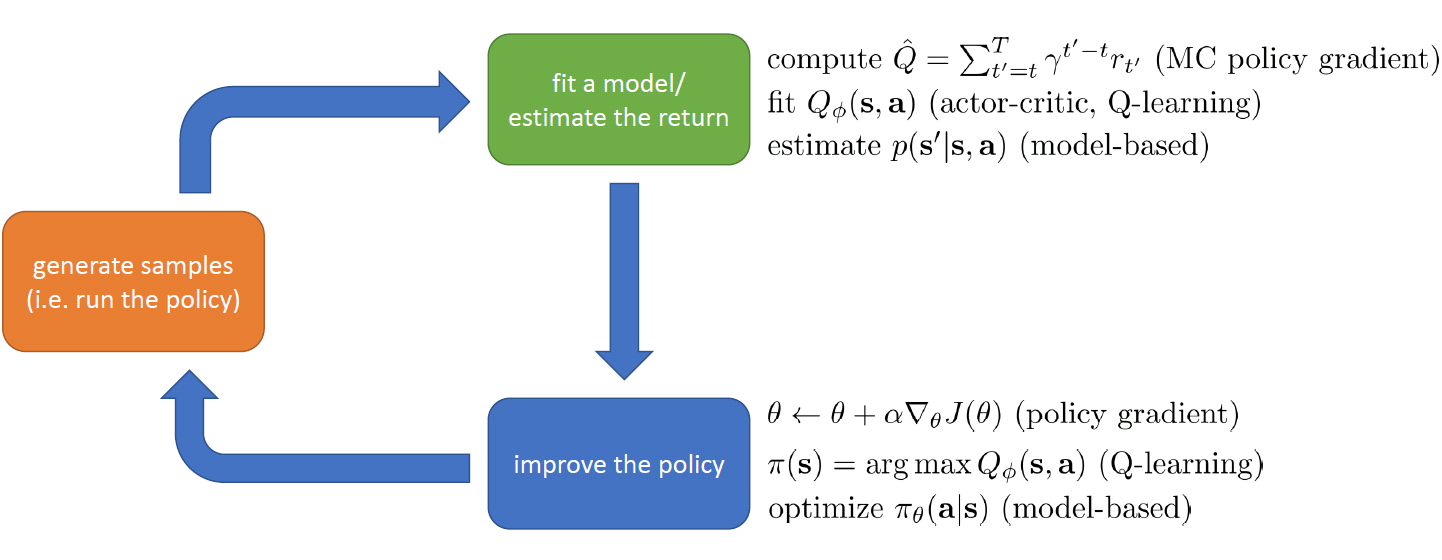
応用課題の環境制限や応用目的により、それぞれの長所短所がある。例えば、学習サンプルの数、状態又は動作が連続か離散か、安定性と使い易さなどにより、トレードオフをとるべき。だが、どのアルゴリズムでも、学習過程は、上図のフレームワークに当てはまる。この過程は、再帰的で、あるPolicy関数で動作を決めて繰り返して、サンプルを生成する(Simulationの場合もある)、上記の4つアルゴリズムによりParameterをFittingし報酬を推定する、そして推定した情報(成績)からPolicy関数にFeedbackし、Policy(暗黙又は明確)を改善する。
Policy Gradient
Policy Gradient法は、一般の教師あり学習と類似して、目的関数の微分(Policy Gradient)を計算し、このGradientに沿ってPolicy関数のParameter(θ)を最適化する方法である。下図のように、目的関数(またはコスト関数)J(θ)を微分し、右上の同値Equationを代入して、微分式をLog方式に変形する。Log関数になると、積算を足し算になることで、計算が大変容易になる。

アルゴリズムは下記に示したように、Policyを執行し、一つのサンプル(Episode、ゲームの場合なら1試合)を生成する。そして、Policy Gradientを(2)の式で算出する。さらに、勾配降下法の原理で、Policy関数のParameter(θ)を更新してから、また(1)を繰り返す。
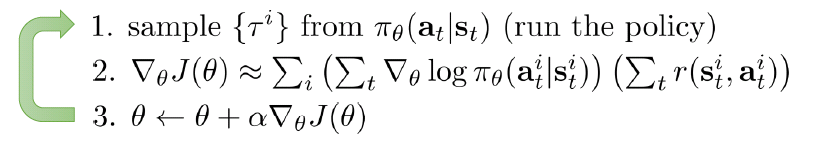
このアルゴリズムはシンプルだが、一つ一つのサンプルで学習し、Parameterを更新するので(On-Policyと呼ぶ)、Gradientにノイズが大きくて、Varianceが高くなり、収束が遅いだけではなく、学習レートによっては、収束しない恐れもある。この欠点(High Variance)を解決するため、下記のようにBaselineの平均報酬(b)を引いて、Varianceを減らすことができる。さらに、この平均報酬(b)は、Policy Gradientの最適化の過程で期待値がゼロになるため、同じゴールに到達することも保証される。
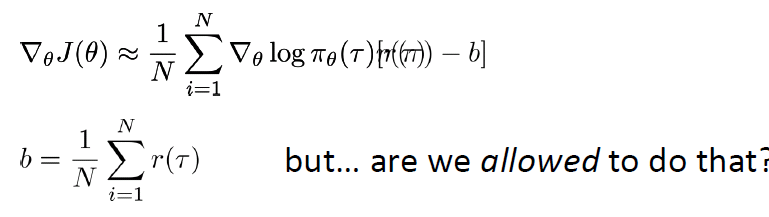
以上を踏まえて、一つのサンプル毎にPolicyを更新するのは、学習効率が悪く、ノイズもまだ高いので、Off-policyでのBatch方式の学習が考案された。既存θのPolicy関数(π_θ)の上に、別のパラメータ(θ’)のPolicy関数を定義し、Importance Samplingの原理から、下記のように目的関数を変形する。そして、Policy π_θを固定して、Batch方式(大量Sample)でPolicy π_θ’をFittingする。その後、Policy π_θ’を固定し、Policy π_θを更新する。この過程を繰り返して、収束していく。
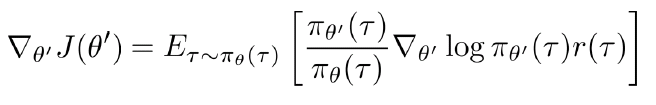
Actor-Criticモデル
Actor-Criticモデルを紹介する前に、状態及び状態-動作のValue関数を定義する。下記のQ関数は、状態s_tから終了まで取得できる報酬である。下記のV関数は、Q関数の同時周辺分布で、つまり、動作a_tと関係せず、状態s_tのみに依存するすべての動作の平均報酬である。下記のA関数(Advantage関数)は、特定動作a_tを選んだ場合、平均報酬よりどのくらい優位差があるか、つまり、Q関数とV関数の差である。そして、前節のPolicy Gradientに定義した目的関数(J(θ))をA関数で置き換える。この場合は、V関数は前節のbに相当することになる。

上記の目的関数ならば、強化学習のゴールは、なるべくA関数を近似することになるが、実際は、V関数をNeural Networkでよく近似することでゴールに達成できる。なぜならば、下記の式に示したように、V関数が分かれば、Q関数が求められる。さらに、A関数もQ関数とV関数の差なので、V関数が分かれば、A関数も求められる。
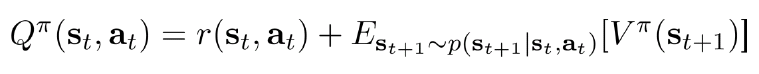
上記の目的関数(A関数を含める)は、動作の良さ悪さを評価するので、Criticの役割であり、Policy πに基づき、動作を執行するのはActorと呼ぶ。
最終的に、Actor-Criticモデルは下記のアルゴリズムで実現する。バッチモードは、一回複数サンプルを生成し、それらのサンプルの報酬からVφ(s_t)をNeural Networkで近似する。さらに、未来の報酬は、現在の状態と動作に反映すべきではあるものの、割引係数で計上するのは合理的なので、Step 3のように、A関数を計算する。そして、目的関数(コスト)を計算して、微分でPolicyパラメータθを更新する。

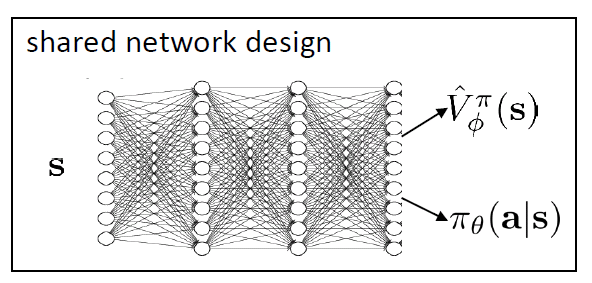
Actor-Criticモデルは、Vφ関数とPolicy π_θを学習するため、それぞれ二つのネットワークで近似するのは、シンプルかつ安定である。が、この二つの関数を一つのネットワークでShareし、最終Outputで振り分けて学習するのは、より効率的である(下記のネットワーク構造)。さらに、この二つの関数を非同期で並列学習するのは、最新のメインストリームになっている(著名なA3Cモデル)。
未来の報酬はすべて現在状態のV関数に影響するので、Varianceが高くて、収束が遅くて、精度が低い。それを改善するため、下記のように、A関数を、n stepまでしか計上しないようなアルゴリズムが提案された。
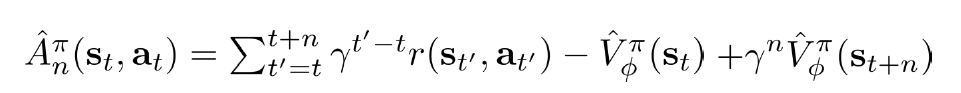
Value関数法
まずは、A関数の定義を振り返る:A(s_t, a_t)はPolicy πに従い、動作a_tがほかの動作よりどのくらい有利な報酬が得られるかを表す。もし、A関数が分かれば、下記のルールでPolicy π’を作れば、必ず元Policy πより、よい動作(トータル報酬が高い)を決めることができる。そうすれば、Policy πを求める必要はなく、Policy Gradientを忘れても良い。その場合、A関数を求める必要があるが、前節にも述べたように、A関数はV関数を通して計算できるので、結局、V関数のみ近似すれば、Policy πが明確に求められなくてもいい、ゴールに到達するわけ。これを、Value関数法と呼ぶ。
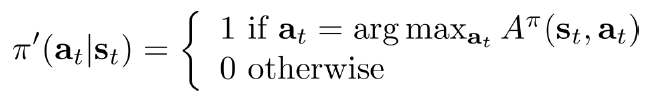
Value関数法は、もし状態遷移p(s’|s_t, a_t)が分かれば、基本的に下記に示したように、Dynamic Programming法でVとπ’を解くことができる。これを、Policy反復法と呼ぶ。

また、下記のように、Q関数を現在状態の報酬と未来状態のValue関数から計算し、Q関数のMax値をValue関数に代入といったように反復計算して解を求める方法を、Value反復法と呼ぶ。
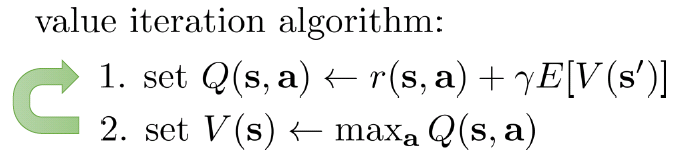
実は、もしQ関数を近似すれば、Value関数の学習も行わずにすむ。これを、Q関数反復法(又はQ-learningと呼ぶ)。下記のように、Q関数のφを最適化するため、収集したサンプルから、現在のQ_φを利用して、yを計算し、現在状態のQ関数とyの差をなるべく小さくする。

Q関数法の良い点は、サンプルが現在のPolicy πに依存しないことで(Off-Policy)、サンプルの生成とQ関数の学習を切り離せるため、バッチ学習や並列学習に適します。
また、上記は、Q関数をFittingする方法で近似化するが、下記のように、Q関数の微分でParameter φを近似化していく方法もある。ただ、これは、目的関数の微分ではないので、Gradient Descentとはいえない。それでも、Value関数の学習理論により、Q関数の微分でも確実にParameterの学習が収束していくことが証明されている。

Value関数法(Q-learningも含め)には、Policy πが、いつも最大の値を取るように、動作を決める。しかし、それには一つ大きいデメリットがある。要するに、一時的又は最初時点で報酬が悪い動作は、ずっと選ばれないため、探索範囲が限られる。それを解決するため、下記のように、εの確率(小さい数値)で最大報酬ではない動作もランダム選択する。又は、動作a_tの確率は、Q値の指数関数に比例する。つまり、動作a_tのQ値が高いほど、選択される確率が高い、ただし、確実ではない。
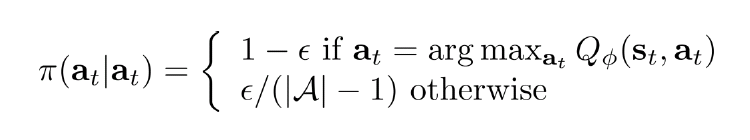
今回紹介する内容以上で、次回は高度なQ-learning手法を始めとして、より最新な内容を解説します。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD