2016.10.05

強化学習（Reinforcement Learning）とRL4j

次世代システム研究室のL.G.Wです。今回は、強化学習の原理と、それを実装したRL4jというFrameworkについて紹介します。

強化学習（Reinforcement Learning）

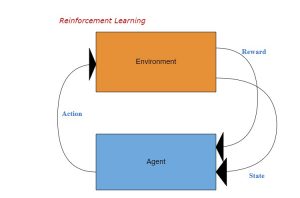
強化学習（Reinforcement Leanring）は機械学習（Machine Learning）の一種で、エージェントが最大の累積報酬を得られるように、ある環境に最適な行動を学習します。ゲーム理論、自動制御理論や情報論などの分野においては、よく研究されてきました。最近Google AlphaGoの活躍のお陰で、強化学習は人工知能においてもその応用が注目されています。

強化学習は、教師あり学習（Supervised Learning）と異なり、ラベルをつける教師データがいらず、環境から得られた平均報酬が学習ゴールになります。教師あり学習が強化学習の一つ特別ケースという考え方もあります。ラベルを報酬とみなし適切にラベル付けすれば高い報酬を得られるよう学習できるので、強化学習のプロセスに似ています。教師あり学習は瞬時報酬（ラベル）しか考慮しないので、分類問題（Classification）には向いている一方、強化学習はDelayed Rewardを考慮し長期的な報酬を得るため、複雑な計画問題（Dynamic Planning）に適してます。

強化学習モデルは以下の要素により構成されています：

    環境の状態空間：S
    行動（Action）空間：A
    行動aを取って、状態sからs’に遷移する時の報酬：R_a(s, s’)
    状態遷移ルール(確率的)：P_a(s,s’)=P(s’|s,a)

強化学習の目的は、どのような環境状態で、最終報酬が一番高いこと。
もし状態空間と行動空間が有限な場合（離散空間）、すべての状態とすべての行動の組み合わせと相応報酬のMappingテーブルを作れば目的を達成できます。もし状態空間が無限の場合（連続空間）、S × A → Rという関数を見つければよいはずです（離散空間にも適用可能）。しかし実際にはSearch空間が膨大で、簡単なBrute Forceでは達成できません。多くの実ケースでは色々な工夫をしていますが、それでも、この最適関数を完璧に求められず近似解を使っています。しかし近似解とはいえGoogle AlphaGoが一流のプロ囲碁棋士を破ったことなどからも、今後はより広く活用されることが期待できます。

Markov Decision Process (MDP)

強化学習で定義した環境は、典型的なマルコフ決定過程（MDP）です。強化学習モデリングすをする際はMDPのことを意識しなくても大丈夫ですが、原理をよく理解するためMDPをまず説明します。

Markov Decision Processは5-tuple (S, A, P_a, R_a, γ)により構成されます。S, A, P_a, R_aは上記に定義した状態空間、行動空間、状態遷移確率、（瞬時）報酬であり、γは報酬のDiscount係数です。つまり、ある時点の報酬はその時点の瞬時報酬とその以後の瞬時報酬を割り引いたものとの合計になります(下記の式を参照)。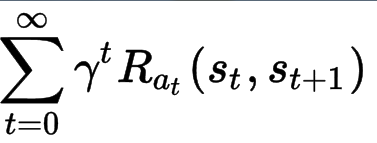total_reward

下図はMDPの一つ例です。三つの状態（S_i）と二つの行動(a_i)があって、行動と状態の間の数値は遷移確率（P_a）を表し、外（環境）へ指している線の上の数値は瞬時報酬(R_a)です。
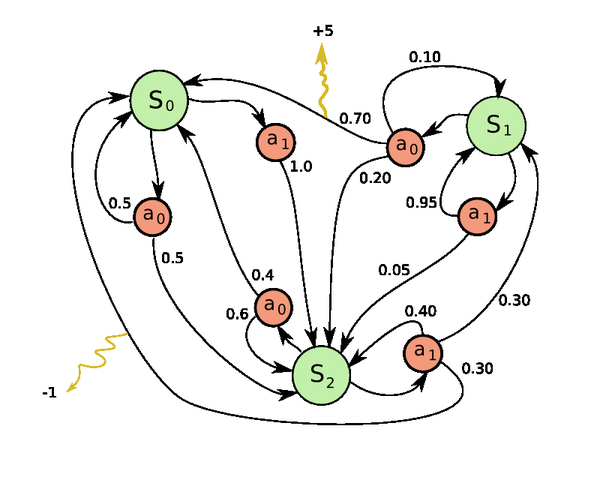
600px-Markov_Decision_Process_example

MDP問題を解くには、以下の二つ方程式を定義します。
方程式1（下記）はポリシー(π(s))です。ポリシーは、状態sのとき最終報酬が最大になる行動(a)を選択します。
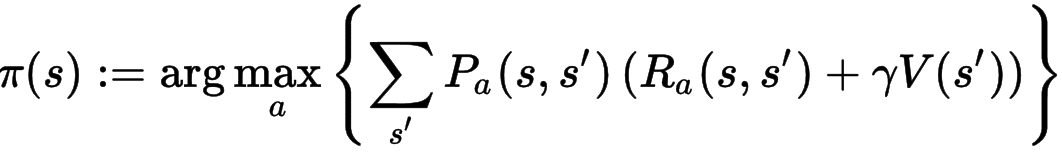policyーーーーー①
方程式2（下記）は報酬(V(s))です。上記の方程式1のポリシーに従って行動を選択したとき得られる報酬の期待値です（状態遷移確率が掛かっているのがわかります）。
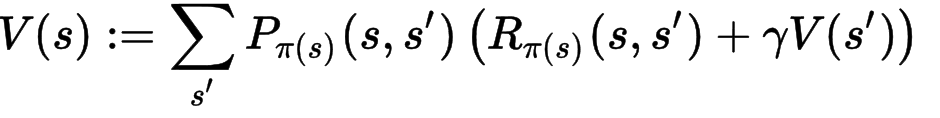valueーーーーー②
方程式１のポリシーを求めれば、MDPを解くことができます（要するに、このポリシーを従って行動すれば、最大報酬が得られる）。しかし方程式1にはV(s)が含まれているので、方程式2を解く必要があります。ところが方程式2を解くためには、方程式1のポリシーが分かる必要があります。つまり、両方程式を再帰的に解く必要があります。

MDPの解決手法は以下の二つに分かれます。

    （１）ポリシー反復法

Step 0： まずV(s)をRandomな数値に設定して、ポリシーを計算（方程式1）。
Step 1： 次にこのポリシーを固定し、V(s)が収束（値変更なし）するまで反復計算。
Step 2： このV(s)を利用して、ポリシー（方程式1）を再び計算する。
Step 3: Step 1とStep 2を繰り返す。

    （２）Value反復法

方程式1（π(s)）を方程式2に代入することで、下記のような一つの方程式になります（iは反復番号）。
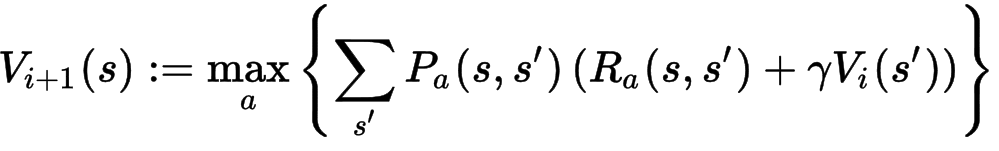
value-without
V_0(s)が分かればV_1を求めることができます。これを繰り返し、V_i(s)とV_i+1(s)の差は（ほぼ）なくなるまで反復計算します。ちなみに上記の方程式はBellman方程式と呼ばれています。

Deep Q-learning

強化学習モデルは原理的にはMDPの解決方法で求められるはずですが、伝統的なMDPがターゲットとしている小規模かつ有限状態空間ではない場合が多く更なる工夫が必要になり、おもに3つのアプローチがあります。（１）Q-Learning、（２）Temporal Difference Learning、（３）Direct Policy Search法：さらに、Policy Gradient法とPolicy Free法に分かれています。今回は、Q-learning法だけ紹介します。ちなみにGoogle AlphaGoは、Policy Gradient法を利用しました。（この手法なら、この論文又はこのブログを参考にしてください）。

Q-learningは、原理的には、上記MDPのValue反復法の改善版と見ることができます。まずQ関数をこのように定義します： Q：S × A → R。Q関数は、状態空間（S）と行動空間（A)から報酬への写像です。Q関数をDeep Neural Networkで表現する方法をDeep Q-learningを呼びます。

下記はDeep Mind社が発表したAtariゲームに応用したアルゴリズムの詳細です（元論文から引用）。
algorithm-pseducode
以下、いくつかの基本コンセプトと重要な部分を解説します：

    Episode


ゲームを例にすれば1試合に相当します。開始状態と終了状態が定義でき、ニューラルネットワークではEpochとも呼ばれます。
基本的には、終了状態まで報酬は分からないので途中状態の瞬時報酬が0ですが、報酬は終了状態から遡って割り引いた数値になっています（上記のPseudo-codeのy_jの2番目計算式）。終了状態なら、当然その時点の瞬時報酬が得られます（上記のPseudo-codeのy_jの1番目計算式）。

    Experience Replay


Experience Replay (経験再生)とは、一度経験した状態などの情報（transition）をメモリー保存し、次のニューラルネットワーク学習に再利用する手法です。保存情報はこのような4-tupleです（transitionとも呼ばれます）。
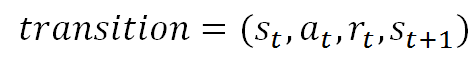
transition
つまり、t時刻の状態s、行動a、瞬時報酬r及び次のt+1時刻の状態からなるTupleです。過去経験を蓄積しそれをランダムに繰り返すことで、学習サンプルを増やすことができます。

    Q-network


Q-LearningはQ関数（Q(s,a)）を求めることです。Q関数をニューラルネットワークで表現したとき、これをQ-networkと呼びます。上記のPseudo-codeに示したように、y_jとQ_jの誤差（L2 Normal）をLoss Functionとして定義して、上記のExperience Replayに蓄積したSampleからランダム的にMiniBatchを作り、そのMiniBatchのサンプルからGradient Descent法でθを求めます。この学習プロセスは、普通のDeep Neural Networkと全く同じです。

    Explore & Exploit


Q-learningにおいて、もし過去の経験（データ）のみを開発(Exploit)すれば、当然未来の新しいEpisodeに対応できません。さらに学習過程途中で学んだPolicyを完全に信頼し、それに従って行動すると早期のGood Sample (高い報酬)に偏り、全局的な最適行動を探索(Explore)できなくなります。そこでExploreとExploitのバランスを取るため、ε-greedyという戦略を利用します。学習早期では、そもそも学んだPolicyの精度があまり良くないのでεの確率でランダムな行動を取り、学習後期にはPolicyをより信用してランダム行動の確率εを下げます。

RL4J

Reinforcement Learning4J （RL4j）はDeep Learning4j (DL4j)を利用して作った強化学習Frameworkで、つい最近リリースされました（DL4jと同じバージョン0.6.0）。Ruben Fiszel氏がSkymind社でインターンをした時に作ったもので、まだ未熟な部分もありますが様々な特徴もあるので検証してみました。

環境構築はソースからBuildするのは大変だが、リリースバージョンなら容易に構築できます。今回は簡単な例（Cart Pole）を実行してみました。下図（gif）のようにCart Poleを右か左に移動させて、なるべく長く立たせるというゲームです。このとき、状態空間が棒（Pole）の角度（水辺面基準）、行動空間が右移動と左移動（移動Speedが固定）、そして報酬は倒れるまでの経過時間です。
training_episode_batch
このゲームはOpen AI Gymのシミュレータをそのまま流用しています。OpenAI Gymは様々なゲームをシミュレートしているので、AIの研究には、特にモデル評価によく使われています。GymはPythonのライブラリですが、今回はRest APIサーバを経由してJavaで使っています。

下記のようなシンプルのソースで、上記のゲームを学習できます。ソースのコメントを読めば仕組みを理解できると思うので解説は省きます。ちなみに上記のAtariゲームでのDeep Reinforcement LearningはCNNを利用していましたが、今回のInput（状態空間）は画像ではなく数値のみなので、ニューラルネットワークは簡単なMLPを使いました。

public static QLearning.QLConfiguration CARTPOLE_QL =
new QLearning.QLConfiguration(
123, //Random seed
500, //Max step By epoch
300000, //Max step
150000, //Max size of experience replay
64, //size of batches
1000, //target update (hard)
50, //num step noop warmup
0.01, //reward scaling
0.99, //gamma
1.0, //td-error clipping
0.1f, //min epsilon
1000, //num step for eps greedy anneal
true //double DQN
);

public static DQNFactoryStdDense.Configuration CARTPOLE_NET =
new DQNFactoryStdDense.Configuration(
3, //number of layers
24, //number of hidden nodes
0.001, //learning rate
0.00 //l2 regularization
);

public static void main( String[] args )
{
//record the training data in rl4j-data in a new folder (save)
DataManager manager = new DataManager(true);

//define the mdp from gym (name, render)
GymEnv mdp = new GymEnv("CartPole-v1", true, true);

//define the training
QLearningDiscreteDense dql = new QLearningDiscreteDense(mdp, CARTPOLE_NET, CARTPOLE_QL, manager);

//train
dql.train();

//get the final policy
DQNPolicy pol = dql.getPolicy();

//serialize and save (serialization showcase, but not required)
pol.save("pol1");

//gym.upload(u'c:\\tmp\\gym-dqn') in python

//close the mdp (close http to Gym Server)
mdp.close();
}

Open AI Gymには、学習過程の可視化もサポートされています。上記の学習結果がLocalに保存されるので、GymのAPIを利用して自動的に学習情報がここにUploadされます。下図は上記ソースでの学習精度評価です。縦軸はScore（最終報酬）で横軸は学習回数（Episode数）です。学習回数が増えるほどモデルが徐々によくなり、最終的に収束している様子がわかります。
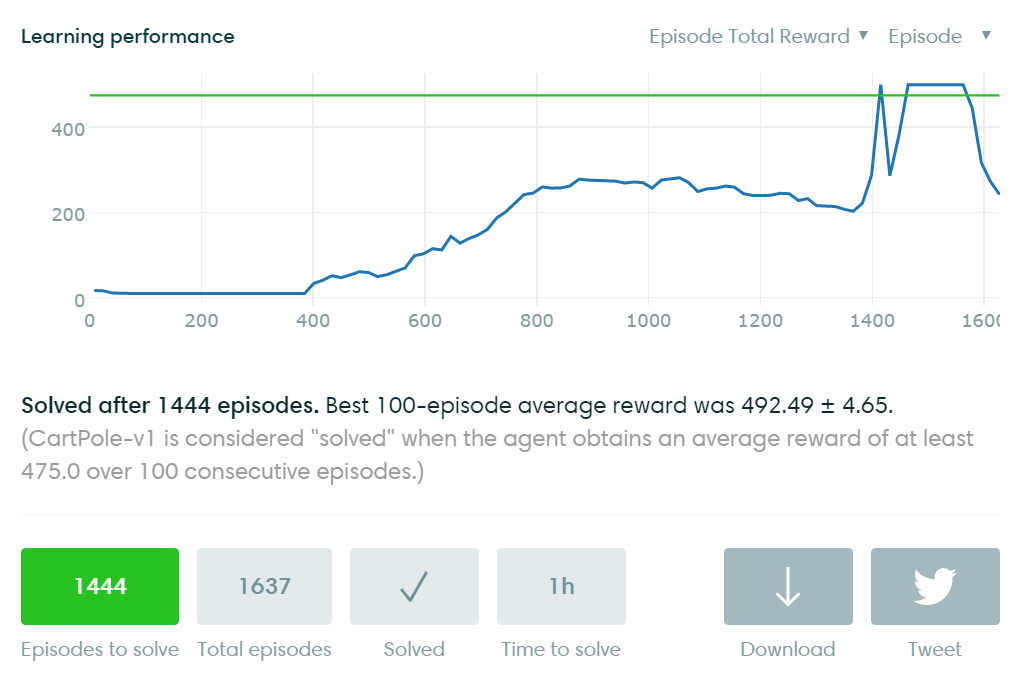
learning_performance

今回は強化学習の原理を説明しながら簡単な例を実行してみました。次回ブログでは、より広く深く検証する予定です。

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。

皆さんのご応募をお待ちしています。

  • Twitter
  • Facebook
  • はてなブックマークに追加

グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。

 
  • AI研究開発室
  • 大阪研究開発グループ

関連記事