2022.01.07

Python で映画をオススメしてみる
〜ユーザー評価に基づくレコメンド・システムの基礎とデータに潜むバイアス〜

目次
  1. 導入
  2. コンテンツ・ベース・フィルタリング
    1. MovieLens Dataset と映画ジャンルに基づく推奨
  4. 協調フィルタリング
    1. Feedback Matrix
    2. Matrix Factorization
    3. Matrix Factorization の実装
  6. 推奨システムのバイアスと対策
    1. ユーザー評価のバイアスとモデル性能
    2. 評価の観測構造とバイアスの補正
  7. まとめ
  8. 参考資料

導入

こんにちは次世代システム研究室の T. I. です。

さて、今回の Blog では、前回の Blog に引き続き「施策デザインのための機械学習入門」を参考に日常のデータサイエンスの業務で生じうるバイアスとその対処方法について紹介します。

今回の課題はレコメンド・システムです。我々がインターネットを利用していると、日常の様々な場面で商品・作品をお勧めされていると思います。これらは各種Webサービスが日夜集めたアイテムや顧客のデータを元になされています。アイテムの推奨には２種類考えられます。

(1) ユーザーが興味を持って何度も閲覧・視聴しているものを推奨して再度コンヴァージョン(購入・試聴)してもらう。

(2) ユーザーが興味を持ってもらえるであろう新しいアイテムを推奨して、購入・視聴をしてもらう。

この(1)については、ユーザーの過去の行動履歴があれば推定可能ですが、(2)の目的のためには、新しいアイテムの評価を推定が必要で(1)よりも難しい課題であります。直接には観測できないデータを推定するわけですから、適切な問題理解が不可欠です。

コンテンツ・ベース・フィルタリング

レコメンド・システムで使われる主な手法として

1. コンテンツ・ベース・フィルタリング
2. 協調フィルタリング

の２つが挙げられます。まず、前者のアプローチについて紹介します。

コンテンツ・ベース・フィルタリングでは、アイテム(コンテンツ)間の類似度を定義して、ユーザーの興味を持ったアイテムに近いものを推奨する手法です。

アイテムのもつ性質は特徴量ベクトルで表現すると、定量的にアイテム間の類似度を定義できます。下図はその概略図です。


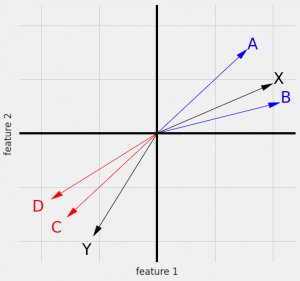
A, B が興味があるならば近いXを推奨し、一方で、C, D のアイテムに興味があるユーザーに対してはYを推奨すれば、そのユーザーの興味に近いアイテムを提示できます。

このようなアイテムの類似度のみでの推奨は、アイテムのどのような性質に着目するか？また、そのベクトルの類似度をどのように計算するかなどの考慮が必要です。

MovieLens Dataset と映画ジャンルに基づく推奨

では、簡単にコンテンツ・ベース・フィルタリングを実践してみます。
MovieLens dataset (https://grouplens.org/datasets/movielens/) では、映画のタイトル(公開年込み)とジャンルの情報がまとめられております。なお、ジャンルについては、１つの映画に対して１対１ではなくて、複数が記載されることもあります。

今回利用するデータは以下でダウンロードできます。
!wget https://files.grouplens.org/datasets/movielens/ml-1m.zip
!unzip ml-1m.zip
解凍すると映画、映画の評価、ユーザーの属性の３つのデータがありますが、まずは、movies.dat のデータを読み込んでみましょう。
import pandas as pd

df_movies = pd.read_csv('ml-1m/movies.dat', sep='::', engine='python', 
                        header=None, encoding='latin1',
                        names=['movie_id', 'title', 'genre'])
df_movies['year'] = df_movies.title.str.findall(r'\((\d{4})\)$').apply(lambda x: x[0]).astype(int)
# year の情報は後々の分析のために抽出
MovieLens 1M dataset では、1925-2000に公開された3883の映画が登録されており、


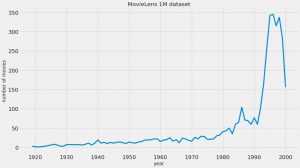
以下のように movie id, title, genre の column を持っています。(year の columnは前処理で追加したもの)


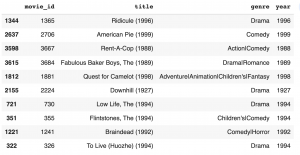
この映画のジャンルを元に類似するものを推奨してみます。
_df = df_movies.copy()
_df['genre'] = _df['genre'].str.split('|')
_df = (
    _df.explode('genre')
    .pivot_table(index='title', 
                 columns='genre', 
                 values='movie_id', 
                 aggfunc='count')
                 .fillna(0)
                 .astype(int)
)

genre_mat = np.array(_df)

norm = np.matrix(np.linalg.norm(genre_mat, axis=1))
similarity = np.array(
    np.dot(genre_mat, genre_mat.T)/np.dot(norm.T, norm)
)
df_sim = pd.DataFrame(similarity, index=_df.index, columns=_df.index)
ここでは一旦、処理のためにジャンルをone-hot vector の形式に変換してみます。


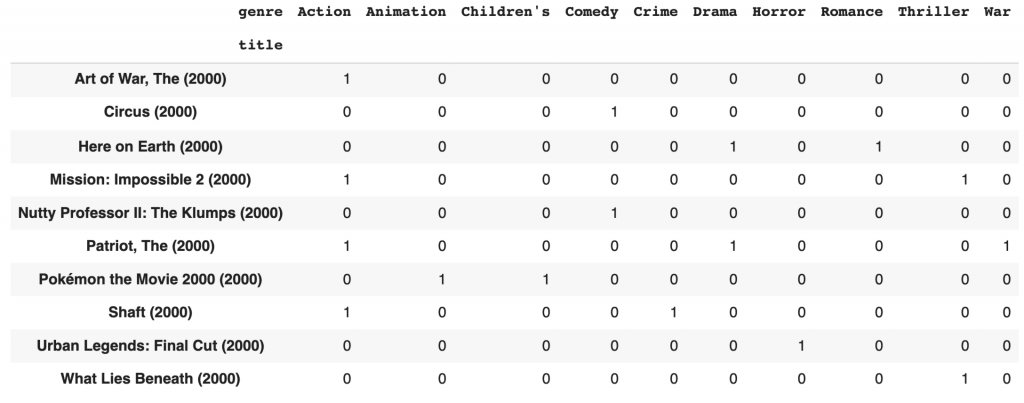
１つの映画に対して複数のジャンルが割り振られているので重複がありますが、登録されている件数は以下のようになっています。


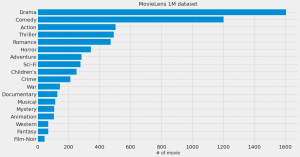
上記のコードで、映画間の類似度が以下のように集計できましたので、


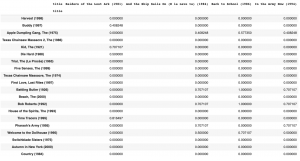
ある映画に対して、ジャンルが似た映画上位を試しに比べるとこんな感じになります。


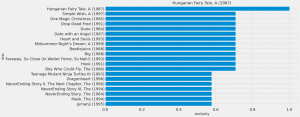
今回のようにジャンルの重複度だけでは、あまり候補を絞り込むことができないので、さらに映画の情報を追加しないと推奨システムとしては利用が難しそうです。

協調フィルタリング

コンテンツ・ベース・フィルタリングでは、アイテムの属性のみを利用していましたが、ユーザーの嗜好を含めた情報から推奨する手法を協調フィルタリングといいます。

Feedback Matrix

ここで個別のアイテムに対してユーザーの評価が得られているとします。

今回の MovieLens のデータセットの場合ですと、ユーザーと映画のIDとそれに対する
評価(１〜5の５段回)がこのように集計されています。データの取り込みは以下の通りです。
import datetime

df_rating = pd.read_csv('ml-1m/ratings.dat', sep='::', engine='python', header=None
                        ,names=['user_id', 'movie_id', 'rating', 'timestamp'])
df_rating['timestamp'] = df_rating['timestamp'].apply(datetime.datetime.fromtimestamp)

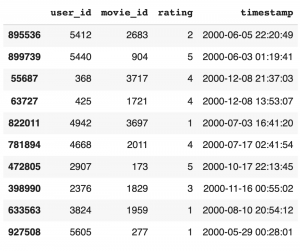
このような評価(Feedback)は、ユーザー数 x アイテム数の行列として表現できます。現実的には、ユーザーが全てのアイテムを評価していませんので、この行列のほとんどは空の行列となります。(下の表では未評価をゼロで埋めてあります)


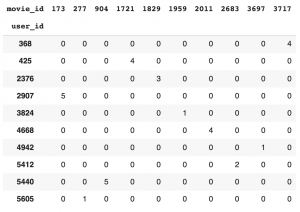
目的は、ユーザーの見評価アイテムに対して、期待される嗜好度合いを推定、そして高いものを推奨してコンバージョン(アイテムの購入や試聴)してもらうことです。

ここでの movie_id は、先程の movies.dat の movie_id と対応しますのでデータを結合すれば、無味乾燥な id ではなく具体的なタイトルと評価がわかり興味深いです。
df_ml = pd.merge(df_rating, 
                 df_movies[['movie_id', 'title', 'year']], 
                 on='movie_id', how='left')
さて、どんな映画のレビューが多いでしょうか？


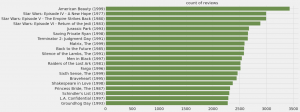
なるほど、という感じの錚々たる映画タイトルが並んでますね。では、これらの映画の評価はどうでしょうか？


さすが人気作品だけあって、高評価のレビューが多いですね。では、某シリーズの評価はどんなものでしょうか？


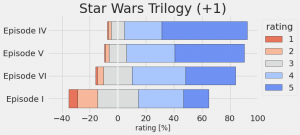
う〜ん、やはり、シリーズを重ねるごとに評価がだんだんと厳しくなっていきますね(II->III->VII->VIII->IX)。

さて、こうやって、EDA(Explanatory Data Analysis)で、遊ぶのはデータの把握には重要ですが、いつまでやっても解析が進みませんので、そろそろ本題に戻ります。

Matrix Factorization

Matrix Factorization は Feedback matrix で観測されていない評価を推定する手法です。観測されたFeedback をユーザー行列(P)とアイテム行列(Q)の積として近似します。

ここで、元の行列はユーザー数 m x アイテム数 n として、ユーザー行列(P)とアイテム行列(Q)は、それぞれ n x k と k x mの行列となります。ここで、k は特徴量を埋め込む次元数に対応したハイパーパラメータです。

Matrix Factorization の実際のイメージは以下のようになります。赤く塗ったマスは観測されていないユーザーの評価をユーザー行列とアイテム行列の積で推定します。(適当に作ったサンプルなのでちょっと変な数値も出ていますが)


 

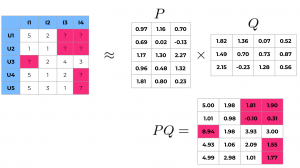
この計算は以下のような目的関数を定義し、最小化すればよいです。


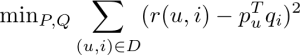
これは一般的に機械学習で利用されれる Stochastic Gradient Descent の手法を用いれば効率的に最小化できます。また、ユーザーやアイテムごとのバイアスの項を加えるなどの補正も考えられます。

Matrix Factorizationの実装

では、先ほど得られたサンプル・データを元に簡単に実装してみます。正則化項も加えた場合、


予測誤差 に対して以下のように順次更新することで計算できます。(αは学習率)

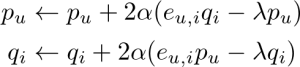
n_users = 5
n_items = 4

# initialize feedback matrix
R = np.array([[5, 2, 0, 0], [1, 1, 0, 0], [0, 2, 4, 3], [5, 1, 2, 0], [5, 3, 1, 0]])
ratings = []
for user in range(n_users):
    for item in range(n_items):
        if R[user,item] != 0:
            ratings.append([user, item, R[user,item]])

# R
# array([[5, 2, 0, 0],
#       [1, 1, 0, 0],
#       [0, 2, 4, 3],
#       [5, 1, 2, 0],
#       [5, 3, 1, 0]])

alpha = 0.0002
lambda_ = 0.02
k = 3
p_users = np.random.rand(n_users, k)
q_items = np.random.rand(n_items, k)
for iter in range(10000):
    for user, item, rating in ratings:
        _pred = p_users[user] @ q_items[item]
        err = rating - _pred
        p_users[user,:] += alpha * (2.0 * err * q_items[item,:] - lambda_ * p_users[user,:])
        q_items[item,:] += alpha * (2.0 * err * p_users[user,:] - lambda_ * q_items[item,:])

print(p_users @ q_items.T)
#  [[ 4.99679368  1.97846771  1.80619416  1.90240633]
#  [ 1.00532748  0.97694863 -0.09778591  0.30744267]
#  [ 8.94208881  1.97955001  3.93211154  3.00003764]
#  [ 4.93061087  1.06020728  2.09390243  1.54747828]
#  [ 4.98767916  2.97632775  1.0093586   1.77344618]]
このような簡単な実装ですが、Matrix Factorization によりユーザー行列とアイテム行列に分解できました。これを基に上の例で示したとおり、未知の映画に対するユーザー評価について推定できます。評価が高く予想される映画を推奨すれば、ユーザーの満足度も高くなると期待できます。

推奨システムのバイアスと対策

ユーザー評価のバイアスとモデル性能

上記の分析で未知のアイテムに対するユーザーの嗜好度合いの推定ができました。その目的関数としてユーザーの嗜好度合いと予測の乖離度を最小化しましたが、この点について注意が必要です。

実は、観測される確率にはユーザーの回答確率などに様々なバイアスが存在するため、単純に観測結果を基にモデルを作成すると、回答確率の高いものにバイアスのかかった学習をしてしまいます。そのような、バイアスのないレビューの評価の割合を正しく評価するためには「ランダムに抽出したユーザー」に「ランダムに選んだアイテム」を評価してもらう必要があります。

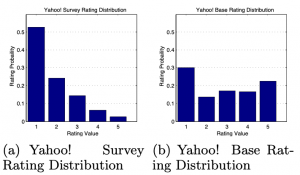
実際にこの種の実験を行ったサンプルデータについて分析した Marlin et al. ’07 によりますと、以下の左図のような分布となりました。右の図は、ユーザーが自身の興味に基づいたアイテムを評価した場合で、２つの分布は大きく異なります。これはユーザーはもともと興味のあるアイテムに対しては、高い評価を与えますが、そもそも好意を持たないアイテムは見向きもしない傾向があると言えます。


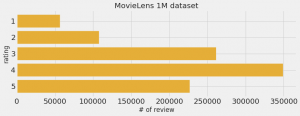
実際に MovieLens のデータセットの評価の分布は以下のようになっており、選択によるバイアスがありそうです。


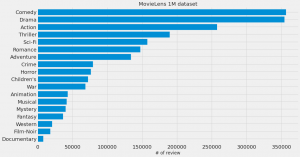
更に、評価の件数についても映画のジャンルによって偏りがありますし、その評価の分布もジャンルによって異なっています。(Crime とHorrorでは、評価の件数はほぼ同じですが、Horrowではのスコアが低い傾向があるのが興味深いでね、個人的な印象ではHorrowの方が当たり外れが大きいのでしょうか)



 

 

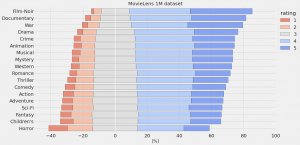
評価の観測構造とバイアスの補正

さて、上記のデータの観測構造をモデル化してバイアスを取り除きたいと思います。

naive な目的関数としては、観測されたデータ(D)に対して、損失関数()を最小化するような予測モデル のパラメータを探索します。


ここで、データの観測構造をモデルに組み込むために、あるユーザー・アイテムに対してそのレビューが観測される確率変数を以下で定義します。


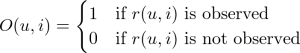
前回の Blog で紹介したようにデータの観測されやすさに差があるのでしたら、その分の重みつけをして目的関数を定義すれば良いのです。この確率変数の期待値を以下のようにし、


その重みつけの Inverse Propensity Score (IPS) 推定量を定義します。


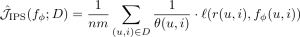
このIPS推定量を利用するためには観測されやすさの傾向スコア(θ(u,i)) を推定する必要があります。この書籍では、Yahoo! R3 dataset を用いた実験を紹介しており、今回のBlogでも利用する予定でしたが、(なぜか利用承諾が得られなかったため)引き続き MovieLens の dataset で実験します。

MovieLens dataset についても、アイテム選択バイアスに依存しない真の評価の分布がわかればよいのですが、今回の場合は Marlin et al. ’07 の結果を参考に rating の逆数に比例すると仮定してみます。

先ほどのコードを修正して実行してみます。また、このシンプルな実装では、データが多く処理に時間を要するため一部の映画に絞って実行します。
df_m = df_ml.query('year >= 1995').copy() # 1995年以降の映画に限る

user_id_map = {}
for i, id in enumerate(sorted(df_m['user_id'].unique())):
    user_id_map[id] = i

movie_id_map = {}
for i, id in enumerate(sorted(df_m['movie_id'].unique())):
    movie_id_map[id] = i

df_m['user_id_'] = df_m['user_id'].map(user_id_map).astype(int)
df_m['movie_id_'] = df_m['movie_id'].map(movie_id_map).astype(int)

alpha = 0.0002
lambda_ = 0.002
k = 10

df_m['inv_pscore'] = df_m['rating']

ratings = df_m[['user_id_', 'movie_id_', 'rating', 'inv_pscore']].values

n_users = np.unique(ratings[:,0]).shape[0]
n_items = np.unique(ratings[:,1]).shape[0]

p_users = np.random.rand(n_users, k)
q_items = np.random.rand(n_items, k)

for iter in range(100):
    for user, item, rating, inv_pscore in tqdm(ratings):
        _pred = p_users[user] @ q_items[item]
        err = rating - _pred
        p_users[user,:] += alpha * (2.0 * err * inv_pscore * q_items[item,:] - lambda_ * p_users[user,:])
        q_items[item,:] += alpha * (2.0 * err * inv_pscore * p_users[user,:] - lambda_ * q_items[item,:])

df_pred = pd.DataFrame(p_users @ q_items.T,
                       index=list(user_id_map.keys()),
                       columns=list(movie_id_map.keys()))
さて、Matrix factorization が完了しましたので、試しに映画を推奨してみます。
user_id = 5408
(
    df_m.query('user_id == @user_id')
    [['user_id', 'movie_id', 'rating', 'title', 'genre']]
    .sort_values('rating', ascending=False)
)
このユーザーのレビューの状況はこんな感じです。


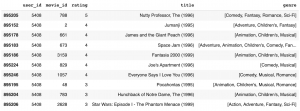
では、オススメの映画はどうなるでしょうか？Matrix factorization の結果は movie_id なので、映画の情報を結合してトップ20を見てみます。
_df = (
    df_pred.loc[user_id,:].sort_values(ascending=False).to_frame()
    .reset_index()
    .merge(df_movies, left_on='index', right_on='movie_id', how='left')
    [[user_id, 'movie_id', 'title', 'genre', 'year']]
)
_df.head(20)

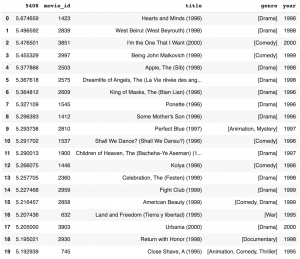
推奨結果がどのような評価を貰えるかは不明ではありますが、具体的に手を動かして実行してみるとレコメンド・システムの概略がよくわかりますね。

まとめ

今回のBlogでは、アイテムのレコメンド・システムの概略とユーザー評価で観測されるデータのバイアスと対処方法について紹介しました。
あくまでもExplicit feedback (明示的な評価) がある場合の分析でしたが、実際は、そのようなユーザーの評価が不十分な場合が多いため、より一般的な Implicit feedback (暗黙的な評価) をもとにした推奨アルゴリズムについても考える必要があります。その場合であっても、元となるデータがどのようなプロセスで取得されたか、どのような選択バイアスが残っているのかについて注意が必要です。

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。

参考資料

  • Twitter
  • Facebook
  • はてなブックマークに追加

グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。

 
  • AI研究開発室
  • 大阪研究開発グループ

関連記事