こんにちは。次世代システム研究室のK.N.（二人いるうちの一人）です。

 

僕はもともと確率系の研究室出身というのもあって、確率的なモデリングが好きなんですね。

データの条件付き確率を定義して、事前分布を決めて、事後分布を求めて。

MAP推定するもよし、変分Bayesの更新式導出して変分事後分布求めるもよし。

 

なんてやってたので、近頃の深層学習推しの流れを見ていて、「負けるなBayes！！」なんて思っているわけです。

 

とはいえもともと、単層全結合ニューラルネットワークは中間層のユニット数を無限大にすると、Gaussian Processと等価になることは古くに証明されていました。

ここで、多くの人が思うのは、「それなら、深層学習もなるのでは？」ということですね。

なるんです。

というわけで、その実装の一つである、NNGP（これで検索するとNearest Neighborも出てくる）が公開されていたので使ってみたよという記事です。

元になっている論文は、ICLR2018に採択されたDeep Neural Networks as Gaussian Processesです。

これ以降、ニューラルネットワークをNN、ディープニューラルネットワークをDNN、Gaussian ProcessをGPと表記します。

また、特に断らない限り、（ディープ）ニューラルネットワークは全結合で中間層のユニット数が無限大とします。

 

NNGP概要（ざっくり）

まず、（単層）NNがGPであるという話から。

NNは、入力の重み付き和に活性化関数を掛けて中間層とし、その中間層の重み付き和を出力層とする、というものです。

入力から中間層に向かう重みは独立なので、中間層はそれぞれ互いに独立になります。

独立なものに独立な重みをさらに掛けて和を取っているので、出力層は中心極限定理により、ガウス分布に従うことになります。この出力の確率分布はGPと等価で、その分散共分散行列は活性化関数と重みの分散から決まるカーネル関数になります。

無限の中間層の重み付き和を取るというところが、積分に相当しているとイメージすれば、GPの導出に詳しい人にはわかりやすいのではないでしょうか。

さて、このように単層ではGPであることは言えたので、深層も簡単ですね。

「互いに独立な素子が無限個ある層の重み付き和がGP」と言えたので、先ほどの単層NNで出力層に当たる素子を無限個並べてあげたら、「互いに独立な素子が無限個ある層」になるので、また次の層もGP、その次の層もGP…となるわけです。

 

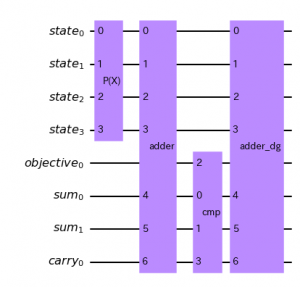
この論文と、その実装であるnngpでやっていることは、カーネルの更新です。

GPを定義することは、カーネル関数を定義することとほぼ等価なので、入力を元に一層目のGPカーネルを計算することができたら、そのカーネルを用いて次の層のカーネルを計算する…といったように更新を繰り返すことで、任意の深さの”DNNカーネル”を計算することができます。（もちろん、近似計算ですが）

 

実験

データセット準備

今回は、前回に引き続きKaggleに置いてあるFXのデータを加工して使います。

1分毎のドル円のプライスが4セットあるものになります。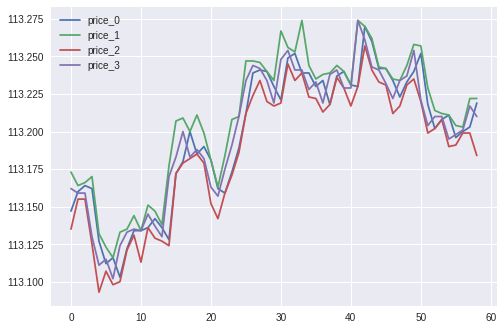

今回は、現在以前のプライスの挙動を使って、10分後のプライスの増減を推定しよう、というものです。

目的変数となる、「プライス増減」の定義をします。今回は、前回よりも少し実際の取引を意識したいと思います。

仮にプライスが当たったとしても、変動がスプレッドより小さいなら、儲けは出ないですね。ということで、「一つのプライスが10分後にスプレッド幅以上増える（減る）ことを、増減量+1(-1)」とします。4つすべてのプライスがスプレッド幅以上増えたら+4、全てが減ったら-4です。増えるプライスと減るプライスは互いに打ち消し合いますので、この値は、増える（減る）確信度のようなものです。

例えば、学習後の予測値が+4なら、全てのプライスが上がる、ということで、上がる目論見がかなり立つと捉えて、買いの選択をする、という感じですね。

この処理は、

1. 本来4つの目的変数を1つにまとめる
2. 単純な和などではなく、「増えた」「減った」「変わらない」の3値の和にすることで、1つのプライスの大きな変動といった影響を受けにくくする

という狙いです。こういう学習前後の処理は、データサイエンスっぽいですね。

4プライスの差分と、加工後の値がこちらになります。

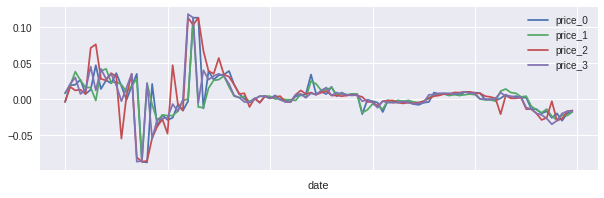
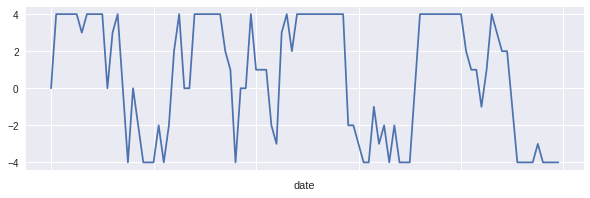
差分を取る時間間隔が10分もあると、なかなか変動も激しいですね。

回帰系は二乗誤差の影響で強いところに引っ張られる傾向があるので、そこら辺を抑えられている、という追加の効果も期待していいかもしれません。

 

さて、説明変数を作ります。

こちらは、現在のプライスと、それ以前のプライスを使って作ります。今回は、20分間のプライスを使いました。

GPに渡す入力なので、4プライス×20分の行列形式ですが、これは適当にベクトル化して渡しましょう。別に順番は関係ありません。（もちろん、サンプル毎に順番が変わるのはダメですが。）

さらに、簡単な加工をします。

いまはプライスそのものなので、百数十円の値ですが、これを0円付近に戻してあげましょう。

本来これは、biasに吸収される項ですが、biasの分散もパラメータの一つなので、これによってチューニングが若干手軽になります。

0円付近に戻す方法は、単純ですが、「現在のプライス4つのうち、1番目のもの」を引くとしましょう。

これにより、引き算に使ってあげた項目は当然0になるので、カラムから除外します。

すると、「4プライス×20分-1カラム = 79個」の説明変数ができました。

 

これで、

説明変数：79個の連続値

目的変数：[-4,+4]の9値を取る離散値

ができましたので、これを使って学習・予測を行ってみます。

 

評価基準

説明変数を使って、9値のいずれになるか予測する。この予測値を使って、どう評価するかというのも重要な項目です。

離散値なので、単純な的中率を使ってもいいですし、元の意味を考えれば連続値として考えて、二乗誤差などを使ってももちろんいいです。

しかし今回はFXです。お金を稼ぐためにやっています。（やっていませんが）

となると、普通はこの予測値に基づいて、売買をし、お金を儲ける、ということになります。

ということで、今回は、「予測値が-4または+4だったときのみ売買し、必ず10分後にそれを解決する」という戦略にします。売買を行う相手は、プライス1を出している相手とします。

勝敗は、売買から解決へのプライス１の変化量が、スプレッド幅以上であることと、変化方向の符号が予測値の符号と合致していること、両方が満たされていると勝ち、それ以外は負けです。

勝率が50%を超えたら儲けが出るということですね。

 

学習設定

学習は、

1. 少ないサンプル数を用いて二段階のグリッドサーチにより最適なハイパーパラメータを求める
2. 学習サンプルを増やし、最適なハイパーパラメータを用いて再度学習
3. 試験サンプルの予測を行い、評価する

の流れで行った。

全体で共通の設定は以下の通り

スプレッド幅：0.003

活性化関数：ReLu

DNNの深さ：８

DNNカーネルの積分計算に用いる分割数・幅など：デフォルト

 

1.ハイパーパラメータ学習

学習サンプル数：2000

検証サンプル数：1000

探索する重み・biasの分散（一回目）：[0.001 ~ 2.0]、[1.0 ~ 6.0]

探索する重み・biasの分散（二回目）：一回目のチューニング結果±0.5

評価基準：検証サンプル的中率

2.モデル学習

学習サンプル数：5000

試験サンプル数：2000

評価基準：先に述べたもの

 

結果

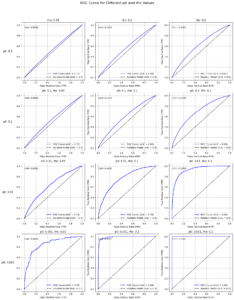
まず、決まった最適なハイパーパラメータは、重みの分散が1.0、biasの分散が2.5です。

このパラメータを用いて5000サンプルで学習し、予測と評価を行いました。

お待ちかねの結果です。

 

正答率47.9%

はい。今回のモデルでは、残念ながら儲けを得ることは難しいようです。

一応言い訳をしておくと、上がるか下がるかの2択を予測して、その通りだったかを当てるなら、ランダムでも50%当たります。ただ、今回はスプレッド幅以上の変動があるか予測しているので、それよりは難しいんですね。

 

まとめ・今後の展望

解析まとめ

今回取り上げたのは、全結合無限ユニット深層学習器と等価なGaussian Processを実現するためのカーネル関数を作ってくれる、NNGPという手法でした。

この手法を使って、前回と同じようにFXの値動きの学習モデルを立てました。

その際に、データの事前処理として、スプレッドに基づいた増減とその信頼度を定義し、学習時の予測対象としました。

今後の展望

1. より詳細なパラメータチューニング
2. 他の活性化関数
3. 検証サンプル的中率に代わる最適化基準

所感

今回もGoogle Colaboratoryを使って実験を行いましたが、リソースが足りないなという印象でした。

カーネル法を扱う上で必ず出てくるグラム行列が、サンプル数×サンプル数の行列になります。メモリももちろんですし、今回の手法においてはカーネルの計算が数値積分になるのでなかなか大変ですね。

一方で、深さ方向にはコストが線形のはずなので、少ないサンプルで深い階層をやりたい、という方には結構使いやすい手法かもしれません。

データの前処理や評価基準は、アイディアだけはいろいろと浮かびますが、何が最適か決めるのはなかなか難しいです。ただ、そういったアイディアを実際に試してみて知見を溜めることで、また新たなアイディアが浮かぶ、という試行と思考のループは大切だと思います。

FXという敵はやはり強大！ということでいまひとつな結果になりましたが、また、新たな手法と知見を持ち込んでトライしてみたいと思っています。

 

最後に

次世代システム研究室では、困難なデータに一緒に立ち向かっていけるデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。