時系列モデルの基本からFXをやってみる（二）

こんにちは。次世代システム研究室のC.Z.です。

前回のブログ（時系列モデルの基本からFXをやってみる（一） | GMOインターネットグループ 次世代システム研究室）は時系列モデルの基本からARMA系モデルについて復習と紹介しました。

GARCHモデルに関しては少し触れましたが、今回はGARCH系の詳細を紹介し、もっと全体的に時系列モデルを見たいと思います。

Volatility Clustering と GARCHの出場

ファイナンシャルのマーケットにおいて、よく見られる事実があります。それは、ある活発なマーケット時期の後でよくもう一つの活発なマーケット時期が続いている傾向があります。つまり、Volatilityがclusteringという性質を持っています。

Volatility clusteringを直観的に解釈してみると、マーケットがなぜ活発になるかと言いますと、大きいまたは予想できていないイベントかニュースが発生したためです。それに、このイベントの影響を完全に消化するため、必ず一定の時間がかかるはずです。統計的な言葉にすると、マーケットがtime-varyingな分散を持っています。

しかし、前回のブログにメインで紹介したARMA系モデル、上記のVolatility性質を無視し、マーケットの分散が不変と仮定していました。この欠点を解決するため、GARCHモデルの出番となります。

まずはGARCHの基礎モデルであるARCHから話します。ARCH(Autoregressive Conditional Heteroscedasticity)モデルのコンセプト自体は簡単で、MAモデルと近いイメージがあります。単語単位で分解すると、

• Autoregressive：自己回帰
• Conditional：条件付き
• Heteroscedasticity：違う分散

AutoregressiveとHeteroscedasticityはここまで紹介した通りですが、ConditionalはARMA系モデルには出てない単語です。

但し、実際はconditionalを含めこれらのコンセプトが全て共通しています。これを説明するため、もう少し時系列モデルの全体像から見てみます。

時系列モデルの全体像：ARMAからGARCH

マーケットデータX_tをt時刻のreturnとします。それに、この前に紹介したARMA(p,q)モデルは以下の式で表現できます。

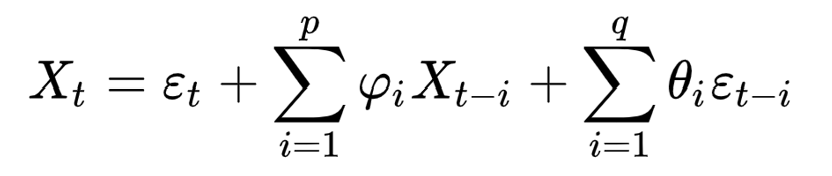
ここでは、残差epsilon_tがwhite noise ～W(0, sigma^2)となります。

この式をConditionalな形で書き換えると、以下のようになります。

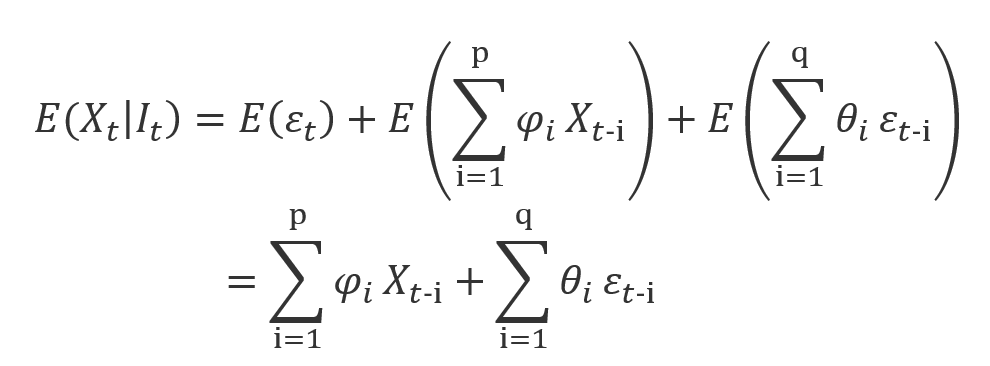
ここのI_tはt時刻に持っている情報であり、まさに過去のreturnであるX_t-iになります。

つまり、ARMAモデルはconditionalな平均値の計算プロセスを表現しています。

一方で、conditionalな分散の計算プロセスはまさにGARCH系モデルによる表現します。（モデルの詳細は後で紹介します）

ここのI_tはARMAモデルと同じ形で、theta_t-iが過去の情報になります。

まとめると、確率過程であるreturnに対して

• 条件付き平均値はARMAモデルよる表現できる
• 条件付き分散はGARCHモデルよる表現できる

ARCH(1)からスタート

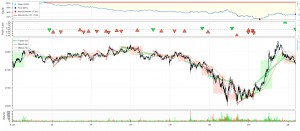
今回も同様にUSD/JPYを分析対象にしました。yahoo financeから5年分のdailyのプライスを抽出しました。

Yahoo Finance – Stock Market Live, Quotes, Business & Finance News

まず、USDJPYのreturnと一番シンプルのvolatility（squared return）を確認してみます。

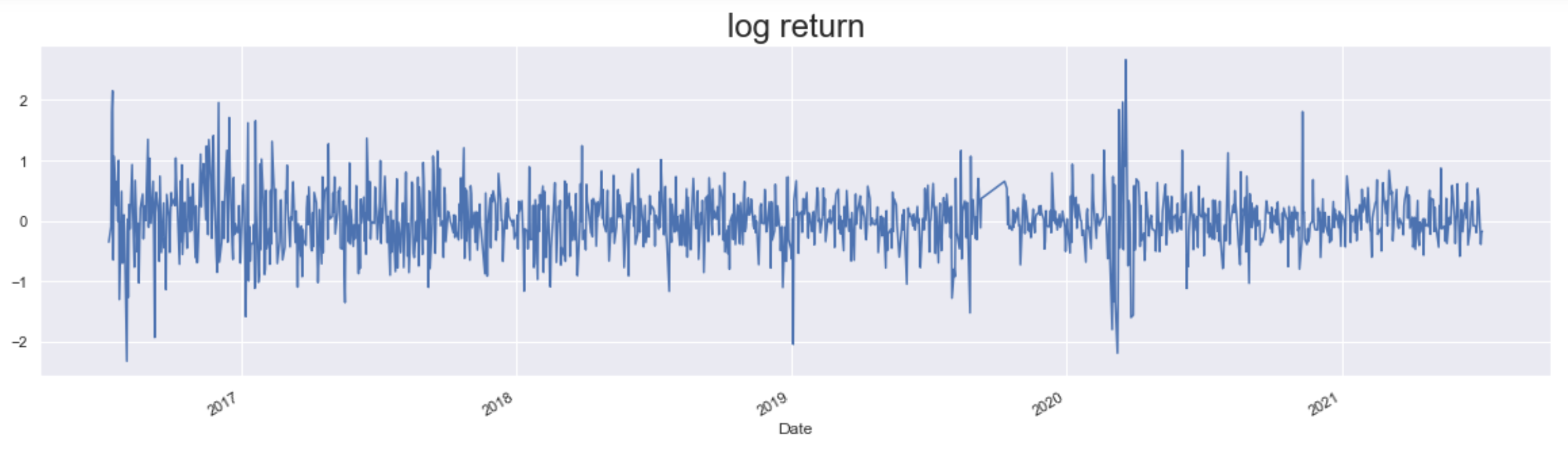
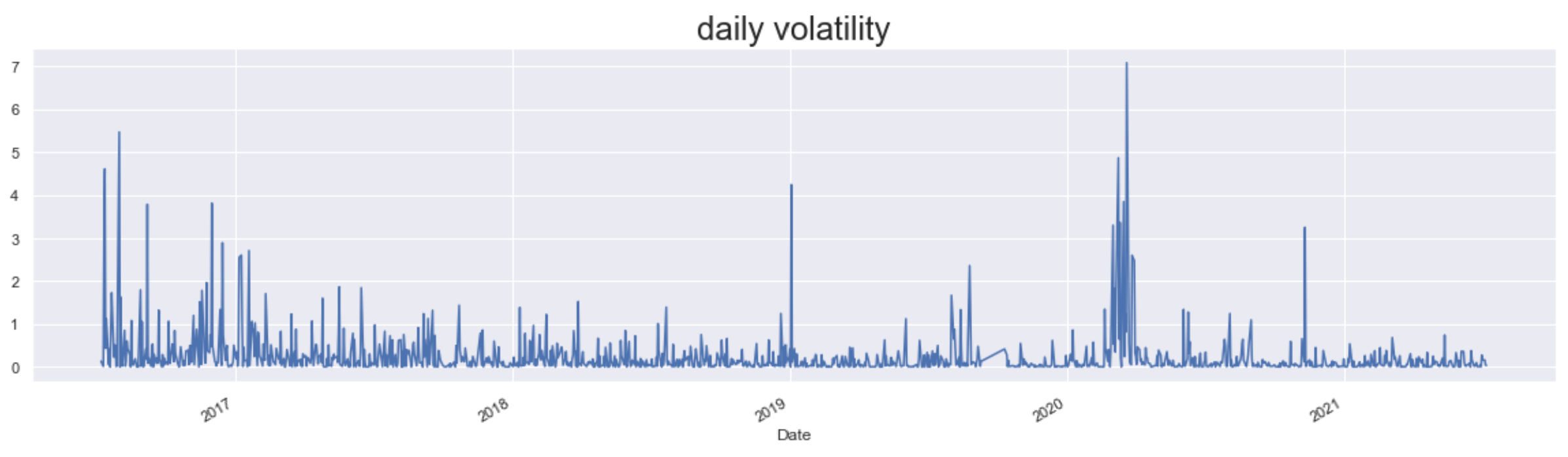
returnの変動が激しい時、やはりvolatilityも大きいですね。

次はそれぞれの自己相関も確認します。

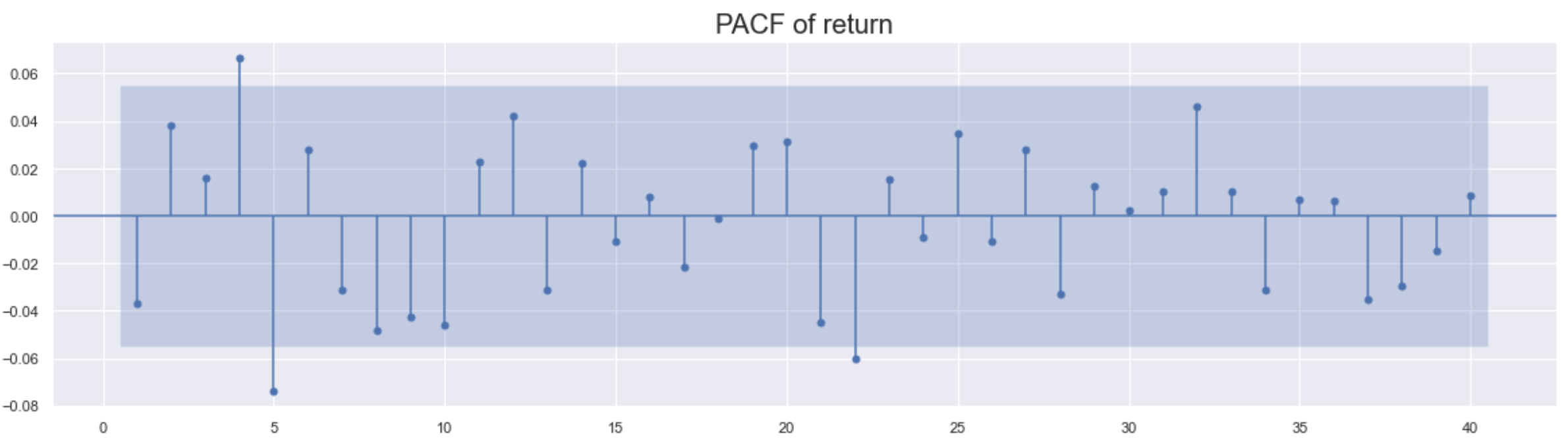
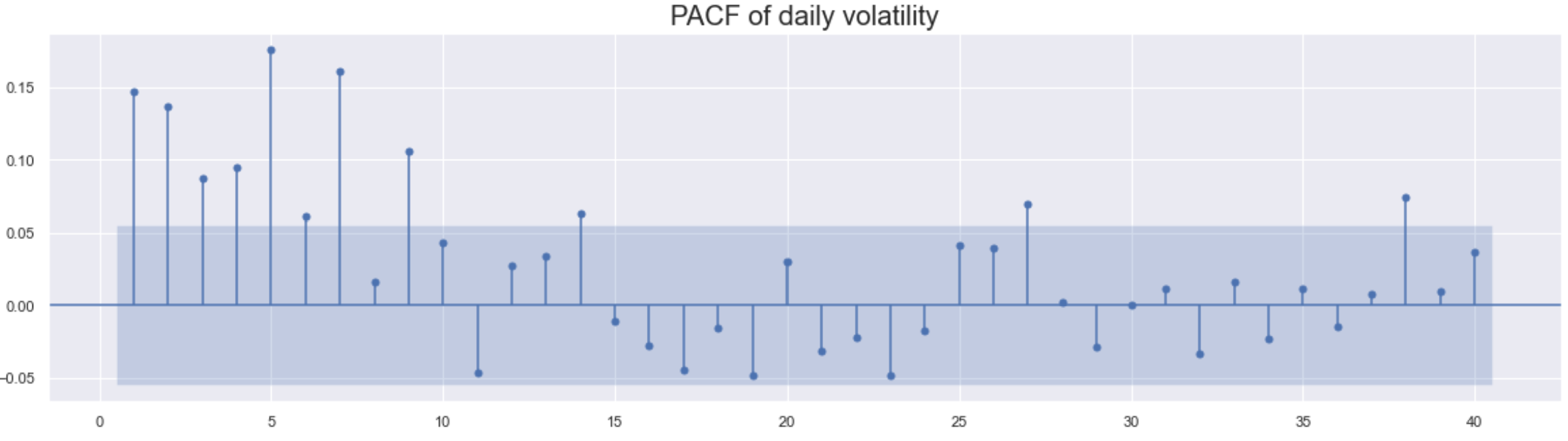
Volatilityのほうがlag 7くらいまでは有意な差が見られます。この結果より、ARMAの仮説である「volatilityがconstantでtime-varyingではない」が適切ではない可能性があることが判りました。

それではvolatilityをモデリングしましょう。以前の内容を少し復唱しますと、Returnは時系列であり、一定の確率過程を従います。Second-orderまで求めるので、確率過程の期待値と分散よりこのreturnのプロセスが判ります。つもり、下記のような式が書けます。

ここでは、裏で三つのモデルが存在します。

• 平均値プロセスモデル　→　μ

⇔ 0、常数、ARMAモデルなど

• 残差の分布　→　epsilon_t = sigma_t * W(0,1)

⇔ 正規分布、T分布など

• 分散プロセスモデル　→　sigma_t

⇔ 常数、GARCHモデルなど

まずは一番シンプルARCH(1)モデルからはじめます。X_tはARCH(1)過程だけに従います。

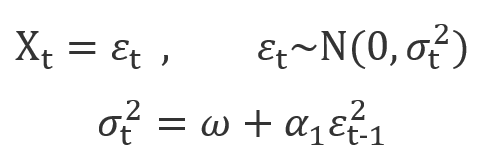
USD/JPYのreturnをARCH(1)にfitしましょう。

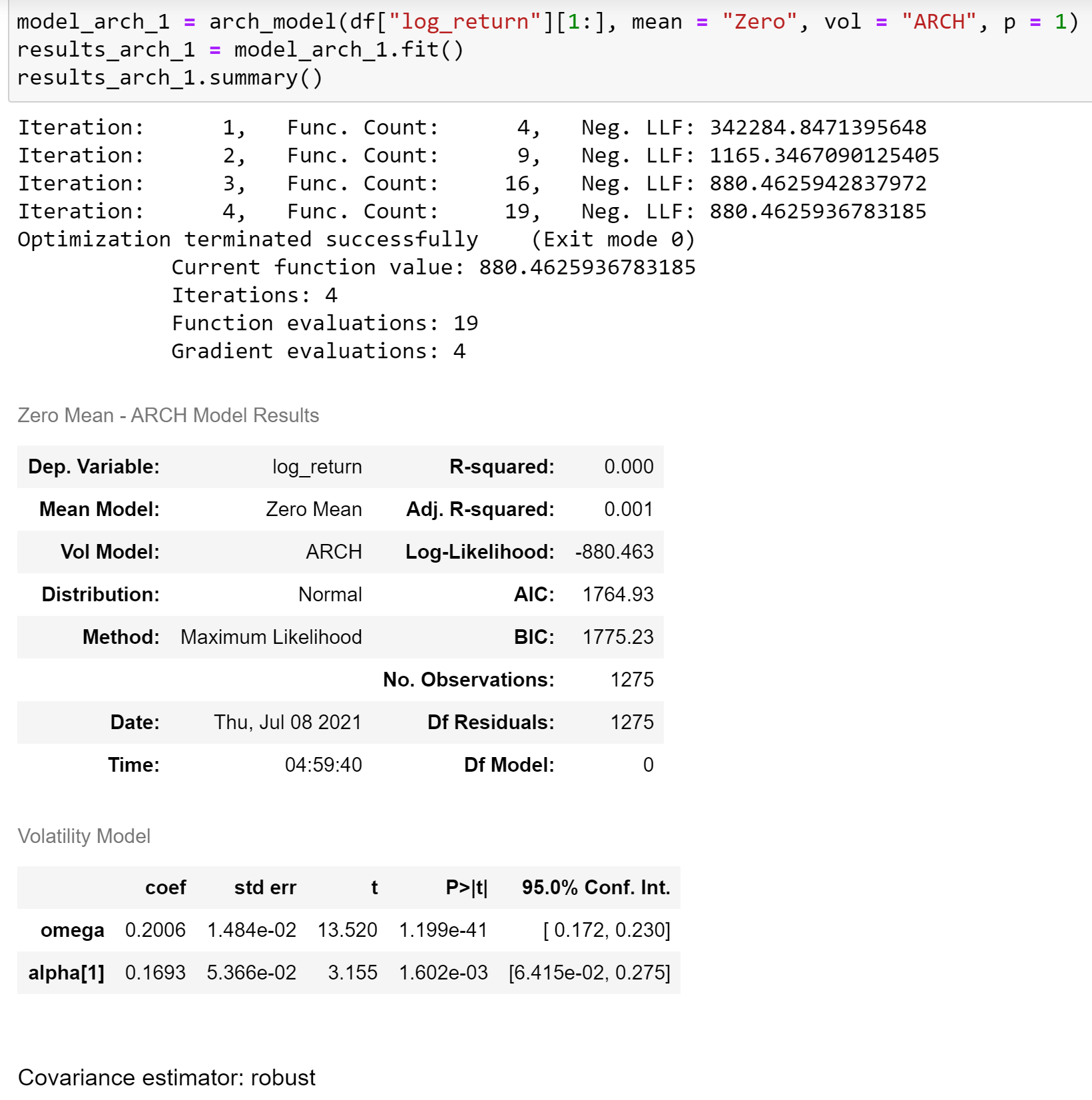
summaryテーブルからでも分かるように、ARCHモデルが想定した三つのモデルがあります。

• Mean Model: Zero Mean
• Vol Model: ARCH
• Distribution: Normal

結果を確認すると、Vol Modelの二つ係数とも有意であることが判りました。

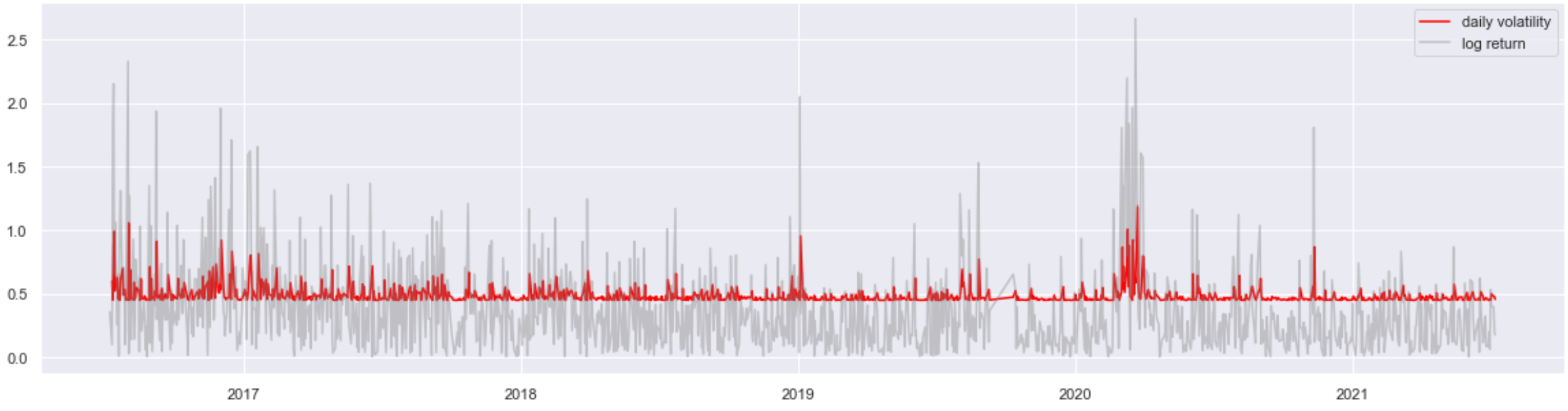
推定volatilityがある程度fitしたように見えました。

なお、一点補足します。モデルの性能評価上によく使われるR-squaredがここでは0となりますが、そもそも平均値に対するバイアス指標なので、分散の評価には適切な指標ではありません。

Clusteringのモデリング：GARCH

式から分かると思いますが、ARMAモデルに類比すると、ARCHモデルはMAの部分だけがあります。さらにARMAの思想を借りて、ARCHモデルを拡張することも可能です。つもり、一つbaselineのような過去の値を追加することで、モデル精度を上げることが期待されています。

直観的話に戻ると、「高いボラ→高いボラ、低いボラ→ボラ」というclustering傾向はAR項目追加より、モデル上で実現することが可能になります。

このARMA形のARCHモデルはGARCH（Generalized ARCH）モデルになります。

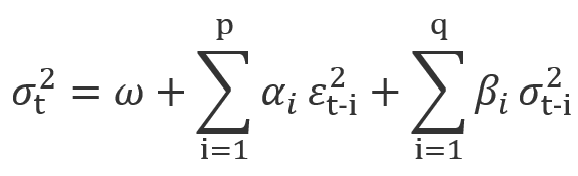
先と同じデータをGARCH(1,1)に投入してみると、

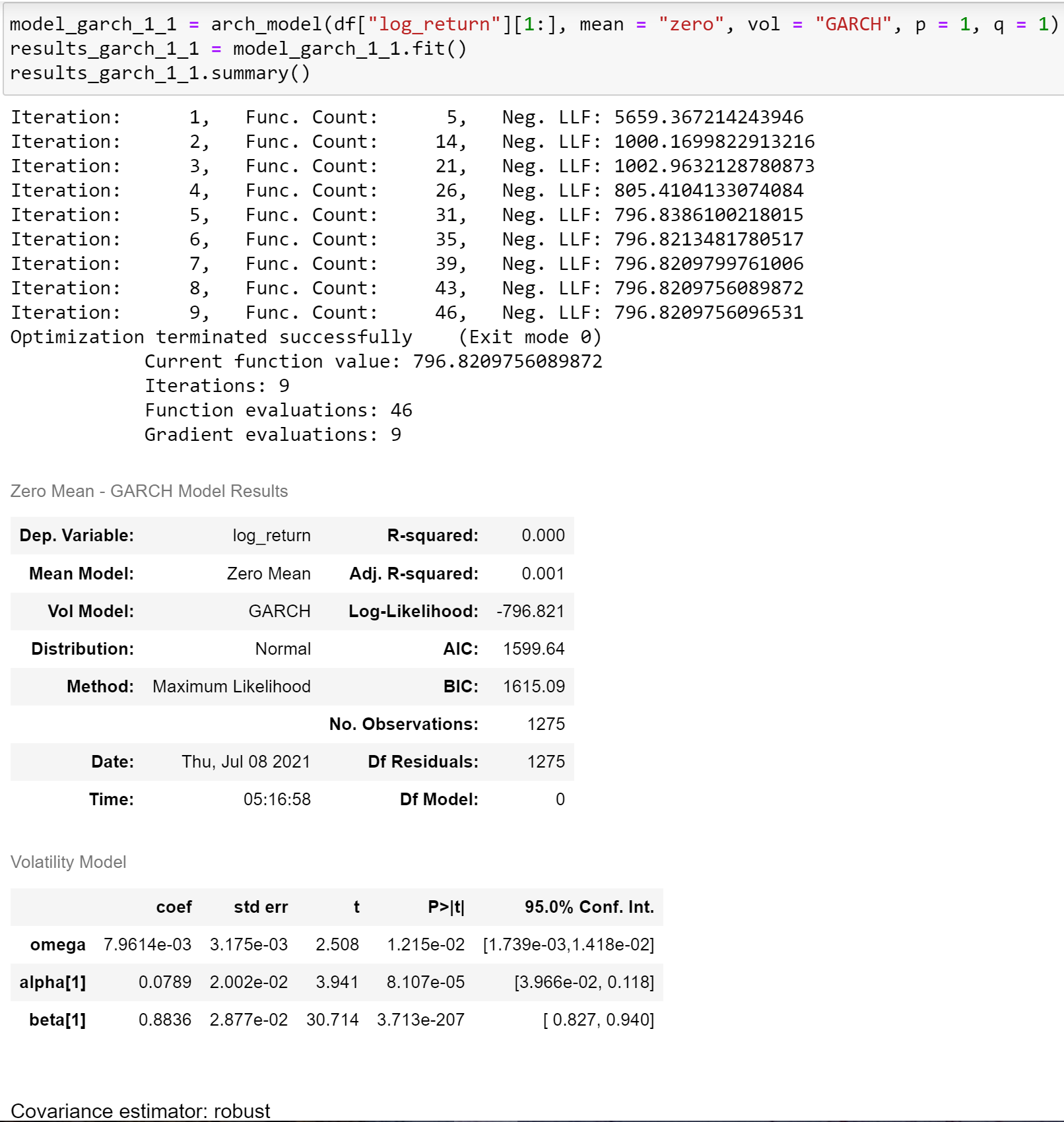
Log-LikelihoodでもAIC・BICでもGARCH(1,1)の優位性が見られました。なお、先と同様にvolatilityとreturnの関係図を確認します。

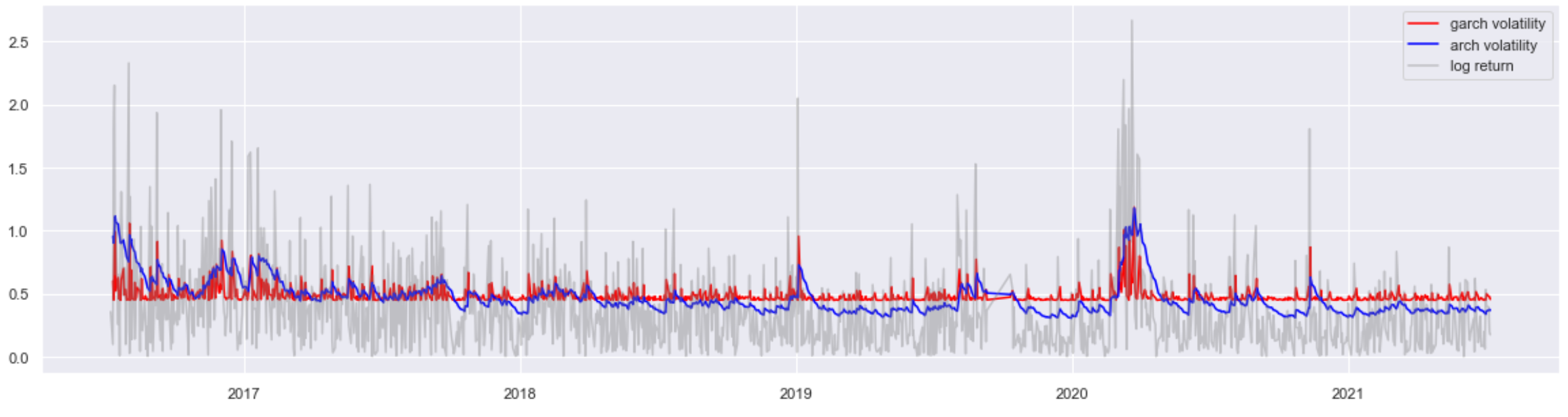
やはり、ARCH(1)よりデータをもっとfitしたように見えました。

詳細の数学推論を略しますが、金融分野のマーケットreturnといえば、GARCH(1,1)は常に最適なorderと考えられ、もっともよく使われているGARCH系orderとなります。つまり、(1,1)より高いorderを試す必要があまりないということです。

前回のblogで可視化したGARCH系モデルの選択にもあり、AIC・BICの基準なら確かにorder (1,1)が一番いい結果が得られました。

ここのEGARCHがGARCH系の中でもっともよく使われているモデルと言えるかもしれません。EGARCHの一番の特徴・メリットとしては、volatilityをモデリングではなく、volatilityのlogをモデリングします。そのおかげで、推定パラメータを制限かける必要がなくなります。

その一方、GARCHならvolatility自体が目的変数で、且つvolatilityがpositiveになる必要があるので、推定パラメータも必ず０より大きいという制限をつけないといけないということになっていました。

なお、上記model selectionに試した拡張モデルについて、rパッケージrugarchのドキュメントでまとめたように、データの性質によりそれぞれの目的に適します。

rugarch.pdf (r-project.org)

例えば、

• JGR GARCH：asymmetryのデータ
• FGARCH：非定常過程のデータ
• GJR GARCH：t分布と相性がよい
• など

があります。

平均値と分散の同時モデリング

上記のbest modelに、GARCH(1,1)モデルだけではなく、ARMA(1,0)も出できたと思います。

この前のセッションの内容を繰り返すと、

• 条件付き平均値はARMAモデルよる表現できる
• 条件付き分散はGARCHモデルよる表現できる

確率過程X_tに対して

残差のモデリングと同時に、μをモデリングすることも無論可能です。

この前でも例を挙げたように、0、常数、EMAなどの比較的にnaïveな統計モデルを使うことはもちろん、もっと高度的なARMA系モデルより表現することも問題ありません。

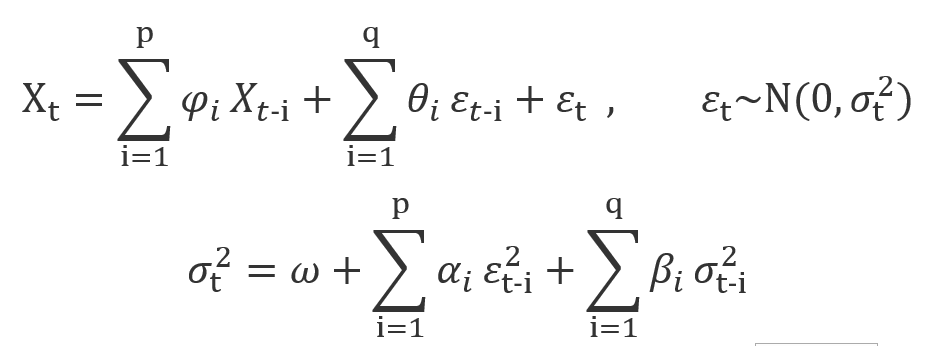
それでは、先のARMA(1,0) + GARCH(1,1)のbest model一回fitしてみます。

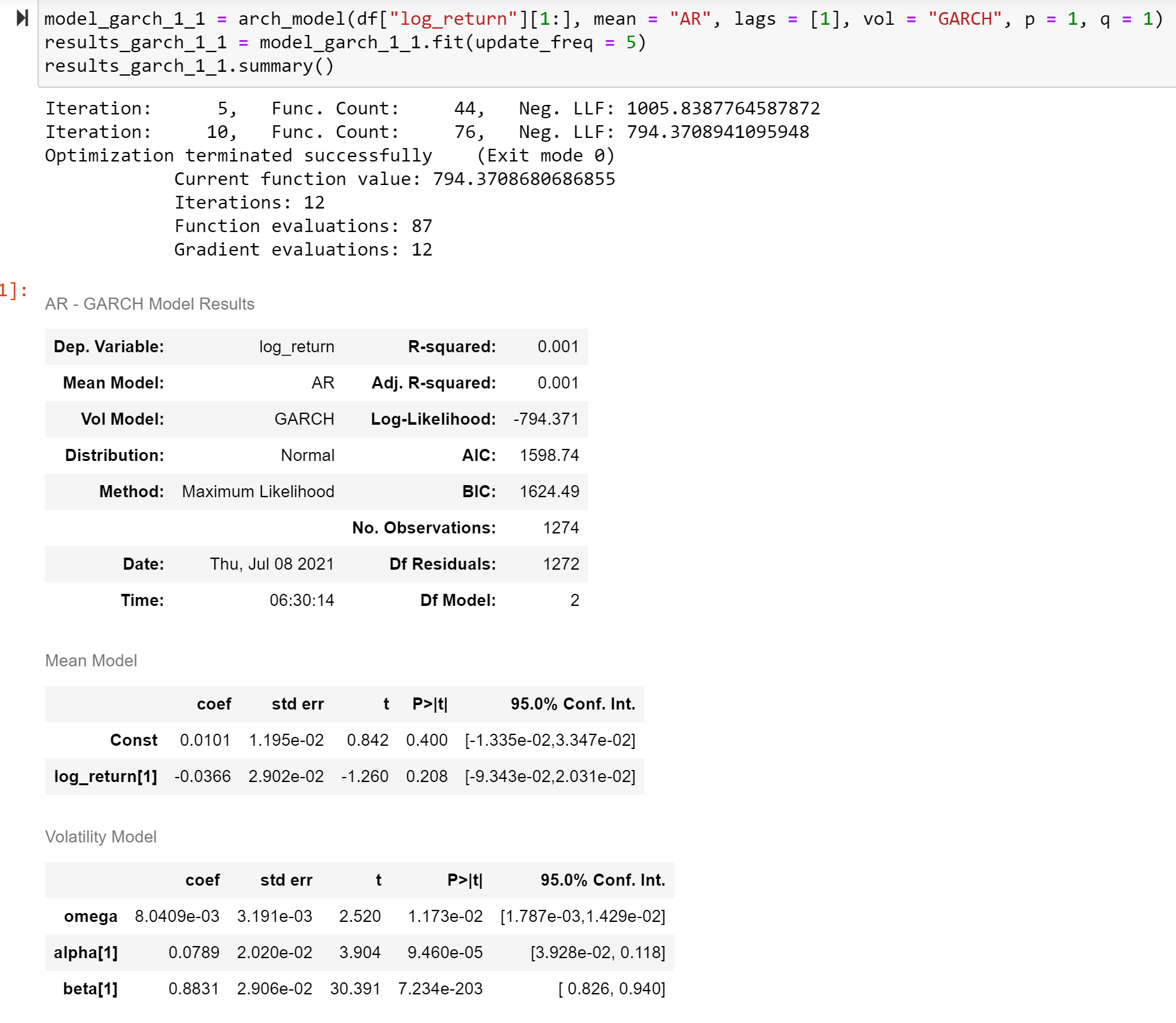
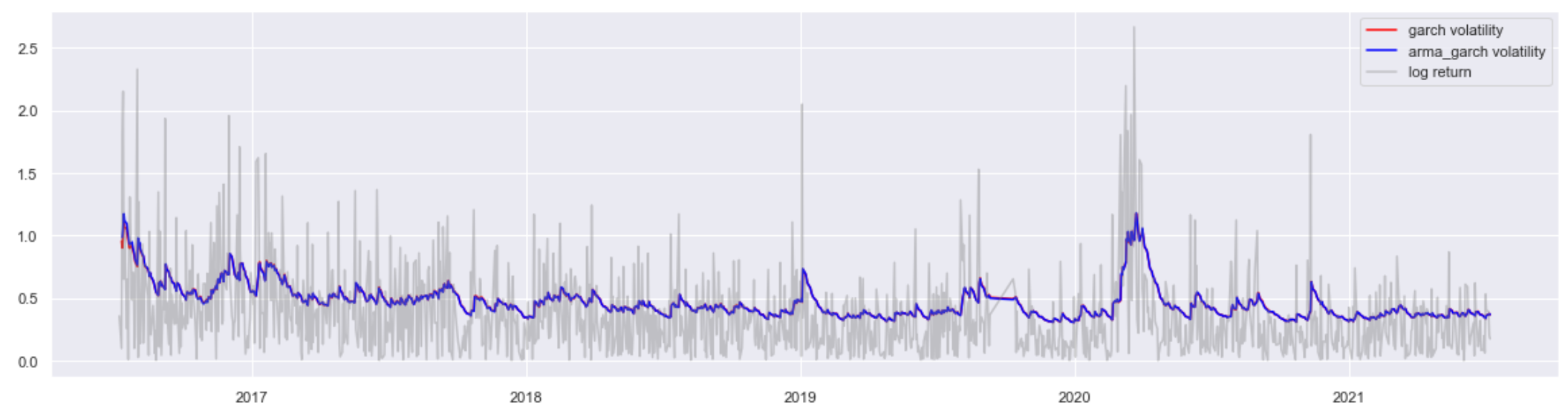
単純なGARCHより少しよい性能（LLが大きい、AIC・BICが小さい）が見られますが、ほぼ変わらないと考えてもよいです。

主な理由としては、mean modelの2つパラメータとも有意ではありません。つまり、ARMAモデルがデータの平均がうまく解釈できてない可能性が非常に高いということです。

最後に

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。