こんにちは。次世代システム研究室のC.Z.です。

最近の解析業務は時系列モデルがよく使われていました。この分野について自身の理解をさらに深めたく、実務でもっと円滑に運用できるように、時系列モデルの基本から復習しました。

今回のブログは時系列モデルの基礎コンセプトと統計モデルの紹介となります。

時系列モデルの基本

「時間とともに一定の確率性質でデータが形成される」は確率過程と定義できます。

株やFXのように時間につれ変化しつつあるものが、勿論上記の定義に満たします。では、分析対象の時系列データがどのような確率過程かを解かる必要があります。

時系列データの確率過程は定常過程と非定常過程があります。

時系列データの定常過程

ここの定常過程は、weakなsecond-order定常過程ではあり、

↓

strictな定常過程ではありません。

↓

• 結合分布は時間につれ全てのmomentは定常で変わりません。
  • 例えばthird-orderの歪度とfourth-orderの尖度も定常

非定常過程定は予測できない

上記定義した定常過程以外の確率過程は全て非定常過程です。

直観でもわかるように、時間に応じ分布が変化し、長期間でも収束できないなら、予測ができなくモデリングができないです。

というわけで、数多くロジックが定常過程を仮定したうえで行います。非定常過程→定常過程の変換もよく行います。

例えば、下記のようにrandom walk（非定常過程）からwhite noiseへの変換が簡単にできます。

residual error と white noise

時系列モデルの良し悪しを判断する場合、residual error（残差）がwhite noiseかどうかが重要な証拠です。

なぜかというと、residual errorは実際値とモデル予測値の誤差であり、もしある時系列モデルが時系列データの自己相関性質をうまく解釈できたら、residual errorが時間無相関のはずです。

white noiseの定義を見てみると、

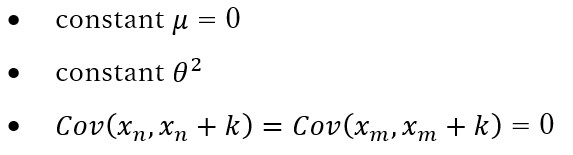
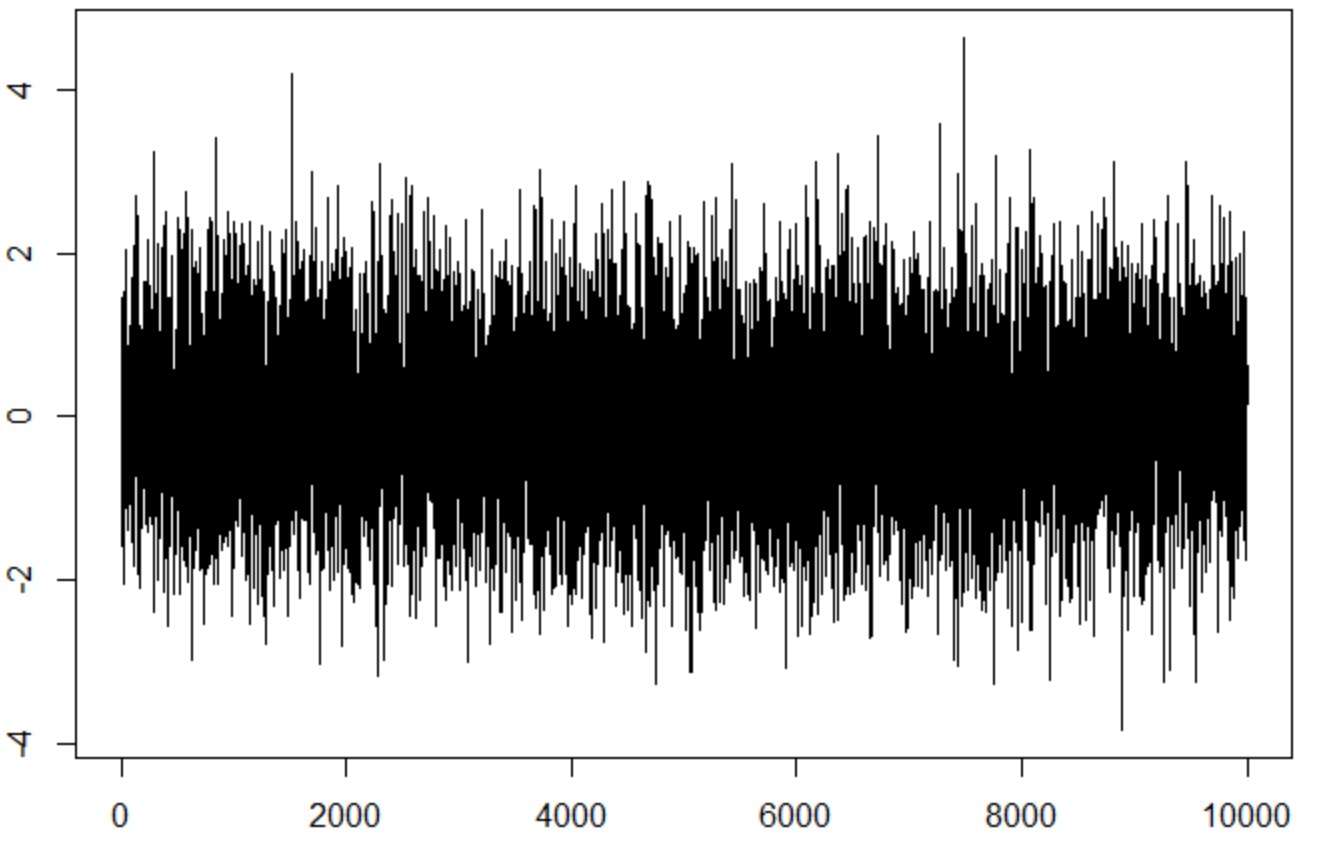
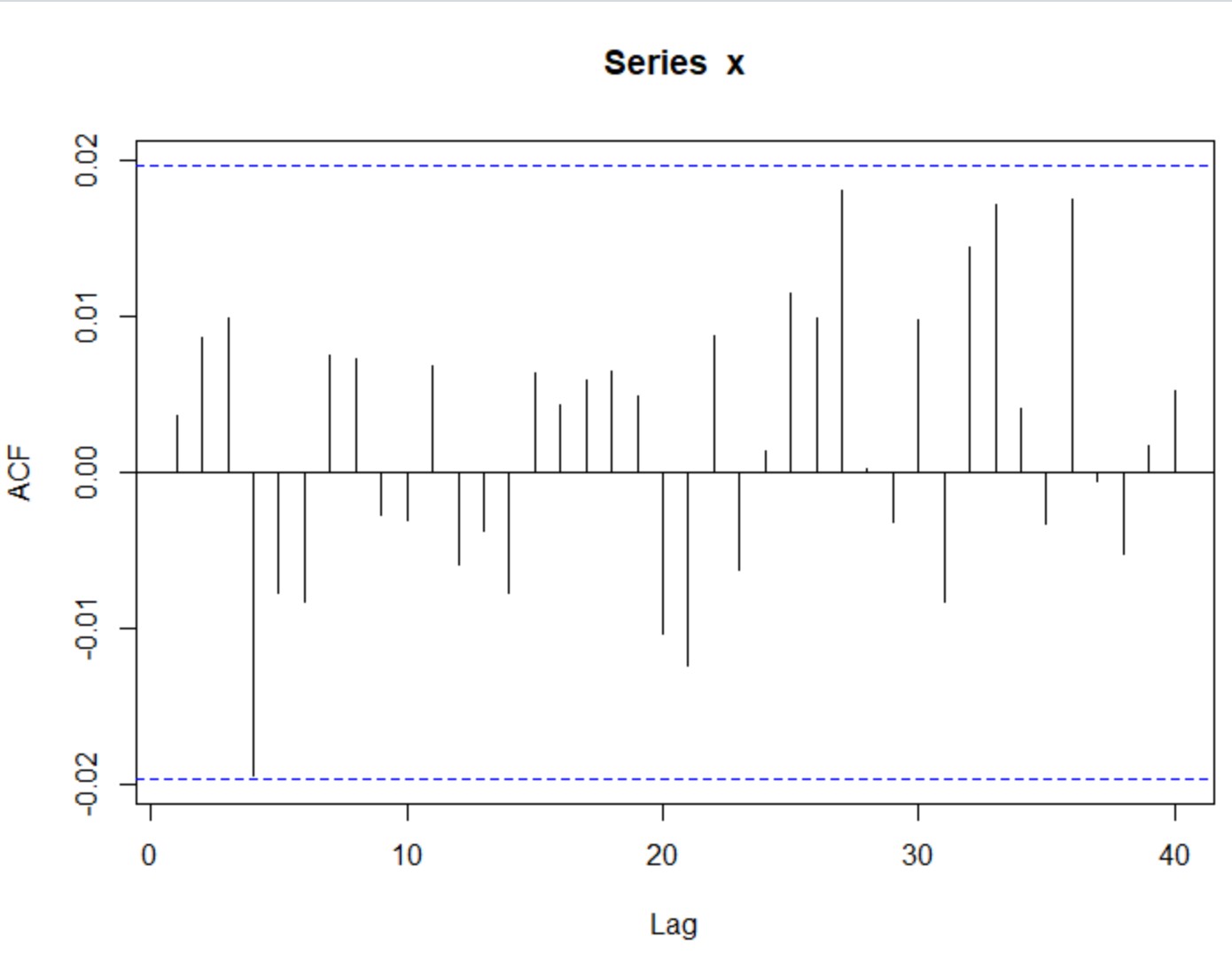
正規分布からランダムでデータを作成すると、white noiseが自己相関がないことが判ります。

x = rnorm(10000, mean = 0)
plot(x, type="l")
plot(acf(x,plot=F)[1:40])

random walkから連続な確率微分方程式

一番pureなrandom walkはシンプルで、ただ以下のように過去のデータ+white noiseになります。

w = rnorm(10000, mean = 0)
x = rep(0, 10000)
for(t in 2:10000) 
  x[t] = x[t-1] + w[t]
plot(x, type="l")
plot(acf(x,plot=F)[1:40])

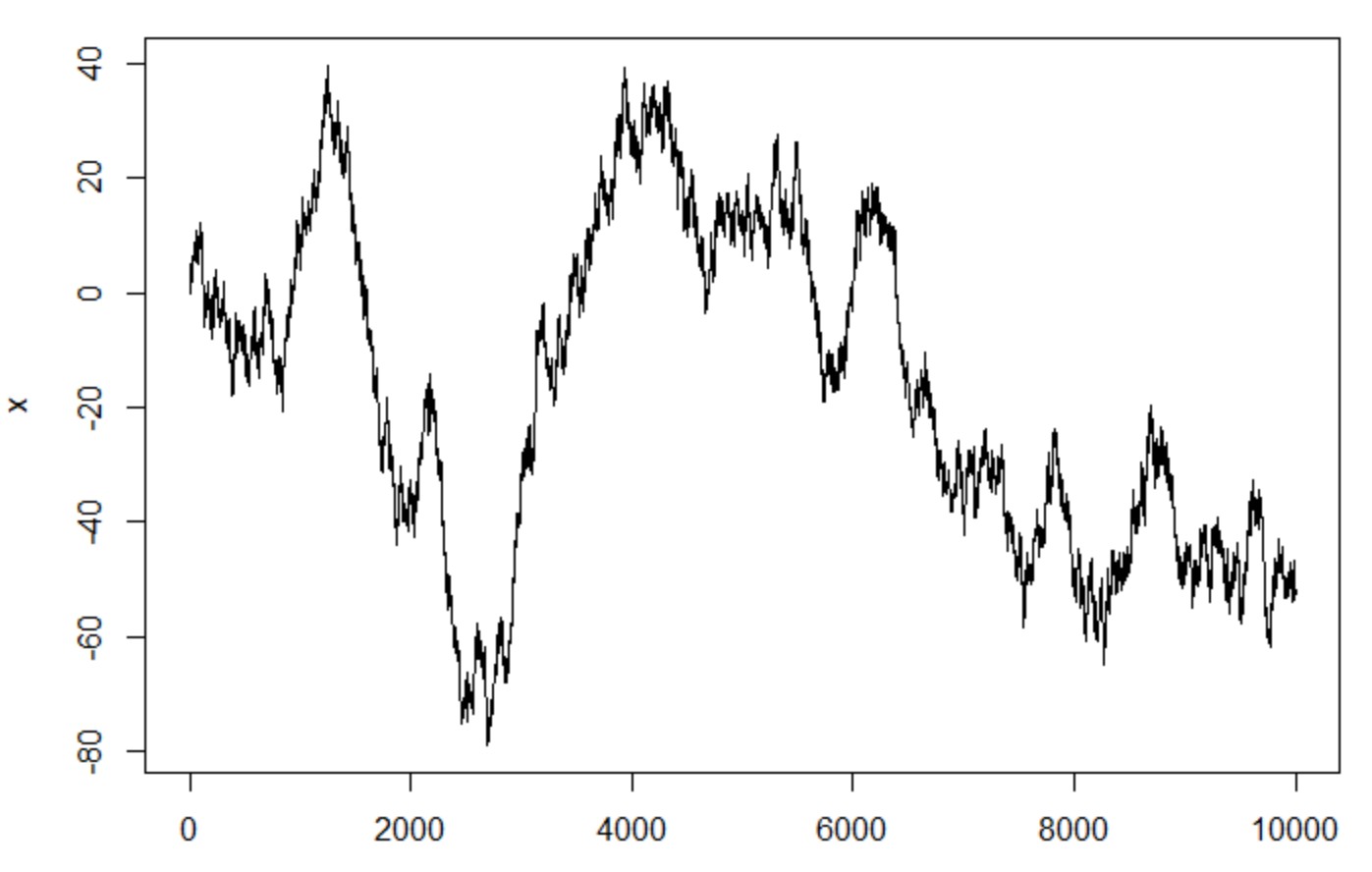
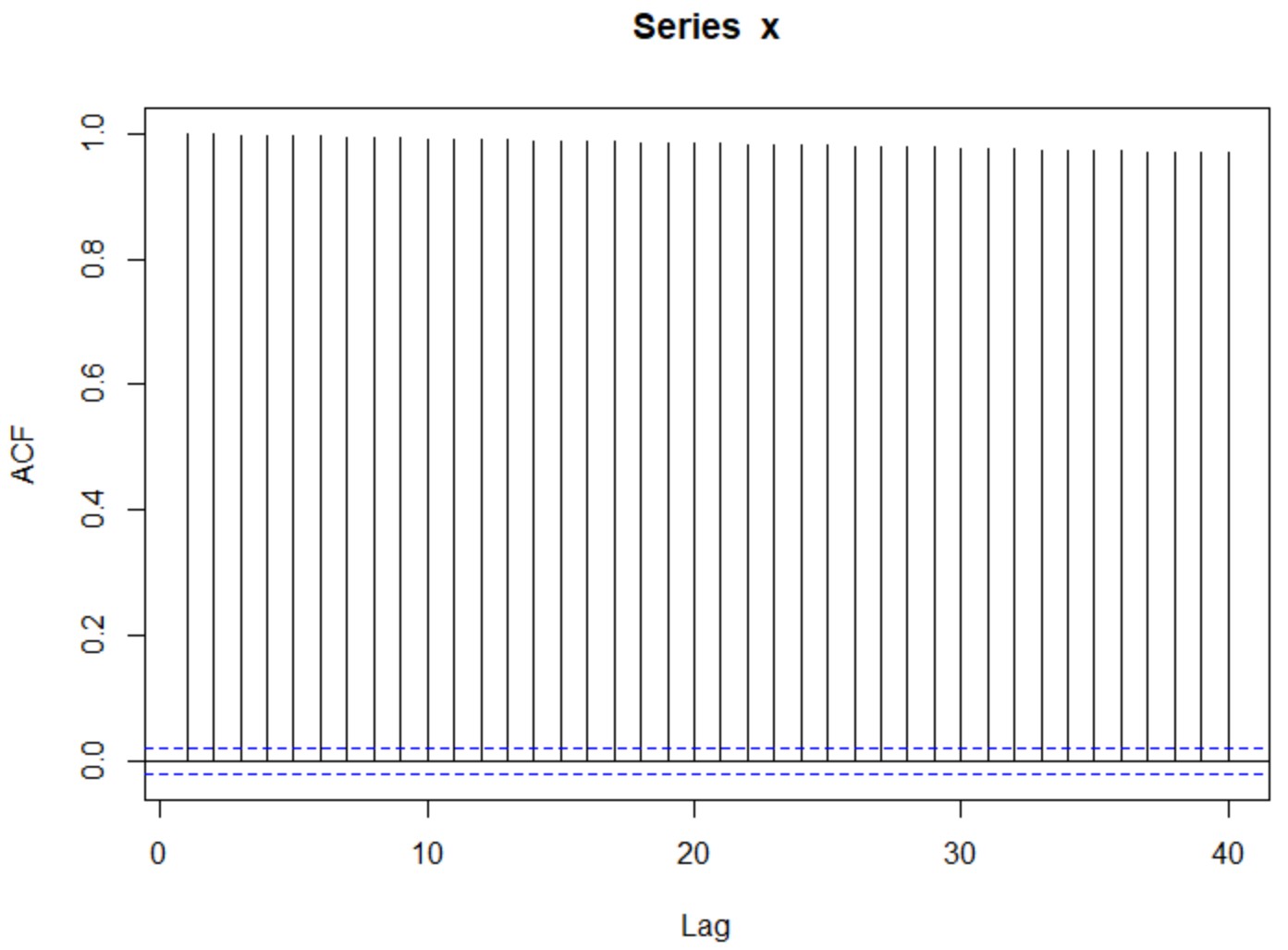
予想通り、自己相関が見えました（PACF使うと、lag_1だけが有意差があります）

plot(pacf(diff(x, na.action=na.omit),plot=F)[1:40])

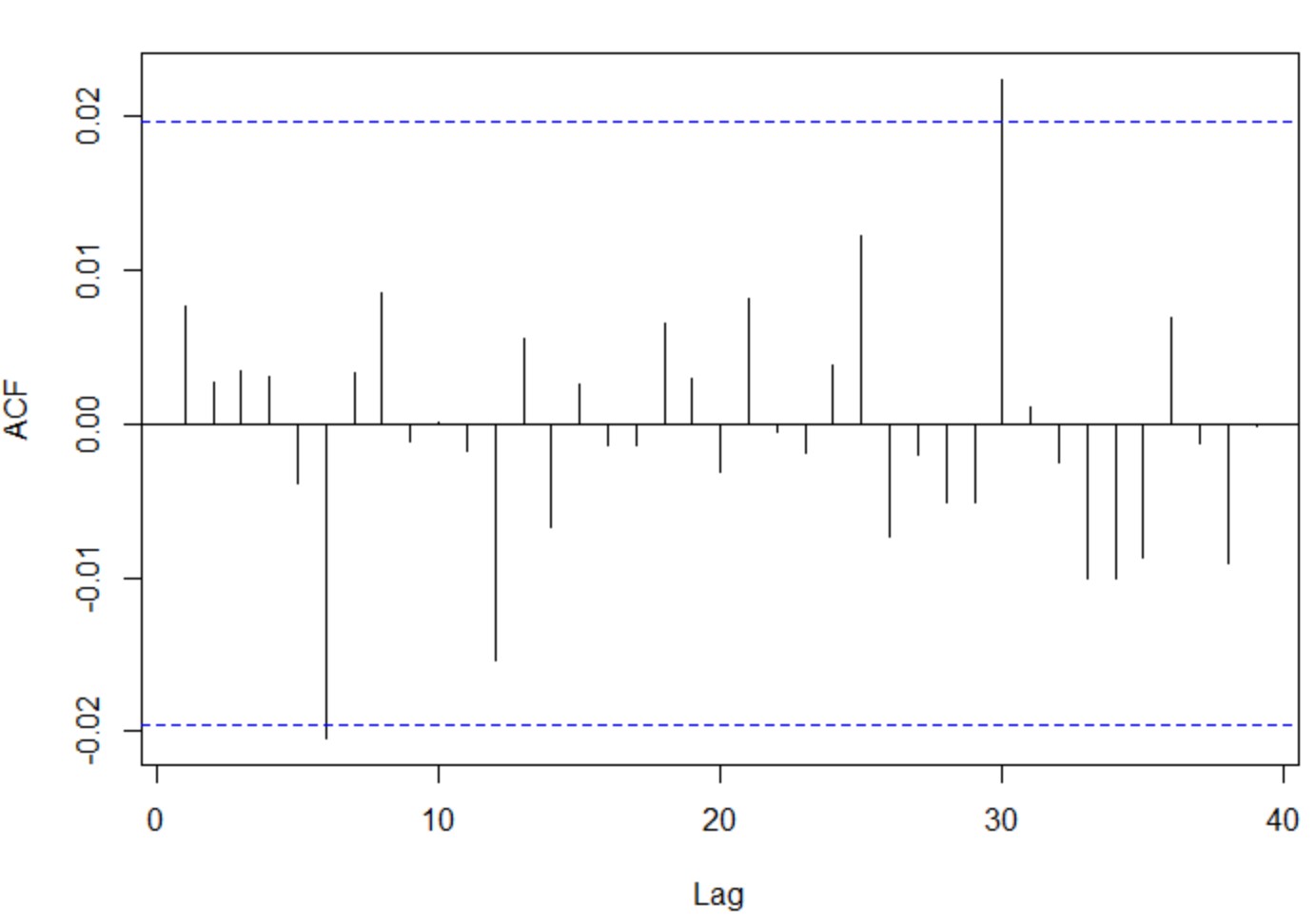
さらに、xの差分取ると、予想通りのwhite noiseが見えました。

話を少し拡張すると、確率微分方程式もただrandom walkの延長線にあります。

式右の第一項目はdrift項（よく0と仮定される）、右の第二項目のBはrandom walkの特殊型であるWiener過程です。

＝＞まさにrandom walk　<= Black-Scholes方程式の仮定（プライスがWiener過程に従う）

ARIMAモデルの選定

これらのモデルについての紹介が沢山ありますので、基本のコンセプトを簡単にまとめ、モデルの検証手順に重みをつけます。

PythonやRなどのライブラリには、既にauto arimaのような自動的に「最適」order数を探し出せる関数がありますが、本当の最適とは限らないです。

↓

orderが探すルールはrule of thumbのところが多いし、メインな評価指標である「AIC」や「BIC」そもそも複数モデル間の性能比較指標ではあり、モデル自体の正しさを評価しないです。

なので、マニュアルでモデルを探すことがよく進めらています。

例えば、R言語の[forecast]パッケージがモデル選定について、分かりやすいイラストが記載されています。

8.7 ARIMA modelling in R | Forecasting: Principles and Practice (2nd ed) (otexts.com)

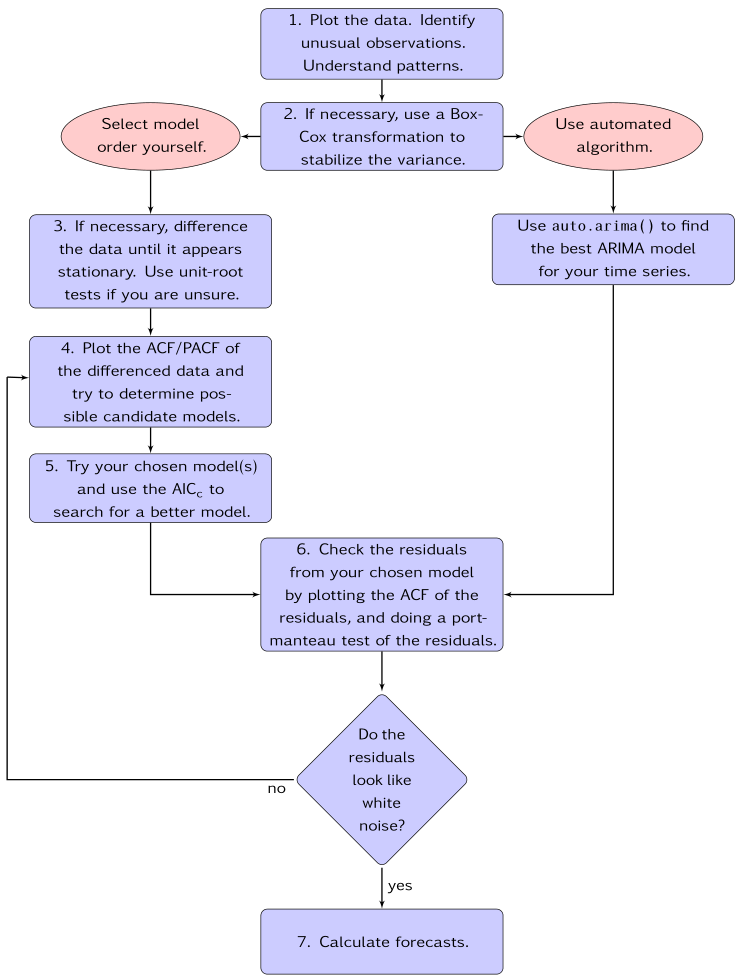
どんな訓練データ（input）が必要？

今回はUSD/JPYを分析対象にしました。yahoo financeからdailyのプライスを抽出しました。

Yahoo Finance – Stock Market Live, Quotes, Business & Finance News

まず、時系列データの季節性trendあるかどうかチェックします

from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt 
import seaborn as sns
import pylab
sns.set()

pylab.rcParams['figure.figsize'] = (14, 9)
dec = seasonal_decompose(df.Close, model = "additive")
dec.plot()
plt.show()

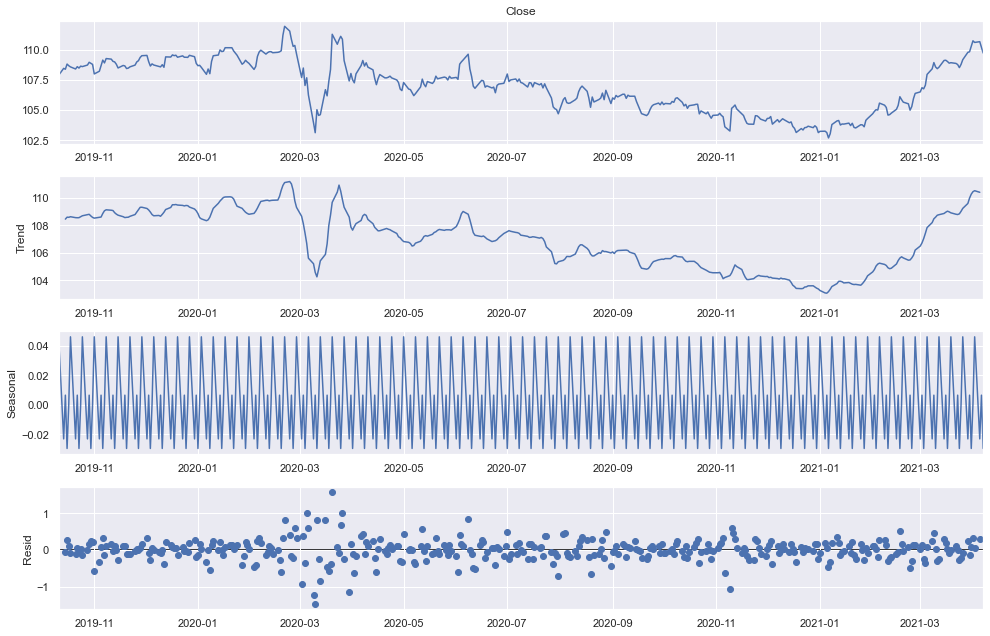
プライスが上記のように三つの成分に分けられました（Trend + Seasonal + Residual）。

seasonalみれば、明らかな変化がなく、定常的に-0.02~0.04くらいスイッチし、季節性がないと見えます。また、2月~4月のコロナショックも誤差のグラフで反映されていますね。

次は、この前のセクションで紹介したように、非定常過程の時系列データがモデリングできないです。グラフにも確認できますが、今回はADF test（unit root test）よりデータの定常性をテストします。

library(aTSA)
adf.test(df$Close)

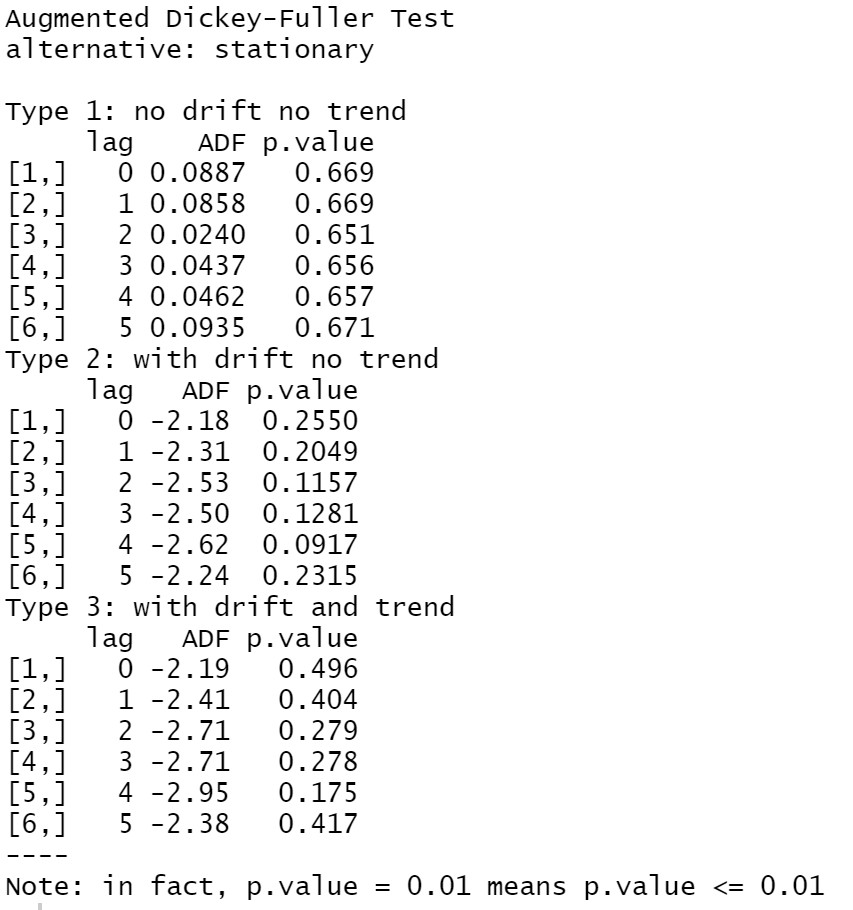
どのタイプのモデルでもp valueが0.1より大きいので、データが非定常過程という結論になります。

但し、時系列データをモデリングするため、定常過程に変換する必要があります。

＝＞　金融分野は基本的はリターン（log_return）という指標を使います

USD/JPYのlog_returnをADF testすると、

adf.test(df$log_return)

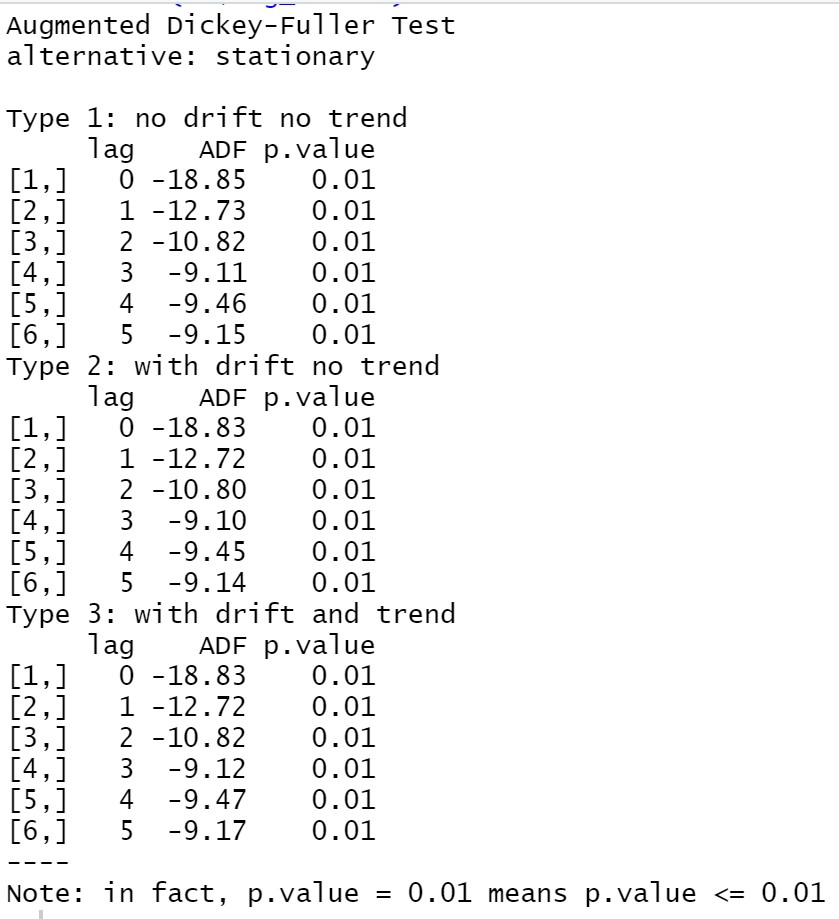
P valueが0.01より小さいので、プライスのreturnが定常過程ということが判りました。

それでは、log_returnをインプットとしてモデルに投入します。

モデルのorderをどう決めるか？

ACFかPACFを見て、判断します。式からわかると思いますが、

• AR(p):

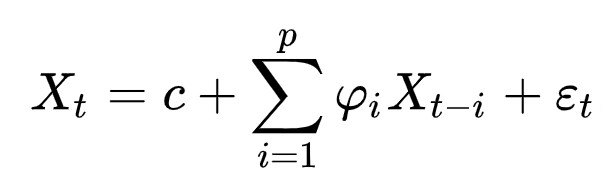
• MA(q):

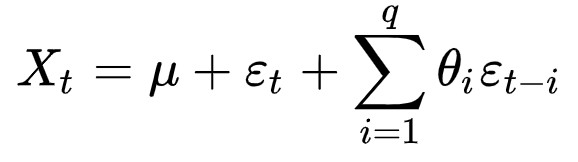
ARモデルは過去値との直接相関を見たいので　→　PCAF

MAモデルは過去値に依存しなく、どのlagの直接相関が高いという情報も重要ではないので　→　ACF

ARを例として、まずデータのPACF見てみる

sgt.plot_pacf(df.log_return[1:], lags = 40, zero = False, method = ('ols'))
plt.show()

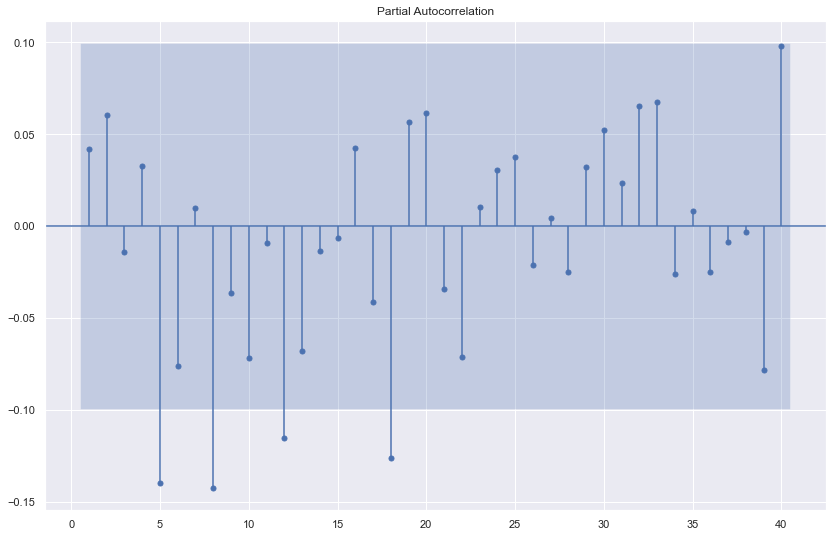
lag_5、lag_8…などが有意差（自己相関）が見えました。

simpleがいいというルールもありますので、まずlag_5のモデル→AR(5)から試します。

def arima_with_llr_test(df, ar, ma):
    model = ARIMA (df.log_return, order = (ar,0,ma))
    results = model.fit()
    print(results.summary())
    if ar>1:
        model_pre = ARIMA (df.log_return, order = (ar-1,0,ma))
        results_pre = model_pre.fit()
        print("LLR test: " + str(LLR_test(model_pre, model)))
    elif ma>1:
        model_pre = ARIMA (df.log_return, order = (ar,0,ma-1))
        results_pre = model_pre.fit()        
        print("LLR test: " + str(LLR_test(model_pre, model)))
arima_with_llr_test(df, 5, 0)

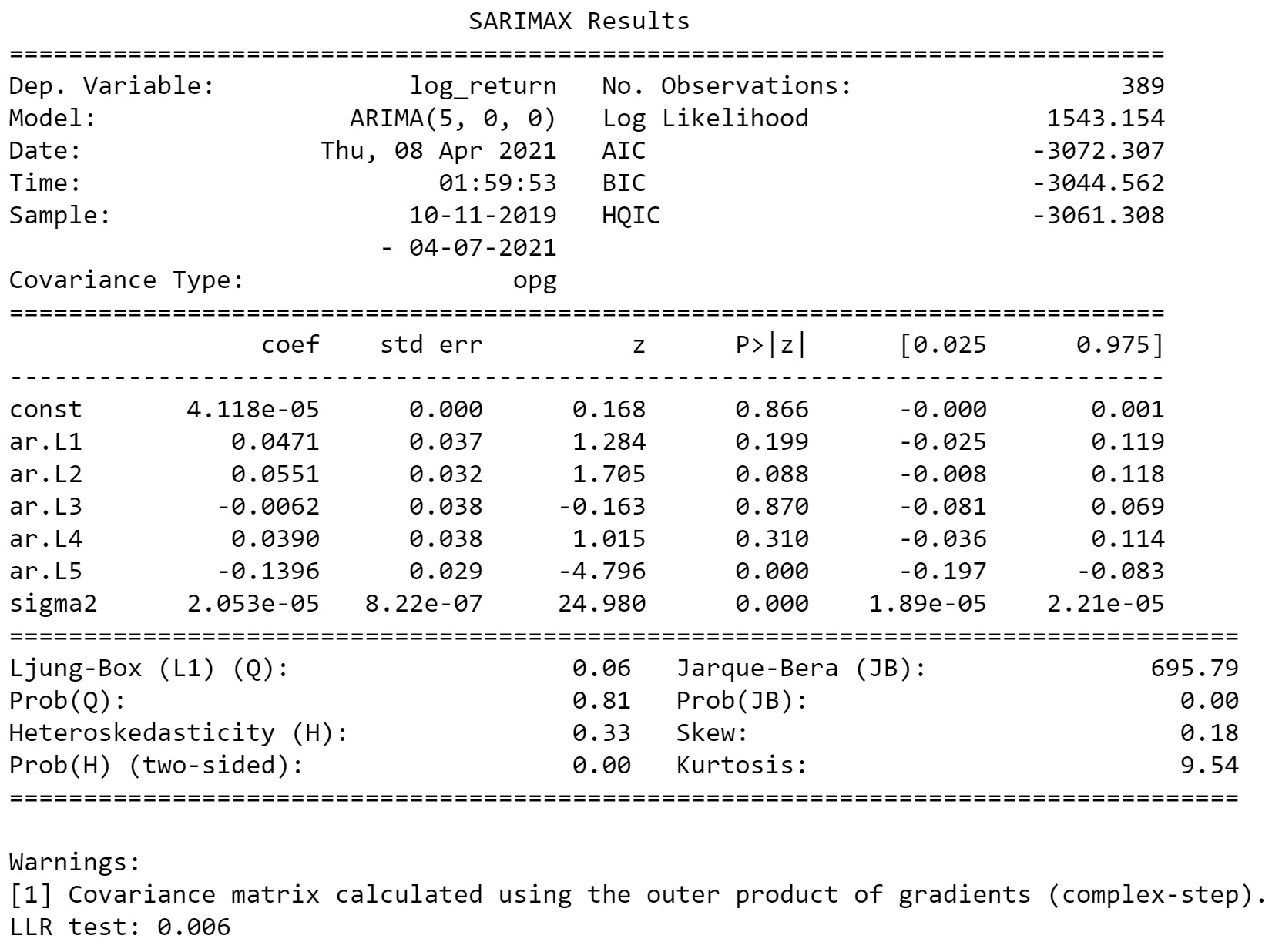
LLR_test（F test）のP valueが0.006なので、AR(4)よりAR(5)がいいというテストが通過しました。

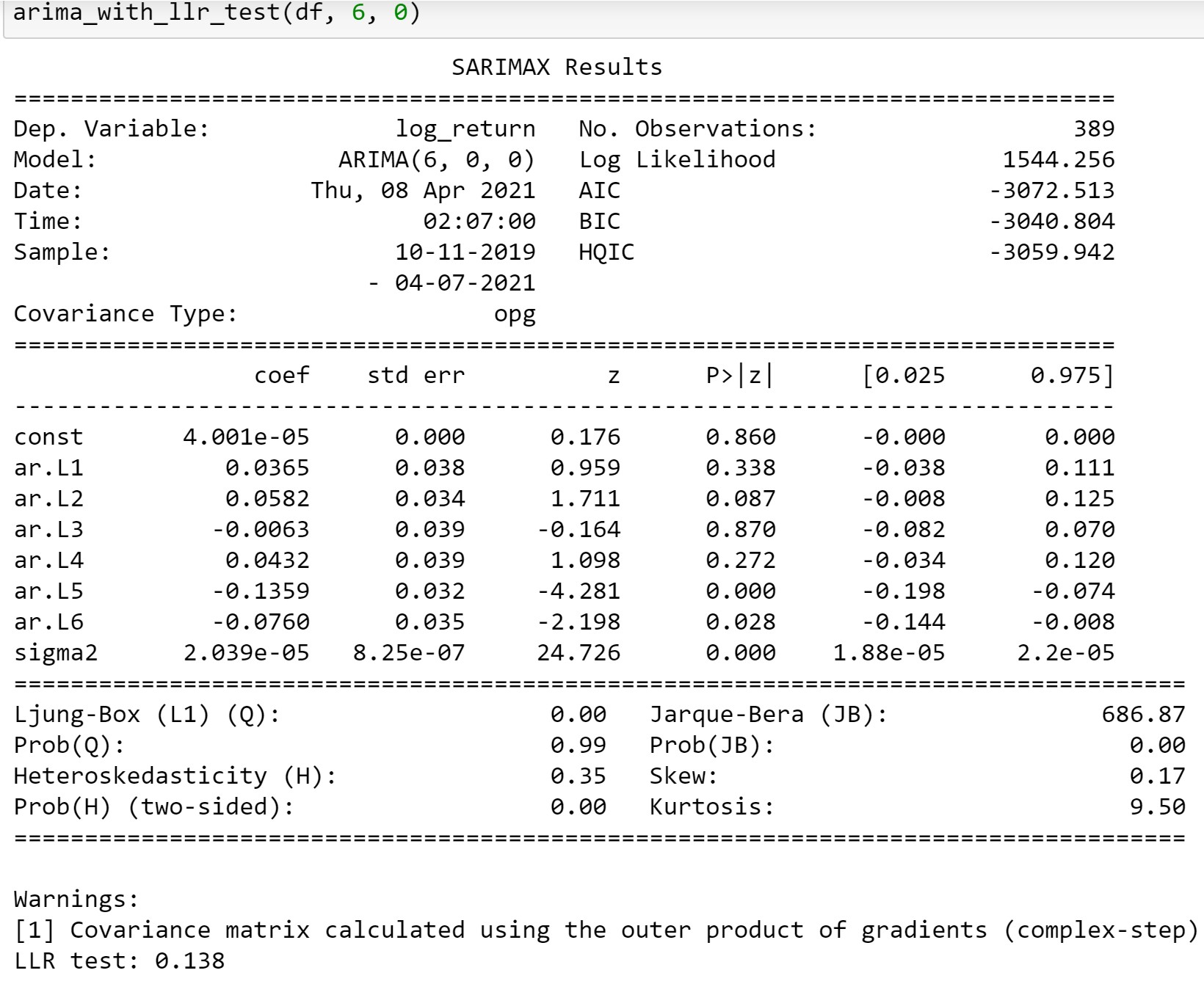
LLR_testが通過しないので、AR(6)がAR(5)よりいいといえません。

いいモデルが作ったのか？

この前にresidualを紹介したように、もしいい時系列モデルが作れば、データの相関関係はモデルよりうまく説明できるはずので、誤差の部分はwhite noiseになります。

↓

つまり、もしresidualがwhite noiseでなければ、モデルは問題あります。

それでは、上記のAR(5)モデル見てみます。

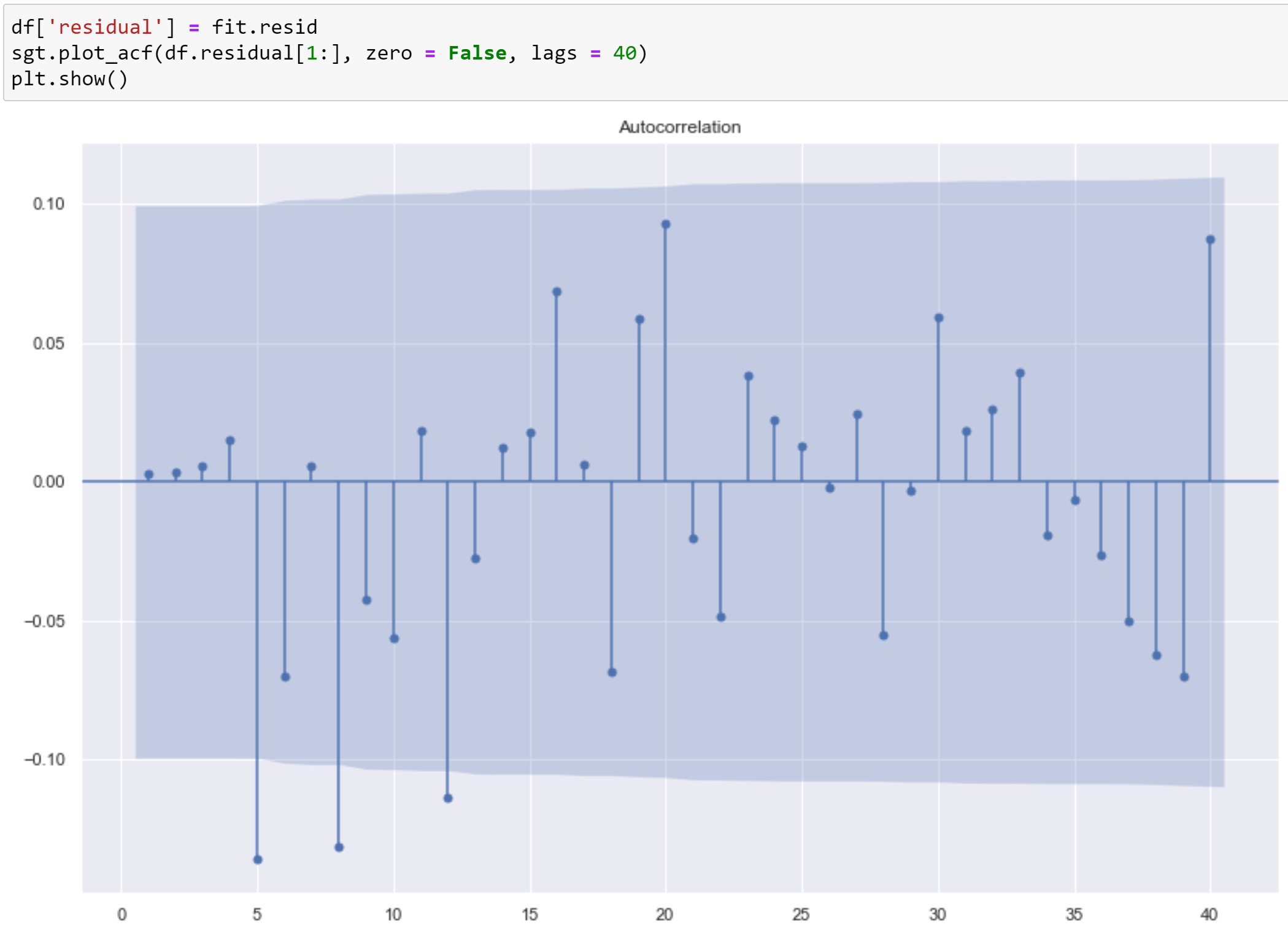
低いlag（lag=5）から相関見えましたので、white noiseではなさそうですね。

もうちょっと詳細の誤差見ると

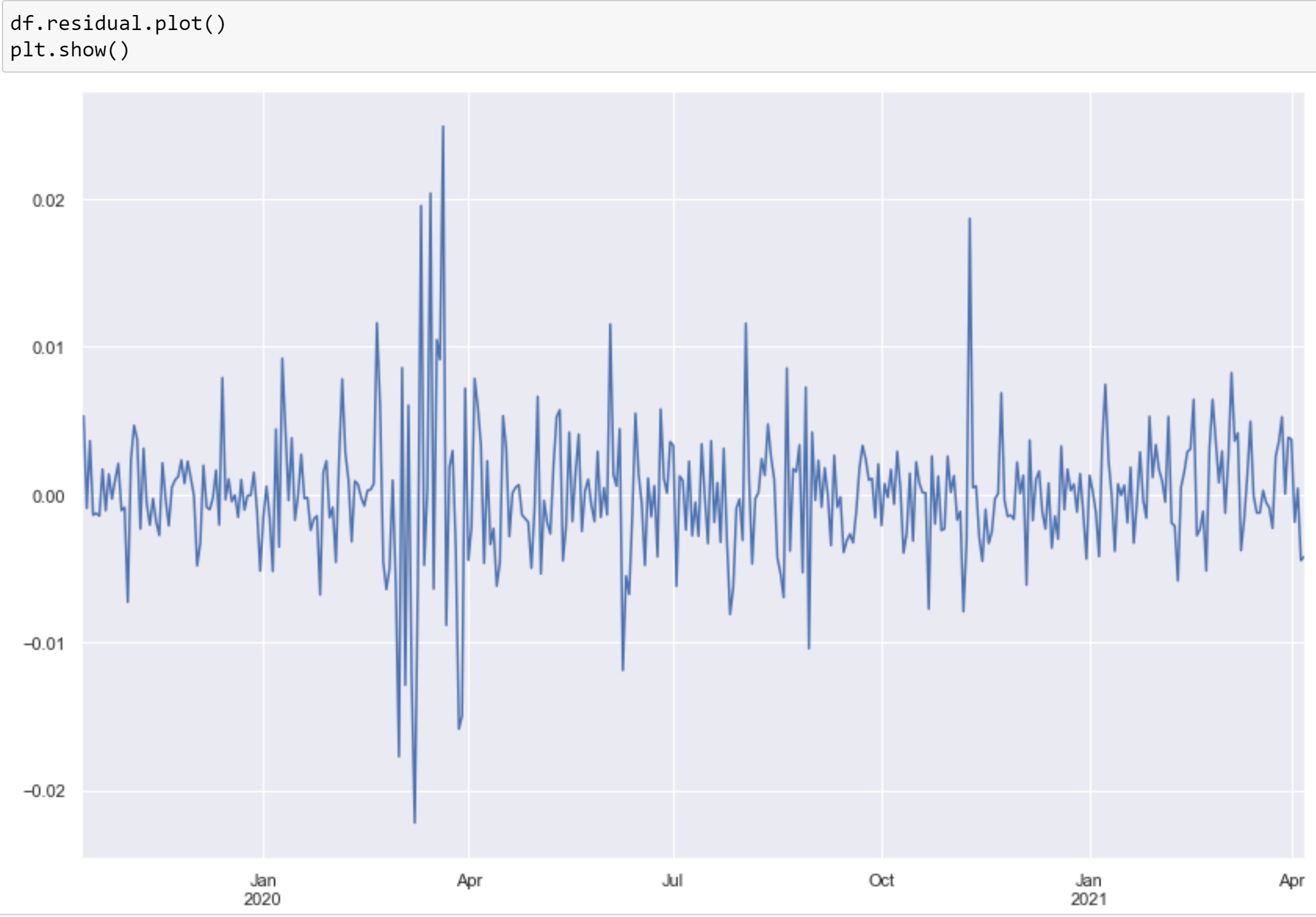
やはりコロナショックの影響を大きく受けているようです。

ARMA・ARIMA且つコロナショック

• ARMA(p,q)

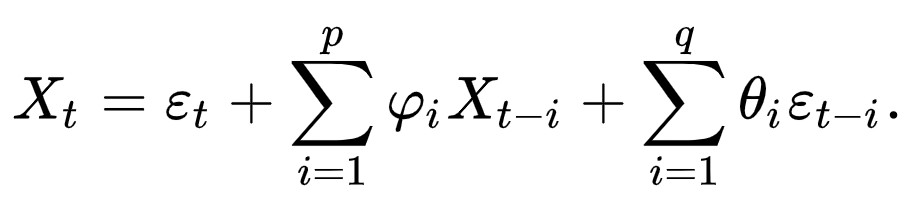
ARMAはただARモデルとMAモデルの組み合わせになります。ARとMA両方存在しますので、AICやBICの比較はできますが、LLRテストが実施できなくなりました。

ARIMAはARMAの上でさらに非定常過程から定常過程に変換するための項目を追加しました。というわけで、定常過程の時系列データについて通常はIが必要ないです。

しかし、ARMAでもコロナショックのような相場を上手にモデリングすることが恐らく難しいだろう。なぜかというと、ARIMA系のモデルはボラティリティが不変という仮定をしました。しかし、現実の世界ではvolatility clusteringの現象が存在しますので、constantなボラティリティが存在しません。

それを解決するため、次のGARCHモデルが出てきました。

GARCHモデルの概要

今回紙幅の関係で詳細に述べることはできないですので、

一言で言えば、GARCH系モデルはARMAの思想を借りてボラティリティのモデリングもしました。

ARCH系が今まで沢山な拡張版が提出されて、細かい改善が進めつつあります。

以下は前のUSD/JPYデータを使って、軽くGARCHモデルの選択をやってみました。

• モデルの紹介

Introduction_to_the_rugarch_package.pdf (r-project.org)

• 上記ライブラリによるモデル選択

library(readr)
library(tidyverse)
library(purrr)


max_lag_AR <- 1 
max_lag_MA <- 1 
max_lag_ARCH <- 2 
max_lag_GARCH <- 1 
dist_to_use <- c('norm', 'std') 
models_to_estimate <- c('sGARCH', 'eGARCH', 'gjrGARCH') 

graphics.off()

my_d <- dirname(rstudioapi::getActiveDocumentContext()$path)
setwd(my_d)

source('fcts/garch_fcts.R')

df <- read_csv("data/usdjpy.csv")
df <- as.data.frame(df)
df$Date <- as.Date(df$Date, format =  "%Y/%m/%d")
log_return <- diff(log(df$Close))
df = df[-1,]
df$log_return <- log_return

out <- find_best_arch_model(x = df$log_return, 
                            type_models = models_to_estimate,
                            dist_to_use = dist_to_use,
                            max_lag_AR = max_lag_AR,
                            max_lag_MA = max_lag_MA,
                            max_lag_ARCH = max_lag_ARCH,
                            max_lag_GARCH = max_lag_GARCH)


tab_out <- out$tab_out

df_long <- tidyr::pivot_longer(data = tab_out %>%
                                 select(model_name,
                                        type_model,
                                        type_dist,
                                        AIC, BIC),  cols = c('AIC', 'BIC'))

models_names <- unique(df_long$model_name)
best_models <- c(tab_out$model_name[which.min(tab_out$AIC)],
                 tab_out$model_name[which.min(tab_out$BIC)])

df_long <- df_long %>%
  mutate(order_model = if_else(model_name %in% best_models, 'Best Model', 'Not Best Model') ) %>%
  na.omit()

df_best_models <- df_long %>%
  group_by(name) %>%
  summarise(model_name = model_name[which.min(value)],
            value = value[which.min(value)],
            type_model = type_model[which.min(value)])

p1 <- ggplot(df_long %>%
               arrange(type_model), 
             aes(x = reorder(model_name, 
                             order(type_model)),
                 y = value, 
                 shape = type_dist,
                 color = type_model)) + 
  geom_point(size = 3.5, alpha = 0.65) + 
  coord_flip() + 
  theme_bw(base_family = "TT Times New Roman") + 
  facet_wrap(~name, scales = 'free_x') + 
  geom_point(data = df_best_models, mapping = aes(x = reorder(model_name, 
                                                              order(type_model)),
                                                  y = value), 
             color = 'blue', size = 5, shape = 8) +
  labs(title = 'Selecting Garch Models by Fitness Criteria', 
       subtitle = 'The best model is the one with lowest AIC or BIC (with star)',
       x = '',
       y = 'Value of Fitness Criteria',
       shape = 'Type of Dist.',
       color = 'Type of Model') + 
  theme(legend.position = "right")

x11()  ; p1

 

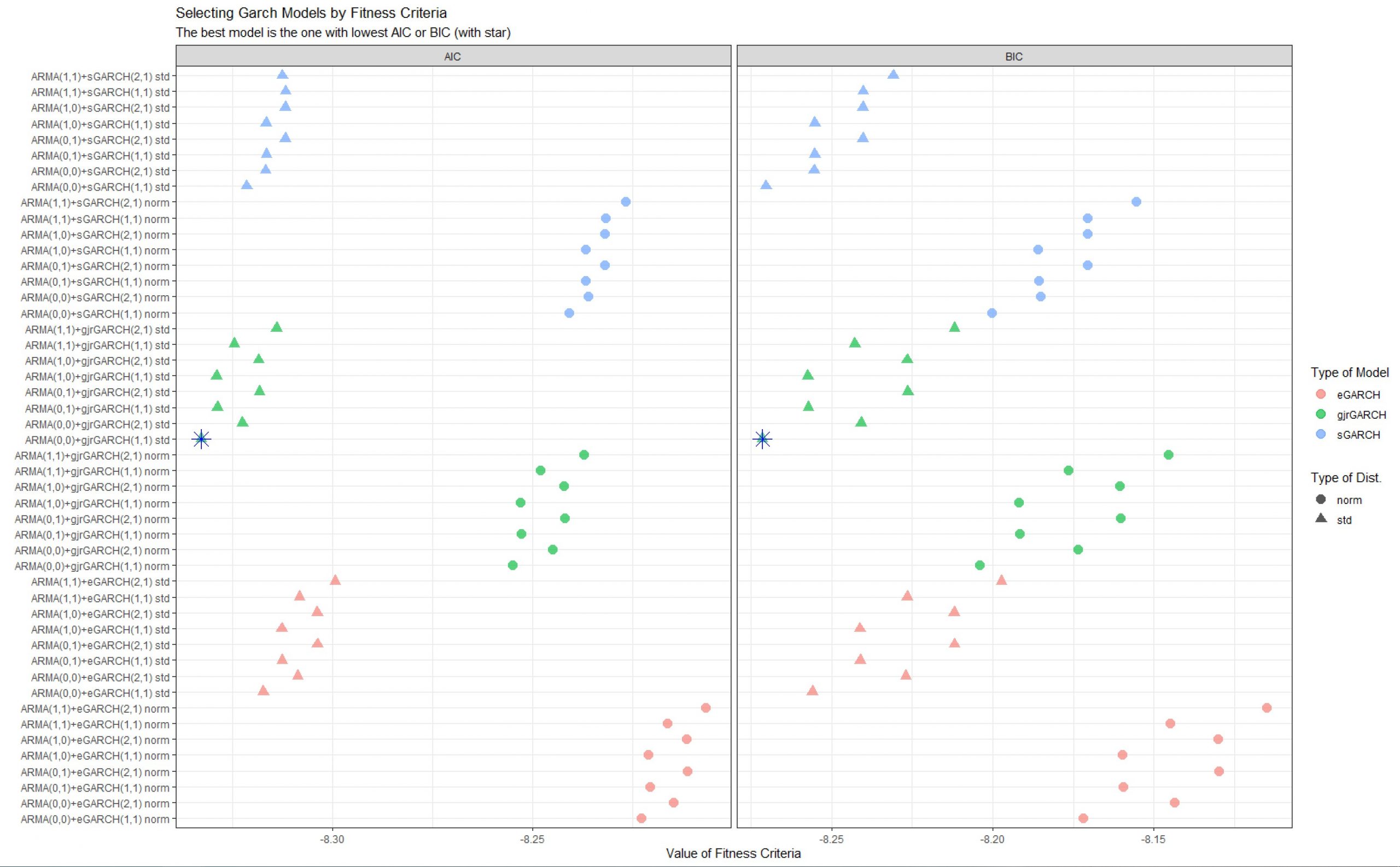
AICでもBICでも同じモデルに辿りました。（分布は正規分布とT分布を見ました）

さいごに

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。