[mathjax]

はじめまして、次世代システム研究室のY.T.と申します。
AIを使ったトレーディングとスイーツ作りが趣味です。最近は、バゲット系のパン作りにもチャレンジしています。
さて今回は、エンジニアのための金融工学入門というお題で、「Value at Risk」を取り上げたいと思います。

本エントリで紹介するJupyterNotebookは、以下からダウンロードできます。
【ダウンロード】blog-2017-1Q-fintech-value-at-risk-release

資産運用で大事なリスク管理

資産運用で大事なことは何でしょうか？

「マーケットの先を読んで、相場を張って勝負に勝つこと！」と考える方が多いのではないかと思います。

しかし、マーケットの未来を読んで勝負に勝つということは、世界的に有名なヘッジファンドマネージャー、ジョージ・ソロス（※１）であっても易しいものではありません。

大きく勝つこともあれば、逆に負けることもあります。
ましてや我々一般人にとっては、非常に困難であり、ギャンブル・博打となるのは火を見るよりも明らかです。

では、資産運用では何を大事にすればよいのでしょうか？

それは「最悪の事態に備え、生き延びること」であると筆者は考えています。

資産を溶かさず（※２）、生き延び続けることができれば、少しずつ資産を増やしていけるわけです。

しかも、資産運用は福利運用ですから、1年にほんの１パーセントであっても、それが指数関数的に効果をもたらします。
無理をして大きく勝つのではなく、しぶとく生き延びるというのが確実かつ賢明な戦略となります。

「Value at Risk（バリューアットリスク）」でリスクを測る

生き延びるために重要な第一歩は、どんなリスクが起こりうるのか前もって把握することです。
リスクとは具体的には、どれくらいの損失が発生しうるか、その額を見積ったものです。
リスクの計測に使われているのが、「Value at Risk」という指標なのです。

イメージを使って説明します。
まずは以下の画像をご覧ください。これは、QQQというナスダック指標ETFを1日保有した場合の損益の分布です。
釣鐘のような形（＝ベル・シェープ）をしています。
ここでは、QQQの1日保有の損益が、正規分布に従うと仮定しています。
正規分布は自然界の至る所で見られる分布であり、物事を統計的に分析する際の第一歩となる確率分布です。

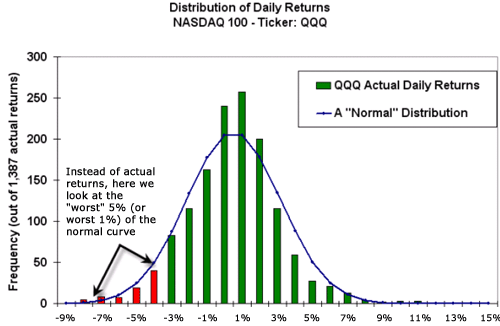
この損益分布の左側に焦点を当てます。
分布の棒グラフの色が赤くなっていますね。色の赤い部分は、特に損失が大きいことを現しています。
分布の縦軸は頻度ですから、とても低い確率であることが分かります。
起きる確率は低いですが、いったん起こると大変なダメージを被ってしまいます。

その大変なダメージはどれくらいなのか、数値化してみましょう。

赤い部分の右端は、損失が大きいほうから見て５％の位置にあります。
つまり、損失ランキング上位５％の位置というわけです。

具体的には約４．４％の損失をさしており、５％の確率で保有資産の約４．４％を失う事態が起きるということを意味します。

さらに赤い部分の左側に注目します。
損失が大きいほうから見て１％の位置、つまり損失ランキング上位１％の位置を見ると、約６．２％の損失になっています。

１％という低い確率で、保有資産の約６．２％を失う事態が起きることを意味します。

この「５％の確率で約４．４％の損失」や「１％の確率で約６．２％の損失」というのが、「Value at Risk」です。

一般的には、「信頼水準９５％のValue at Riskは約-4.4％」、「信頼水準９９％のValue at Riskは約-6.2％」といった言い方をします。

（１００％－信頼水準（％））が、リスクが発生する確率となっていることが分かります。

高い信頼水準のValue at Riskほど、よりレアな事態のリスクを指し示し、損失の見積額も大きなものになります。

一般的には、「信頼水準９５％のValue at Risk」および「信頼水準９９％のValue at Risk」が使われます。

Value at Risk の計算方法

Value at Riskを計算する方法には、現在大きく分けて３つのアプローチがあります。
それは「ヒストリカルシミュレーション法」「分散共分散法（デルタ法）」「モンテカルロシミュレーション法」の３つです。

それぞれの方法の特徴を簡潔に紹介します。

1.ヒストリカルシミュレーション法

現在、Value at Riskの計算方法として主流を占めている方法です。
過去のリスクファクター（＝株価や為替、金利の相場の値動き）のデータに基づいて保有資産の損益の分布を計算します。
そして信頼水準に該当する位置にある損失の値をValue at Riskとして採用します。

例：
信頼水準９５％のValue at Riskを求める場合、過去のマーケットにおける損益をソートして、
損失が大きい方から見て５％の位置にある値をValue at Riskとして採用します。

過去の値動きに基づいているため、損益分布の形状が正規分布でない場合でも適用できます。
その一方、過去の値動きに偏った傾向が反映されるため、最近の傾向にそぐわない可能性があります。

2.分散共分散法（デルタ法）

デルタ法とも呼ばれる方法です。
リスクファクターが正規分布に従い、なおかつリスクファクターと保有資産の変化率の関係が一定（＝デルタが一定）とみなして計算します。

デルタは感応度を表しており、
$$Δ=\frac{Δ_{value}}{Δ_{riskfactor}}=一定\\
\\
Δ_{value} : 資産価値の変化量\\
Δ_{riskfactor} : リスクファクターの変化量$$
とみなしてValue at Riskを求めます。

たとえば、リスクファクターとして株価を選びます。
株価が1％上がると、保有資産が0.75％増えるとします。
このとき、

$$Δ＝\frac{Δ_{value}}{Δ_{stock}} = \frac{0.75%}{1.0%} = 0.75\\
\\
Δ_{value} : 資産価値の変化量\\
Δ_{stock} : 株価の変化量$$
となります。

絶対的変化量ではなく、パーセントを用いた相対的変化量を使ってΔを計算するところに注意してください。

こうして計算式に代入するだけでValue at Riskを算出できるため、処理は高速です。

$$ValueAtRisk = 信頼係数 \times Δ \times σ \\
Δ : 感応度\\
σ : 過去のデータにおける損益分布から求めた標準偏差 $$

信頼係数は、信頼水準ごとに決まっています。
信頼水準９９％の場合は、2.33です。
正規分布を使った両側検定の確率分布ではなく、片側検定の確率分布から求めた係数です。
なお両側検定の場合、信頼水準９９％の信頼係数は2.58です。

また、金融資産の保有期間を変えたり、複数の金融資産を保有する場合のValue at Riskも計算式に代入して求めることができるというメリットがあります。

一方、分散共分散法の弱点は、損益の分布を正規分布と仮定していることにあります。
実際には正規分布ではないリスクファクターの動きもあるため、実体と乖離したValue at Riskになる恐れがあります。
また、Δが一定ではない場合（＝非線形リスク）も現実には起こりうるので、近似的な計算で対処せざるを得ないという弱点があります。

3.モンテカルロシミュレーション法

乱数を用いてリスクファクターの変動をシミュレーションし、保有資産の損益の分布を計算してValue at Riskを求めます。
リスクファクターの変動パターンの再現に正規分布だけではなく、他の確率分布も適用することができます。
また、分散共分散法で問題となっていたΔが一定ではないケース（＝非線形リスクがある場合）にも対処できます。

ただし、リスクファクターがどのような振る舞いをするのか調べて、適切な確率分布を適用しなければ、精度が大きく悪化する恐れがあります。
-> 適切な確率分布を見極める職人芸が求められる局面がありえます。

また、複雑な資産構成で大量の計算をする場合、計算負荷が重くなり、Value at Riskを得るのにかなり時間がかかってしまいます。

実際にValue at Risk を計算してみる

1.ヒストリカルシミュレーション法

それでは実際にプログラムを使ってヒストリカルシミュレーション法でValue at Riskを計算してみましょう。
外国為替市場のドル円を題材としてValue at Riskを計算します。
ここではJupyterNotebookを使い、Pythonで計算をします。
実験用に用意したドル円のヒストリカルデータ usdjpy_2001_2017.csv を読み込みます。
【データダウンロード】usdjpy_2001_2017

2016年以前のデータを対象に計算をして、2016年のリスクを予測します。

まず、終値(カラム’close’の値)を基準に、1日保有したときの損益を求めます。
つまり、前日の終値との差です。

%matplotlib inline
import numpy as np
import matplotlib
import math
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from numpy.random import *
import pandas as pd

font_path = 'C:/Windows/Fonts/meiryo.ttc'
font_prop = FontProperties(fname=font_path)
matplotlib.rcParams['font.family'] = font_prop.get_name()

fp = FontProperties( fname=font_path, size=14)
df = pd.read_csv("./usdjpy_2001_2017.csv")

# 読み込んだばかりの状態では object型なので、ここでdatetime型に戻しておく
df['date'] = pd.to_datetime(df['date'])

# 2016年以前のものに絞り込む
df = df[df['date'] < '2016-01-01']

# 差分を取る＝損益
df['diff'] = df['close'].diff(periods=1)

せっかくなので、損益の分布の形を見てみましょう。

df['diff'] = df['diff'].fillna(0)
plt.figure()
df['diff'].plot.hist(bins=100)
plt.xlabel(u'前日との差',fontproperties=fp)
plt.ylabel(u'頻度',fontproperties=fp)

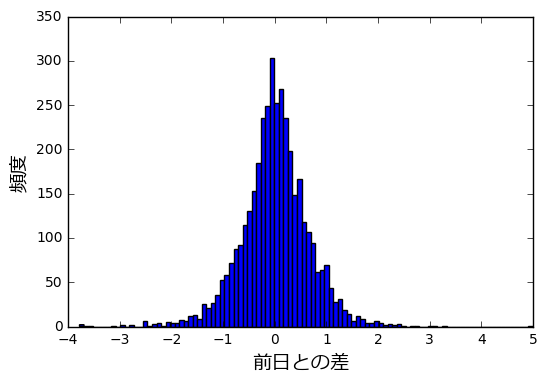
釣鐘のような形をしていることが分かります。
統計ではおなじみの正規分布に近い形をしているように見えますね。

分散共分散法やモンテカルロ法では、この分布から求めた標準偏差を使うのですが、
ヒストリカルシミュレーション法では、標準偏差は使いません。
得られた損益(カラム’diff’)の値を大きい順に並べ、信頼水準に合わせて値をとってきます。

たとえば信頼水準９９％の場合、上から９９％の位置にある損益を採用します。
（言い換えれば、損失が大きいほうから見て上位１％の位置にあります）

df['diff'].quantile(1.0-0.99)

# 実行結果
-1.8260000000000076

つまり、ヒストリカルシミュレーション法で求めた Value at Riskは　-1.826円であり、
終値ベースで見てドル円が一日で 1.826円下落するリスクを見積もる必要がある、という意味になります。

使い方としては、「1.826円下落しても大丈夫なように、保有するポジションの量を減らす」といった対応が例として挙げられます。

2.分散共分散法(デルタ法)

続いて分散共分散法でValue at Riskを計算してみましょう。
分散共分散法では、リスクファクターの動きが正規分布に従うと仮定して計算します。
ヒストリカルシミュレーション法と同じく、外国為替市場のドル円相場のデータを使って実験をしたいと思います。

2016年以前のデータを対象に、1日保有した場合の終値ベースの差分を計算します。

df = pd.read_csv("./usdjpy_2001_2017.csv")

# 読み込んだばかりの状態では object型なので、ここでdatetime型に戻しておく
df['date'] = pd.to_datetime(df['date'])

# 2016年以前のものに絞り込む
df = df[df['date'] < '2016-01-01']

# 差分を取る＝損益
df['diff'] = df['close'].diff(periods=1)

では、損益の分布を計算し、標準偏差σを求めましょう。

df['diff'].std()

# 実行結果
0.6690693466453383

標準偏差σを計算できました。

分散共分散法では、リスクファクターが平均０、標準偏差σの正規分布に従うと仮定しました。
実際の平均値はどうなっているか確かめてみましょう。

print df['diff'].mean()

# 実行結果
0.0014783388874647515

0.147％です。０％に近い値になっていることが分かります。

それでは Value at Risk を求めましょう。
分散共分散法におけるValue at Riskの計算式は以下のとおりです。

$$ValueAtRisk = 信頼係数 \times Δ \times σ\\
Δ：感応度$$

ここでは、Δ（感応度）=1.0 とします。
すなわち、ドル円相場が動けば、連動して資産価格も変動すると仮定します。

９９％の信頼水準を適用すると、Value at Risk は、以下のようになります。

$$Value at Risk \\
= 2.33 \times 1.0 \times 0.6690693466453383 \\
= 1.5589315776836383 \\
≒ 1.559 (円)$$

すなわち、1日で1.559円下落するリスクがあるということが示されました。
ヒストリカルシミュレーション法の場合と比べると、リスクの見積もり幅が少し浅くなっています。

　ヒストリカルシミュレーション法のValue at Risk = 1.826円

Value at Riskを計算式に代入するだけで求めることができますが、ややリスクの見積もり量が少し小さいですね。
一長一短といったところですが、分散共分散法にはもう一つメリットがあります。

複数の金融資産から構成されるポートフォリオ（＝リスクファクターが複数）のリスク測定も、計算式一つで可能という点です。

具体的には、共分散行列を使うことで、計算式一つでValue at Riskを算出します。

なおヒストリカルシミュレーション法で求める場合、各資産の推移を実際に計測して記録を蓄積してから、ようやくValue at Riskを求めるという手間がかかります。

それでは、ポートフォリオのリスクを分散共分散法で実際に計算して見ましょう。
リスクファクターとして、これまでのドル円に加え、金相場の価格を加えます。
ドル円と同じく日足データを使います。

ゴールド価格は、ワールドゴールドカウンシルの公式サイトからダウンロードできます。
http://www.gold.org/research/download-the-gold-price-since-1978

ゴールド価格（単位：ドル）の1日の変化量がどのような分布をしているのか、まず確認します。
ドル円の時と同様に、JupyterNotebookを使い、CSVファイルを読み込みヒストグラムを描画します。
ワールドゴールドカウンシルから入手したゴールド価格のデータを加工して作成した xau_usd_2001_2017.csv を読み込みます。
【データダウンロード】xau_usd_2001_2017

# ゴールド価格の読み込み
df_gold = pd.read_csv("./xau_usd_2001_2017.csv")
df_gold['date'] = pd.to_datetime(df_gold['date'])

df_gold = df_gold[df_gold['date'] < '2016-01-01']

# 差分を取る
df_gold['diff'] = df_gold['close'].diff(periods=1)

plt.figure()
df_gold['diff'].plot.hist(bins=100)
plt.xlabel(u'前日との差',fontproperties=fp)
plt.ylabel(u'頻度',fontproperties=fp)
plt.title(u'ゴールド価格の変化量の分布',fontproperties=fp)

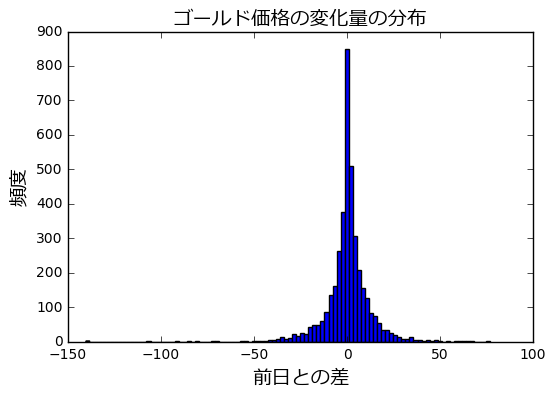
ドル円と比べると、尖った形の分布をしています。

では、ドル円とゴールドから構成される資産ポートフォリオを組んで、その資産価値の推移を見て見ましょう。

• 測定期間：2015年1月～2015年12月
• 資産構成：ドル100億円分、ゴールド100億円分
• リスク見積条件：ポートフォリオを1日保有するときに生じうる損失の大きさ
  -> これをValue at Risk として計算します。

ドル円とゴールド価格の値動き履歴のCSVファイルを読み込み、2015年1月～2015年12月を取り出し、
営業日初日の価格からドルとゴールドの購入量を計算します。

# ドル円相場データの読み込み
df_usdjpy = pd.read_csv("./usdjpy_2001_2017.csv")
df_usdjpy['date'] = pd.to_datetime(df_usdjpy['date'])

# 2015年1月～12月の範囲を取り出す
df_usdjpy = df_usdjpy[(df_usdjpy['date'] < '2016-01-01') & (df_usdjpy['date'] > '2015-01-01')]

# ゴールド価格の読み込み
df_gold = pd.read_csv("./xau_usd_2001_2017.csv")
df_gold['date'] = pd.to_datetime(df_gold['date'])

# 2015年1月～12月の範囲を取り出す
df_gold = df_gold[(df_gold['date'] < '2016-01-01') & (df_gold['date'] > '2015-01-01')]

df_usdjpy = df_usdjpy.set_index('date')
df_gold = df_gold.set_index('date')

# 最初の日の相場を取り出す
first_index = df_usdjpy.index[0]

first_usdjpy = df_usdjpy.ix[first_index]
first_gold = df_gold.ix[first_index]

# 保有資産はそれぞれ100億円分でスタート
start_value = 100 * 100000000

# 初日の終値から購入量を計算する
# 100億円 ÷ 終値 = 資産購入量
amount_usd  = start_value * 1.0 / first_usdjpy['close']
amount_gold = start_value * 1.0 / ( first_gold['close'] * first_usdjpy['close'] )

すると、ドル購入量、ゴールド購入量が以下のようになります。

print "ドル購入量(100億円分) = %d ドル" % (amount_usd)
print "ゴールド購入量(100億円分) = %d オンス" % (amount_gold)

# 実行結果
ドル購入量(100億円分) = 83043373 ドル
ゴールド購入量(100億円分) = 70856 オンス

この購入量に基づいて、ポートフォリオ価値（ドルの価値＋ゴールドの価値）の推移を見ていきましょう。
ドル円価格のデータフレームの日付インデックスに基づいて、ループ処理を実施します。
各営業日ごとにポートフォリオ価値を計算し、その履歴をデータフレームに記録していきます。

# ポートフォリオ価値の推移を記録する。
# date      : 日付
# pf_value  : 円換算時のポートフォリオ価値
# usdjpy    : ドル円価格
# gold_usd  : 金価格(ドル換算)
# gold_jpy  : 金価格(円換算)
pf_history = pd.DataFrame(columns=['date','pf_value','usdjpy','gold_usd','gold_jpy'])
for index_cursor in df_usdjpy.index:
    # 各日付におけるポートフォリオ価値の計算
    each_pf_value = amount_usd * df_usdjpy['close'][index_cursor] + \
                    amount_gold * df_usdjpy['close'][index_cursor] * df_gold['close'][index_cursor]
    
    print "%s  pf_value=%s" % (index_cursor,each_pf_value)
    # ポートフォリオ価値の推移を記録する
    pf_history = pf_history.append( pd.DataFrame([[index_cursor,each_pf_value,df_usdjpy['close'][index_cursor],df_usdjpy['close'][index_cursor],
                                     df_usdjpy['close'][index_cursor] * df_gold['close'][index_cursor]]],
                                    columns=['date','pf_value','usdjpy','gold_usd','gold_jpy']))

すると、以下のような出力が得られます。
ポートフォリオ価値が200億円前後で推移していることが確認できます。

# 実行結果
2015-01-02 00:00:00  pf_value=20000000000.0
2015-01-05 00:00:00  pf_value=20105627770.1
2015-01-06 00:00:00  pf_value=19967415466.6
2015-01-07 00:00:00  pf_value=20129634567.8
2015-01-08 00:00:00  pf_value=20235825218.9
2015-01-09 00:00:00  pf_value=20044839793.9
2015-01-12 00:00:00  pf_value=20111524381.0
2015-01-13 00:00:00  pf_value=20082263070.5
2015-01-14 00:00:00  pf_value=20008494444.3
・・・中略・・・

さて、ここで各資産（ドルとゴールド）の1日ごとの価格の変化量を見てみましょう。
まず、diff()メソッドを使い1日ごとの変化量を求め、データフレームに新しい列として追加します。
すると、平均値は０付近（標準偏差の大きさに対して十分小さい）の分布を取ることが分かります。
標準偏差の5％未満になっています。

# 各資産価格の変化量の計算
pf_history['diff_usdjpy'] = pf_history['usdjpy'].diff(periods=1)
pf_history['diff_gold_usd'] = pf_history['gold_usd'].diff(periods=1)
pf_history['diff_gold_jpy'] = pf_history['gold_jpy'].diff(periods=1)

print "[USDJPY] 平均:%s    標準偏差(σ):%s" % ( pf_history['diff_usdjpy'].mean(),pf_history['diff_usdjpy'].std())
print "[ゴールド] 平均:%s    標準偏差(σ):%s" % ( pf_history['diff_gold_usd'].mean(),pf_history['diff_gold_usd'].std())
print "[ゴールド(円換算)] 平均:%s    標準偏差(σ):%s" % ( pf_history['diff_gold_jpy'].mean(),pf_history['diff_gold_jpy'].std())

# 実行結果
[USDJPY] 平均:-0.000821705426357    標準偏差(σ):0.621896383698
[ゴールド] 平均:-0.434108527132    標準偏差(σ):10.1231867464
[ゴールド(円換算)] 平均:-53.1459224806    標準偏差(σ):1203.38599955

信頼水準を９９％として、個々の資産価格ごとにValue at Riskを計算します。
感応率は1.0とします。
各資産のValue at Risk は以下のようになります。

　[USDJPY] 
　Value at Risk = 2.33 x 1.0 x 0.621896383698 = 1.449018574 ≒ 1.449 (円)
　
　[ゴールド] 
　Value ar Risk = 2.33 x 1.0 x 10.1231867464 = 23.58702512 ≒ 23.587(ドル)
　
　[ゴールド(円換算)]
　Value at Risk = 2.33 x 1.0 x 1203.38599955 = 2803.889379 ≒ 2803.889 (円)

各プロフィットファクター（USDJPY,ゴールド)をポートフォリオ価値に反映します。
最初に100億円分購入した各資産の量を、Value at Riskに掛けます。すると次のようになります。

　[Value at Risk:ドル資産]
　83043373 ドル x 1.449(円) = 120,329,847(円)
　
　[Value at Risk:ゴールド資産]
　70856 オンス x 2803.889(円) = 198,672,359(円)
　
　[Value at Risk:全体]
　120,329,847(円) + 198,672,359(円) = 319,002,206(円)

単純に計算すると、ドル資産とゴールド資産のValue at Riskを足し合わせて求めた 319,002,206(円)が
ポートフォリオ全体のValue at Risk であるように思えます。

しかし、本当にそうなるでしょうか？
実際に記録したポートフォリオ価値の推移からValue at Riskを計算してみましょう。

まず、ポートフォリオ全体の価値の平均値と標準偏差を求めます。
実行結果は次のようになります。

# ポートフォリオ全体の資産価格の変化量の計算
pf_history['diff_pf_value'] = pf_history['pf_value'].diff(periods=1)
print "[ポートフォリオ全体] 平均:%s    標準偏差(σ):%s" % ( pf_history['diff_pf_value'].mean(),pf_history['diff_pf_value'].std())

# 実行結果
[ポートフォリオ全体] 平均:-3833951.09292    標準偏差(σ):111043617.681

信頼水準９９％として、ポートフォリオ全体のValue at Risk を計算しましょう。
感応度は1.0とします。

　[Value at Risk:全体]
　Value at Risk = 2.33 x 1.0 x 111043617.681 ≒ 258,731,629(円)
　
　
　[補足] ちなみにヒストリカル法で求めると、259951119.62165439 = 259,951,119(円) になります。
　デルタ法で求めた Value at Risk の値とほぼ一緒ということが分かります(誤差:約0.47％)

ドル円とゴールドのそれぞれのValue at Riskを足した値 319,002,206(円)よりも小さな値になっていることが分かります。
これがいわゆる「ポートフォリオ効果」と呼ばれる現象です。

実際のリスクの大きさは、ポートフォリオを構成する各資産のリスクを合計した大きさより小さくなるという現象です。
リスクを減らすことができているわけです。

しかし、実際にポートフォリオを組んでマーケットでポジションを取らなければ、リスクを見積もることができないというのは困ります。
前もって予測できることが望ましいからです。

ポートフォリオを組み替えるたびに、実際に資金を投入し、経過を観察して計算データを集めるというのは非効率で危険です。
ポートフォリオを構成する各資産（＝リスクファクター）ごとの統計情報であれば、過去のデータから導くことができます。
それらを使って、ポートフォリオ全体のリスクを推測することができないでしょうか。

実は可能です。
　共分散行列を使うことで、実際にポートフォリオを組んで経過観察することなく、ポートフォリオ全体のリスクを見積もることができるのです。

2.1.分散共分散法：共分散行列を使ったポートフォリオ全体のValue At Riskの計算

それでは、共分散行列を使ってポートフォリオ全体のValue At Riskを計算します。
実際にポートフォリオを組む前に、Value At Riskを計算できることを確かめましょう。

まず共分散行列を求めます。

df_cov = pd.DataFrame(columns=["usdjpy","gold_jpy"])

# ドル資産価値の推移
df_cov['usdjpy'] = pf_history["usdjpy"] * amount_usd

# ゴールド資産価値の推移
df_cov['gold_jpy'] = pf_history["gold_jpy"] * amount_gold

# 変化量を計算する
df_cov['usdjpy'] = df_cov['usdjpy'].diff(periods=1).fillna(0)
df_cov['gold_jpy'] = df_cov['gold_jpy'].diff(periods=1).fillna(0)
cov_matrix = df_cov.cov()

cov_matrix の内容は以下のようになります。

               usdjpy      gold_jpy
usdjpy    2.791194e+16 -2.078559e+16
gold_jpy -2.078559e+16  1.708546e+17

ポートフォリオ全体の標準偏差は以下のようにして求めることができます。
$$σ_{portfolio} =\sqrt{ \left(
\begin{array}{ccc}
Δ_{usdjpy} & Δ_{goldjpy}
\end{array}
\right)
\left(
\begin{array}{ccc}
V_{usdjpy} & V_{usdjpy,goldjpy} \\
V_{usdjpy,goldjpy} & V_{goldjpy}
\end{array}
\right)
\left(
\begin{array}{ccc}
Δ_{usdjpy} \\
Δ_{goldjpy}
\end{array}
\right)
}
\\
σ_{portfolio} : ポートフォリオ全体の標準偏差 \\
Δ_{usdjpy} : ドル円の感応度。1.0 とする。\\
Δ_{goldjpy} : ドル円の感応度。1.0 とする。\\
V_{usdjpy} : ドル円資産の標準偏差\\
V_{goldjpy} : ゴールド資産(円換算)の標準偏差\\
V_{usdjpy,goldjpy} : ドル円資産とゴールド資産（円換算）の共分散
$$

感応度行列Δは、ドル円、ゴールドそれぞれの感応度を1.0として以下のように定義します。

delta = np.array([1,1]) 

numpy の行列計算メソッドを使うと以下のように計算することができます。

print np.sqrt(np.dot( np.dot(delta,cov_matrix),delta.T))

# 実行結果
110828463.98120596

すると、110828463.98120596 ≒ 110,828,464(円) という標準偏差が導かれます。
これに対して信頼水準99％の係数 2.33 をかけると、
ポートフォリオ全体のValue at Riskの値が計算されます。

$$ValueAtRisk_{portfolio}=110828463.98120596 \times 2.33 = 258230321.07620987 ≒ 258,230,321(円)$$

先ほど、実際のポートフォリオの資産額の推移から求めた Value at Riskと比較してみましょう。

　【実際の資産価格の推移から求めた Value at Risk】
　258,731,629(円)
　
　
　【共分散行列を使って求めた Value at Risk】
　258,230,321(円)

その差は、0.19％であり、ほぼ一致していることが分かります。

このように、ポートフォリオを構成する各資産（ドルやゴールド）の過去の値動きを使って、
これから組成するポートフォリオの未来のリスクを予測できるのです。

3.モンテカルロシミュレーション法

前の節では、デルタ法を用いて共分散行列からポートフォリオのリスクを計算できることをお伝えしました。
次に、モンテカルロシミュレーションを用いたリスクの計算方法を紹介します。

デルタ法では、感応度が一定であることを前提にリスクの計算をしていますが、実際には感応度が一定ではない「非線形」な変化を示す場合があります。
つまり、ポートフォリオを構成するリスクファクター（＝株価や為替相場）の変化と、ポートフォリオの資産の変化の対応が一定ではない場合です。

たとえば、ドル円が90円から100円までの間は感応度が1.0であったのに対して、100円を超えると感応度が急激に減少するケースが挙げられます。

感応度が途中で変化してしまうと、共分散行列を使ったリスクの見積もりの計算が成り立たなくなってしまいます。
リスクファクターとポートフォリオの資産価値の関係が一定ではない複雑な状況で、モンテカルロシミュレーションが威力を発揮します。

モンテカルロシミュレーションを実施するに先立ち、ポートフォリオを構成する各リスクファクターの振る舞いについて統計的に把握します。
「分布の種類」「平均値」「標準偏差」といった統計的情報を調べます。

まず、先ほどデルタ法の節で求めたゴールド価格(円換算)の分布を見てみましょう。

from numpy.random import *
# 正規分布かどうか調べる
avg_dist = pf_history['diff_gold_jpy'].mean()
std_dist = pf_history['diff_gold_jpy'].std() 
pf_history['replayed_norm_gold_jpy'] = normal(avg_dist,std_dist,len(pf_history.index))
    
pf_history.plot(y=['diff_gold_jpy','replayed_norm_gold_jpy'],kind='hist',bins=100,alpha=0.4,figsize=(16,8))
plt.xlabel(u'前日との差',fontproperties=fp)
plt.ylabel(u'頻度',fontproperties=fp)
plt.title(u'ゴールド価格(円換算時)の変化量の分布',fontproperties=fp)

ヒストグラムの中で、青色が実際のゴールド価格(円換算)の分布、緑色が正規分布の乱数で再現した分布です。
視覚的には正規分布に近いように思われます。
厳密には、統計的検定処理(※)を用いて正規分布と見てよいかどうか定量的にチェックするのですが、
ここでは解説を分かりやすくするため、正規分布と仮定して話を進めていきます。

それでは、ドル円とゴールドで構成される資産ポートフォリオのリスクについて、モンテカルロシミュレーションをして求めたいと思います。
プロフィットファクターとなるドル円、ゴールドのいずれも正規分布に従って振舞うと仮定します。
ドル円とゴールド価格(円換算)の統計情報は以下のとおりです。

print "[ドル円の統計情報]"
avg_usdjpy = pf_history['diff_usdjpy'].mean()
std_usdjpy = pf_history['diff_usdjpy'].std()
print "平均値:%s    標準偏差:%s" % (avg_usdjpy,std_usdjpy)

print "[ゴールド(円換算)の統計情報]"
avg_goldjpy = pf_history['diff_gold_jpy'].mean()
std_goldjpy = pf_history['diff_gold_jpy'].std()
print "平均値:%s    標準偏差:%s" % (avg_goldjpy,std_goldjpy)


# 実行結果
[ドル円の統計情報]
平均値:-0.000821705426357    標準偏差:0.621896383698

[ゴールド価格(円換算)の統計情報]
平均値:-53.1459224806    標準偏差:1203.38599955

それでは、時系列データの最初のレコードにあるドル円とゴールド価格(円換算)の値を初期値として、
モンテカルロシミュレーションを実施します。

ドル円とゴールド価格(円換算)の初期値は次のようになります。

# 最初の日の相場を取り出す
first_index = df_usdjpy.index[0]

first_usdjpy = df_usdjpy.ix[first_index]
first_gold = df_gold.ix[first_index]

# 保有資産はそれぞれ100億円分でスタート
start_value = 100 * 100000000

# 初日の終値から購入量を計算する
# 100億円 ÷ 終値 = 資産購入量
amount_usd  = start_value * 1.0 / first_usdjpy['close']
amount_gold = start_value * 1.0 / ( first_gold['close'] * first_usdjpy['close'] )

first_value_usdjpy = first_usdjpy['close']
first_value_goldjpy = first_gold['close'] * first_usdjpy['close']

print "[ドル円初期値] %s" % (first_value_usdjpy)
print "[ゴールド価格(円換算)初期値] %s" % (first_value_goldjpy)
print "ドル購入量(100億円分) = %s ドル" % (amount_usd)
print "ゴールド購入量(100億円分) = %s オンス" % (amount_gold)

# 実行結果
[ドル円初期値] 120.419
[ゴールド価格(円換算)初期値] 141131.068
ドル購入量(100億円分) = 83043373.554 ドル
ゴールド購入量(100億円分) = 70856.1207799 オンス

それでは正規分布に基づいてドル円とゴールド価格それぞれをシミュレーションしていきましょう。
CSVファイルから読み込んだドル円のヒストリカルデータの日数だけ、各シミュレーションで再現します。
ここでは、ドル円・ゴールド価格それぞれを独立した値として正規分布乱数で再現しています。

モンテカルロシミュレーションで計算して得られたポートフォリオ価値の変化量が、df_mc_historyにセットされます。

# モンテカルロシミュレーションで求めたポートフォリオ価格の推移を記録する
mc_pf_history = []

# シミュレーション回数
simulate_count = 1000
for sim_count in range(simulate_count):
    
    # 各シミュレーションごとのパラメータ初期化
    value_usdjpy = first_value_usdjpy
    value_goldjpy = first_value_goldjpy
    pf_value_last  = start_value * 2    
    for pos in range(len(df_usdjpy.index)):
        pf_value = value_usdjpy * amount_usd + value_goldjpy * amount_gold
        diff_pf_value = pf_value - pf_value_last
        mc_pf_history.append(diff_pf_value)
        pf_value_last = pf_value 
        #print "[portfolio value] %s" % (pf_value)
        value_usdjpy += normal(avg_usdjpy,std_usdjpy)
        value_goldjpy += normal(avg_goldjpy,std_goldjpy)

# データフレームを作成する
df_mc_history = pd.DataFrame(mc_pf_history,columns=["diff_pf_value"])

その内容は以下のようになっています。

print df_mc_history.sort(["diff_pf_value"])

[実行結果]
diff_pf_value
79      -4.432048e+08
227754  -4.421918e+08
167223  -4.302939e+08
198247  -4.170626e+08
163335  -4.161237e+08
146909  -4.159292e+08
・・・中略・・・
126449   4.157391e+08
195380   4.185602e+08
83652    4.200358e+08
16868    4.235123e+08

[259000 rows x 1 columns]

そして、標準偏差とValue at Riskの値は次のようになります。

print "[標準偏差:モンテカルロシミュレーション法]\n %s" % (df_mc_history["diff_pf_value"].std())
print "[平均値:モンテカルロシミュレーション法]\n %s" % (df_mc_history["diff_pf_value"].mean())
print "[Value at Risk:モンテカルロシミュレーション法]\n %s" % (df_mc_history["diff_pf_value"].std()*2.33)

# 実行結果
[標準偏差:モンテカルロシミュレーション法]
 99621110.9981
[平均値:モンテカルロシミュレーション法]
 -3711422.06767
[Value at Risk:モンテカルロシミュレーション法]
 232117188.625

得られたValue at Riskは、232,117,188(円)です。
ドル資産とゴールド資産のそれぞれのValue at Riskを足し合わせて求めた 319,002,206(円)より小さい値になっています。
ポートフォリオ効果が現れているように見えます。

それはなぜでしょうか？

鍵を握るのは、リスクファクター間の相関性です。

一般的に、リスクファクター間の相関が小さいほど（相関係数が-1に近いほど）、
ポートフォリオ効果が強くなり、リスクが小さくなります。
すなわち、ポートフォリオの資産価値の変動が抑えられ、安定した動きを示すようになります。

逆に、リスクファクター間の相関が強いほど、ポートフォリオ効果が弱くなり、
ポートフォリオの資産価値が大きく変動するようになるのです。

先ほどのモンテカルロシミュレーションでは、ドル円とゴールド価格をそれぞれ独立に再現していました。
つまり、お互いの値動きが無関係というわけです。
このとき、相関係数は０に近づきます。
実際に計算して確かめてみましょう。

# モンテカルロシミュレーションで再現したリスクファクターの値（ドル円＆ゴールド価格）の相関を調べる
df_mc_factor = pd.DataFrame(columns=["usdjpy","goldjpy"])

# シミュレーション回数
simulate_count = 1000

factor_usdjpy = []
factor_goldjpy = []
for sim_count in range(simulate_count):
    # 各シミュレーションごとのパラメータ初期化
    value_usdjpy = first_value_usdjpy
    value_goldjpy = first_value_goldjpy
    for pos in range(len(df_usdjpy.index)):
        # 通常配列に追加するほうが、データフレームとして追加するよりずっと速い
        factor_usdjpy.append(value_usdjpy)
        factor_goldjpy.append(value_goldjpy)
        value_usdjpy += normal(avg_usdjpy,std_usdjpy)
        value_goldjpy += normal(avg_goldjpy,std_goldjpy)

df_mc_factor['usdjpy'] = factor_usdjpy
df_mc_factor['goldjpy'] = factor_goldjpy

ドル円とゴールド価格を格納したデータフレーム df_mc_factorの内容は以下のようになっています。

print df_mc_factor


# 実行結果
  usdjpy        goldjpy
0       120.419000  141131.068000
1       119.822150  142183.719098
2       120.210256  140618.852137
3       121.115134  139394.454146
・・・中略・・・
258996  106.619950  120098.009049
258997  106.963162  119254.657631
258998  107.150401  121683.794572
258999  107.319467  122637.735465

[259000 rows x 2 columns]

それでは相関係数を見てみましょう。

print df_mc_factor.corr()

# 実行結果
            usdjpy   goldjpy
usdjpy    1.000000  -0.018069
goldjpy  -0.018069  1.000000

usdjpyどうし、goldjpyどうしの相関係数は1.0になっている一方、
usdjpyとgoldjpyの相関係数は -0.018069 と小さい値になっています。
ポートフォリオ効果がはっきりと現れる状態ということがわかります。

【さらに学習を深めるには】

より詳細なシミュレーションを実施するためには、ドル円とゴールド価格の間の相関関係をシミュレーションする必要があります。
実際の相場の値動きから相関係数を求め、その相関係数に準じた対応関係を示すように、ドル円とゴールド価格を再現する処理を実装するわけです。
相関を持つ複数の乱数を生成するには、コレスキー分解という数学的アプローチを用いた方法があります。

このブログエントリーの内容をベースにして、あなた自身の手でコードを実装してみましょう！

参考：
http://qiita.com/horiem/items/e3dfe0a0f0ac3a66f509

*.参考資料

日銀のValue At Risk の解説がとても分かりやすく、参考になります。
ぜひ一読してみましょう。
https://www.boj.or.jp/announcements/release_2015/data/rel150929a2.pdf

*.配布データ

【ダウンロード(Jupyter Notebook)】blog-2017-1Q-fintech-value-at-risk-release
【データダウンロード】usdjpy_2001_2017
【データダウンロード】xau_usd_2001_2017

 最後に

次世代システム研究室では、機械学習や統計処理に関心を持つ開発者、アーキテクト、データサイエンティストを求めています。

自由闊達にのびのびと働きながら学べる環境が、コーヒー片手にアカデミックとビジネスの融合したディスカッションをしながら、知的好奇心を満たすことができる環境があなたを待っています。

次世代システム研究室にご興味を持たれたらすぐに 募集職種一覧 からご応募してください。

皆さんのご応募をお待ちしています。