金融時系列予測におけるクロスバリデーション手法

概要

• 金融時系列データではラベル情報のリークや過学習を防ぐため、Walk-Forward法、Purged K-Fold、CPCV、Adaptive/Bagged CPCVなど専用のクロスバリデーション手法が必要不可欠です。
• CPCVとその派生形は、複数経路での評価や市場適応性により高い堅牢性を示しますが、計算コストとのトレードオフが存在します。
• バックテストの信頼性を客観的に評価するために、PBO（Probability of Backtest Overfitting）やDSR（Deflated Sharpe Ratio）といった指標の活用が重要です。

はじめに：なぜ金融時系列のCVは難しいのか？

こんにちは。グループ研究開発本部・AI研究開発室のR.I.です。

機械学習モデルで市場を予測してトレードで大儲け、機械学習エンジニアなら誰もが思い描いたことのある夢だと思います。しかし、単に予測精度が高いモデルを作るだけでは、その夢を実現するには不十分です。金融市場における予測モデル開発では、モデルの予測精度そのものだけでなく、「構築したモデルが未知の市場環境でも安定して機能するか」という堅牢性が極めて重要です。この堅牢性を測るために行われるのがバックテスト、すなわち過去データを用いた性能評価です。しかし、金融時系列データを用いたバックテストは、一般的な機械学習タスクにおける性能評価とは異なる難しさを含んでいます。

株価や為替レートなどの金融時系列データは、多くの場合、機械学習の基本的な前提である「独立同分布（IID; Independent and Identically Distributed）」を満たしません。データ点間に自己相関があったり、ボラティリティ（変動率）が時期によって大きく異なったり（ボラティリティ・クラスタリング）、市場の構造自体が変化したり（レジーム・シフト）します。

このような特性を持つデータに対して、画像認識などで用いられる通常の K-Fold クロスバリデーションを単純に適用すると、未来情報の漏洩（Leakage, リーケージ）が発生するリスクがあります。リーケージとは、本来知り得ないはずの未来の情報が訓練データに混入し、モデルが見かけ上高い性能を示してしまう現象です。これにより、バックテストの結果を過信してしまい、実際の運用で大きな損失を被る可能性があります。このような、「バックテストの結果は非常に良好だが、実運用では取引戦略が機能しない」現象をバックテストの過学習（Backtest Overfitting）と呼びます。

本記事では、こうした金融データ特有の問題に対処するために考案された、時系列に特化したクロスバリデーション手法の進化と、バックテストの過学習を検出するための指標について解説します。

時系列特化CVの必要性：金融データの特性

金融時系列データを扱う際に通常のK-Foldクロスバリデーションでは不十分となる理由は、主に以下のような相関構造や非定常性を考慮する必要があるためです。

1. 自己相関: 金融市場では、トレンドやモメンタムなど、過去の値動きが未来の値動きに影響を与えるケースが少なくありません。ランダムにデータを分割すると時間的な順序が崩れてしまい、この相関構造を無視したままモデルを訓練することになります。
2. 情報の重複: 例えば「過去20日間のリターン」をもとにラベルを付与する場合、ある時点のラベルづけで利用した情報が、別の時点のラベルづけにも含まれることがあります。これが訓練データとテストデータ間で重複を起こし、未来情報のリーケージを引き起こす原因になります。
3. 非定常性（レジームシフト）: 金融市場は強気相場・弱気相場などの異なる「レジーム（局面）」を取りうるため、時間の経過に従ってデータの分布（平均や分散など）が変わることがしばしばあります。ある時期に学習したパターンが、後の時期でも同じように通用するとは限りません。

こうした要因から、時間的な順序を維持しつつリーケージを極力抑えた評価を行うために、通常のK-Foldとは異なる時系列特化のクロスバリデーション手法が必要となります。

基本的手法：ウォークフォワード法（Walk-Forward）

最も直感的で、データの時間的な順序を守る基本的な手法がウォークフォワード（WF）法です。ウォークフォワード法では、時系列に沿って複数の期間に分割したデータを用いて、最初の期間（訓練データ）でモデルを学習し、その直後の期間（検証データ）で性能を評価します。次に、訓練データ期間を一つ未来にスライドまたは拡張し、同様に学習と評価を繰り返します。

利点:

• 時間的な順序を完全に保つため、リーケージのリスクが非常に低い。
• 実際の取引や運用プロセス（過去のデータで学習し、未来を予測する）に非常に近い形で検証できる。
• 実装が比較的容易。

欠点:

• 評価経路が一つしかないため、結果が特定の期間の市場状況に強く依存し、評価の頑健性に欠ける。
• 訓練データを拡張していく実装では検証の初期段階における訓練データ量が少なく、モデルの学習が不安定になることがある。
• データ全体のうち、評価に使える部分が後半に偏る。

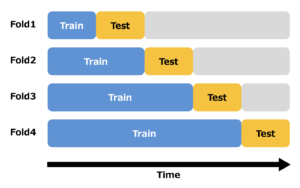
リーケージへの対策：Purged K-Fold CV

ウォークフォワード法は時間的な順序を守る点で自然ですが、データの利用効率が低く、検証データがデータの後半に偏るといった問題がありました。
そこで、通常の K-Fold CV を時系列向けに改良したのが Purged K-Fold CV です。

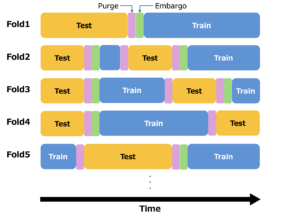
通常の K-Fold CV と同様に、データを K 個の連続したブロック（Fold）に分割します。各イテレーションで、一つのブロックをテストデータとし、残りを訓練データとします。ただし、金融データ特有のリーケージを防ぐために、以下の2つの処理を追加します。

1. パージ（Purging）: 検証データブロックの前後一定期間の訓練データを除去します。これにより、検証データの情報が訓練データに漏れるのを防ぎます。
2. エンバーゴ（Embargoing）: 各検証データブロックの直後に、パージ期間に加えて更に学習に使用しない期間を設けます。検証期間以降の情報は検証時に未来情報となるので、この期間を長く取り除くことで、訓練データと検証データの相関をより強く抑制することができます。

利点:

• 通常の K-Fold CV と同様に、検証データ以外のデータを訓練に利用できる。
• パージとエンバーゴにより、リーケージのリスクを低減する。

欠点:

• バックテストパス（期間全体に対するバックテストを行える経路）が1つしか無い。
• パージやエンバーゴの期間設定が適切でないと、リーケージが残る、あるいは有用なデータを過剰に除去してしまう可能性がある。

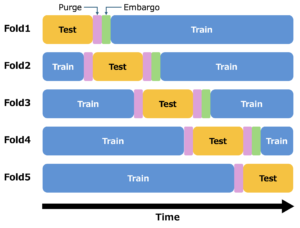
網羅性と堅牢性の追求：Combinatorial Purged CV (CPCV)

Purged K-Fold CV はデータ効率性とリーク対策を実現しましたが、評価の頑健性という点ではまだ改善の余地があります。そこで、検証期間を複数に増やし、より多くの組み合わせで評価を行うことでバックテストの過学習リスクをさらに低減するために提案されたのが Combinatorial Purged Cross-Validation (CPCV) です。

1. データを時系列に沿って N 個の連続したブロックに分割します。
2. N 個のブロックの中から、テスト用として k 個のブロック (k < N/2) を選択する全ての組み合わせを考えます。組み合わせの総数は _NC_k 通りです。
3. 各組み合わせについて、選択された k 個のブロックをテストデータとし、残りの N-k 個のブロックを訓練データとします。
4. 訓練データとテストデータの間で、Purged K-Fold CV と同様にパージ処理とエンバーゴ処理を適用します。
5. 全ての組み合わせについて評価を行い、結果を集計します。

利点:

• テストデータの組み合わせを網羅的に評価するため、特定の期間への依存度が低く、評価の頑健性が非常に高い。
• 多数のバックテストパスを生成することで、シャープレシオの分散を評価することができる（後述のPBO評価にも繋がる）。

欠点:

• ブロック数 N が大きくなると、テストブロックの組み合わせ数 (_NC_k) が爆発的に増加し、計算コストが非常に高くなる。

CPCVの進化：Bagged / Adaptive CPCV

CPCV は堅牢な評価手法ですが、計算コストの問題や、さらなる性能安定化への要求から、いくつかの拡張手法が研究されています。ここでは、 Bagged CPCV と Adaptive CPCV と呼ばれる2つの手法（Arian et al., 2024）を紹介します。

• Bagged CPCV: CPCV で生成される多数のバックテストパス（あるいはその部分集合）の結果を集約（バギング、特に平均化）するアプローチです。個々のパスの評価結果のばらつきを抑え、より安定した性能評価値を得ることを目指します。研究によれば、Bagged CPCV は DSR（後述）を改善する傾向がある一方で、PBO（後述）は若干悪化する可能性も示唆されています。これは、バギングによって個々の（過学習した可能性のある）パスの特徴が平均化され、過学習の兆候が見えにくくなるためと考えられます。
• Adaptive CPCV: 市場の状況に応じて CPCV のブロック分割方法や組み合わせの選び方を動的に変更するアプローチです。例えば、市場のボラティリティが高い時期と低い時期でテストブロックの期間や数を変えたり、特定のレジームに合った組み合わせを重視したりします。これにより、市場環境の変化により柔軟に対応した、より現実的なバックテストを構築することを目的としています。論文中では、ボラティリティに基づいて分割を調整する Adaptive CPCV が、テストされた手法の中で最も低い PBO と最も高い DSR を達成したと報告されており、その有効性が示されています。

これらの拡張手法は、CPCV の堅牢性をベースに、特定の目的（安定性向上、市場適応性向上）に合わせて改良を加えたものであり、実用化に向けた研究が進んでいます。

バックテストの過学習を測る：PBOとDSR

これまで見てきたように、洗練された CV 手法はバックテストの信頼性を高めますが、「どの程度過学習しているのか？」を定量的に評価する指標も重要です。特に以下の二つが広く知られています。

• PBO (Probability of Backtest Overfitting):
  CPCV のように多数のバックテストパスを評価した際に、「最も性能が良かったパス（＝選択される戦略）が、他の多くのパスの中央値よりも性能が劣る確率」を計算します。言い換えれば、「最も良く見えた戦略が、実は偶然の産物（過学習）である確率」を示す指標です。PBO が 0.05 なら、最良戦略が過学習である可能性は 5% と解釈できます。一般的に、PBO が低いほど、バックテスト結果の信頼性は高いとされます。
• DSR (Deflated Sharpe Ratio):
  通常のシャープレシオは、単一の戦略のリスク調整後リターンを測る指標ですが、多数の戦略の中から最良のものを選んだ場合、そのシャープレシオは選択バイアスにより高く出る傾向があります。DSR は、試行した戦略の数や、それらのシャープレシオのばらつきを考慮して、選択バイアスを補正（下方修正）したシャープレシオです。多数の戦略を比較検討したという事実を考慮に入れることで、より現実的で保守的な性能評価を提供します。例えば、1000個の戦略を試して見つけたシャープレシオ2.0よりも、10個の戦略から見つけたシャープレシオ1.5の方が、DSRで評価すると信頼性が高い、といった判断が可能になります。

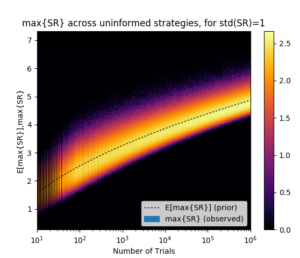
Bailey らが “The most important plot in finance” と呼んだ下の図は、試行回数（Number of Trials）が増えるほど見かけ上の最大シャープレシオ（Expected Maximum Sharpe Ratio）が高くなるが、それは選択バイアスによるものである、ということを示しています。このため、パラメータ探索などで複数回バックテストを行う際には通常のSRではなく、DSRで評価すべきであることが分かります。

これらの指標を CV 手法と組み合わせて用いることで、単に性能が良いだけでなく、「過学習しておらず、統計的に信頼できる」モデルや戦略を選択することが可能になります。

まとめ

金融時系列予測におけるモデル評価は、データの特性上、特別な配慮が必要です。単純な CV はデータリークのリスクが高く、バックテストにおける過学習を見逃す可能性があります。この課題に対処するため、ウォークフォワード法から始まり、Purged K-Fold CV、そして網羅性と堅牢性を高めた CPCV へと評価手法は進化してきました。さらに、Bagged CPCV や Adaptive CPCV といった拡張手法も登場し、安定性や市場適応性の向上が図られています。

現状では、CPCV がバックテストの堅牢性を評価する上で強力な基盤となりますが、計算コストが高いという課題もあります。そのため、要求される評価の厳密さや利用可能な計算資源に応じて、ウォークフォワード法や Purged K-Fold CV、あるいは CPCV の派生手法を適切に選択・組み合わせることが現実的です。

そして、どの CV 手法を用いるにしても、PBO や DSR といった過学習評価指標の併用が有用です。これらの指標は、バックテストの結果が単なる偶然や過学習によるものではないかを確かめるための客観的な基準となります。

さいごに

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。

参考資料