2022.04.08
データから因果関係を導く!〜ルービン?パール?全部のせ〜
こんにちは。次世代システム研究室のY. O.です。
過去数度にわたって、統計的因果推論やその派生テーマについてブログを書いてきました。
そこで改めて、統計的因果推論の全体像を体系立って知りたい、というのが今回のテーマです。
調査を終えて、ちょっと調べただけではその体系を知ることができないな、というのが正直な感想です。まとまりきっていない部分もありますが、前半に体系論、後半に実例を用意していますので、同じ悩みを抱えている方の少しでも助けになればと思います。
因果推論の全体像
そもそもなぜ因果推論なのか
“因果と相関は違う”、と統計学の基礎講義を受けた学生だけでなく、ビジネス界隈でも基礎知識として浸透してきている気がします。また、ビジネス×統計学(この領域をデータサイエンスと呼んだりしますが)、が非常にパワフルだと認められてきています。
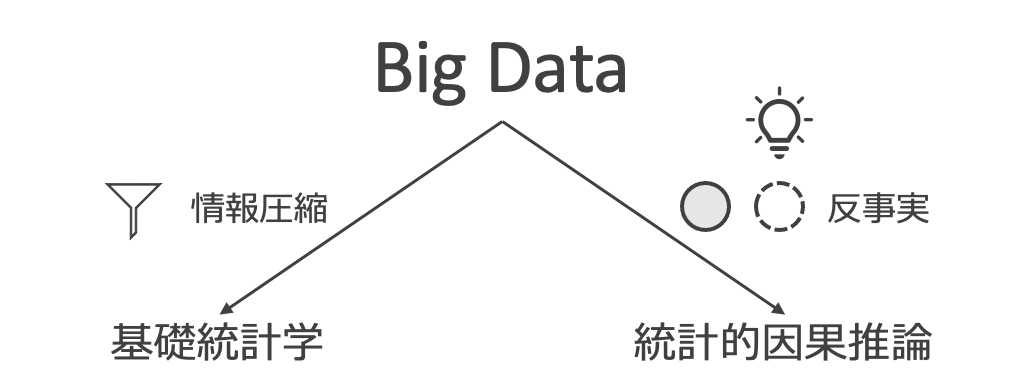
いま一度、基礎統計学では何を目的にしていたのかを振り返ってみましょう。“the object of statistical methods is the reduction of data” (R. A. Fisher, 1922)と、統計理論・情報理論に貢献したフィッシャーは述べており、引用の周囲とあわせて翻訳すると“データから、必要な情報・できれば情報の全てを集約・削減して表現すること、が統計学である”と言っています。
さて、ここで気がつくのは、基礎統計学では“因果”については全く触れていないということです。ですがビジネスシーンを思い浮かべてみると、基礎統計学の手法によりデータを集約表現した後は、なにかアクションを取りたくなり、そうなってくると、基礎統計学を拡張して、データに潜む“因果”を解析対象とする必要があります。
主な流派
少し調べると、統計的因果推論の枠組みとしては、Judea PearlとDonald Rubinの2つが主流ということがわかります。そして、Pearlは構造的因果モデル(SCM: Structual Causal Model)の枠組みによる因果推論手法であり、Rubinはポテンシャルアウトカムを用いた欠損値補完の枠組みによる因果推論手法だ、というような説明が各所でなされているように思えます。
ですが、今回調査をした限りにおいては、PearlはSCMに基づいた因果推論、RubinはSCMに基づかない因果推論、という程度の違いしか無いのではないか、という整理に至りました。
Pearlの因果推論
DAG
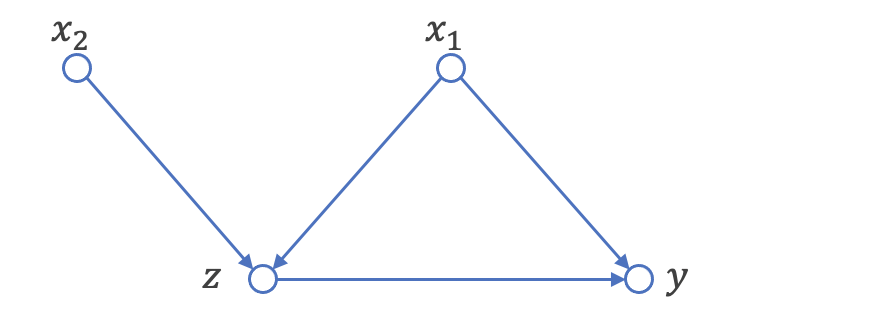
Pearlの因果推論は、有向非巡回グラフ(DAG: Directed Acyclic Graph)を主なパーツとしています。データにある因果の流れを記述したものがSCMであり、それをグラフ表現に直したものの一種がDAGとなります。
DAGのルールとしては、1. 変数間の因果方向が明らかになっている有向エッジがある・2. 変数の因果を辿ると自らの変数に戻ってくる自己フィードバックループが存在しない、の2つが挙げられます。
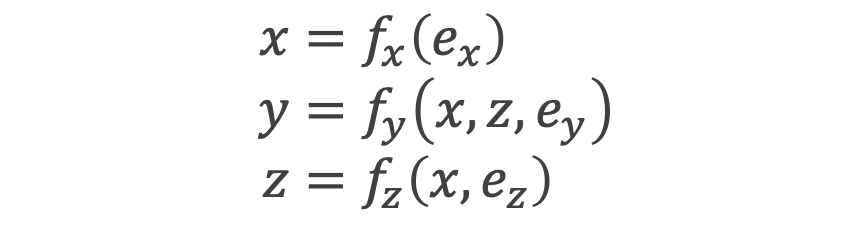
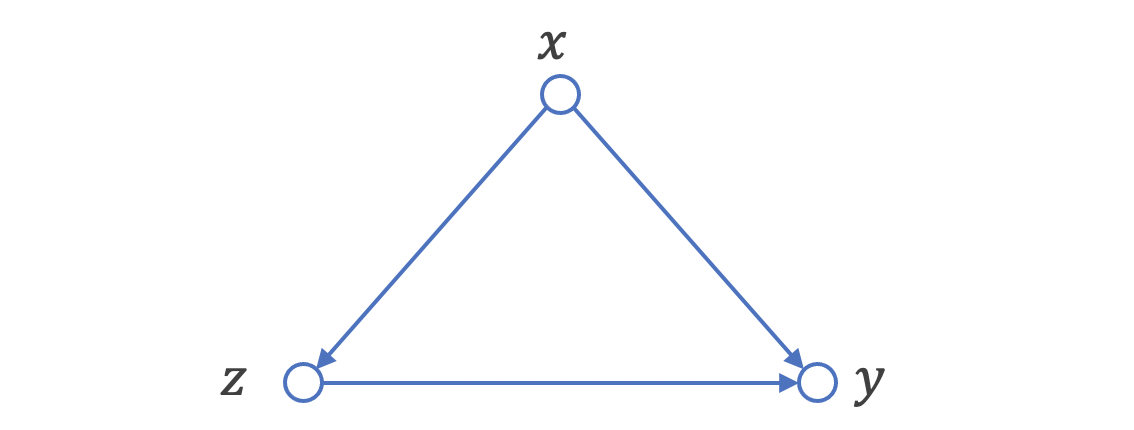
バックドア基準
上のDAGについてもう少し考察をしてみます。このDAGでは、変数ZからYに因果の向きがあることがわかっているのですが、Yについて、Zによる条件付き確率を因果効果として利用することはできません。あまりに有名な例ですが、ノーベル賞受賞(Y)と1人あたりのチョコレート消費量(Z)の間に正の相関関係がみられる、という現象も、このDAGに該当します(この例ではZ→Yのエッジは存在しないかもしれません)。
このような見せかけの因果(= 交絡)を生んでしまう変数Xは、バックドア基準、を満たす変数と定義されます。この状況を説明してみると、DAGの因果方向を考えるとZの変化により確かにYには変化が伝搬しますが、Zが変化したということはXが先に変化しているはずで、俯瞰するとXの変化が起点となってZ・Yが変化していると理解すべき、というイメージです。
この交絡が存在する限り、求めたい因果効果を手に入れることはできないのですが、Pearlはこのバックドア基準を満たす変数を固定(= d分離)してしまうという方法で、ZからYへの因果効果を見積もります。その結果が、調整化公式、となります。
調整化公式
交絡を取り除き、最終的な因果効果を見積もるステップに入ります。ここで新たにdoオペレータという概念を登場させますが、これは、自然にその値をとったのではなく介入した結果その値をとった、ことを示す表記となります。
doオペレータを交えながら、d分離した後のDAGを考えて式変形を行うと、以下の調整化公式が登場します。右辺分母は一般に傾向スコアと呼ばれていて、最終的に効果を見積もるフェーズでは、調整化公式自体がRubinのフレームワークでよく耳にするIPW推定量と全く同じ式に帰着していることがわかります。
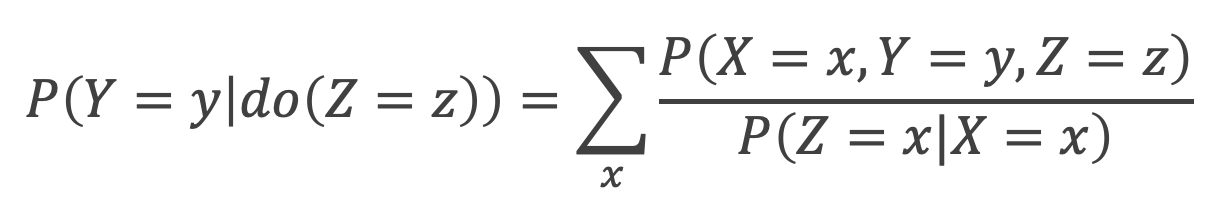
Rubinの因果推論
ポテンシャルアウトカム
Rubinはポテンシャルアウトカムに基づく因果推論フレームワークだ、というような説明がよくなされます(実はPearlはポテンシャルアウトカムを否定している訳ではありません。Pearlは“SCMの派生的性質として”ポテンシャルアウトカムを自然に定義できるとしています)(ポテンシャルアウトカムと同じ意味で、反事実やcounterfactualという単語が用いられることもあります)。ポテンシャルアウトカムとは、実際の結果とは反対の、実際には発生しておらず観測できていないが潜在的に起こり得た結果、を指します。この“観測できていない”というのがポイントで、機械学習の発展とともに、観測できていない値を機械学習を使ってより正確に求められないだろうかという学問領域に近年は拡張しています。また、“観測できていない”値の推定という枠組みから、Rubinの因果推論が欠損値補完の枠組みだと説明されることもあります。
傾向スコア
変数Zの割当は変数Xのみに依存していて、変数Yには依存していないとき、次式のように書き表すことができます(この変数の関係性はPearlの説で取り上げたDAGと同じです)。

この関係が成立するとき、変数Xは“強く無視できる割り当て”条件が成立していると呼ぶのですが、この条件下で、以下に定義される傾向スコアを条件付ければ、変数Zと変数Yを独立にすることができます。つまり、傾向スコアさえ手に入れることができれば、観測結果の中からポテンシャルアウトカムを探すことができるようになるのです。
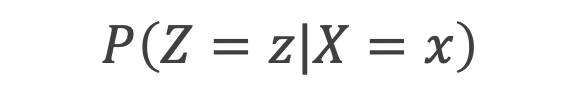
機械学習を利用する様々な手法
RubinはSCMに基づかないため、少しだけ自由にポテンシャルアウトカムを推定することができます。また前述のように、近年の機械学習の発展と相まって、このポテンシャルアウトカムを機械学習により正確に求めようと様々な手法が提案されています。ここからは、その手法たちを種類別に見ていくことにします。
重み付け
傾向スコアの逆重み付けを利用したIPW推定がこの区分に対応します。IPWだけに関して言えば、上述のPearlのフレームワークで登場した調整化公式の結果と等しくなります。
この区分はIPWだけでなく、IPWの欠点を補う形で拡張したDoubly Robust法や、IPWで用いる傾向スコアそのものの推定方法を改善したCovariate Balancing Propensity Score法が存在します。
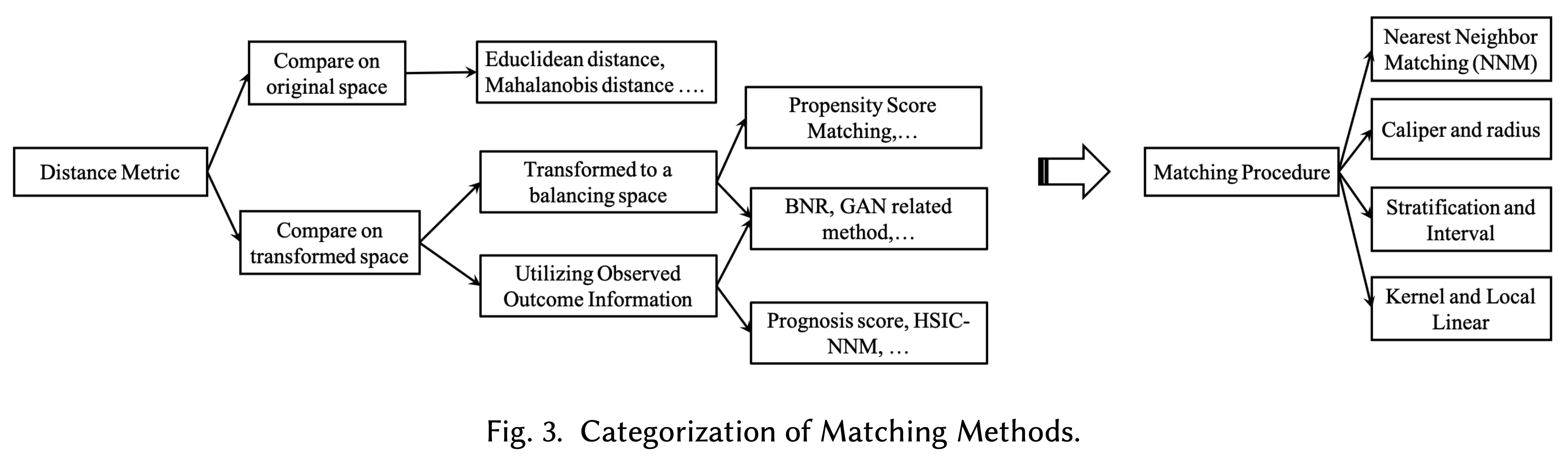
マッチング
同程度の傾向スコアを持つサンプルを反事実として利用し、観測値と反事実の差を因果効果の量とする方法です。“同程度”をどのように定義するかですが、KNNやKDEなどの統計手法が主に用いられます。
Meta-Learner
変数Xだけでなく変数Zもインプットとした機械学習モデルを作成し、その機械学習モデルが出力する反事実Yの値を利用することで、因果効果を見積もる方法です。この機械学習モデルについては基本的に非線形のモデルを想定しており、変数Zごとに別モデルを学習する方法などと合わせて様々な手法が提案されています。
表現学習
Rubinによる欠損値の枠組みを利用した問題設定をドメイン適応の問題と捉え直し、反事実をより正確に入手できるような特徴量表現を学習する手法になります。広く捉えると、上述した傾向スコアを利用した各種手法も、変数Zの割付を評価関数として変数Xを1次元表現に変換したものだと言うことができます。
介入群における平均処置効果を推定する方法
これまでは全サンプルに対して反事実を推定するための様々な手法を紹介しました。最後に、介入群における平均処置効果(ATT: Average Treatment effect on the Treated)を推定する方法を紹介します。
DID
差の差分析(DID: Difference in Difference)と呼ばれる手法です。DIDの分析を成立させるためには“平行トレンド仮定が成立していることが重要”と強調されることが多いですが、それだけではなく、この手法によって推定される効果はATTであるということも同様に重要な点です。手法の詳細は別ブログに記載していますので、そちらをご参照ください。
Causal Impact
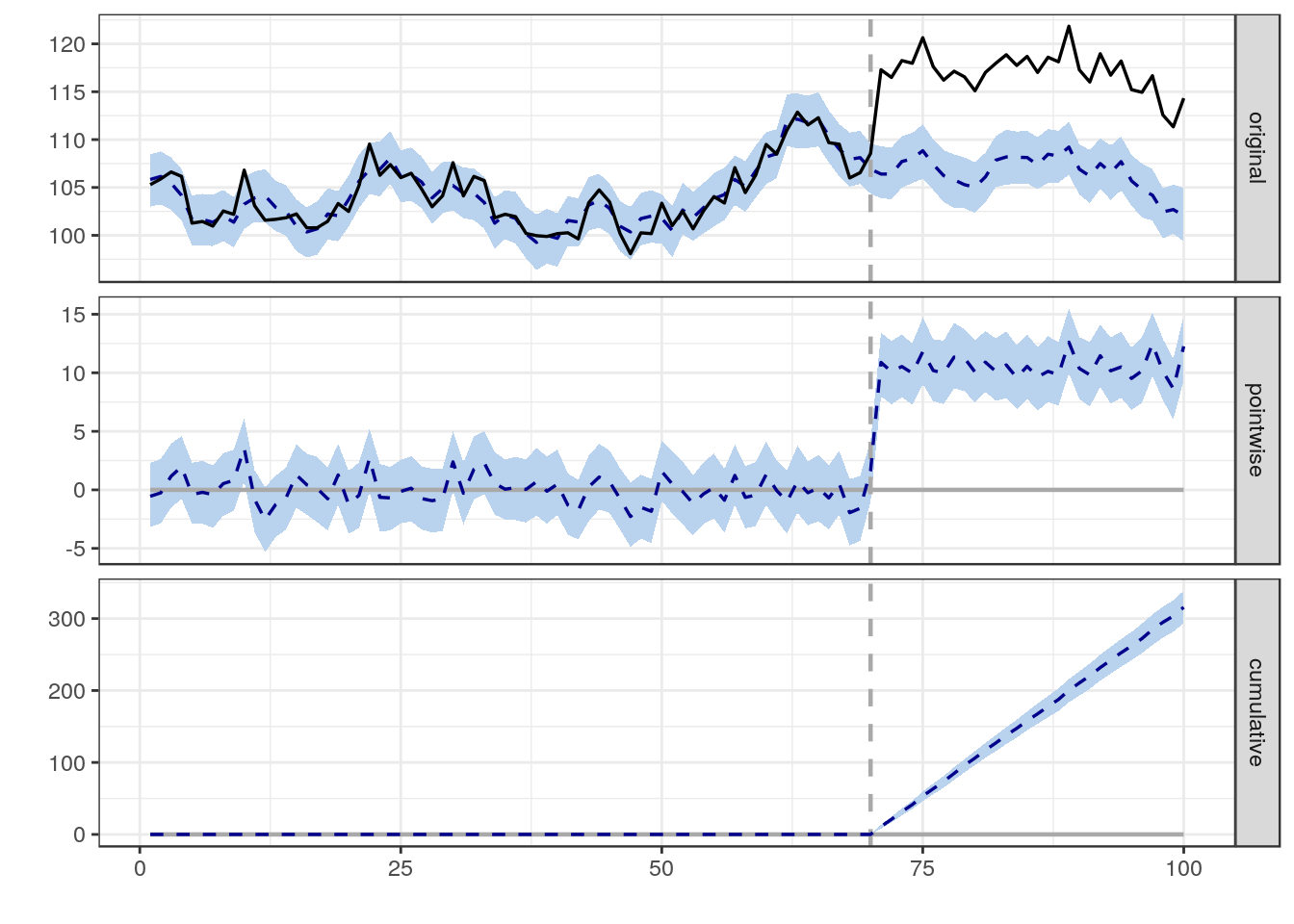
介入を受けていない対照群を利用しなくても因果効果の量を推定できる手法になります。過去期間での変数XとYの関係をモデリングし、介入後の期間で観測された変数Yと、モデルの出力結果との差分を因果効果として見積もります。ただし、この手法は介入Zが変数Xに変化を与えないという仮定が存在する部分が使いにくいです。対照群を利用しなくても良いという強みは消えてしまうのですが、過去期間データを利用して、対照群の変数Xから介入群のYを説明するモデルを学習するという方法とすれば、介入Zが変数Xに変化を与えないという仮定を排除することができます。時系列データを前提とした解析手法になるので、モデリングには状態空間モデルを利用するケースも多く見られます。
実データを用いたPearlとRubinの因果推論
上記で概要を一通り述べましたので、実際のデータを利用して簡単なデモをしてみようと思います。
データ作成
まずは今回のデモで利用するライブラリをインポートします。見かけないライブラリpgmpyは、Pearlの因果推論フレームワークにて、データからDAGを推定する際に利用します。
import numpy as np
import pandas as pd
from scipy.special import expit
import itertools
import warnings
warnings.simplefilter('ignore', FutureWarning)
from pgmpy.estimators import ConstraintBasedEstimator
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import auc, roc_curve
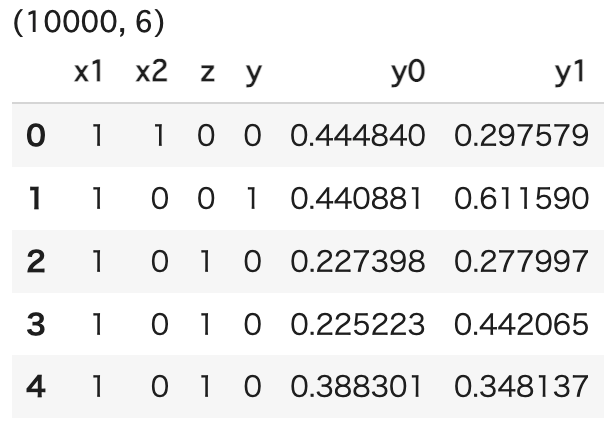
次に、データの生成です。以下のコードでは、x1, x2がzを生成し、x1, zがyを生成するようなデータを生成しています。また、データ生成のストーリーをDAGでも表現してみました。
class SampleDataset:
@classmethod
def generate_df(cls, num_data=10000, seed=0):
np.random.seed(seed=seed)
x1 = np.random.choice([0, 1], num_data, p=[0.3, 0.7])
x2 = np.random.choice([0, 1], num_data, p=[0.6, 0.4])
z = cls._get_logistic(num_data, [0.5, 1, -2], [1, x1, x2])
y = cls._get_logistic(num_data, [0.2, -1.5, 1], [1, x1, z], prob=False)
y0 = cls._get_logistic(num_data, [0.2, -1.5, 1], [1, x1, 0], prob=True)
y1 = cls._get_logistic(num_data, [0.2, -1.5, 1], [1, x1, 1], prob=True)
df = pd.DataFrame({
'x1': x1,
'x2': x2,
'z': z,
'y': y,
'y0': y0,
'y1': y1,
})
return df
def _get_logistic(num_data, b_list, x_list, prob=False):
e_z = np.random.randn(num_data)
res = 0
for b, x in zip(b_list, x_list):
res += b * x
res += e_z
z_prob = expit(res)
func = lambda x: np.random.choice([0, 1], 1, p=[1-x, x])
if prob:
return z_prob
else:
return np.vectorize(func)(z_prob)
df = SampleDataset().generate_df() print(df.shape) display(df.head())
Pearlの因果推論
PearlはSCMに基づいた因果推論のフレームワークでした。ここでは、データのみを用いて、DAGを推定することに挑戦します。
class DAGEstimator:
def __init__(self, df):
self.est = ConstraintBasedEstimator(df)
self.cols = df.columns
self.num_variable = len(self.cols)
self.chk_pair = 2
self.test_0 = {c: [] for c in self.cols}
def test_0_dependency(self):
print('='*10 + '\n0次の独立性検定\n' + '='*10)
for pair in list(itertools.combinations(range(self.num_variable), self.chk_pair)):
c1 = self.cols[pair[0]]
c2 = self.cols[pair[1]]
cond = []
result = self.est.test_conditional_independence(
c1, c2, cond,
method='chi_square',
tol=0.05
)
if not result:
self.test_0[c1].append(c2)
self.test_0[c2].append(c1)
self._print_result(c1, c2, cond, result)
def test_1_dependency(self):
print('='*10 + '\n1次の独立性検定\n' + '='*10)
for key, value in self.test_0.items():
if len(value)<=1:
continue
c1 = key
for i, v in enumerate(value):
c2 = v
for j in range(len(value)):
if i==j:
continue
else:
cond = [value[j]]
result = self.est.test_conditional_independence(
c1, c2, cond,
method='chi_square',
tol=0.05
)
self._print_result(c1, c2, cond, result)
def test_n_dependency(self, c1, c2, cond):
print('='*10 + '\n任意の独立性検定\n' + '='*10)
result = self.est.test_conditional_independence(
c1, c2, cond,
method='chi_square',
tol=0.05
)
self._print_result(c1, c2, cond, result)
def _print_result(self, c1, c2, cond, result):
print("{}\tvs\t{}\t| {}\t: {}".format(
c1, c2, ', '.join(cond),
'独立' if result else '関連'
))
dag = DAGEstimator(df[['x1', 'x2', 'z', 'y']])
簡単に解析用のクラスを用意して、まずは全変数間の組み合わせに対して、独立性の検定を行ってみます。
結果としては、x1-x2の組み合わせのみが独立と判定できたため、グラフ構造のうち点線のエッジが切り離せることがわかります。
dag.test_0_dependency()

dag.test_0_dependency()
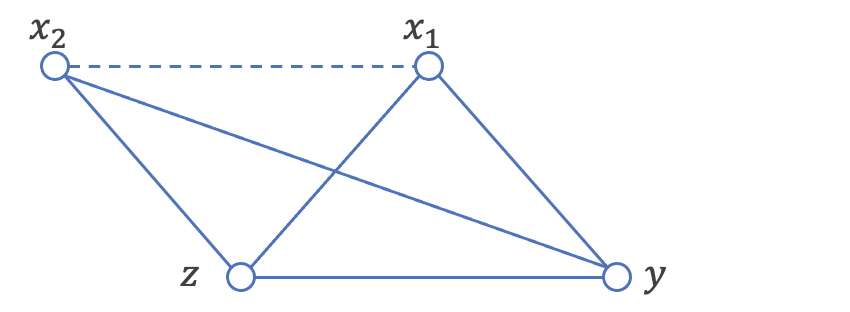
すると、zが条件に付いたときx2-yが独立となるので、x2-y間のエッジは切り離せることがわかります。
dag.test_1_dependency()

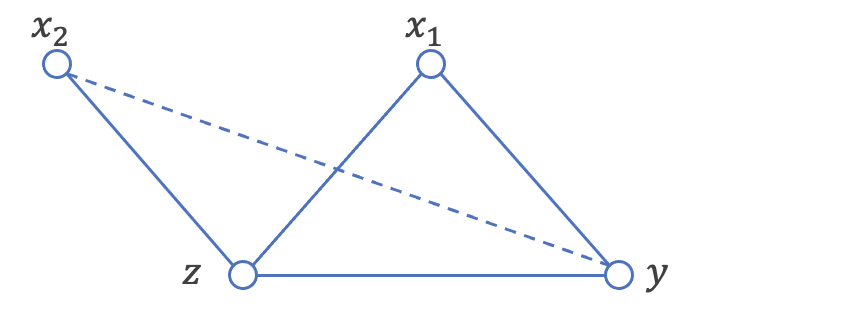
グラフにV字構造を持つとき、条件付き確率を計算することでエッジの向きを計算することができます。今回はx2-z-x1にV字構造が存在しており、zを条件につけてx2-x1間の独立性検定を行ってみましょう。
すると、zを条件につけると、実際にはエッジが存在しないx2-x1間に関連があるという結果になりました。これはグラフ理論で登場する、合流点の問題となり、x2, x1からzへの有向エッジを書くことができるようになります。
dag.test_n_dependency('x1', 'x2', ['z'])

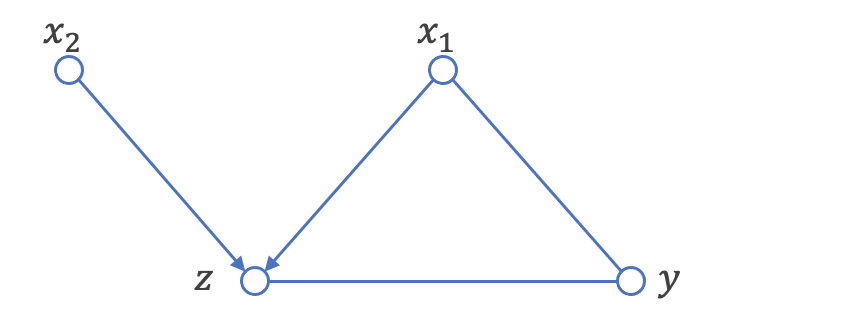
今回のデモの状況を考えると、「少なくとも効果yを知りたい状況なので、zからyにエッジの向きがあるだろう」「もしyからx1にエッジの向きがあると、巡回グラフとなってしまう」という2点を考慮して、最終的にはデータから正しいDAGを導くことになります。
この先の分析ストーリーとしては、先に登場した調整化公式を利用して介入効果(P(Y=y|do(Z=z)))を求めるわけなのですが、上述の通り、調整化公式自体がRubinの枠組みに登場するIPW推定と同じように定式化されるため、そちらに譲ることとします。
また、今回のDAG作成方法は、ベイジアンネットワークの手法を流用しています。ベイジアンネットワーク自体にも未観測のデータを推論する手法が存在します。
Rubinの因果推論
SCMには必ずしも基づくわけではないのがRubinの因果推論フレームワークでした。ここまでに生成したDAGは一旦忘れて、作成したデータセットからIPW推定を行ってみましょう。
class POEstimator:
def __init__(self, df):
self.df = df
self.df['z_0'] = 0
self.df['z_1'] = 1
def generate_prob_col(self, x: list, z: str, col: str, model=LogisticRegression()):
X = self.df[x]
y = self.df[z]
model.fit(X, y)
self.df[col] = model.predict_proba(X)[:, 1]
fpr, tpr, _ = roc_curve(y_true=y, y_score=self.df[col])
print('AUC ({})\t: {:.5f}'.format(col, auc(fpr, tpr)))
def get_true(self):
res = (self.df['y1'] - self.df['y0']).mean()
print('True causal effect\t: {:.5f}'.format(res))
def get_ipw(self):
res = self.df.apply(lambda x: self._calc_ipw(x), axis=1).mean()
print('IPW estimation\t: {:.5f}'.format(res))
def get_dr(self):
res = self.df.apply(lambda x: self._calc_dr(x), axis=1).mean()
print('DR estimation\t: {:.5f}'.format(res))
def _calc_ipw(self, x):
def _estimator(y, p_z, z):
return y / p_z * z
y1_hat = _estimator(x['y'], x['prob_z'], x['z'])
y0_hat = _estimator(x['y'], (1 - x['prob_z']), (1 - x['z']))
return y1_hat - y0_hat
def _calc_dr(self, x):
def _estimator(y, p_z, z, y_hat):
return (y / p_z) * z + (1 - z / p_z) * y_hat
y1_hat = _estimator(x['y'], x['prob_z'], x['z'], x['y1_hat'])
y0_hat = _estimator(x['y'], (1 - x['prob_z']), (1 - x['z']), x['y0_hat'])
return y1_hat - y0_hat
po = POEstimator(df)
先程作成したデータフレームを与えることで各種推定が実施できるようなクラスを準備して、いざ、IPW推定です。
po.generate_prob_col(['x1', 'x2'], 'z', 'prob_z') po.get_true() po.get_ipw()

結果を見てみると、真の効果量とおおよそ同じ値が推定できていることがわかります。
さて、次にDR推定量を求めてみましょう。Rubinのフレームワークでは特段SCMを意識しないため、以下のようにyのモデリングにx2を追加してしまうかもしれません。
po.generate_prob_col(['x1', 'x2', 'z_0'], 'y', 'y0_hat') po.generate_prob_col(['x1', 'x2', 'z_1'], 'y', 'y1_hat') po.get_true() po.get_dr()

モデリングには不要な変数x2を追加してしまっていますが、推定結果には特段影響がなさそうにみえます。これが中間変数のような変数だった場合、効果を過小見積もりしてしまうケースがありますが、今回はそのような結果は確認できませんでした。
Rubinの特徴として、SCMに基づくポテンシャルアウトカムに特段とらわれていないというように述べました。ここが、調整化公式だけでなく、種々の機械学習手法を導入できるポイントにもなります。
例えば、yの推定にランダムフォレストを用いることもできます。
po.generate_prob_col(['x1', 'z_0'], 'y', 'y0_hat', RandomForestClassifier()) po.generate_prob_col(['x1', 'z_1'], 'y', 'y1_hat', RandomForestClassifier()) po.get_true() po.get_dr()

最後に
統計的因果推論の体系を知りたいというモチベーションから調査を開始しましたが、調べれば調べるほど「先人たちよ、もう少し実務者にわかりやすく手法を一覧化しておくれよ」という気持ちが溢れてきました。学問体系として複数の流派が存在することは素晴らしいことですが、お互いに交通整理をして、統計的因果推論がよりビジネスに浸透していくことを期待しています。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。
一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
参考資料
[1] A Survey on Causal Inference (L. Yao, et. al., 2020)
[2] 入門 統計的因果推論(https://www.asakura.co.jp/detail.php?book_code=12241)
[3] 岩波データサイエンス Vol. 3(https://www.iwanami.co.jp/book/b243764.html)
[4] 調査観察データの統計科学(https://www.iwanami.co.jp/book/b257892.html)
[5] Inferring causal impact using Bayesian structural time-series models (Kay H. Brodersen, et. al., 2015) (https://google.github.io/CausalImpact/CausalImpact.html)
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD