2021.10.07
ビットコインの不正なトランザクションを見つける
目次
- 1. はじめに
- 2. トランザクションについて
2-1. トランザクションの特性
2-2. トランザクションとグラフ構造 - 3. トランザクションをクラスタリングする方法
3-1. GCNs
3-2. ARGVA - 4. 検証
4-1. データセット
4-2. 特徴量
4-3. 実装
4-4. 結果と考察 - 5. 最後に
TL;DR
Graph Convolutional Networks (GCNs) を用いてビットコインの不正なトランザクションを見つける。
- トランザクションをノード、支払いのフローをエッジとしてグラフを構築。
- GCNsを用いて、グラフの潜在ベクトルを取得し、T-SNEで可視化。
- k-Meansでクラスタリングすると意味のあるクラスタに分類できた。
1. はじめに
こんにちは、次世代システム研究室の新卒のK.Fです。今回で二回目の投稿になります。
ところで、皆さんはビットコインにはどのような印象をお持ちですか?2021年4月には一時、6万4000USD近くにまで価格が上昇し注目を集めました。ビットコインは暗号資産としての側面である投機目的だけではなく、ブロックチェーン技術を用いた新たな決済手段や金融取引の技術的革新をもたらしました。しかし、規制や法整備が十分に整っていないため、犯罪組織による資金洗浄(マネーロンダリング)に利用されているケースが発生しているようです。
ビットコインはその特性上、全ての取引情報(トランザクション)が公開されていますが、個人が複数のウォレット(銀行でいう口座)を持つことができるため、取引情報から個人を特定するのは困難です。C.Wさんの前回の投稿では、「GNNを使ってビットコインWalletを分類して可視化」し、ウォレットを意味のあるクラスタに分類する方法について説明されていました。今回は、C.Wさんの投稿とは異なる方法でグラフを構築し、ビットコインのトランザクションを意味のあるクラスタに分類できるか検証していこうと思います。意味のあるクラスタに分類し、不正なトランザクションを検知するのが目的です。
2. トランザクションについて
2-1. トランザクションの特性
以下の図はビットコインにおける取引(トランザクション)の流れです。
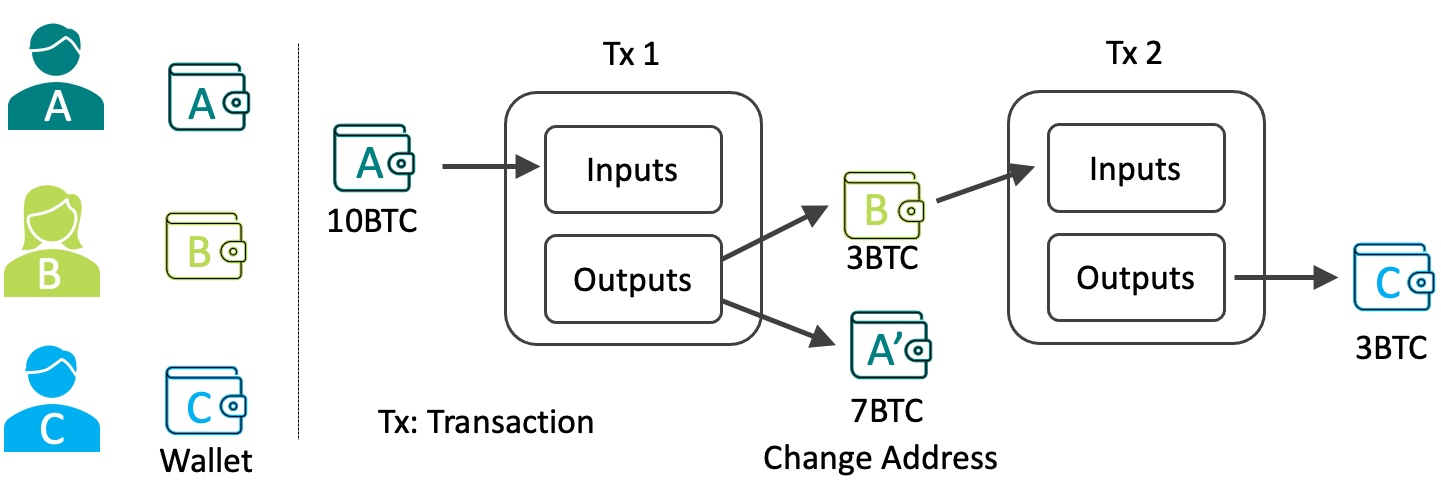
Aさんが未使用の出力10BTCを使用し、トランザクションの入力とします。AさんはBさんに3BTCを送金し、残りの7BTCを新しいアドレス(Change Addressと呼ばれます)に送金します。Bさんは未使用の出力を集めて、Cさんに送金するトランザクションを作成します。
このように、トランザクションは次から次のトランザクションに数珠繋ぎのように繋がっていきます。
2-2. トランザクションとグラフ構造
グラフとは、頂点(ノード)の集合とその間の連結関係を表す辺(エッジ)の集合で構成されるデータ構造のことです。
トランザクションの関係性をグラフ構造で表す方法は、二通りあります。
- アドレスをノード、トランザクションをエッジとする方法
このケースはC.Wさんが前回の投稿で検証されていた方法です。詳細は、リンク先をご覧ください。 - トランザクションをノード、支払いのフローをエッジとする方法
今回は、こちらに焦点をあてます。支払いのフローは向きが存在するので、有向グラフになります。
3. トランザクションをクラスタリングする方法
上記、2.の方法でトランザクションの関係性を表すグラフを構築し、グラフニューラルネットワーク(GNN)を用いて、トランザクションをクラスタごとに分類していきます。GNNは、ニューラルネットワークを用いてグラフの解釈を行う手法です。主に、グラフ分類、ノード分類、エッジ予測などの応用例があります。今回は、その中でもノード自体の性質を表すノード特徴量を扱うことができるGraph Convolutional Networks (GCNs) [1,2] を用います。
3-1. GCNs
GCNsは、その名の通りグラフ構造を畳み込む手法です。グラフ畳み込みでは、あるノードが持つノード特徴量を、隣接ノードが持つノード特徴量を加味して更新していきます。その作業(畳み込み)を繰り返すことでグラフ全体の特徴を捉えた特徴量になっていきます。GCNsへの入力は、各ノードの特徴行列とノードの接続関係を表した隣接行列で、出力は畳み込みで更新された各ノードの特徴行列です。
ここからは少し数式を追いかけて理解を深めていきます。ノードiにおけるl番目の中間層の特徴行列をh_i^(l)とするとl+1番目の特徴行列は以下のようになります。
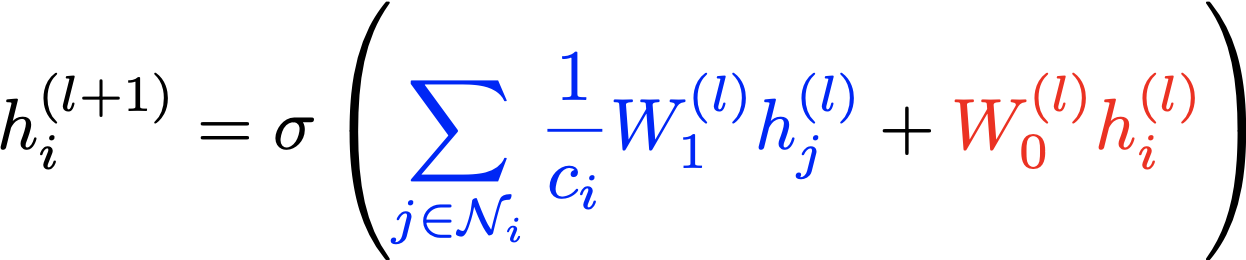
ここで、N_iはノードiの隣接ノードの集合、Wは重み、cは正規化項です。また、sigmaは活性化関数でReLU関数を用いるのが一般的です。
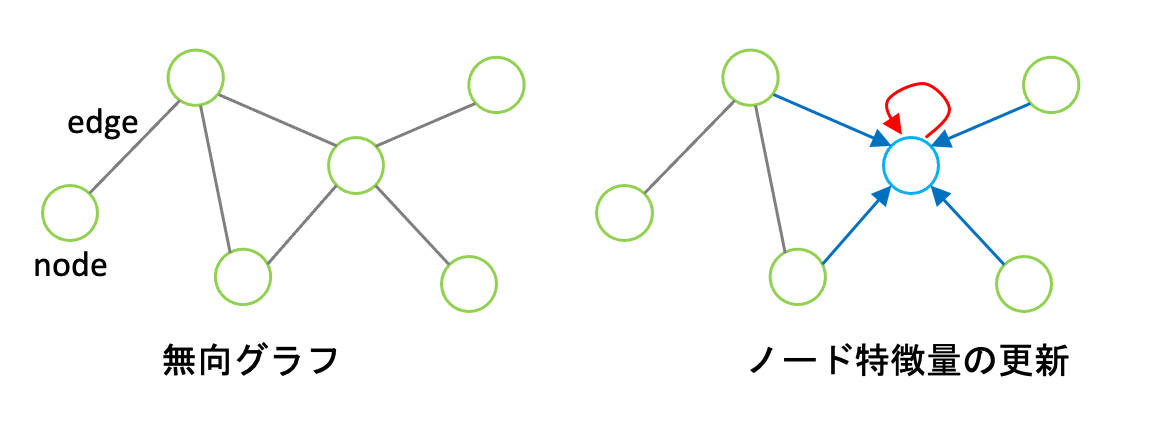
上式の青色で記述した項では、隣接ノードの特徴に重みをかけて足し合わせています(図の青色の矢印)。ここで、隣接ノードc_i=|N_i|で割って正規化していることも重要です。赤色で記述しているのが、自身の特徴を加味する項です(図の赤色の矢印)。
GCNsを用いて教師なしでグラフ構造からノードをクラスタリングする手法として、Adversarially Regularized Graph Variational Auto-Encoder (ARGVA) [3]があります。
3-2. ARGVA
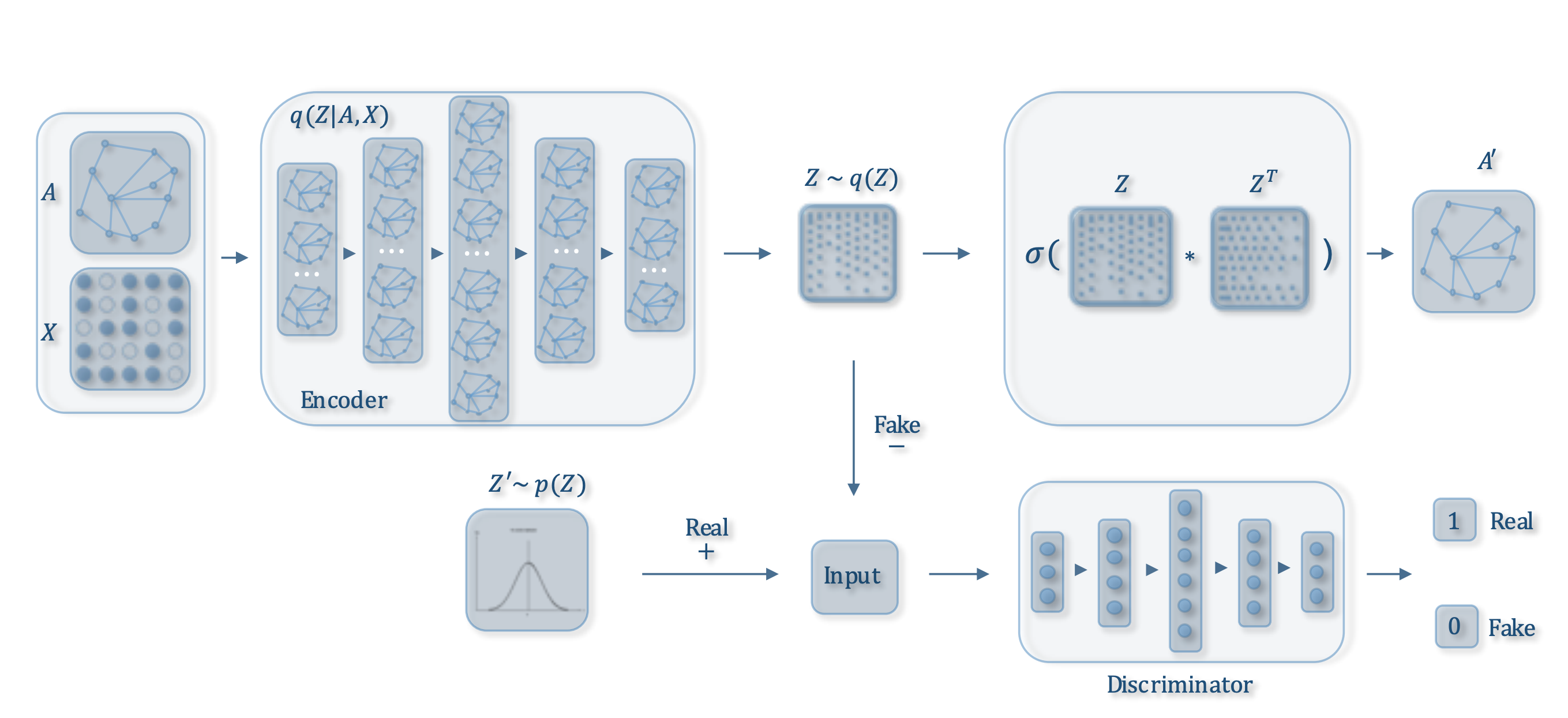
(図は論文から引用しています。)
隣接行列Aと特徴行列Xを潜在ベクトルZにencodeし、ZからA’をdecodeします。別に、Zの真贋判定を行う識別器を用意し、Zが事前分布からサンプルされたもの(真)か、encodeされたもの(贋)かを識別します。
真贋判定を行う識別器のbinary_cross_entropy誤差とAとA’のKL誤差を最小化することで学習を進めていきます。
4. 検証
4-1. データセット
ビットコイン・ブロックチェーンでは、全てのトランザクションの情報が公開されているので、実際のビットコイン・ネットワークからダウンロードしてくることが可能です。しかし、データを解析して整理するは大変、骨が折れる作業なので、今回は公開データセット[4]を用いました。といっても、トランザクションは一日に合計約20~40万個ほどブロックに書き込まれる(参考)ので、全てのトランザクションについて検証するのは不可能です。そのため、ビットコインが世界的に注目を集めはじめ、その当時の過去最高額である1万9800USDをつけた2017/12/17の00:00~23:59(UTC)の全トランザクションのデータを用いました。実際に検証に使用したデータのノード数は387781で、エッジ数は479689でした。
4-2. 特徴量
データセットから取得した特徴量と統計量を合わせて以下の表に示す10種類のノード特徴量を生成しました。
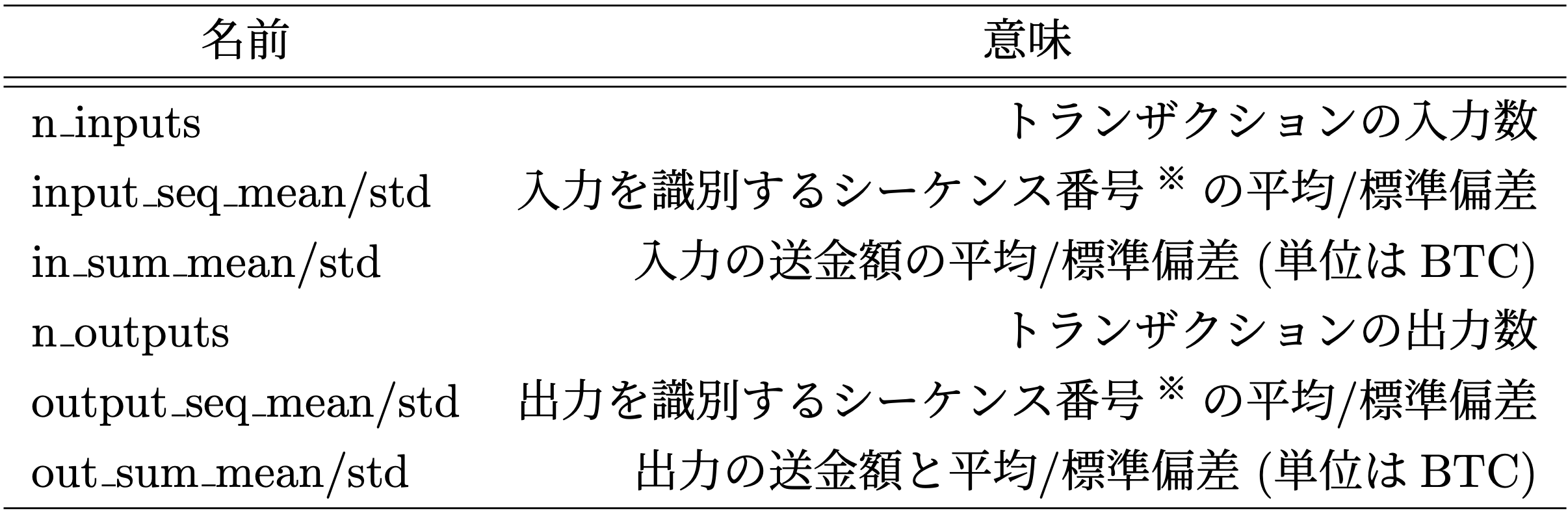
※ 入力(/出力)を識別するシーケンス番号とは、これまでに何回トランザクションの入力(/出力)として使われたかの回数
4-3. 実装
GCNsを使ったモデルはpytoch_geometricを用いることで簡単に実装することができます。こちらのExampleを参考にして実装しました。
import torch
from torch.nn import Linear
from torch_geometric.nn import GCNConv, ARGVA
class Encoder(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super().__init__()
self.conv1 = GCNConv(in_channels, hidden_channels)
self.conv_mu = GCNConv(hidden_channels, out_channels)
self.conv_logstd = GCNConv(hidden_channels, out_channels)
def forward(self, x, edge_index):
x = self.conv1(x, edge_index).relu()
return self.conv_mu(x, edge_index), self.conv_logstd(x, edge_index)
class Discriminator(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super().__init__()
self.lin1 = Linear(in_channels, hidden_channels)
self.lin2 = Linear(hidden_channels, hidden_channels)
self.lin3 = Linear(hidden_channels, out_channels)
def forward(self, x):
x = self.lin1(x).relu()
x = self.lin2(x).relu()
return self.lin3(x)
encoder = Encoder(n_features=10, hidden_channels=32, out_channels=32)
discriminator = Discriminator(in_channels=32, hidden_channels=64, out_channels=32)
model = ARGVA(encoder, discriminator).to(device)
encoder_optimizer = torch.optim.Adam(encoder.parameters(), lr=0.005)
discriminator_optimizer = torch.optim.Adam(discriminator.parameters(), lr=0.001)
# train
model.train()
n_epochs = 100
for epoch in range(n_epochs):
encoder_optimizer.zero_grad()
z = model.encode(train_data.x, train_data.edge_index)
for i in range(10):
discriminator_optimizer.zero_grad()
discriminator_loss = model.discriminator_loss(z)
discriminator_loss.backward()
discriminator_optimizer.step()
loss = model.recon_loss(z, train_data.edge_index)
loss = loss + model.reg_loss(z)
loss = loss + (1 / train_data.num_nodes) * model.kl_loss()
loss.backward()
encoder_optimizer.step()
# test
model.eval()
z = model.encode(data.x, data.edge_index)
z = z.cpu().numpy()
selected_idx = random.sample(list(range(z.shape[0])), 30000)
kmeans = KMeans(n_clusters=n_classes, random_state=seed).fit(z)
y = kmeans.predict(z)
z_selected = z[selected_idx]
z_selected = TSNE(n_components=2, random_state=seed).fit_transform(z_selected)
4-4. 結果と考察
潜在ベクトルをK-Meansで2クラスに分類した結果と潜在ベクトルをT-SNEで2次元に次元圧縮した結果を下図に示します。K-Meansの結果、クラスタ1には375740、クラスタ2には12041種類のトランザクションが分類されましたが、T-SNEで可視化しているのは3万点にランダムサンプルしたものです。
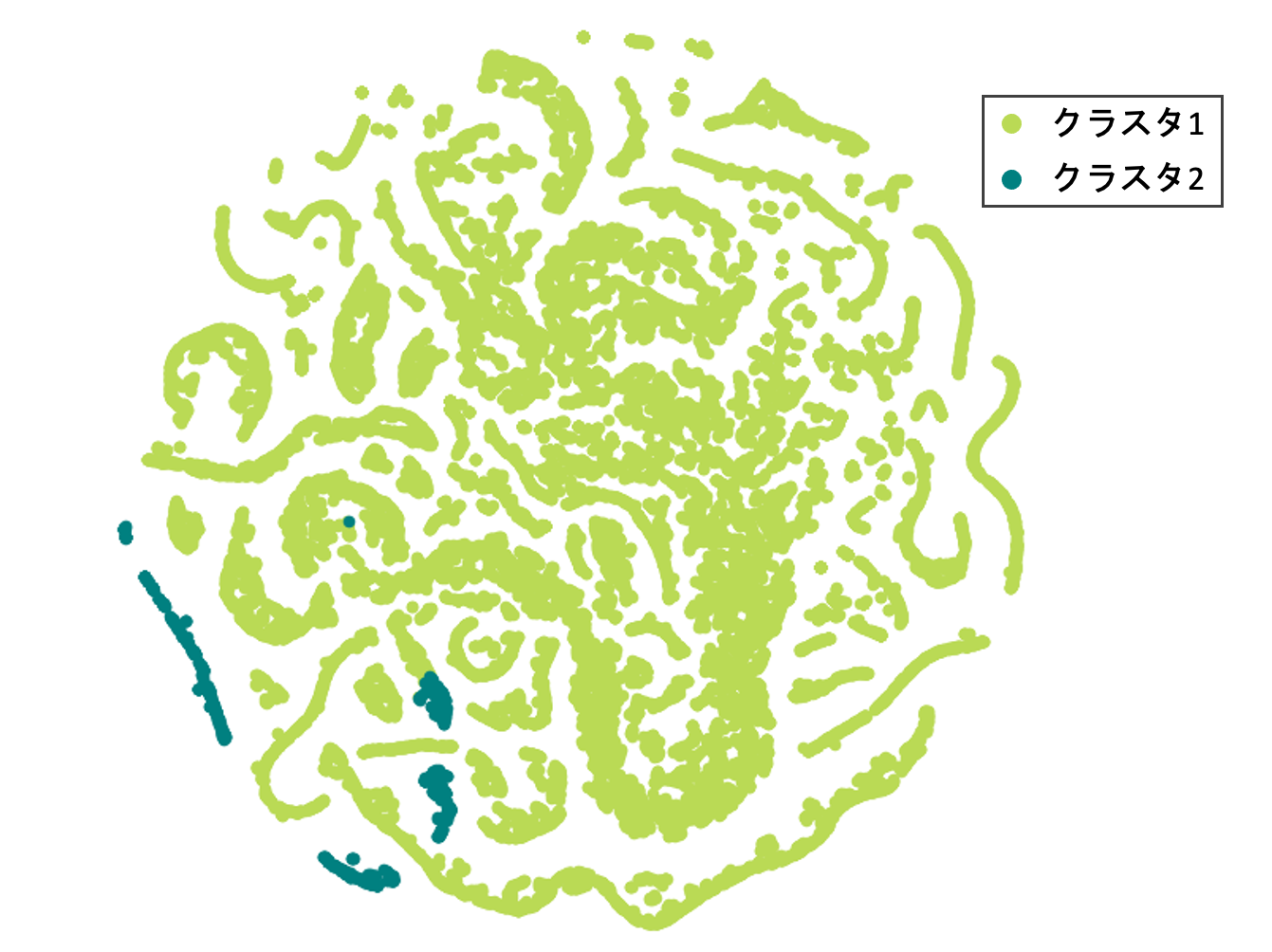
図より、何かしらのクラスタに分類することができていることが確認できます。そこで、各クラスタごとの特徴量の統計量を確認し、意味のあるクラスタに分類できているかを検証します。
各クラスタごとの特徴量の平均値は以下の表のようになります。

(解読しやすくするために、特徴量を絞っています。)
マネーロンダリングのような目的を持ったトランザクションの場合、トランザクションの入力や出力数が大きくなり、入出力シーケンス数も大きくなると考えることができます。また、大きな金額を動かすことが想定されるので、入力や出力の送金額も高額になることが考えられます。これらの仮定を踏まえて、クラスタ2の統計量を確認してみると、説明のような傾向が見られ、不正なトランザクションを見つける足掛かりになりそうなことが分かります。
5. 最後に
今回は、GCNsを用いて不正なトランザクションを分類できるかを検証しました。結果は、GCNsを用いることでビットコインのトランザクションを意味のあるクラスタに分類することができました。ビットコインが健全な使われ方をし、さらに発展してくことを願っています。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。 一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
参考文献
- Kipf, Thomas N., and Max Welling. “Semi-Supervised Classification with Graph Convolutional Networks,” in Proc. of International Conference on Learning Representations (ICLR), pp.1-14, 2017.
- Schlichtkrull, M., Kipf, Thomas. N., Bloem, P., Van Den Berg, R., Titov, I., and Welling, M. “Modeling Relational Data with Graph Convolutional Networks,” in Proc. of European Semantic Web Conference (ESWC), pp. 593-607, 2018.
- S. Pan, R. Hu, G. Long, J. Jiang, L. Yao, and C. Zhang, “Adversarially Regularized Graph Autoencoder for Graph Embedding,” in Proc. of International Joint Conference on Artificial Intelligence (IJCAI), pp. 2609–2615, 2018.
- Kondor, Dániel., Pósfai, Márton., Csabai, István., and Vattay, Gábor., “Bitcoin Transaction Network,” Dryad, Dataset, 2021. https://doi.org/10.5061/dryad.qz612jmcf
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD





