[mathjax]

イントロダクション

次世代システム研究室のT.Yです。
普段は、Hive,Spark,Python+機械学習を駆使して金融ビッグデータを解析して、ビジネスロジックの改善に取り組んでいます。

今回は、本エントリ執筆時点で人工知能分野における世界最大のカンファレンスNipsで発表された最新の深層学習論文の中からピックアップした「Bayesian GAN」をご紹介したいと思います。
この Bayesian GAN は、近年において深層学習の世界に大変なインパクトを与えたGAN(Generative Adversarial Networks)を、ベイズ確率論を取り入れて性能改善を達成した手法です。

[補足1] Nipsについて
Nipsは、Neural Information Processing Systems の略称です。
1986年にカリフォルニア工科大学とベル研究所が設立し、30年もの歴史を持つ国際学会です。
もともとはニューラルネットワークの学会でしたが、現在では機械学習全般をテーマとして扱っています。
参加人数は2016年に5,000人、2017年には8,000人と、指数関数的な勢いで増えており、人工知能分野では世界最大の学会となっています。
https://nips.cc/

[補足2] GANについて
GANは、Generator(生成器)とDiscriminator(鑑識器)が互いに競い合いながら学習を進めるというメカニズムを持ち、写真やイラスト、音声を自動合成することができます。そのインパクトは大変強く、多くの研究者がさまざまな改良に取り組んでいます。

GANがどのようなものかを具体的に知りたい際には、私が以前発表した以下のスライドをご覧ください。

Bayesian GAN が解決する「最頻値崩壊(mode collapse)」

GANは、本物そっくりの画像を生成するインパクトを引っさげて、あっという間に深層学習の世界で普及しました。
研究者の興味関心を強くひきつけるGANですが、難しい問題を複数抱えています。
その中の一つに最頻値崩壊(“mode collapse”)という、特定パターンに極度に偏ったデータ生成しかできなくなる問題があります。

modeとは最頻値のことであり、文字通り最も頻繁に出現するパターンしか生成できない学習に陥ってしまいます。
具体的に言うと、どのようなインプットを与えても、出てくる画像や音声はほぼワンパターンに収束してしまうのです。
GANではDiscriminatorの学習がGeneratorよりも早く進む場合があり、GeneratorはDiscriminatorを欺くことが出来るわずかなパターンを選択的に生成するようになります。
よって、本物そっくりの画像や音声を合成できるものの、ワンパターンしか出力できないモデルが出来上がります。

こうした背景があるため、従来のGANにおいては、成功するモデルが出来るかどうか運試しの要素が多分にあり、何度もモデル構築を試す羽目になることは珍しいことではありませんでした。

これまでの改善の取り組み

GANが抱える問題に対して、いくつかの改善アプローチが提案されてきました。

1. Wasserstein GAN
【論文はこちら】

Wasserstein距離という数学的概念を導入し、学習の偏りを解消しようというアプローチです。
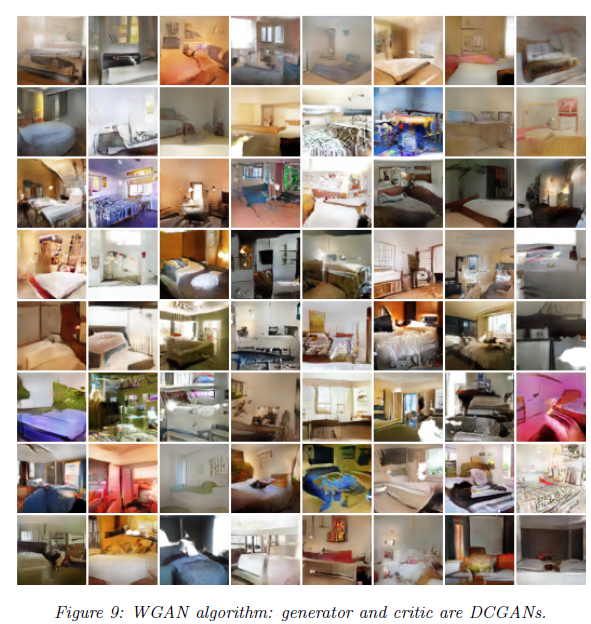
学習したデータの特徴を満遍なく取り入れようとしており、生成されるデータの多様性は、従来のGANやDC-GANより優れているようです。

Wasserstein GAN による生成画像サンプル(論文より引用)

---

従来の GAN による生成画像サンプル(論文より引用)

2. unrolled GAN
【論文はこちら】

従来のGANにおいて、DiscriminatorがGeneratorより早くレベルアップしがちな現象に着目し、Generatorを前もってある程度学習させておくというアプローチです。
Generatorにどれくらいのアドバンテージを事前に与えるかによって、生成される画像の多様性とクオリティが変化します。
以下のサンプル(上記論文より引用)では、従来のGAN（画像下段）が学習の結果、ワンパターンしか出力できていないのに対して（＝これが mode collapse)、 unrolled GAN(画像上段)では様々なパターンが生成されていることが分かります。

Bayesian GAN はどのようにして mode collapse を解決するのか

基本的な戦略

Bayesian GANは、どのようにして多様性を保ったままGeneratorを学習させることができるのでしょうか？
鍵を握るのはベイズ確率論の事後確率と、モンテカルロ法です。
具体的には、確率的勾配ハミルトニアンモンテカルロ法(Stochastic Gradient Hamiltonian Monte Carlo:以降、SGHMCと略)を使い、Generatorが多様な出力ができるように学習を進めていきます。
ベイズ確率論を用いたアプローチをもって、Generatorがmode collapseに陥らないように逐次的にパラメータ（＝ニューラルネットワークの重み行列）を更新します。
Discriminatorを欺けるほど精巧で、なおかつ多様性をもった出力ができるパラメータをベイズ確率論を使って上手に探そうというわけです。

そして最も特徴的であると私が考えているのが、Generator と Discriminatorの学習競争の構造です。
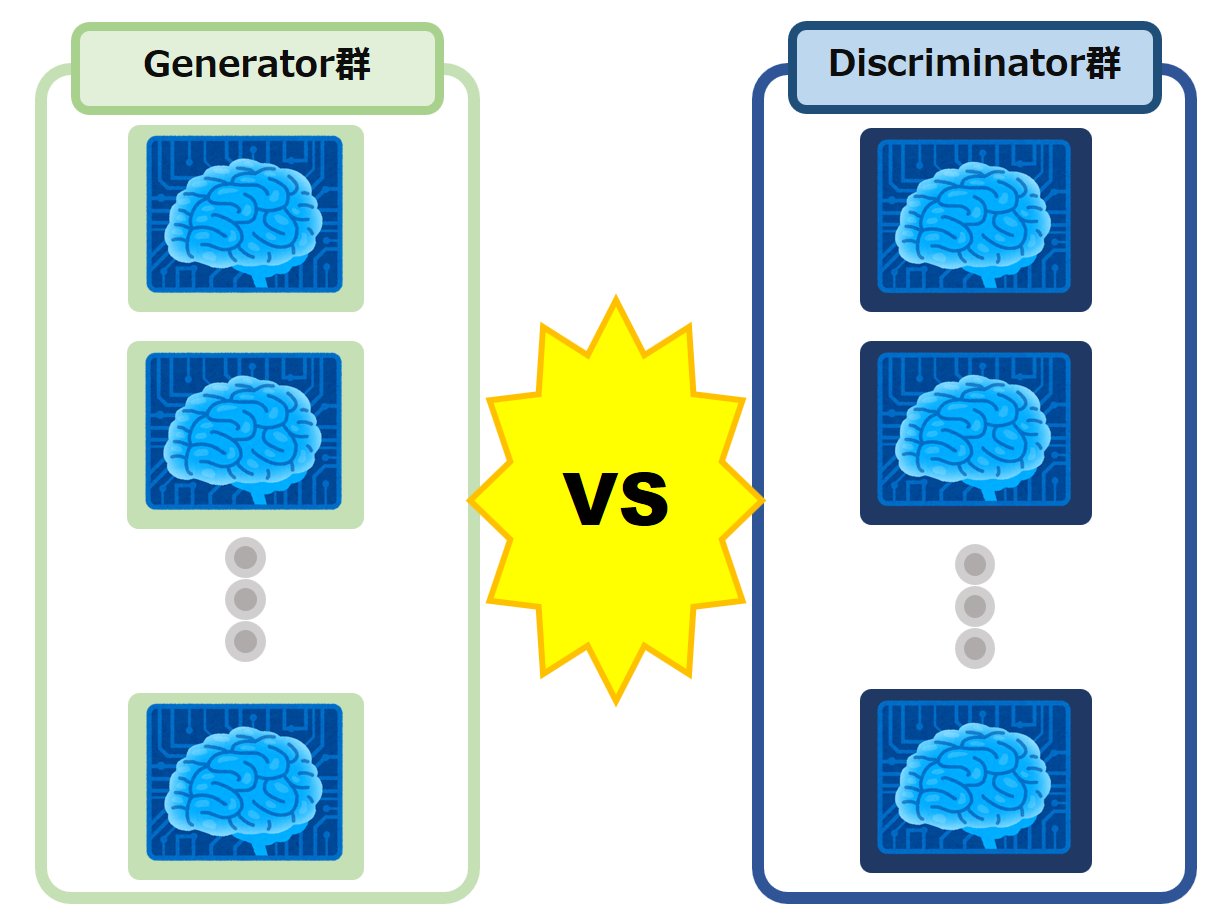
従来のGANが、1対1で対決して競い合っていたのに対して、Bayesian GAN ではなんと多数　対　多数、すなわちチーム戦で競い合って学習しています。
この「多数　対　多数」と構造が、生成される出力の多様性とクオリティを両立する上でかなり重要なポイントになっていると考えられます。

Bayesian GAN における学習競争の構造:

従来のGANとBayesian GANの多様性の差

従来のGANでは、一組のGeneratorとDiscriminatorが競い合って学習します。
学習が進むと、やがてGeneratorは Discriminatorが苦手とする特定のパターンを集中的に生成する方向に学習していきます。
そして、再現できるのは入力した元データ（画像や音声）のうち、ごく一部のパターンだけという mode collapseの問題に陥りやすくなります。
一組のパラメータを更新してゆく関係上、局所的な最適解につかまってしまうことが少なくありません。

一方、Bayesian GAN では、多数のGeneratorと多数のDiscriminatorが総当り戦的に競争して学習していきます。
そのため、学習が進んでも、多数のGeneratorがいるので生成されるデータに多様性があります。
また、個々の学習過程においても、一つのDiscriminator相手にフォーカスした学習ではなく、多数のDiscriminator相手に満遍なく勝てるようにバランスを保った学習をするようになります。

各Generatorをθgというパラメータで定義し、各θgに対応するGeneratorがDiscriminatorを欺くことができる（＝十分に本物に近いデータを生成できる）確率をP(θg|D)とします。
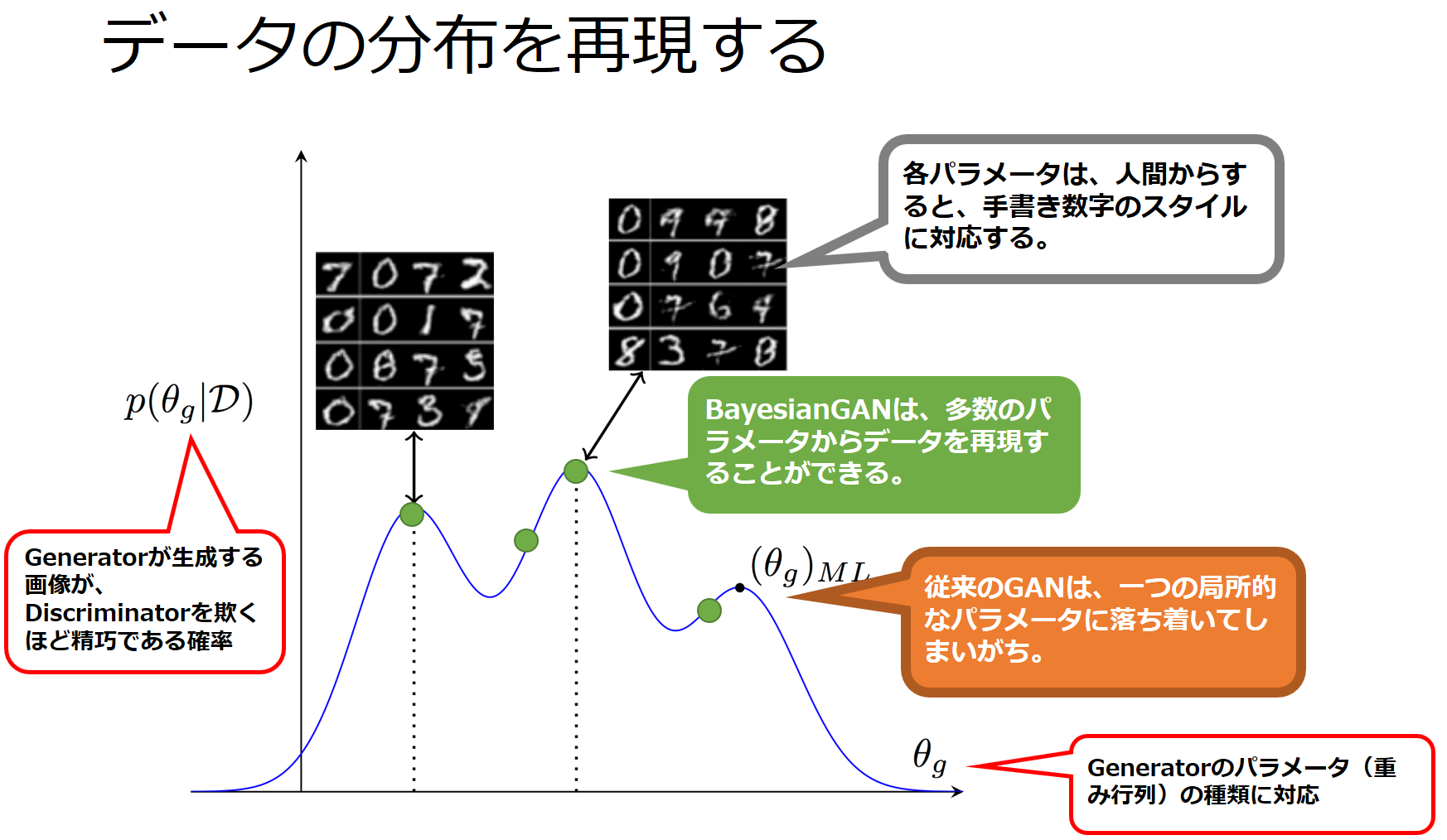
従来のGANとBayesian GANのGeneratorの性能の違いは、手書き数字の再現を例にして、次の図のように表すことができます。

※元図は、Bayesian GAN 論文より引用

従来のGANは、(θg)MLという一点だけのGeneratorを構築するのに対して、Bayesian GANは、様々なθgに対応するGeneratorを構築できるのです。

ベイズ確率論をどのように活用するか

手法名に”Bayesian GAN”と銘打っているわけですが、どのあたりがベイズなのでしょうか？
Generator、Discriminatorの学習に、事後確率、事前確率の概念を導入していることが最も端的なベイズ的特徴と言えるでしょう。
Bayesian GANにおいて多数のGenerator、Discriminator同士の競争をモデル化するに当たり、ベイズの定理は効果的な役割を果たしています。

論文中からBayesian GAN で使われているベイズ定理に沿った式を紹介します。


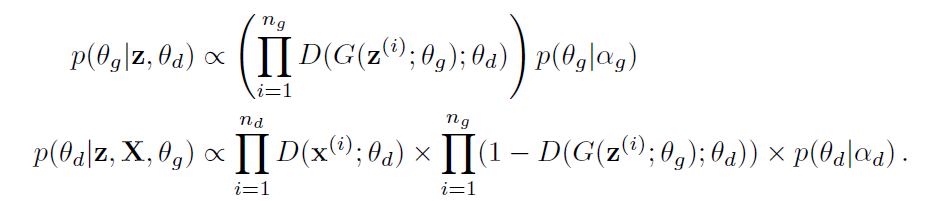
上の式は、Generatorが生成した画像がどれくらいDiscriminatorを欺いたのかを表す事後確率の式です。
下の式は、Discriminatorが本物を本物と認識し、Generatorが生成した画像をニセモノと見抜く確率を表した事後確率です。
数式中の各要素の説明は以下の通りです。

---

$$
X：学習データを構成する本物の画像。X={x^1,x^2,…,x^N} \\
x^i はXに含まれる個々の画像である。\\
\\
n_{g} : Generator側のバッチサイズ\\
n_{d} : Discriminator側のバッチサイズ\\
z: ノイズベクトル列。z^(1),z^(2), … z^(i) は個々のノイズベクトルである\\
G(z;θ_{g}):ノイズzが与えられた時、パラメータθ_{g}にしたがって再現された画像\\
D(x; θ_{d}):入力画像xが、学習データに含まれる本物の画像である確率を、パラメータθ_{d}にしたがって計算したもの\\
D(G(z(i);θ_{g}); θ_{d}):ノイズz(i)とパラメータθ_{g}から再現された画像が、本物の画像とみなされる確率(=誤った判定がされる確率)\\
$$

---

このように定義された事後確率は、それぞれGeneratorおよびDiscriminatorの性能を定量化するのに用いられます。
この事後確率を評価関数として、深層ニューラルネットワークを最適化することになります。

Bayesian GANではｍ上記事後確率をSGHMCと組み合わせて、次のような学習アルゴリズムを実行します。

ループ処理を通して、Generator群とDiscriminator群を総当り戦で比較・競争して、重みパラメータを更新していることが分かります。

実験結果

それではBayesian GANがどれくらい性能改善を達成できたのか実験結果を見ていきましょう。

実験用コードは、論文著者がGitHub上で公開しています。
理解を深めたい方はぜひ実行してみましょう。
https://github.com/andrewgordonwilson/bayesgan

出力する画像の多様性の比較

多様性を視覚的に把握しやすくするため、各画像をPCA（主成分分析）という手法を用いて2次元平面上にプロットします。
具体的には、各画像を2次元の成分(x,y)に集約して平面上にプロットします。

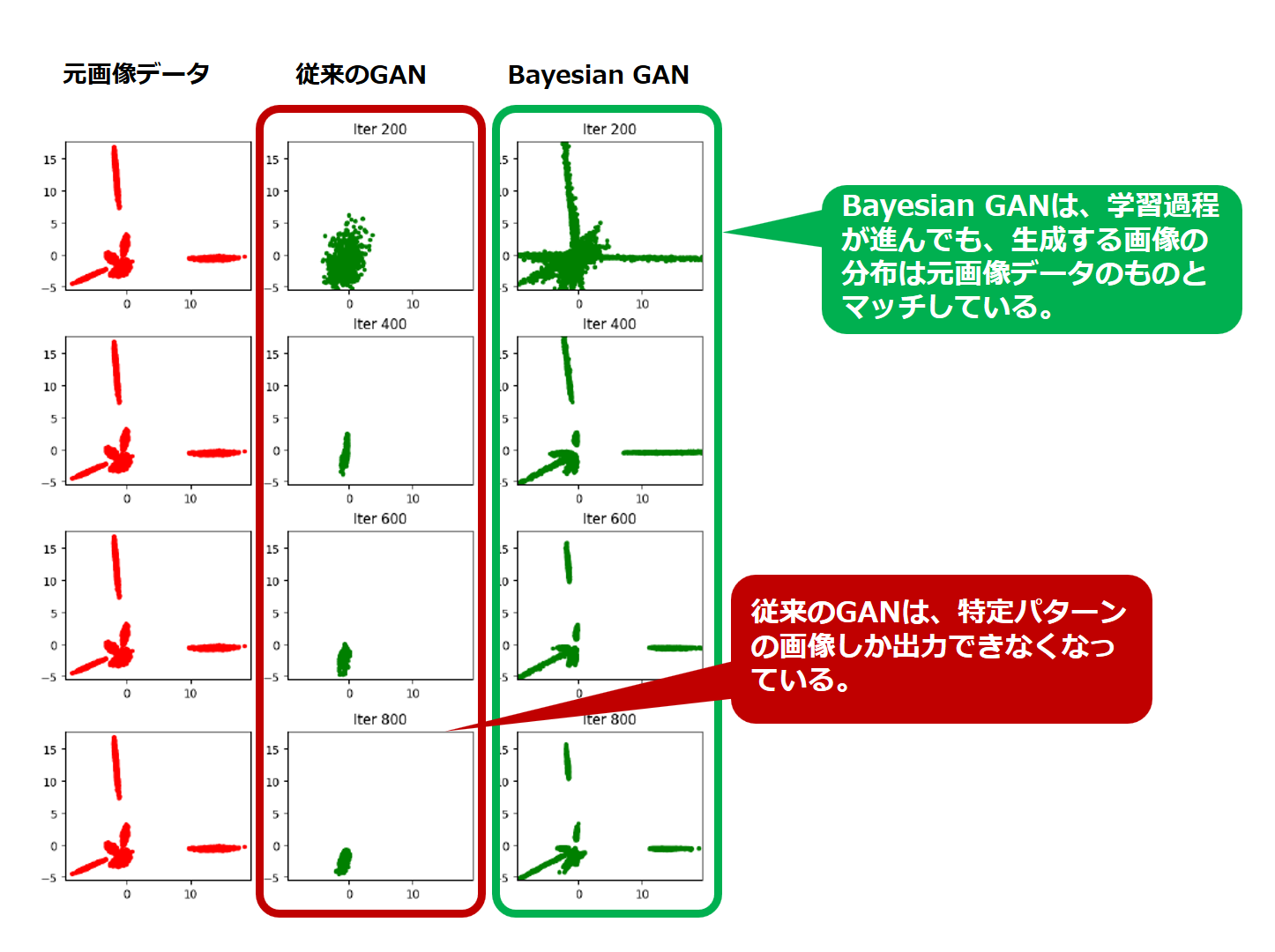
以下の図をご覧ください。
左端は、実験に用いた画像データ集の多様性をプロットしたものです。
真ん中の列は、従来のGANが出力した画像の多様性をプロットしたものです。
右の列は、Bayesian GANが出力した画像の多様性をプロットしたものです。

図を見ると、従来のGANの多様性が特定の領域に偏っています。
従来のGANは、多様性が偏る、すなわち mode collapse が発生していることが伺えます。
一方、Bayesian GANは、元画像データの多様性とほぼオーバーラップする分布になっていることが分かります。
学習した画像データ集をよく再現できていることが伺えます。

生成画像の精度の比較

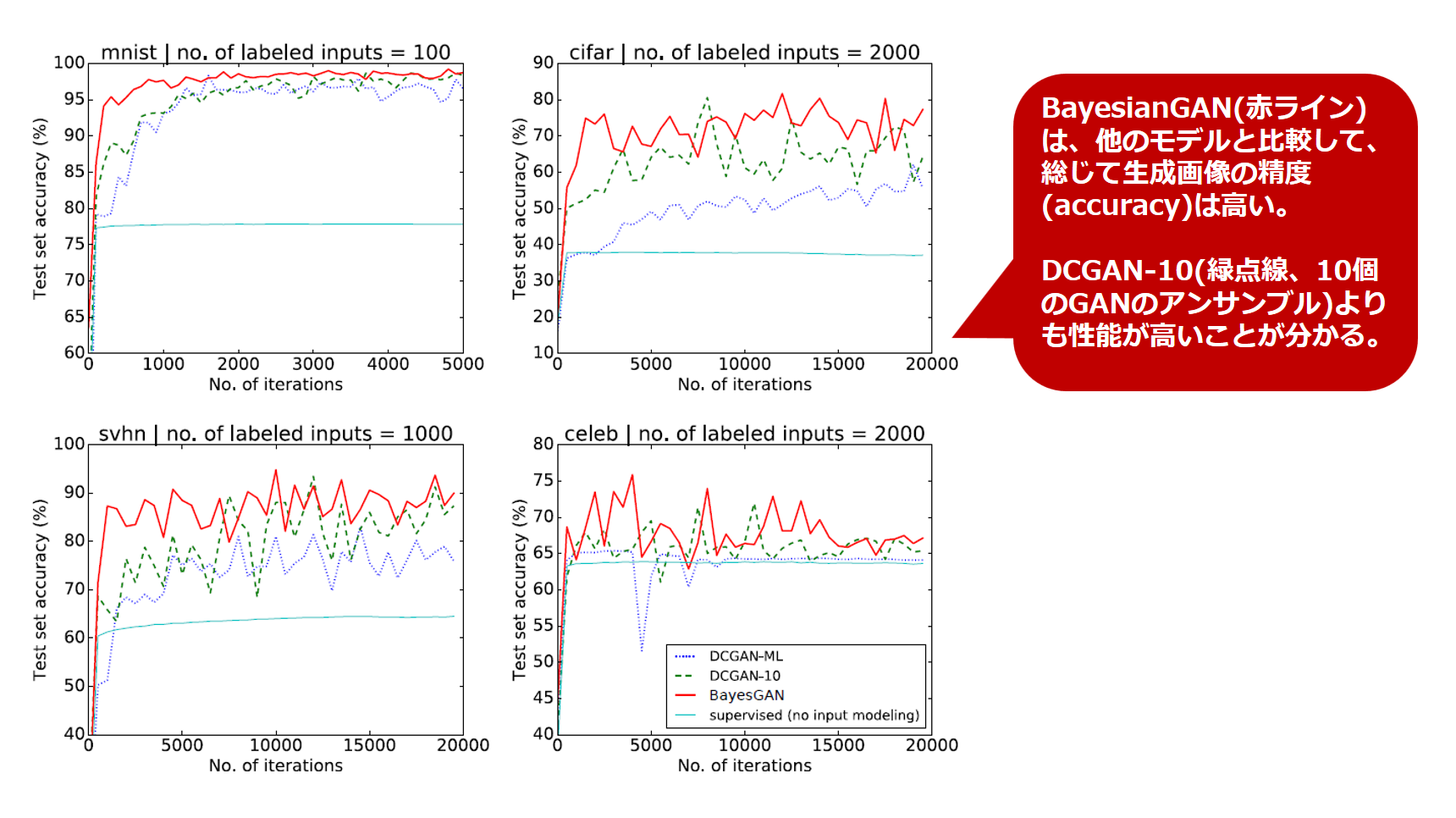
続いてGeneratorが生成する画像の精度を比較します。
実験対象となる画像データは、機械学習分野でお馴染みの MNIST,CIFAR10,SVHN,CelebAの各データセットです。
実験結果をまとめた図は以下の通りです。
学習過程の進行に合わせて上下しながら、Bayesian GANの精度が押しなべて既存手法の精度を上回っていることが分かります。

まとめ

Bayesian GAN は、ベイズ確率論を取り入れたアプローチで、「生成するデータの多様性」と「生成データの精度（＝再現度の高さ）」を両立していることが示されました。
その両立は、複数の Generator、Discriminatorを総当り戦で競い合わせることで実現できていることが分かりました。
ナイーブベイズフィルタをはじめとするベイジアンフィルタという伝統的な機械学習モデルのコンセプトが深層学習と結びつき、より良い性能を実現する道が開かれたことには感慨を禁じえません。
GANの生態系は今後、更なる発展を遂げることでしょう。
今後が大変楽しみな分野です。

【重要】最後に

次世代システム研究室では、機械学習や統計処理に関心を持つ開発者、アーキテクト、データサイエンティストを求めています。
自由闊達にのびのびと働きながら学べる環境があります。
コーヒー片手にアカデミックとビジネスの融合したディスカッションをしながら、知的好奇心を満たすことができる環境があなたを待っています。
次世代システム研究室にご興味を持たれたらすぐに 募集職種一覧 からご応募してください。
皆さんのご応募をお待ちしています。