こんにちは。次世代システム研究室のK.S.（女性、外国人）です。

今回は新型コロナウイルス感染者のデータを利用しながら生存分析（Survival Analysis）を勉強します。
（前提：このブログは技術勉強の目的であり、分析結果に深刻になりすぎず、技術参考程度に結果を大目に見て下さい）

withコロナの日常生活には慣れてきたでしょうか。

正直、私は全く慣れずに、どう生活すべきか未だ少し不安が続いています。飽きるくらいニュースで感染者が増えたり減ったりこの先はどうなっていくのか予想がつきません。個人的には最近の感染者数には関心がなく、むしろ、もし自分が感染してしまったら、死ぬ確率、退院までの時間がどれくらいなのかが気になってきました。人生の生き残り時間を予測できれば、効率よく時間の優先的な使い方ができるかもしれないと思いました。

というわけで、今回は病気などに感染したら、生物の生存や回復時間の分析手法といった生存分析を勉強することにしました。そこで、新型コロナウィルス感染者のデータを分析してみました。

さて、このブログの構成は以下の通りです。

①生存分析（Survival Analysis)とは
②新型コロナウイルス感染者データで生存分析をしてみた
③まとめと考察

①生存分析（Survival Analysis)とは

生存分析（Survival Analysis）は生物の死亡や機械の故障などのイベント（起きる、起きない）ということに対して、要因をもつことにより発生するまでの期間を分析するための統計的な手法の一つです。ときとして、time-to-event分析をと呼ばれています。生存分析は様々な分野で幅広く利用されています。具体的な例ですと、医療関連によるがんの感染者の生存時間分析、エンジニアリングによるパソコンの部品ごとの故障時間予測、マーケティングによる顧客の解約タイミング予測、保険による顧客の死亡期間の確率の評価、などです。

では、どのように生存時間を分析するのかを説明したいと思います。

生存分析を行うためには、主な３つの要因を考える必要があります。①Event and Survival time（イベントと生存時間）、②Censoring（打ち切り）、③ Survival and Hazard functionです。

 

Event and Survival time（イベントと生存時間）

イベントとは病気による死亡や機械故障などのことです。生存時間はスタートをしてから終了までの期間です。生存分析はスタート（病気発症や機械利用開始）から、イベントの発生（死亡や故障）までの時間のデータを分析します。細かく言うと、今回のような病気関連分析の場合、イベントは死亡だけではなく、「回復、再発、進行」までという要因も考えられます。

 

Censoring（打ち切り）

Censoringは治療の予後に関する調査などで、生存のまま研究終了を迎えることです。上記のような、生存分析では病気の発症から再発や死亡までを中心に分析しますが、研究期間内では、全てのイベントが終了までを観察される訳ではないので、研究期間を終了しても、考慮外の理由で結果（再発するか、死亡するか）は特定できないままの状況はcensoringということになります。ちなみに、censoringは生存分析の強みで、完璧なデータ取得が難しい場合は他の統計手法より適用しやすい柔軟なコンセプトです。

 

Survival and Hazard function

Survival and Hazard functionは生存を確率的に表すための数式です。

Survival functionはイベントの発生まで、ある将来の時間までの生き残りを確率的な関数で表すものです。具体的な例で人の寿命を考えます（下記の図を参考）。イベントは死亡です。数式で説明すると、Tは調査中の人口からの取得したランダム寿命です。S(t)はsurvival functionで、tの時に死亡イベントの確率（Pr）がまだ起こらないと定義されます。イメージ的にSurvival functionからの結果をプロットすると、X軸は生まれてからの年数、Y軸は死亡イベントがまだ起こっていない確率です。このSurvival functionによる、40歳のときに、人口の75%くらいはまだ生きるいうことが分かります。

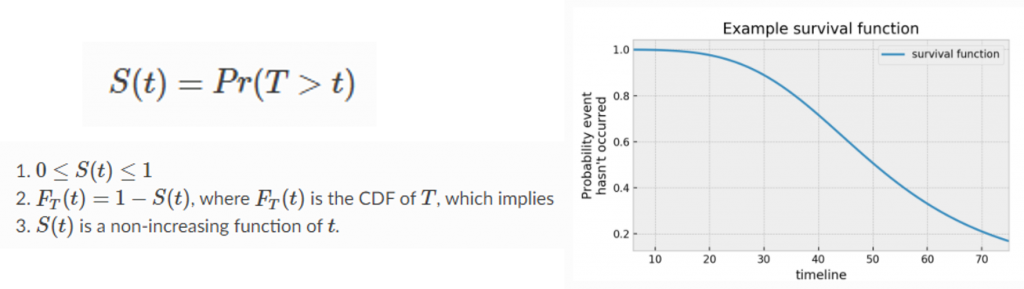
参考：https://lifelines.readthedocs.io/en/latest/Survival%20Analysis%20intro.html

 

Hazard functionはある時のイベントの確率です。例えば、人間は生まれてからおおむね60年後に亡くなります。もし、1000人の中に40年、生きる人たちが30人いると、hazardは0.03になります。60年で生きる人たちが45人いると、hazardは0.045になります。ちなみに、40年生きる人たちは60年生きる人たちの組には入っていません。また、計算するときに、60.01年か60.02年かは実質的に同じと考えられ、Hazardは1,2,3…, 100年のような形で計算します。式を書くと下記のような感じになります。また、Cumulative Hazard「H(t)」はHazard「h(t)」の累計になります。Cumulative Hazardを使ってSurvival functionを計算することもできます。

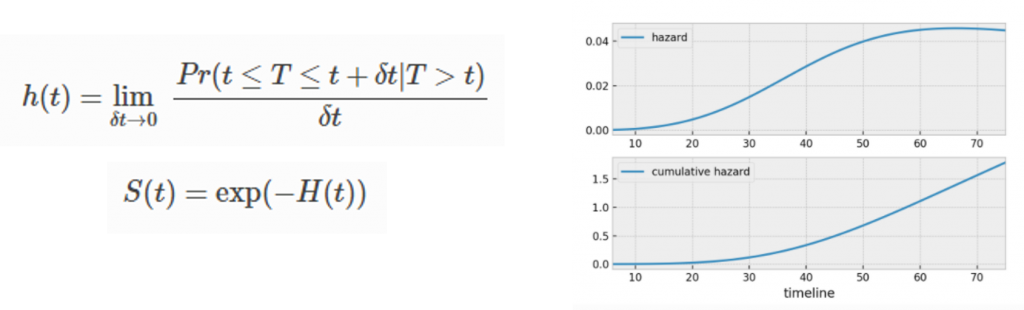
参考：https://lifelines.readthedocs.io/en/latest/Survival%20Analysis%20intro.html

 

繰り返しますが、Survival functionはイベントがまだ起こっていないことに注目しますが、hazard functionは起こっているイベントに注目します。この２式の関係は下記のイメージになります。

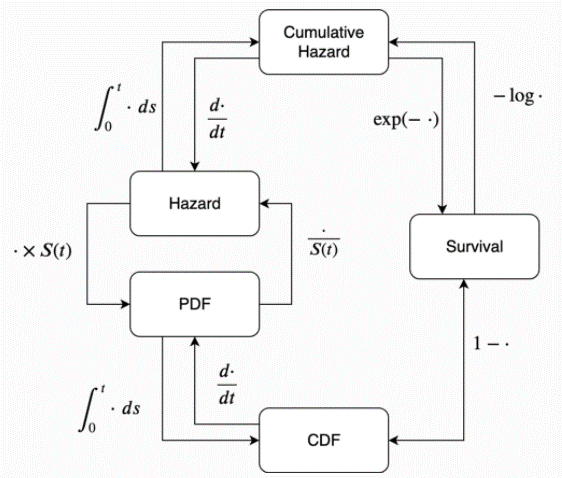
参考：https://lifelines.readthedocs.io/en/latest/Survival%20Analysis%20intro.html

 

上記の人生の寿命の例は単純化されたものですが、実際の病気例等はある時刻に対してどれくらいの生存確率があるのかに興味があります。そのため、観察データを利用してSurvival and Hazard functionを推定します。推定するための手法は沢山ありますが、よく使われているのはKaplan-Meier法とCox proportional hazards法です。この記事を参考にし、有名な二つの手法を紹介します。

 

Kaplan-Meier法

Kaplan-Meier法はSurvival functionを推定するため、医療調査や基礎研究でよく使われている簡単な生存分析手法の一つです。例として、ユーザがwebsitesを開いてから閉じるまでの時間の解析を挙げます。観察時間は6分、ユーザが６人いて、その中の２人は観察時間を超えても結果が出ない（打ち切りの）人とします。下記の図を参考にしながら、説明します。Kaplan-Meier推定量はSurvival functionを利用します。X軸はイベントの時刻、Y軸は推定された生存確率です。まず、t=0から2.5までt=0でイベントが起こる数(di)すなわちwebsiteを閉じたユーザは0人、リスクがあるユーザ数（ni）すなわちwebsiteを閉じないユーザは6人ですので、S(t)=1になります。次に、t=2.5から4.0までt=2.5でイベントが起こる数(di)は1人、t=2.5までにリスクがあるユーザ数（ni）は6人ですので、S(t)=0.83になります。このような流れで計算していって、どの時刻で生存確率がどれくらい残っているのかを推定します。


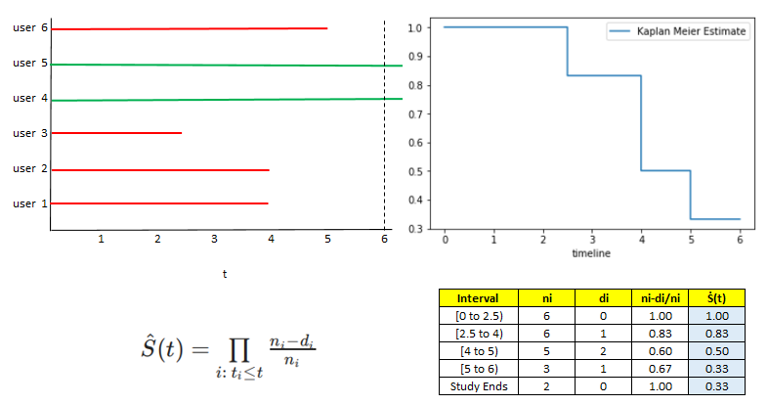
参考：https://towardsdatascience.com/survival-analysis-intuition-implementation-in-python-504fde4fcf8e

上記のような、計算を繰り返すと、Survival functionを計算することが可能になります。

 

Cox’s proportional hazards法

Cox’s proportional hazards法はKaplan-Meier法より複雑になってきます。Kaplan-Meier法はイベントの生存時間を分析しますが、一般社会ではイベントの生存時間だけではなく、イベントが起こるのに様々な要因（特徴量）があります。例えば、上記のユーザがwebsitesを見る例には実はユーザの年齢や性別や国籍なども関係があります。Cox’s proportional hazards法はそれらの要因を考えて推定します。数式は下記のようになります。


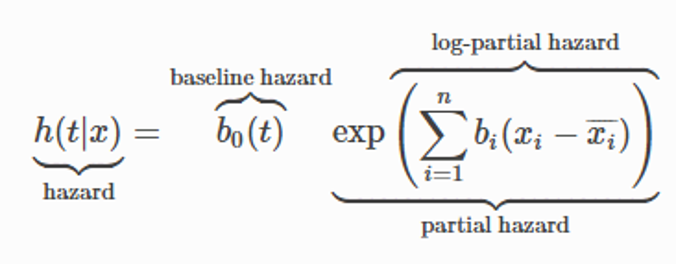
この手法の独創性はlog-partial hazardを投入することです。log-partial hazardは各サンプルで様々な要因を線形で計算します。それから、要因の関数を時間とともに変更するhazard function（baseline hazard）を組み合わせて計算します。こうすることで、様々な要因を考慮しながら、生存時間を分析することが可能になります。

 

②新型コロナウイルス感染者データで生存分析をしてみた

それでは、いよいよ、実装です。

やりたいことは新型コロナウイルス感染者のデータを利用し、生存分析をしてみることです。
全ての実装コードはgithubに置いてありますので、詳細はそちらを参考にしてください。

 

実装環境

今回の実装では、Google Colaboratoryを利用しました。また、生存分析はlifelinesを利用しました。

 

データ

韓国政府が公開した新型コロナウィルス感染者情報を利用しました。

データは5165人の患者さんのもので、患者さん一人ずつにIDを付け、各IDには性別、年齢、国籍などが入っています。また、病気が特定できた日や退院日もあり、回復や死亡などの情報もあります。


 

データ処理

生存分析で分析したい条件に合わせて下記のデータ処理を行いました。
・新型コロナウィルスの感染を特定できた日から、退院や死亡（イベント）までの期間を計算します。
・イベントのフラグを付けます。イベントが起こらない患者さんはcensoringとして扱います。
・情報が入っていないデータは削除します。

df = df[["sex","age","confirmed_date","released_date","deceased_date","state"]]
df["released_date"] = df["released_date"].astype("datetime64[ns]")
df["confirmed_date"] = df["confirmed_date"].astype("datetime64[ns]")
df["deceased_date"] = df["deceased_date"].astype("datetime64[ns]")

# calculate time 
df.loc[df["released_date"].notnull(), "timeline"] = df["released_date"] - df["confirmed_date"]
df.loc[(df["state"]=="deceased") & (df["deceased_date"].notnull()), "timeline"] = df["deceased_date"] - df["confirmed_date"]
df["timeline"] = pd.to_numeric(df['timeline'].dt.days, downcast='integer')
print ("time min:{}, max:{}".format(df["timeline"].min(), df["timeline"].max()))    

# duration has to be non-negative number
df = df.drop(df[df["timeline"]<0].index)

# censoring
df["event"] = np.where(df["state"]=="isolated", 0, 1)

# deceased
df["death"] = np.where(df["state"]=="deceased", 1, 0)

# manage null data
df = df.dropna(subset=["timeline"])
df.reset_index(inplace=True)

 

データ可視化

処理したデータを可視化してみました。下記の結果によると、死亡患者さんも回復患者さんもいて、死亡か回復か特定できない患者さんもいました。


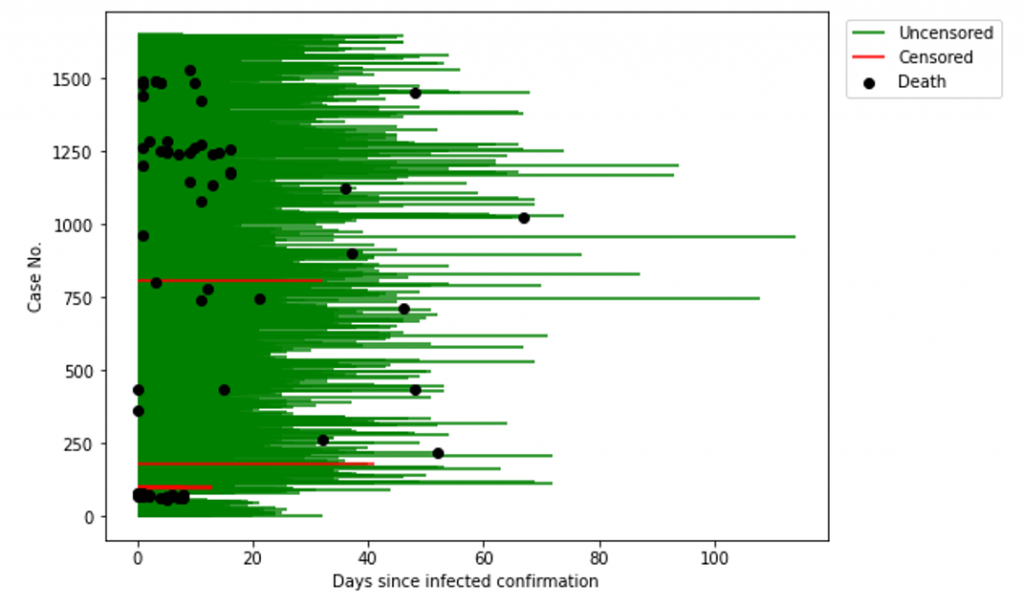
分布でプロットしてみると、だいたい20日前後で退院できた患者さんが多いということが見られました。

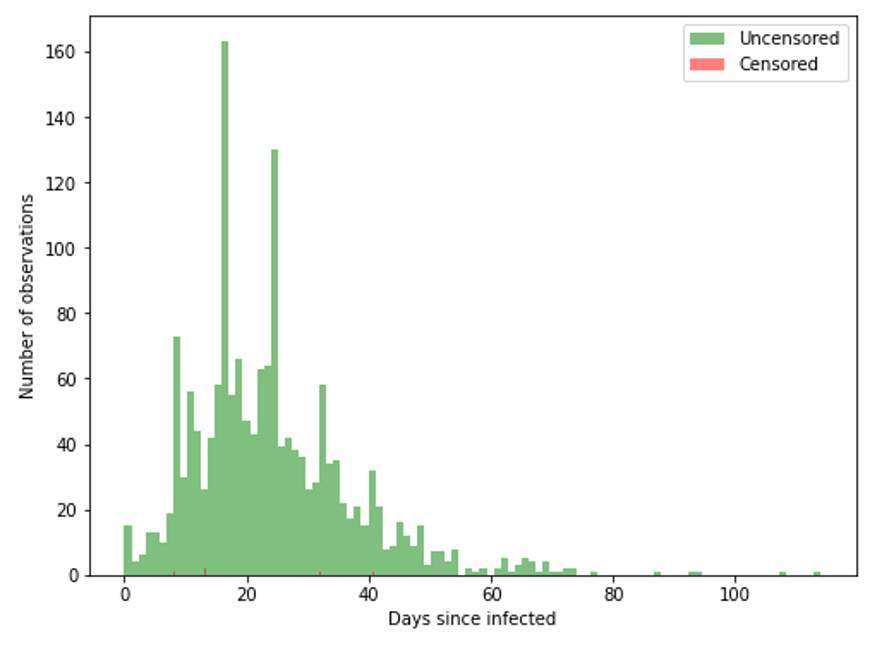
実装

処理したデータを利用し、上記で紹介したKaplan-Meier EstimateとCox Proportional Hazard Modelを試してみました。

Kaplan-Meier Estimate

まず、全部のデータでSurvival functionを計算してみました。

from lifelines import KaplanMeierFitter

df_km = df.copy()

# Create a kmf object
kmf = KaplanMeierFitter() 

# Fit the data into the model
durations = df_km["timeline"].values
event_observed = df_km["event"].values
kmf.fit(durations, event_observed,label='Kaplan Meier Estimate')

# Create an estimate
kmf.plot(ci_show=True) # ci = confidence interval

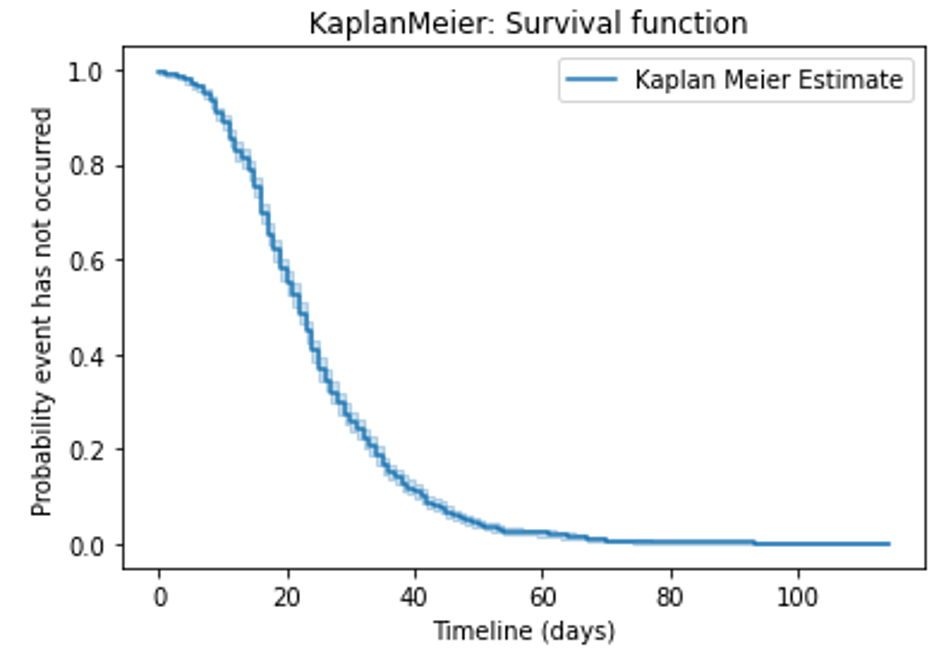
次に、回復と死亡の条件を分けて分析してみました。

ax = plt.subplot(111)
kmf.fit(df_km[df_km["death"]==0]["timeline"].values, df_km[df_km["death"]==0]["event"].values,label='Recovered')
kmf.plot(ax=ax) 

kmf.fit(df_km[df_km["death"]==1]["timeline"].values, df_km[df_km["death"]==1]["event"].values,label='Death')
kmf.plot(ax=ax)

plt.xlabel("Timeline (days)")
plt.ylabel("Probability event (Recovered or Death) has not occurred")
plt.title("Survival function");

結果、死亡のときの方が生存期間が短かったことが見られました。つまり、死亡の場合は20日以内でほぼ生き残れない結果でした。全体的な確率ですが、もし、自分が感染してしまって、20日以上入院してまだ死ななかったら、たぶん生き残れるのではないかと勝手に思ったりしました。

 

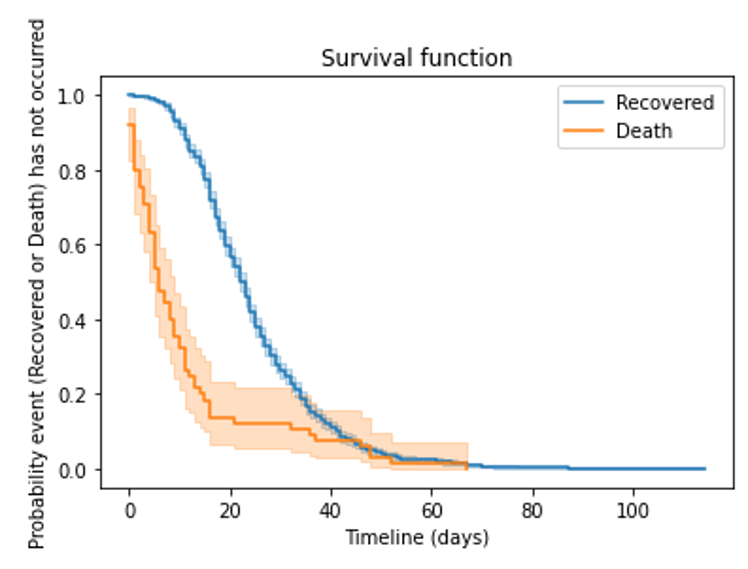
Cox Proportional Hazard Model

ここでは、Cox Proportional Hazard Modelで年齢と性別の要因を入れてもう少し細かい分析を試したいと思います。

# process data
df_cox = df.copy()
print (df_cox.columns)
df_cox = df_cox.drop(columns=["index","confirmed_date","released_date","deceased_date","death","state"], axis=1)
df_cox = df_cox.dropna()
 
# encode string data
le = LabelEncoder()
le.fit_transform(df_cox[['sex']].values)
sex_dict = dict(zip(le.classes_, le.transform(le.classes_)))
print(sex_dict)
le.fit_transform(df_cox[['age']].values)
age_dict = dict(zip(le.classes_, le.transform(le.classes_)))
print(age_dict)
 
df_encode = df_cox[['sex', 'age']].apply(le.fit_transform)
df_cox = pd.concat([df_cox[["timeline","event"]], df_encode], axis=1)
df_cox.head()
 
# fit cox model
cph = CoxPHFitter()
cph.fit(df_cox, duration_col='timeline', event_col='event')
cph.print_summary() 

結果は下記になります。結構個人差が見られました。


 

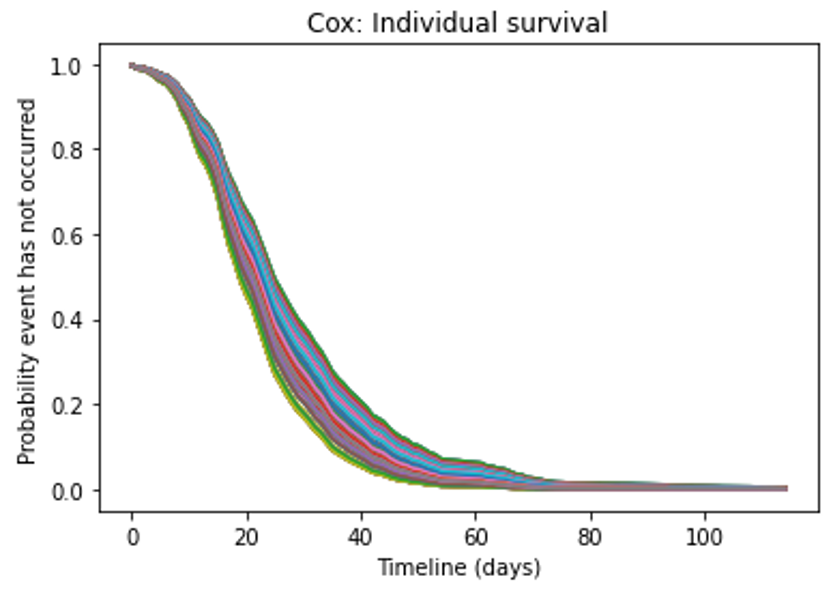
次は年齢や性別を分けてみましょう。結果、年齢の場合は違いが見られますが、性別の場合はあまり見られませんでした。


 

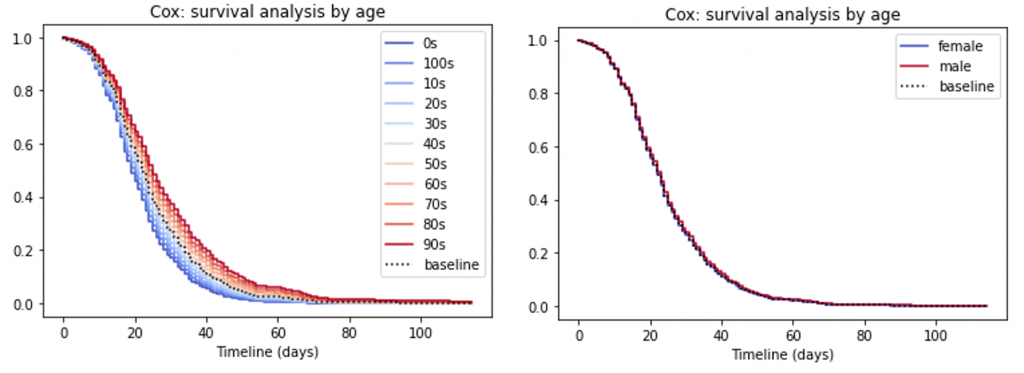
最後に、自分とたまに遊んでもらっている小さい友達の条件に合わせて比較してみたいと思います。

モデルに自分の「30代、女性」条件と小さい友達「2歳、男性」を入れて、予測してみました。結果は下記になりました。確率的に、自分の退院までの時間はちびっ子より長いようです。やはり、子供の元気さにはかないません。

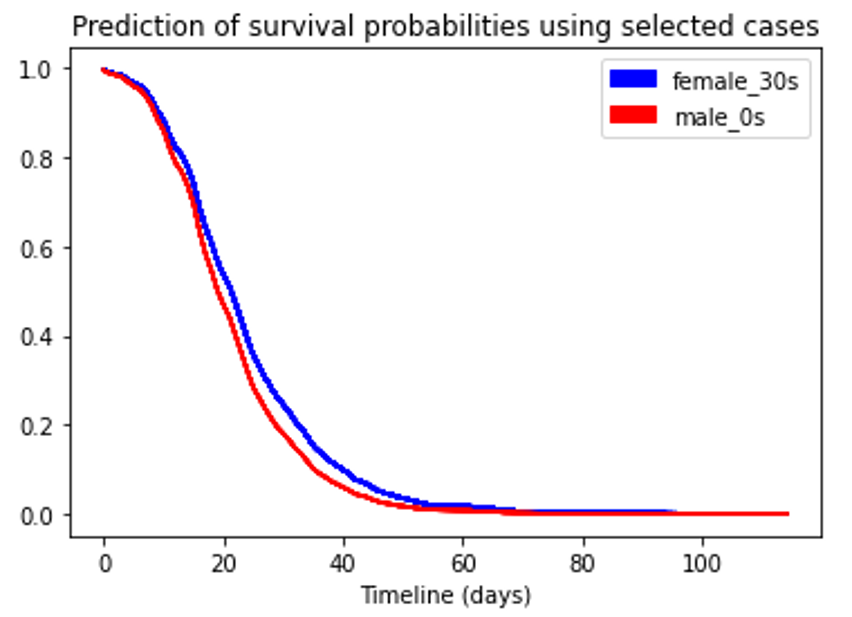
③まとめと考察

今回は生存分析を紹介しました。生存分析は技術的には新しいものではないですが、今のコロナ状況で役に立つ分析かと思います。

最後に

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。