量子自然言語処理〜量子回路で文章を理解する〜

こんにんちは、次世代システム研究室のT.I.です。

前回のBlogでは、現在実用化されている量子コンピュータ(NISQデバイス)の機械学習への応用を紹介しました。今回も引き続き量子コンピュータの話題として、量子計算に基づいた自然言語処理(参考文献 [1-5]) について解説したいと思います。

TL;DR

最近、量子コンピュータを用いた自然言語処理の実証実験がCambridge Quantum Computing (CQC) によってなされました。
この量子自然言語処理のモデル(DisCoCat)では、文章を単語のネットワークに書き換えて、それを量子回路に変換し実行します。その出力結果を文章の真偽として、教師データを元に量子回路のパラメータを学習させます。その結果、簡単な推論タスク(ex. Alice is rich. & Alice loves Bob. ⇒ Is Alice who loves Bob rich ?) に対して正解を回答できました。
ただし、現在の量子コンピュータ・デバイスでは、数個の語彙の簡単な文章までしか処理できないため、直ちに実用的なタスクに応用することは中々に難しそうです。本格的な実用化には今後の量子コンピュータの発展が不可欠です。

自然言語処理とは

近年、機械学習で最も注目されている分野の１つです。以前のBlogで紹介したように、Attention というニューラル・ネットワークの構造を応用したBERT、そして最近ではGPT-3といった大量の学習データに基づく高性能なモデルが続々と誕生しています。

Distributional Model

機械学習で文章を処理するためには単語の意味を学習させる必要があります。Word2Vecのようなアプローチでは、大量の文章を元に共起される単語を統計的に分散表現(distributional representation)を抽出します。その結果、単語は高次元空間のベクトル(Word Vector)として表現されます。単語間の類似度などの関係性を定量的に比較したり、以下のような単語間の意味の足し算・引き算の計算ができます。

$\begin{align*} \overrightarrow{\mathrm{king}} - \overrightarrow{\mathrm{man}} + \overrightarrow{\mathrm{woman}} \sim \overrightarrow{\mathrm{queen}} \end{align*}$

Distributional Compositional Semantic model

しかし、文章はただの単語の羅列ではなく、その言語の文法に従った係り受け構造をもっています。この単語間のネットワークを量子回路で計算することが、今回紹介する量子自然言語処理モデル(Distributional Compositional Semantic model 参考文献[1,2,4])となります。

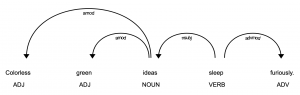
単語間のネットワークというのはどういったものでしょうか？簡単な例文から紹介します。

以下のダイアグラムは参考文献[4]からの引用となります。

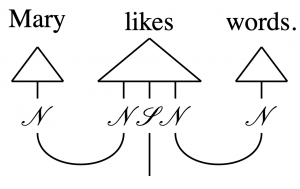
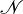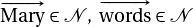ここでは主語 (Mary) と目的語 (word) を動詞 (like) が結合しする様子を表しています。ここで名詞である Mary と word は word embedding で利用したような word vector ( $\begin{align*} \mathcal{N} \end{align*}$ )の要素です。( $\begin{align*} \overrightarrow{\mathrm{Mary}} \in \mathcal{N}, \ \overrightarrow{\mathrm{words}} \in \mathcal{N} \end{align*}$ )

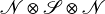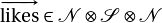一方で、主語と目的語を受け持つ他動詞である like は word vector のテンソル積 ( $\begin{align*} \mathcal{N} \otimes \mathcal{S} \otimes \mathcal{N} \end{align*}$ ) として表現されます。( $\begin{align*} \overrightarrow{\mathrm{likes}} \in \mathcal{N} \otimes \mathcal{S} \otimes \mathcal{N} \end{align*}$ )

ここで $\begin{align*} \mathcal{S} \end{align*}$ は、”文章の意味”のword vector に相当します。上記のダイアグラムで線がつながるところは同じindexを足し合わせる計算(テンソルの縮約、一部の業界では「テンソルの足を潰す」という)に対応しており、この文章の意味ベクトルは次の計算で得られます。

$\begin{align*} \sum_{i,k} [\mathrm{Mary}]_i [\mathrm{likes}]_{ijk} [\mathrm{words}]_k \end{align*}$
具体的な応用の一つが文章の分類です。以下の例では、まず、”kids play football”という文章の意味ベクトルを計算します。

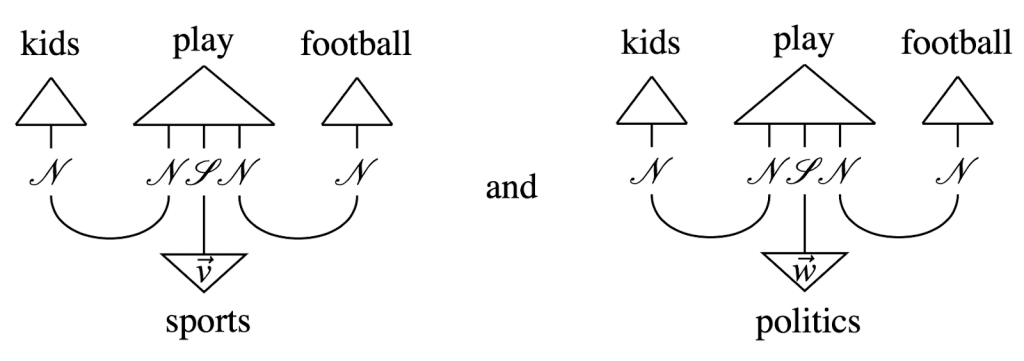
それとsports または politics という word vector との内積をスコアとして、この文章は sports に関係しているといったクラス分けができます。ただし、このテンソル・ネットワークの計算には、文章が複雑になるほど必要なメモリーや計算コストが増えるという問題があります。

前回のBlogで紹介したように量子ビット(qubit)は、0 と 1 の(量子)重ね合わせ状態を持てます。そのため、n-qubitあれば、2^n の古典 bit に相当します。また、文章の分類において、類似した意味ベクトルを探索する必要があります。この最近接ベクトル探索アルゴリズムにおいて量子アルゴリズムが効率的であることがこの論文[4]では示されています。

しかし、最初に提案された手法では、Quantum Random Access Memory (QRAM)の利用が前提となっている問題があります。しかし、量子重ね合わせ状態を実験で維持できるのは極短時間で、QRAMは今日でも未だ開発されていません。

この課題を解決し、現在でも利用できるNISQデバイスで実行できるように改良されたものがこれから紹介するDisCoCat model [5] です。このモデルでは、文章を現在のNISQデバイスで実行可能な量子回路に変換します。その際に入力となる単語については、ある種の量子回路に特定のパラメータを与えることで表現します。具体的にどのようなモデルかについて、公開されているモデルの実装などを紹介しながら以下では解説します。

DisCoPyによる量子自然言語処理の紹介

さて、今回のデモの実行に際しては、Oxford Quantum Group の開発しているDisCoPy (Distributional Compositional Python) という python library を利用します。文章を解析し、pytket により量子回路へ変換、そして前回にも紹介した qiskit library によって量子計算を実行します。discopy の github にある実装コードを補足しつつ解説します。https://github.com/oxford-quantum-group/discopy/tree/master/notebooks

なお、実行に際してはGoogle Colaboratory を利用しました。なお実行するためにdiscopy, qiskit, pytket, pytket-qiskit, noisyopt の library をあらかじめ、pip でインストールする必要があります。

さて、具体的にモデルを作成するまでに準備として以下のステップが必要となりますので順を追って解説します。

Vocabulary の定義
単語から文章の作成
単語の量子回路の作成
文章を量子回路へ変換

Vocabulary の定義

まず、今回のモデルで利用する語彙を以下のように準備します。

from discopy import Ty, Word

s, n = Ty('s'), Ty('n')
Alice = Word('Alice', n)
loves = Word('loves', n.r @ s @ n.l)
Bob = Word('Bob', n)
who = Word('who', n.r @ n @ s.l @ n)
is_rich = Word('is rich', n.r @ s)
vocab = [Alice, loves, Bob, who, is_rich]

ここでは型(Ty)と単語(Word)を定義しています。単語の定義の際に、型と他の単語とつながる際に右・左のどちらにつくかもテンソル積の形で与えます。具体的な単語の構造は以下のように可視化できます。

Alice.draw(fontsize=18, figsize=(1,1))
loves.draw(fontsize=18, figsize=(4,1))
Bob.draw(fontsize=18, figsize=(1,1))

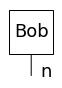
単語から文章の作成

さて、これだけではただ単語が並んでいるだけです。単語のテンソル積に対して、縮約を取る演算(Cup)や恒等変換(Id)などを順々に作用することで文章のダイアグラムを作ります。

from discopy import Id, Cup, pregroup

sentence = (
    Alice @ loves @ Bob
    >> Cup(n, n.r) @ Id(s) @ Cup(n.l, n)
)
pregroup.draw(sentence, fontsize=18, draw_types=True)

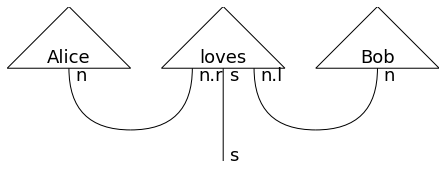
Aliceから伸びる線(n)とlovesの左の線(n.r)、lovesの右の線(n.l)とBobから伸びる線(n)が繋がったことが分かります。

より長いセンテンスも単語間のネットワーク構造を順々につなげることで作れます。

sentence = (
    Alice @ who @ loves @ Bob @ is_rich
    >> Cup(n, n.r) @ Id(n) @ Id(s.l) @ Cup(n, n.r) @ Id(s) @ Cup(n.l, n) @ Id(n.r) @ Id(s)
    >> Id(n) @ Cup(s.l, s) @ Id(n.r) @ Id(s)
    >> Cup(n, n.r) @ Id(s)
)

pregroup.draw(sentence, fontsize=24, figsize=(12, 8), draw_types=True

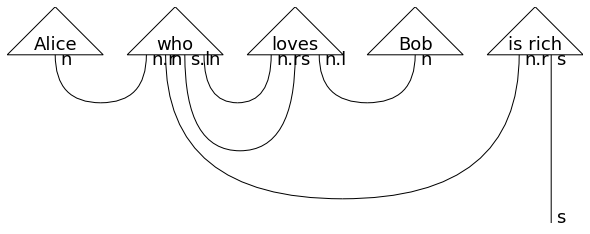
文章のダイアグラムを逐次コードで記述することは大変なので、サンプル・コードにならっていくつかの文章を自動生成します。

from time import time
from discopy.pregroup import brute_force

gen, n_sentences = brute_force(*vocab), 10
sentences, parsing = list(), dict()

print("Brute force search for grammatical sentences:")

start = time()
for i in range(n_sentences):
    diagram = next(gen)
    sentence = ' '.join(str(w)
        for w in diagram.boxes if isinstance(w, Word)) + '.'
    sentences.append(sentence)
    parsing.update({sentence: diagram})
    print(sentence)

print("\n{:.2f} seconds to generate {} sentences.".format(time() - start, n_sentences))
# Brute force search for grammatical sentences:
# Alice is rich.
# Bob is rich.
# Alice loves Alice.
# Alice loves Bob.
# Bob loves Alice.
# Bob loves Bob.
# Alice who is rich is rich.
# Bob who is rich is rich.
# Alice who loves Alice is rich.
# Alice who loves Bob is rich.

単語の量子回路の作成

次にdiscopyの circuit moduleを使って、これらの単語に対応する量子回路を作ってみます。まず、discopy での量子回路の作り方の例は以下のようになります。

from discopy.circuit import Circuit, sqrt, Ket, H, Rx, CX, SWAP

Bell = (
    Ket(0, 0)
    >> H @ Circuit.id(1)
    >> CX
)

print(Bell.eval().array)
# >> [[0.70710677 0.        ]
#     [0.         0.70710677]]

Bell.draw(fontsize=18, aspect='auto', figsize=(4, 2))

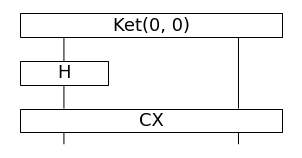
Bell state 生成回路

この回路は、Ketにより0に初期化した２つのqubitの状態(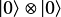 $\begin{align*} |0\rangle \otimes |0\rangle \end{align*}$ )を用意して、アダマール・ゲート( $\begin{align*} H|0\rangle = \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle),\quad H|1\rangle = \frac{1}{\sqrt{2}} (|0\rangle - |1 \rangle) \end{align*}$ )とControl NOT (CX, CNOT、これはcontrol bit (左)が１のときにtarget bit (右) を反転させる)を作用します。これは２つの entangle した qubit を作成する最も簡単なもので、具体的には以下のような計算となります。そして、実際に回路の測定(Bell.eval())をしてみると期待される結果が出力されます。

$\begin{align*} |0\rangle \otimes | 0\rangle \rightarrow \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle) = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} \end{align*}$

さて、先程定義した語彙に対応する量子回路をこれから作成します。まず、動詞(loves, is_rich)です。自動詞(intransitive verb)は、1 qubit の回路で以下のように仮定します。

def intransitive_ansatz(phase):
    return Ket(0) >> Rx(phase)

is_rich_circuit = intransitive_ansatz(r'$\theta$')
is_rich_circuit.draw(fontsize=18, aspect='auto', figsize=(2, 4))

自動詞の量子回路

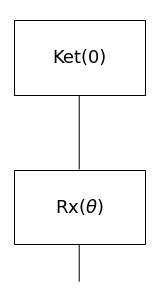
このRxゲートはqubitをX軸回りに回転(θ)させる操作で、動詞の意味を特徴付けるパラメータです。同様に、他動詞(transitive verb)は、主語と目的語の２つの入力を受けますので以下のように構築します。自動詞と同様に Rxゲートのパラメータで特徴づけ、更にもう一方の qubitにアダマール・ゲートを作用させて CNOT を作用することで、２つの qubit を entangle させます。

def transitive_ansatz(phase):
    return sqrt(2) @ Ket(0, 0) >> H @ Rx(phase) >> CX

loves_circuit = transitive_ansatz(r'$\theta$')
loves_circuit.draw(fontsize=18, aspect='auto')

他動詞の量子回路

あとは、関係代名詞(who)に対応する回路を作ります。ｗho は３つのqubitをentangleさせる回路で作成します。

GHZ = (
    sqrt(2) @ Ket(0, 0, 0)
    >> Circuit.id(1) @ H @ Circuit.id(1)
    >> Circuit.id(1) @ CX
    >> SWAP @ Circuit.id(1) # CNOTは左がcontrol bitのためswap
    >> CX @ Circuit.id(1)
)

GHZ.draw(aspect='auto', fontsize=18)

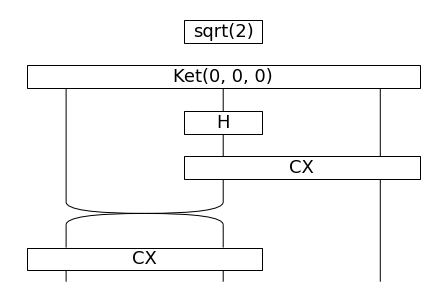
関係代名詞(who)の回路

ここでは、GHZ(Greenberger-Horne-Zeilinger) state $\begin{align*} |0\rangle \otimes | 0\rangle \otimes |0\rangle \rightarrow \frac{1}{\sqrt{2}} (|000\rangle + |111\rangle) \end{align*}$

を構成する回路を作成しました。

文章から量子回路への変換

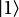さて、準備に手間が掛かりましたが、これから文章を量子回路へ変換していきます。CircuitFunctor により、文章に含まれる単語をそれぞれ対応する回路へと置き換えます。ここでは、名詞であるAlice, Bob に対応する状態は単純に qubit の $\begin{align*} |0\rangle \end{align*}$ と $\begin{align*} |1\rangle \end{align*}$ を対応させます。

import numpy as np
from discopy import CircuitFunctor

F = lambda params: CircuitFunctor(
    ob = {s: 0, n: 1},
    ar={Alice: Ket(0),
        loves: transitive_ansatz(params[0]),
        Bob: Ket(1),
        who: GHZ,
        is_rich: intransitive_ansatz(params[1])}
)

例

circuit = F([r'$\theta_0$', r'$\theta_1$'])(parsing['Alice is rich.'])
circuit.draw(fontsize=18, aspect='auto')

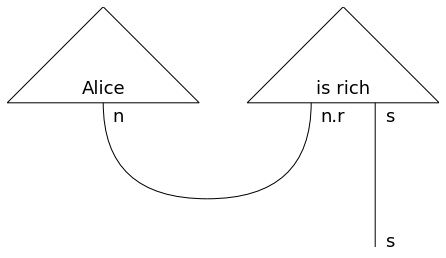
元の”Alice is rich”のダイアグラム

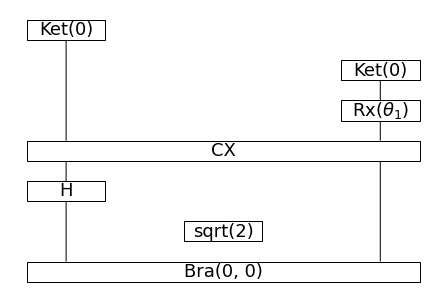
量子回路で表現した”Alice is rich”

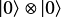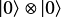量子回路の左側のKetが Alice の入力、右側のKet、Rxが is rich に対応しています。その先のCNOT以下の部分は、２つの単語からでる線を結合させる回路になっています。これは元のダイアグラムで単語から出る線がつながることを意味しています。この量子回路 $\begin{align*} C(\theta) \end{align*}$ を実行すると、入力されたqubit $\begin{align*} |0\rangle \otimes |0\rangle \end{align*}$ に対して、出力が $\begin{align*} |0\rangle \otimes |0\rangle \end{align*}$ となる確率

$\begin{align*} 0 \leq |C(\theta)|^2 \leq 1 \end{align*}$
が求められます。あるパラメータでこの回路を計算してみると以下のような数値が出力されます。

circuit = F([0.5, 1.0])(parsing['Alice is rich.'])
print(circuit.eval().array)
# >> (0.99999994+8.742278e-08j)

今回のタスクでは、この絶対値の２乗 $\begin{align*} |C(\theta)|^2 \end{align*}$ を文章が正しい確率と解釈し教師データを元にパラメータの学習を行います。

モデルの学習と実行

前置きが長くなりましたが、量子回路の実行では、同じくCambridge Quantum Computing のpytketを使ってQiskitで実行可能な形式に変換します。pytketというのは t|ket> という量子ゲート回路を効率的化するツールのwrapperになっています。

まず、ある初期パラメータで量子回路の計算を実行します。ここではQiskitのAerBackendを利用した量子コンピュータの数値シミュレーションでの実行ですが、実機(IBMQ)での計算も可能です。この結果から、各文章に対して真偽のlabelのセットである教師データを作成します。

from pytket.backends.ibm import AerBackend
from discopy.tk_interface import tensor_from_counts

def evaluate(params, sentences, backend=AerBackend(), n_shots=2**10, seed=42):
    circuits = [F(params)(parsing[s]).to_tk().measure_all() for s in sentences]
    _ = [backend.compile_circuit(c) for c in circuits]
    backend.process_circuits(circuits, n_shots=n_shots, seed=seed)
    return [tensor_from_counts(
        backend.get_counts(c, n_shots=n_shots),
        c.post_selection, c.scalar).array for c in circuits]

params0 = np.array([0.5, 1.0])
corpus = dict(zip(sentences,
        evaluate(params0, sentences, backend=AerBackend())))

これらの教師データで真偽は以下の通りです。

delta = .1
print("True sentences:\n{}\n".format('\n'.join("{} ({:.3f})".format(sentence, scalar)
    for sentence, scalar in corpus.items() if scalar > .5 + delta)))
print("False sentences:\n{}\n".format('\n'.join("{} ({:.3f})".format(sentence, scalar)
    for sentence, scalar in corpus.items() if scalar < .5 - delta)))
print("Maybe sentences:\n{}".format('\n'.join("{} ({:.3f})".format(sentence, scalar)
    for sentence, scalar in corpus.items() if .5 - delta <= scalar <= .5 + delta)))

True sentences:
Alice is rich. (0.979)
Alice loves Bob. (0.930)
Bob loves Alice. (1.016)
Alice who is rich is rich. (1.016)
Alice who loves Bob is rich. (0.937)

False sentences:
Bob is rich. (0.000)
Alice loves Alice. (0.000)
Bob loves Bob. (0.000)
Bob who is rich is rich. (0.000)
Alice who loves Alice is rich. (0.000)

Maybe sentences:

次に訓練データとテストデータに分割します。

from sklearn.model_selection import train_test_split

sentence_train, sentence_test = train_test_split(sentences, test_size=0.5,
                                            random_state=237)

print("Training set:\n{}\n".format('\n'.join(sentence_train)))
print("Testing set:\n{}".format('\n'.join(map(str, sentence_test))))

Training set:
Alice who is rich is rich.
Bob is rich.
Alice is rich.
Alice loves Bob.
Alice loves Alice.

Testing set:
Bob loves Bob.
Alice who loves Alice is rich.
Bob loves Alice.
Alice who loves Bob is rich.
Bob who is rich is rich.

これを量子回路のパラメータを学習させ正しく文章の２値分類ができるか検証します。

import numpy as np

def loss(params, sentences=sentence_train):
    return - np.mean(np.array([
        (corpus[sentence] - scalar) ** 2
        for sentence, scalar in zip(sentences, evaluate(params, sentences))]))

誤差関数は、量子回路を実行した結果と、正解ラベルの誤差で評価します。

そして、一旦、パラメータをランダムに初期化した後に、noisyopt library を利用して誤差関数を最小化するように回路のパラメータを最適化します。

from random import random, seed; seed(337)
params = np.array([random(), random()])

from time import time
import noisyopt

i, start = 0, time()

def callback(params):
    global i
    i += 1
    print("Epoch {} ({:.0f} seconds since start): {}".format(i, time() - start, params))

result = noisyopt.minimizeSPSA(
    loss, params, paired=False, callback=callback, niter=10, a=2)

学習後のモデルに対し、訓練データで与えていなかった質問をしてみました。

print("Is Alice who loves Bob rich?")
print("Yes, she is."
      if evaluate(result.x, ['Alice who loves Bob is rich.'])[0] > .5 + delta
      else "No, she isn't.")

# Is Alice who loves Bob rich?
# Yes, she is.

と、このように訓練データで真のラベル付されていた”Alice is rich”と”Alice loves Bob”の２つの情報から正しく質問に答えられました。(最後は若干、狐につままれた感はありますが)

さいごに

さて今回、NISQデバイスを活用した量子自然言語処理について紹介しました。この例から判るように実行できるものは、非常に限られた語彙の特殊な問題に限られています。実際のところ、現在の量子コンピュータ技術はまだ黎明期で実用的なタスクへの応用がなかなかに厳しい段階にあります。先日にIBMが発表したロードマップによると2023年には1121 qubits まで実現される目標となっています[6](因数分解などのタスクをこなすにはこれでも不十分)。やはり将来のスケール・アップが実用的な量子コンピュータの応用には不可欠です。それまでは、量子コンピュータというバズワードに踊らされることなく[7]、正しい量子コンピュータ開発の現状を把握することが必要なのだと思います。

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。

参考資料

「英国ケンブリッジ・クオンタム・コンピューティング、世界で初めて量子自然言語処理における実証実験を実施」ZDNet Japan 2020/4/20, https://japan.zdnet.com/release/30436981/
Quantum Natural Language Processing, https://medium.com/cambridge-quantum-computing/quantum-natural-language-processing-748d6f27b31d
“Mathematical Foundations for a Compositional Distributional Model of Meaning”, https://arxiv.org/abs/1003.4394
“Quantum Algorithms for Compositional Natural Language Processing”, https://arxiv.org/abs/1608.01406
“Quantum Natural Language Processing on Near-Term Quantum Computers”, https://arxiv.org/abs/2005.04147
“IBM’s Roadmap For Scaling Quantum Technology”, https://www.ibm.com/blogs/research/2020/09/ibm-quantum-roadmap/
“踊るバズワード〜Behind the Buzzword 量子コンピュータ”, https://eetimes.jp/ee/series/18963/