2023.04.07
ABテストを正しく評価するには?
みなさんこんにちは、グループ研究開発本部 AI研究開発室のK.Fです。
私は、現在、モバイルアプリを運営するグループ会社でデータサイエンティストとして、日々、データ分析観点に基づいた施策立案や、ABテストの効果測定のための統計検定、施策の効果の事前見積もり、KPI整理と可視化、データ分析基盤構築など幅広くデータ分析業務に携わっています。
今回は、その中でも、ABテストの効果検証についてお話しようと思います。
ABテストは、ビジネスの現場において、非常に知名度が高いものの、正しく実験を設計し正しく評価するのにはそれなりに考えるべきことがあり、専門知識を必要とします。そこで、今回は、ABテスト実施の際に気をつけているポイントと統計的解析の手法を、実務観点から数値検証を交えてご紹介します。
1. ABテストで気をつけているポイント
すでに、「ABテストの際に実務で気をつけている尖った観点だけ集めてみた」という過去の記事で、
- 複数の直行したABテストを行う
- トリガー条件を用いて分析感度を向上させる
- 長期効果を測定する
の3点についてご紹介済みですので、今回はそれ以外の観点をご説明します。(ぜひこの記事を読み進める前に、過去記事をご一読ください。)
① SRMが発生しないようにトリガー条件を設定する
上記の記事で、トリガー条件を設定し実験ユーザの絞り込みを行うことで、分析感度を向上させることができるという説明がありましたが、トリガー条件の設定には施策によって少し工夫が必要です。
例えば、多くのABテストでは、事前にテスト対象の変更を適用しないユーザ(control群)と変更を適応するユーザ(treat群)が、control:treat = 50:50の比率になるように、実験を設定します。しかし、実際にユーザー数を集計してみると、40:50のように期待通りの比率にならず、想定していた効果を優位に確認できない、もしくは期待と逆の効果を優位に観測するということが発生します。このことをSample Ratio Mismatch(SRM)といいます。SRMについては、[1]に非常に詳しくまとめられているので、ご参照ください。
では、どのようにトリガー条件を設定すればよいのでしょうか?
例えば、プッシュ通知を含む施策をテストした場合、アプリを開いたユーザをトリガー条件にし分析をすると、control群のユーザよりもtreat群のユーザが優位に多いという現象が発生する可能性があります。その場合は、過去のバージョンでアプリを開いたログがあるユーザなどに設定することで、SRMを防ぐことができそうです。
② 指標ごとに集計期間を変えて評価する
施策の効果は、メインKPI指標とサブKPI指標の両方をレポートするようにしています。
1. 実験経過日:実験が開始してから○日経過後のログを集計する
実験開始日以降にトリガーされたユーザのユーザのログを対象に集計します。◯日経過後のログには、実験初日にトリガーされたユーザも実験◯日目にトリガーされたユーザのどちらも含まれるため、期間を伸ばせば伸ばすほど、ユーザ数Nが増えます。一方で、前述の通り複数種類のユーザが混在するため、効果量の分散が大きくなり、信頼区間が広がってしまうかもしれないという側面もあります。
2. トリガー経過日:トリガーされてから○日経過後のログを集計する
トリガーされたユーザの○日後の振る舞いを評価します。トリガー経過日を揃えることで、効果量の分散が抑えれて信頼区間は狭まりますが、期間を伸ばしていくにつれて、対象のユーザ数Nが減っていくため、信頼区間が広がっていく側面もあります。また、トリガー経過後◯日を揃えることで、施策ごとの効果量の横比較をしやすいというメリットもあります。
3. トリガー経過日累積:トリガーされてから○日間のログを累計集計する
トリガーされたユーザの○日間のログを累計指標として集計します。例えば、「アンインストール」や「通知拒否の設定」などのネガティブなアクションは、テスト期間において一度でも発生すると良くないので、累計指標として集計することで評価します。
③「回数」と「確率」の2指標を集計する
ログを集計する際は、ユーザごとにイベントが発生した「回数」と、トリガーされたユーザ中イベントが発生したユーザの「割合 = 確率」の2種類の指標を作成することができます。例えば、ユーザがどれだけアクティブになるかを測定する場合、機能を使うユーザがどれだけ増やたかを評価したいならが「ユーザがアクティブになった確率(アクティブ率)」を利用しますし、売上につながるアクションがどれだけ増えたか評価したいなら「ユーザがアクティブとなる行動を起こした回数(アクティブ回数)」を利用します。
④ 外れ値を除去する
上記で説明したログを回数で集計する場合は、ほんの一部の上位ユーザの影響を大きく受け、平均値が引っ張られることがあります。そのため、上位を一定割合取り除くように外れ値処理をするようにしています。
2.効果測定
「頻度論的統計」に基づく効果検証の手法をご紹介します。統計手法の詳細には、書籍[2]や解説サイト[3]が世の中にはたくさんあるので、この章では、実装方法をメインで解説していきます。
① 母平均の差の検定: t検定
ユーザごとにイベントが発生した「回数」の平均値の有意差を検定するには、t検定を用います。
scipy.statsを利用すれば、以下のように簡単に検定することができます。
"""
control: List[int]
treat: List[int]
"""
import scipy.stats as stats
t_value, p_value = stats.ttest_ind(
a=treat,
b=control,
equal_var=False,
)
p_valueが有意水準(例えば、5%の場合は0.05)を下回っている場合に、有意差ありとみなすことができます。一方で、有意差がないと検定結果が出た場合に、サンプルサイズが少ないため効果がないとなったのか、サンプルサイズは十分だが単純に効果がなかったのか?を確認するべきです。サンプルサイズが十分かは、信頼区間の幅を算出することで、確認可能です。
有意水準5%の場合、標本平均の信頼区間は、以下のように算出することができます。
"""
samples: List[int]
"""
num = len(samples)
mean = np.mean(samples)
var = np.var(samples, ddof=1)
intervals = stats.t.interval(
alpha=0.95,
df=num - 1,
loc=mean,
scale=np.sqrt(np.divide(var, num)),
)
② 母比率の差の検定: カイ二乗検定
ユーザごとにイベントが発生した「確率」の有意差を検定するには、カイ二乗検定を用います。
こちらも、scipy.statsを利用すれば、以下のように簡単に検定することができます。
z_value, p_value, _, _ = stats.chi2_contingency(
observed=np.matrix(
[
[np.sum(treat), len(treat) - np.sum(treat)],
[np.sum(control), len(control) - np.sum(control)],
]
),
correction=False,
)
カイ二乗検定は、統計量が正規分布に従うので、信頼区間は以下のように算出することができます。
num = len(samples)
mean = np.mean(samples)
var = np.var(samples, ddof=1)
intervals = stats.norm.interval(
alpha=0.95,
loc=mean,
scale=np.sqrt(np.divide(var, num))
)
③ 効果量
有意差ありの検定結果が出た場合は、効果量がどのくらいあったのかも合わせてレポートするようにしています。効果量は、さまざまな考え方がありますが、主に以下の3種類を利用しています。
最大観測効果
controlの平均を基準にして、treatとcontrolの平均値の差がどれくらいあるのかを「最大観測効果」として表します。以下のような実装になります。
max_effect_size = (treat_mean - control_mean) / control_mean
レポートの場合は、「有意差あり、(max_effect_size*100)%の効果あり」と報告します。
最小効果量
有意差が存在しない場合は、サンプルサイズが足りずに信頼区間が広がってしまっているのかを伝えるために、controlの平均値を基準にして、treatとcontrolの信頼区間の和がどれくらいあるのかを「最小効果量」として表します。「最大観測効果」が「最小効果量」を超えない場合は、有意差なしの結論となるため、直感的です。
min_effect_size = (control_interval + treat_interval) / control_mean
レポートの場合は、「有意差なし、±(min_effect_size*100)%以上の変化なし」と報告します。
標準効果量
施策ごとの効果量を横比較したい要望があり、その場合は「標準効果量」を利用します。
t検定の効果量は、control/treatの平均値がどれだけ離れているかを表す「cohen’s d」を用います。(詳細な数式は、こちらをご確認ください。)
"""
control: List[int]
treat: List[int]
"""
# control
control_n = len(control)
control_mean = np.mean(control)
control_var = np.var(control, ddof=1)
# treat
treat_n = len(treat)
treat_mean = np.mean(treat)
treat_var = np.var(treat, ddof=1)
effect_size = np.divide(
np.abs(treat_mean - control_mean),
np.sqrt(np.divide(control_n * control_var + treat_n * treat_var, control_n + treat_n)),
)
カイ二乗検定の効果量は、control/treatの関連の強さを表す「\(\phi\)係数」を用います。(詳細な数式は、こちらをご確認ください。)
standard_effect_size = contingency.association(
observed=np.matrix(
[
[np.sum(treat), len(treat) - np.sum(treat)],
[np.sum(control), len(control) - np.sum(control)],
]
),
)
効果量の絶対値は、以下のような基準で効果があったのかを判断します。
| 検定 | 効果量の指標 | 効果量の目安 | ||
|---|---|---|---|---|
| 小 | 中 | 大 | ||
| t検定 | \(d\) | 0.20 | 0.50 | 0.80 |
| カイ二乗検定 | \(\phi\) | 0.10 | 0.30 | 0.50 |
より詳細な効果量は、[4]の表2によくまとめられています。
4. 数値検証
① t検定
テストデータを生成してみて、数値検証をしていきます。ユーザがあるアクティブイベントをどのくらい発生させたかの「アクティブ回数」を表す以下のような分布を作ってみます。
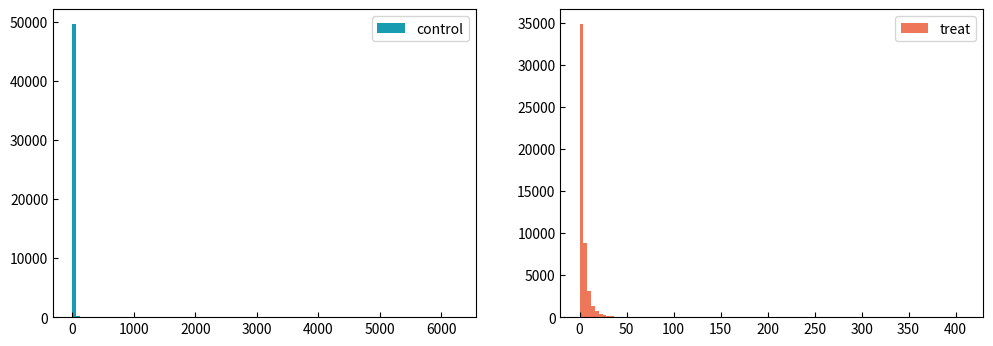
webサービスやモバイルアプリの解析をしていると、よく見る分布ではないでしょうか?
0や少しだけ使用するライト層が大半で、一部のヘビーユーザが横に広く存在するような分布です。このような分布をパレート分布といいます。以下のように簡単に生成することができます。
def generate_pareto_samples(
n: int, control_a: float = 2.0, treat_a: float = 3.0, effect_size: float = 1.05
) -> Tuple[List[float], List[float]]:
control = np.random.pareto(a=control_a, size=n)
treat = np.random.pareto(a=treat_a, size=n)
effect_size_factor = np.divide(np.mean(control), np.mean(treat)) * effect_size
return control, treat * effect_size_factor
このテストデータでは、controlを基準にしたtreatの効果量が+5%になるようにデータを生成しています。
次に、一部のヘビーユーザの影響を軽減するために、外れ値を算出して除外してみます。やり方は、以下のように○分位数を算出して、その値以上の値をフィルターアウトします。
"""
TH_OUTLIER_RATIO: float 外れ値の割合 1%の場合 0.01
"""
def trim_outliers(samples: List[int]):
th_outlier = np.quantile(samples, 1 - TH_OUTLIER_RATIO)
return list(filter(lambda x: x <= th_outlier, samples))
そうすると以下のような分布になります。
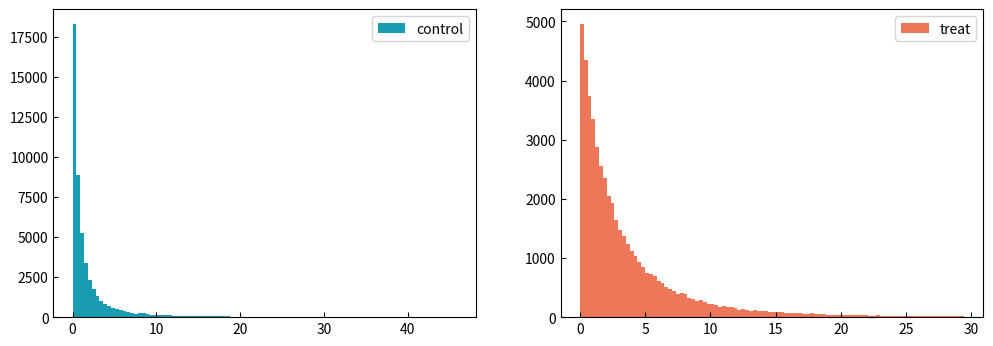
外れ値除去前と除去後の統計量をみてみると、違いが一目瞭然です。
| 統計量 | 外れ値除去前 | 外れ値除去後 | ||
|---|---|---|---|---|
| control | treat | control | treat | |
| counts | 50,000 | 50,000 | 49,500 | 49,500 |
| mean | 3.93 | 4.13 | 2.24 | 3.67 |
| std | 44.4 | 7.01 | 4.55 | 4.40 |
| max | 6249.9 | 408.8 | 45.8 | 29.5 |
| 信頼区間の幅(上下の平均) | 0.389 | 0.0615 | 0.0401 | 0.0387 |
統計検定を行った結果は以下のとおりです。
| 検定指標 | 外れ値除去前 | 外れ値除去後 |
|---|---|---|
| t値 | 0.978 | 50.6 |
| p値 | 0.328 | 0.0 |
| 有意差 | ✕ | ◯ |
| 最小効果量 | 11.4% | 3.5% |
| 最大観測効果 | 5.0% | 64.2% |
外れ値除去前には、有意差が確認できなかったサンプルでも適切に外れ値処理をすることで、優位な差を確認することができました。
② カイ二乗検定
ユーザがあるアクティブイベントをどのくらい発生させたかの「アクティブ確率」を表す分布を生成します。
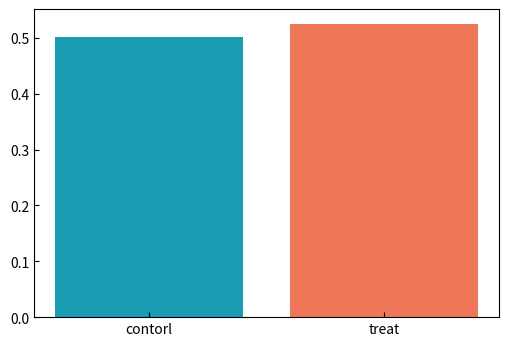
このような分布を「二項分布」といいます。以下のようなコードで簡単に生成することができます。
def generate_bernoulli_samples(n: int, p: float = 0.5, effect_size: float = 1.05) -> Tuple[List[float], List[float]]:
# control
control_size = np.random.binomial(n=n, p=p)
control = [1 if i <= control_size else 0 for i in range(n)]
np.random.shuffle(control)
# treat
treat_size = np.random.binomial(n=n, p=p * effect_size)
treat = [1 if i <=treat_size else 0 for i in range(n)]
np.random.shuffle(treat)
return control, treat
生成したサンプルデータの統計量は、以下のようになります。
| 統計量 | 効果量5% | 効果量2% | ||
|---|---|---|---|---|
| control | treat | control | treat | |
| counts | 50,000 | 50,000 | 50,000 | 50,000 |
| mean | 0.501 | 0.525 | 0.497 | 0.511 |
| std | 0.500 | 0.499 | 0.500 | 0.500 |
| 信頼区間の幅(上下の平均) | 0.0044 | 0.0044 | 0.0044 | 0.0044 |
検定結果は、
| 検定指標 | 効果量5% | 効果量2% |
|---|---|---|
| \( \chi^2 \)値 | 57.4 | 18.7 |
| p値 | 3.47e-14 | 1.56e-05 |
| 有意差 | ◯ | ◯ |
| 標準効果量 | 0.024 | 0.014 |
のようになり、効果量5%、2%ともに、有意差が確認できました。
4. まとめ
本記事では、ABテストの効果測定をする際に、気をつけるべき観点について実務に近いデータで数値検証を行いました。これから、ABテストの効果測定をしてみたいと考えている方には、参考になる内容になったかと思います。
次回は、今後チャレンジしたいと考えている「ベイズ統計」に基づいた効果測定(ベイジアンABテスト)が、実務においてどのくらい有効なのか?、「頻度論」とどのような違いがあるのか?などを検証していこうと思います。
最後に
グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集要項一覧からご応募をお願いします。 一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
参考
[1]. https://gingi99.hatenablog.com/entry/2019/08/09/212415
[2]. 参考になる書籍「A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実験とは」
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD





