2019.10.15

FXを機械学習(LSTM)で予測してみよう(テクニカル指標編)

こんにちは、次世代システム研究室のT.I.です．

今回は為替レートを機械学習で予測してみようという企画のPart 1です．まずは、為替データの特徴とその相場の読み方(?)を紹介したあとにPart 2 で紹介しますON-LSTM (Ordered Neurons Long Short-Term Memory)を理解するため前座としてLSTMの基本について簡単に紹介したいと思います．また、Part 3 では画像認識で高い性能を示したConvolutional Network を応用したTCN (Temporal Convolutional Network)を紹介していただきます．

時系列データと為替相場

時系列データとは、文字通り、ある地点の気温、動物の個体数、店舗の売上などなど時々刻々と変化するデータです．これを分析し期待値と分散、将来どのように変化するのかを解析することが時系列分析の１つの目的となります．

今回のテーマである為替ですが、そもそも価格とはどのように決まるのでしょうか？原則となるのは需要と供給です．ドルを買いたい人が多ければドルの値段は上がりますし、売りたい人が多ければ値段は下がります．輸入した商品の代金支払のためにドルを買うといった実需もありますが、外為取引のその殆どは投機取引にあります．銀行や個人投資家など様々なプレイヤーが市場で取引を繰り返しているわけです．これらの膨大な売買取引により市場の流動性が保たれ、世界経済が回っているというわけです．

その例としてドル円の最近の値動きをみてみましょう（データは HistData.com より取得させていただきました）．皆さんよく目にしているように、為替レートはジグザグと一見でたらめに動いていますが、何か波があるようにも感じられます．一体どのような数理的な原理が背後にはあるのでしょうか？

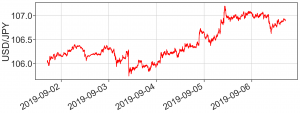
2019年9月第一週のドル円相場

有名なブラック・ショールズ・マートン理論では、為替や株価など原資産の複雑な値動きはブラウン運動としてモデル化します．この理論では、将来の価格そのものは判りませんが、変動の幅を確率的に予測できます．これにより、金融派生商品の価格を決定し、相場変動によるリスクを回避することができます．このブラウン運動とは液体中の微粒子(よく花粉と誤解されていますが違います)がジグザグに不規則に動くことで、正規分布する乱数の累積和で近似することができます．

次の図は、乱数で生成した偽物の為替変動です．一見すると最初に紹介したものとよく似ていますね、為替レートは本当にランダムに揺らぐだけなのでしょうか？

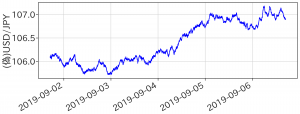
2019年9月第一週(?)の疑似為替レート

 

為替の動きそのもののでは判りにくいかと思いますので、単位時間当たりの値段の変化率である収益率(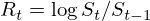\begin{align*} R_t = \log S_t/S_{t-1} \end{align*})で比較をしてみます．

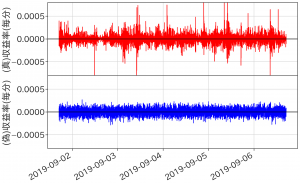
為替レートの収益率の時間変化

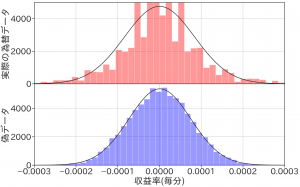
為替レートの収益率の分布

偽物のデータよりも実際の為替収益率は大きく揺らぎ、一定の時間帯に集中しています．また、ヒストグラムで見ても正規分布(黒線)から乖離し、正規分布から予想されるよりも大きな価格の変化が頻繁に起きていることがわかります．

このように為替変動は単純に揺らぐだけではない複雑な性質を持つようです．この相場をどう読み収益につなげるかがポイントとなります．その１つはファンダメンタルズ分析といって、ニュースや経済状況などから為替変動のトレンドを追うことです．実際に、経済政策や指標の発表前後で為替はしばしば大きく変動するため、売買のチャンスと言えます．

相場を流れを分析するもう１つのアプローチがテクニカル分析です．これは、過去の為替の動きから売り買いのタイミングを計る手法です．複雑な相場の流れを読むために多様な指標が考案されています．ここでは簡単にいくつかの指標について紹介します．

トレンド分析

  1. 移動平均線（Moving Average/MA）

直近の為替レートの平均値です．各時刻での揺らぎを滑らかにすることで、トレンドを読みやすくします．単純な平均移動平均ではなく直近の重みを強め、様々な種類があります．長期と短期の移動平均が交差するところがトレンドの転換点と言われています．

  1. Bollinger Band

移動平均線の上下に標準偏差のn倍の幅を付けたバンドのことです．為替の変化は１標準偏差以内なら約68%、２標準偏差以内でしたら約95%なので今後の値動きの参考になります．

  1. MACD (Moving Average Convergence and Divergence)

長期間の移動平均と短期間の移動平均の差です．更にMACDの移動平均をシグナルとして、MACDの交差点を売り買いのタイミングになるとされています．

オシレーター分析

  1. RSI (Relative Strength Index)

直近の「上昇平均÷（上昇平均＋下落平均）」で与えられます．相場の強弱を表す指標です．

  1. サイコロジカル・ライン

直近の価格が上昇した回数の割合です．上がり続けると次は下るのではという、投資家の心理を読む（？）指標と言われています．

ここで紹介したものの他にも多彩な指標が考案され利用されていますので調べてみると面白いですね．

今回紹介した指標を実際に計算してみますと以下のようになります．

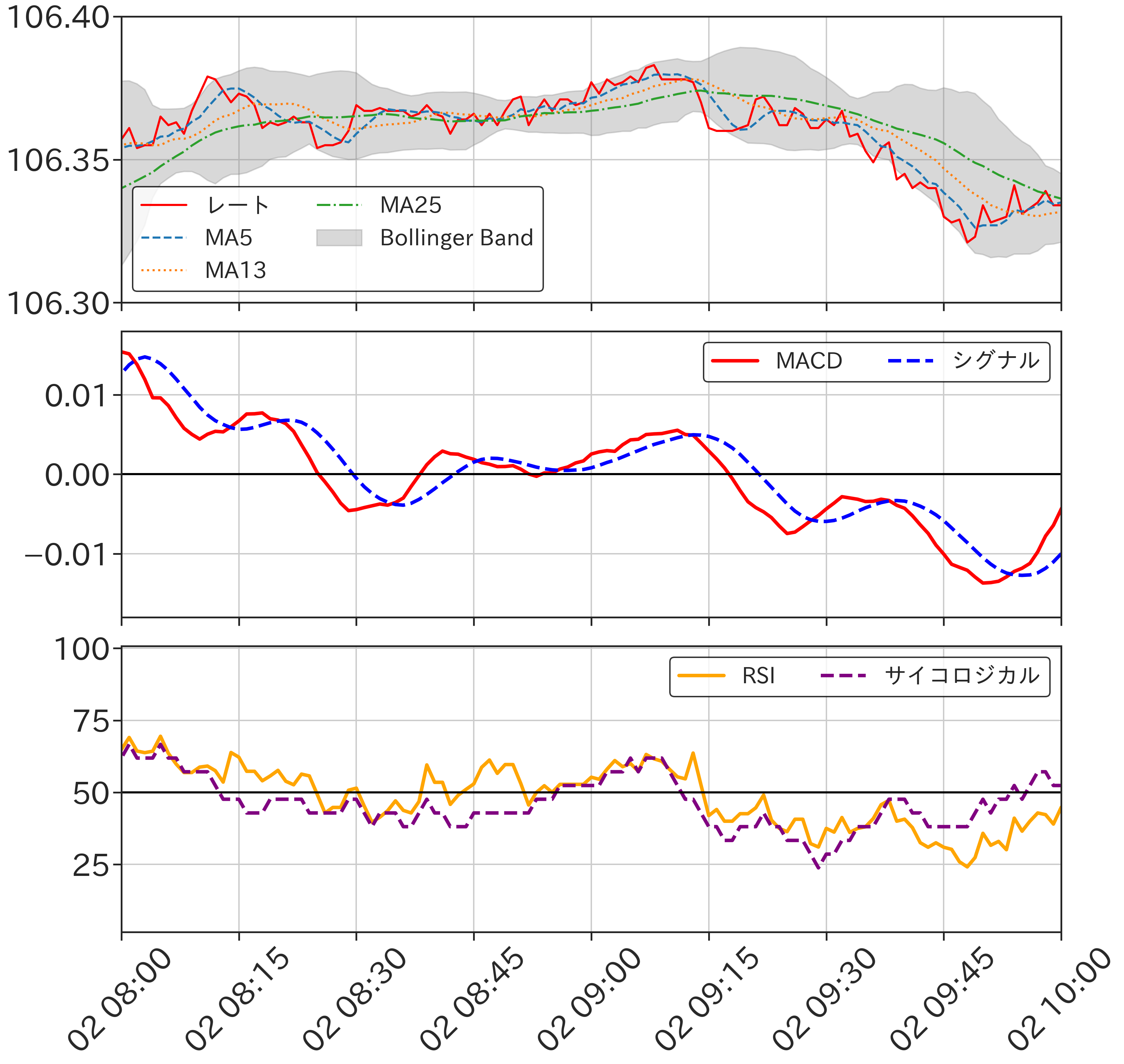
為替レートとテクニカル指標の例

 

ニューラル・ネットワークと時系列データへの応用

まず、ニューラル・ネットワークについて簡単に振り返ってみます．神経細胞（ニューロン）は他のニューロンからシグナルを受信し、閾値を超えると発火し、次のニューロンへとシグナルを伝えます．この機能を数理モデルにすると以下のようになります．

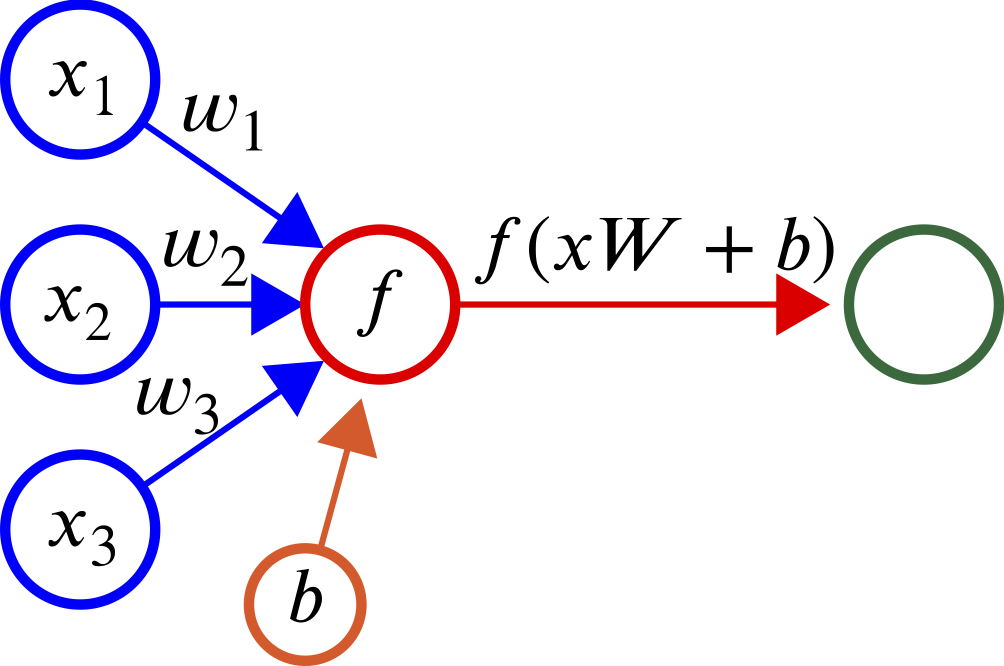
ニューラル・ネットワークの模式図

\begin{align*} h = f(xW + b) \end{align*}

ここで、x が入力信号、Wは重さ、b はバイアスといって入力に関わらず加わる信号です、これを活性化関数 f に作用させて、出力 h が得られます。この活性化関数には用途に合わせ様々なものがあり、代表的なものはsigmoid関数、tanh、ReLU(Rectified Linear Unit)などがあります． 下図はsigmoid関数とtanhを比較したものです．このように非線形の変換が加わることがこれから見るニューラル・ネットワークの肝となります．（ただの線形変換では何層も重ねる意味がありませんからね）

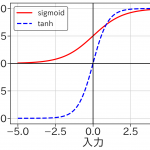
活性化関数の例

ニューラル・ネットワークはこれらのニューロンを何層にも重ねることで構成されます．次の例は入力層、中間層、出力層からなるネットワークを考えて、Iris(アヤメ)の種類を花弁・萼片の長さ・幅から予想するモデルです．

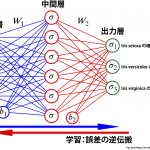
ニューラル・ネットワーク（アヤメの識別モデル）の例

 

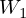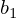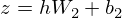まず入力\begin{align*} (x_1, x_2, x_3, x_4) \end{align*}に重み\begin{align*} W_1 \end{align*}とバイアス\begin{align*} b_1 \end{align*}が加わり中間層に伝わり、sigmoid関数を作用した結果(\begin{align*} h = \sigma(xW_1 + b_1) \end{align*})に更に重さを加えたもの(\begin{align*} z = hW_2 + b_2 \end{align*} )が出力層に伝わります．そしてsoftmax関数\begin{align*} \sigma(z)_i = \exp(z_i)/(\sum_{j=1}^K \exp(z_j)) \end{align*}を作用させた結果が最終的に得られる各々のアヤメやめの種類である確率です．softmax関数は次に紹介するON-LSTMの重要な要素でもあります．なお、今回のような全ての入力を受け取る層を全結合層と呼びます．

さて、このニューラル・ネットワークが正しく花の種類を分類できるようにパラメータを調整したいと思います．そのためには、予め答えの判っている学習データを用意して入力します．その出力結果と正解の誤差をネットワークの下流から逆に伝搬させパラメータの修正を繰り返し、ニューラル・ネットワークは正しく問題を学習することができます．

このような機械学習モデルはtensorflowを使えば以下のように簡単に作ることができます．また、参考となる学習データもsklearnやseabornなどのライブラリに沢山含まれていますので眺めるだけでも色々と面白いですね．

import tensorflow as tf
from sklearn import datasets
from sklearn.model_selection import train_test_split

# create nerual network
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Dense(6, input_dim=4, activation='sigmoid'))
model.add(tf.keras.layers.Dense(3, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

# load Iris data set & train
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model.fit(X_train, tf.keras.utils.to_categorical(y_train), epochs=200)

 

しかし、このような情報が一方的に流れるだけのネットワーク構造では、時系列データを予測するといった問題には適していません．過去の情報を再利用するように拡張されたネットワークをリカレント・ネットワークと呼びます。これは自分自身の出力結果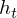\begin{align*} h_t \end{align*}を次の時刻の入力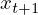\begin{align*} x_{t+1} \end{align*}と一緒に受け取ります．通常の入力と過去の出力結果に対する重みがあることに注意してください．これらが学習すべきパラメータになります．

\begin{align*} h_t = \tanh(h_{t-1} W_h + x_t W_x + b) \end{align*}

これをダイアグラムで表すと以下のようにRNNは横方向に展開して表現することもできます．

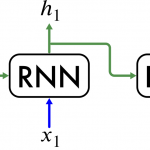
Recurrent Neural Network (RNN)の模式図

さて、ここでRNNの学習を考えます．先ほど紹介したように誤差の逆伝搬から各パラメータを正解データに近づけるように調整します．

しかし、長い文章・時系列データの情報を正しく学習するためには過去方向に教師データとの誤差を長時間伝える必要があります．単純なRNNでは、逆伝搬の誤差が発散したり消失したりする問題があります．この原因は、RNN では下流からの誤差に同じ重さWを何度も掛け合わせることに由来します．

この問題を回避するため考案された改良法の１つがLSTM(Long Short-Term Memory) になります．このLSTMでは隠れ状態 h だけでなくメモリー・セルという状態を加えることで、時系列データの情報をうまく処理することができます．

RNNよりも若干複雑にはなりますが、基本となるLSTM ユニットは以下のようになります．

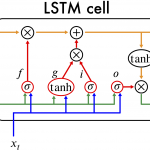
Long Short Term Memory (LSTM) cell の模式図

LSTMではsigmoid関数で活性化されるゲートが重要な役割を果たします．ゲート部分は基本的に以下のような式になります．\begin{align*} \sigma(x_t W_x + h_{t-1} W_h + b) \end{align*}

先ほどの図でみたようにsigmoid関数は０から１の数値であり、これらのゲートはメモリー・セルの情報をどの程度伝えるのか調整する役割を果たします．

さて、ここで、順番を追ってLSTM  cell を解説したいと思います．

まず、忘却ゲート (f)これは一つ前の記憶をどれだけ保持するかを決めるところです。次に、入力ゲート (i)で入力結果(g)の重要度を調整します．最後に出力ゲート(o)でメモリー・セルの情報を加えて出力します。LSTMユニットを数式で表現すると以下のようになります．

\begin{align*} f &= \sigma\left(x_t W_x^{(f)} + h_{t-1} W_h^{(f)} + b^{(f)} \right) \\ g &= \tanh\left(x_t W_x^{(g)} + h_{t-1} W_h^{(g)} + b^{(g)} \right) \\ i &= \sigma\left(x_t W_x^{(i)} + h_{t-1} W_h^{(i)} + b^{(i)} \right) \\ o &= \sigma\left(x_t W_x^{(o)} + h_{t-1} W_h^{(o)} + b^{(o)} \right) \\ c_t &= f \odot c_{t-1} + g \odot i \\ h_t &= o \odot \tanh(c_t) \end{align*}

一見すると複雑には見えますが、結局は、入力を４つの活性化関数にそれぞれ入力するだけであることがわかります．ここでは\begin{align*} \odot \end{align*} とは、行列の要素毎の掛け算です．LSTMでは、RNNと異なりメモリー・セルの逆伝搬では重み行列の掛け算はありませんから、逆伝搬での学習において問題が生じにくいように改良されています．

 

LSTMによる為替予測

最後になりましたが、LSTMを使って実際に為替を予測してみようと思います．今回のデータは2019年の1月から７月までの一分毎のドル円のデータを用い、GPUクラウド by GMOの１GPUプランを利用させていただき、コードの開発には Tensorflow を用いました．解析環境の詳細についてはPart 3で詳しく説明していただきます．

さて、この期間の為替変動は以下のようになります．このうち前半８０％のデータで学習し、残りの１０％ずつを学習結果の検証とテストに用いました．

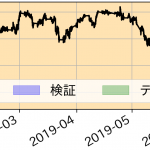
2019年1月から7月のドル円レートの変化

今回の課題では、過去６０分の情報から１分後のレートを予測したいと思います．機械学習のモデルとしては、LSTM(unit数は40)＋全結合層のみとする単純なモデルを用います．

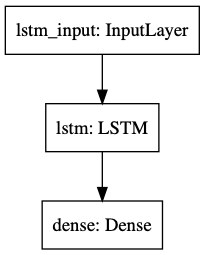
予測モデルの概略

入力する特徴量としては（１）為替レートのみのほかにも上で紹介したテクニカル指標について（２）トレンド系指標込み（３）オシレーター系指標込み（４）すべてのテクニカル指標込み、の４通りを検証してみました．

結果は以下のようになりました(週末部分はデータが欠損しているので注意してください)．レートのみでは、乖離が大きいですが、トレンド系指標を含めると予想結果がだいぶ改善されました、一方、今回の検証ではオシレーター系はあまり重要ではないような結果となりました．定量的にRMSE (Root Mean Square Error)を比較するとトレンド指標込みの予測は改善効果が大きいようです．

 

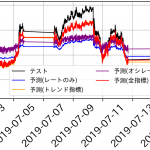
テクニカル指標込みでの為替予測結果

 

特徴量 RMSE
レートのみ 0.276
トレンド系 0.108
オシレーター系 0.303
両方 0.112

 

さて、一見うまくいったようにも思われますが、拡大して詳細に見てみましょう．トレンド指標込みでは結構、予測結果は頑張っているようですが、やはり無視できない程度の誤差は残っています．

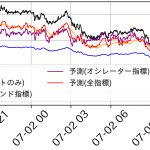
テクニカル指標込みの予測結果（拡大図）

さて、今回はこのような結果には終わりましたが、あくまで今回使用したモデル・データでの結論であって、LSTMやテクニカル指標の有効性について検証したものでないのでご注意ください．

次はLSTMを拡張したON-LSTMという最近話題の機械学習モデルについての解説をしていただきますので、もうしばらくお付き合いいただければと思います．導入で紹介したファンダメンタルズ分析という観点から、自然言語処理でニュースなどの情報を学習させて、トレンドを予想するということも面白いテーマかもしれませんね．

 

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。

 

  • Twitter
  • Facebook
  • はてなブックマークに追加

グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。

 
  • AI研究開発室
  • 大阪研究開発グループ

関連記事