ベイズ統計の評価基準をちゃんと勉強してみる1（イントロ編）

こんにちは。次世代システム研究室のベイズ大好きK.Nです。
いままでのブログではFXやらDNNやらを取り上げていたのですが、たまには基礎に立ち返ってみようということで、堅い感じのお題です。
内容的にすごく新しいわけでも、華やかな内容なわけでもないので、いまこの文章を読んでいる方は非常にマニアックですね。

さて、僕は統計や確率モデルを齧っていた影響で、問題解決のための考え方の基準がそこに拠っているなと感じます。同じ問題を解決する方法が複数あり得る中で、自信を持って選択できる基準を一つ以上持っていることは、意思決定を迅速にできるという点で非常に有利だと思うんですね。

ということで、この基盤をより強固にすべく、さらに知識をしっかり付けるために選んだ本が、渡辺澄夫先生の「ベイズ統計の理論と方法」（コロナ社）です。スキルアップ補助制度を使って購入しました。

この本の主題は、
「ベイズ推定は確率モデルを定義さえすれば（理論的には）最適解は出るけど、果たして定義したモデルは正しい（良い）のか？」
という問題に対する、ものさしを与えることです。
その過程で、それぞれのものさしが何を意味しているのかや、どんな特徴があってどう使っていいのか、というところを原理から追う形で書かれています。（とはいえ実際に理解するには非常に難解ですが…）

今回この本を読んでいて一番混乱してしまったのが、「ゴールはどこにあるのか」という点でした。一つ一つの数式が丁寧に書かれていて追いやすいようにできているのですが、追っているうちに、「なぜこの式を見ているんだっけ…」となるシーンが多かったんですね。それを踏まえてこのシリーズでは、あまり式を使わずにイメージをつかんでもらえるように書こうと思っています。ここで追うべきゴールまでざっくりとわかった上で本を読んで頂けると、理解を進めやすいと思います。

ベイズ推定について

そもそもベイズ推定ってなんだっけ？

「ベイズ推定って事前分布使うやつでしょ？」っていうイメージの方が多いと思います。その通りです。
もうちょっと細かく言うと、「データがパラメータに応じて確率的に得られるような条件付き確率を定義して、パラメータの事前分布を定義して、観測データを与えることで得られる事後分布を使ってなんやかんやするあれ」です。

今回の参考書では、事後分布と条件付き確率を使ってパラメータを積分消去することで得られる「予測分布」を作るところがベイズ推定と定義していますね。
（もう少し広い意味で、パラメータの点推定値として、事後分布の最大値や平均値を使うものもベイズ推定に含めていいと僕は思います。）

何が嬉しいの？

パラメータや予測値の確率分布が得られます。

と言って「だから何？」という方もいるかもしれませんが、点推定と分布推定はそもそも情報の量が違うので、できることも多くなりますね。
もちろん分布を使って点を推定することもできますし、「どのくらい当たった/外れた」の「どのくらい」を、確率を使って見積もることもできます。

天気を予測するとき、「晴れと予測したから傘はいらないな！」よりも「70%で晴れだけど、30%で雨だから念のために傘を持っていこう」とかできた方が便利ですよね。

他にも、「データはこうして作られるだろう」といった仮定を手軽に定式化できたりとか、幅広い問題に対応しやすい柔軟性があります。

柔軟すぎてライブラリ化しにくいのが悲しいところですね。

難しい点

自分の中にある「こうなっているだろう」を定式化できるのが嬉しいと先ほど書きましたが、一方でそれがない時にどうするか、という問題があります。ノイズは等分散のガウス分布でいいのか、いやノイズが入る前の値の絶対値が大きければノイズの分散も大きくなるんじゃないか、など、複雑にする方法はいくらでも思い付いてしまうわけです。
もちろん、観測されるデータには、「真の確率分布」というものが必ずあるはずなので、それを知り、使ってあげることができれば、良い推定が行えることは間違いありません。

こういった「どれを選べばいいの？」という問題を考える上で助けになる概念である、「情報量基準」を説明してくれているのが、この本ということになります。

余談ですが、「どうやって事後分布や予測分布を得るのか」というのも、ベイズ推定の難しさの一つです。この問題に対するアプローチとして、マルコフ連鎖モンテカルロ法や、変分ベイズ推定といった方法がありますが、モデルが複雑になるほど難易度や正確性は上がっていきます。

汎化損失

KL距離と汎化損失

真のモデルq(x)がわかっていると仮定して、予測モデルp(x)と真のモデルq(x)の距離を測りましょう。確率分布の距離としてよく使われる定義として、カルバック・ライブラ距離（KL距離）と呼ばれ、

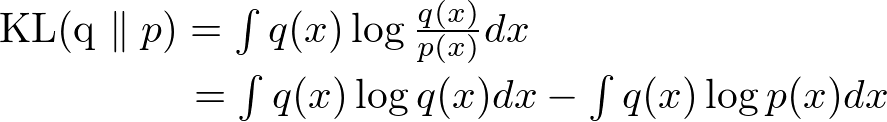
のように表されます。式からもわかる通り、p(x)がq(x)と等しいなら、距離は0になります。また、KL距離は非負です。
こうすると、右辺第一項は、q(x)の負のエントロピー、すなわち真の分布の複雑さ（単純さ？）を表します。真の分布は決まったものなので、定数ですね。
第二項は、予測分布の対数を真の分布で積分したものです。なんのこっちゃって感じなのですが、真の分布が大きい点は、予測分布も大きい方が嬉しいですよね。その嬉しさの感度みたいなものを対数で調整したものだと思えばいいと思います。で、その符号反転なので、ペナルティです。これを汎化損失と呼びます。

汎化損失が小さくなるような予測分布を作ることができれば、その予測分布は秦の分布に近い、ということです。
ただ、もちろん真の分布は未知なので、実際にこの量を計算することはできません。そこで、この本では、「計算可能な値を使って、いかに汎化損失を見積もるか」を追い求めていくことになります。

ただし、ここで言う「計算可能な値」とは、「既知の情報を組み合わせることで理論的には計算可能な値」という意味で、例えば「階層モデルにおいて事後分布や予測分布を実現するのは難しい」とかそういう点は考慮しないものとします。
もっとも、この本の後半ではそういったものを実現するためのテクニックについての説明もあるので、「実現できるもの」として扱うことは特に問題ないのですが。

計算可能な値

計算可能で、かつ汎化損失と関連が深い値を定義していきます。いずれも、予測モデルと観測サンプルから計算されるものです。つまり、観測されるサンプルのランダム性に応じて確率的に変動する値でもあります。

経験損失

経験損失は、各観測サンプルに対する予測分布の負の対数を平均したものです。つまり、真の確率モデルq(x)からの無限個のサンプルを集めた際の経験損失は、汎化損失と等価です。
別の言い方をすると、 観測サンプルに基づく汎化損失の実現値です。

自由エネルギー

自由エネルギーは、周辺尤度の負の対数に相当します。
周辺尤度とは、確率モデルとサンプルが与えられたとき、その二つの関連の強さ（観測されたサンプルを、確率モデルでどの程度再現できるか）を表します。その負の対数なので、再現の難しさのようなものを表しているとイメージすればよいと思います。
自由エネルギーは、サイズnのサンプル集合（{x1, x2, …, xn}）に対する真の同時分布と予測同時分布のKL距離に関連する値です。同サイズのサンプル集合を無限個用意し、それぞれの自由エネルギーの平均を取ることで、真のモデルのエントロピーとKL距離の和になります。
経験損失を、「観測サンプルに基づく汎化損失の実現値」と考えると、自由エネルギーは「ひとつの観測サンプル集合に基づく同時分布のKL距離の実現値」という言い方ができそうです。

ここまで

いかがでしたでしょうか？今回はベイズ統計のおさらいと、その評価を行う上での重要な概念である、汎化損失の話をしました。
次回は、参考書の流れに沿って、「事後分布が正規分布で近似できる場合の汎化損失の挙動」について直感的な解説していきたいと考えています。主な内容は、
・事後分布が正規分布で近似できるという仮定の嬉しさ
・この条件における汎化損失の挙動
・事後分布が正規分布で近似できるためには
といった流れで考えています。

引き続き、なるべく式を使わずに、直感的な説明で進めていきたいと思います。

 

最後に

次世代システム研究室では、多様なアプローチを持ち寄って議論を深め、より良いサービスを追い求めていける仲間を募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。