2021.07.08
エンジニアにこそ知ってほしい経済学〜オークション理論基礎編〜
こちらは【【ノーベル賞×実務】pythonで簡単配属分け【ゲーム理論】の続編シリーズとなっています。
次世代システム研究室のT.Sです。皆さん経済学って好きですか???エンジニアは理系卒の方も多く、文系科目である経済学にあまり馴染みがない方も多いのではないかと思います。ですので、好きか嫌いかと問われても「そもそも知らないよ・・・」という方も多いのではないでしょうか。しかし我々の周りでは経済学の知識を元に構築された仕組みなどが数多く存在しています。そこで今回はその一つであるオークション理論を紹介したいと思います
オークション理論とは
オークションというと何を思い浮かべますか?いわゆるクリスティーズ様のような美術品を扱う格式高いオークションハウスを想像される方もいらっしゃるかと思います。ただエンジニアという視点で考えるとそれ以外にも多くのオークションが存在しています。毎日目にするオークションとしてはオンライン広告がその代表例になるかと思います。何気なく表示されているオンライン広告ですが、裏ではRTB(Real-Time Bidding)と呼ばれるオークションが表示毎に行われています。
RTBの詳しい説明は割愛しますが、我々がWebサイトを参照した際に、その広告が載っているサイトの特性やオーディエンスデータを踏まえ入札が行われ、勝者の広告のみが表示されています。入札->勝者決定とまさにオークションそのものですね。このように我々の見えない場所でも数々のオークションが行われているわけです。
オークション理論とは、オークションを分析し、より効率的で期待収入の高い市場をデザインするための学問となります。上記で挙げたようにオンライン広告では、HeaderBiddingなど様々なオークション形態が採用されているため、オークション自体を知るオークション理論はエンジニアにとっても有益になるであろうという訳です。ちなみに1996年のヴィックリー氏や、2020年のミルグロム氏はオークション理論に対する貢献が認められたことによりノーベル経済学賞を受賞しております。ここからも近年でも非常に注目度が高い分野だというのがわかりますね。
よくあるオークションの形式
オークションと一言ではいいますが、具体的などのような形式があるのでしょうか?
これは本当に色々なケースがありますが、今回はそのうちオンライン広告で使われる代表的な2つをご紹介しましょう
1st price sealed-bid Auction
まず1つ目は1st price sealed-bid Auctionになります。一般的にはファーストプライスオークションなんて呼ばれるものですね。注目すべきは[1st price][sealed]という箇所になります。
まず先に[sealed]という点に注目しましょう。日本語でいうと「封印入札」と訳しますが、各入札者が入札額を厳封して主催者に提出する仕組みです。要は入札時に他の入札者の入札額がわからない状態で入札しなければならないと理解頂ければ齟齬はないかと思います
次に[1st price]という箇所になります。こちらも単純な話で「一番高い入札をした入札者が勝者となり、その入札額を支払う」という仕組みになります。どちらも非常に単純ルールであり、想像に難くないい仕組みかと思います。
2nd price sealed-bid Auction
次に2nd price sealed-bid Auctionをご紹介しましょう。変わったのは1stという文字列が2ndになっただけですね。
この[2nd price]という意味は「一番高い入札をした入札者が勝者となり、2番めに高い入札金額を支払う」という仕組みになります。ちょっとややこしいですね。簡単に図示すると以下のようになります。何故このような変わった仕組みを取るのか?というのはこの後開設いたします。

どちらのオークションが優れているのか
代表的な2つのオークション形式を紹介しましたが、オークション理論に照らし合わせるとどちらのオークションが優れているのでしょうか?今回は「耐戦略性」と「期待収入」の2つの視点で考えたいと思います。これらを考える際に、単純化して考えやすくするため以下の前提を置くことを留意ください。
- 1つの財のみを扱うオークションとする(単一財オークション)
- オークションに参加する人数は2人のみ
- それぞれの参加者の材の評価額は[0,1]の一様分布
耐戦略性観点でのオークション分析
耐戦略性とは、「自分の真の評価値以外の値を入札しても、絶対に得をしない」という意味になります。つまり、ある財において0.5円の評価をしていた場合に、それ以外の評価値で入札しても得をしないという意味になります。
ファーストプライスオークション
ファーストプライスオークションで、これが成立するか見てみましょう。
まず「得をする」という表現を定義してみましょう。オークション理論では、これを[自分の評価値]-[実際の入札額]で表現します。要はどれだけ安く変えたかですね。評価値そのもので落札した場合にはこのお得は0になりますし、評価値以上で落札すればマイナスとなってしまいます

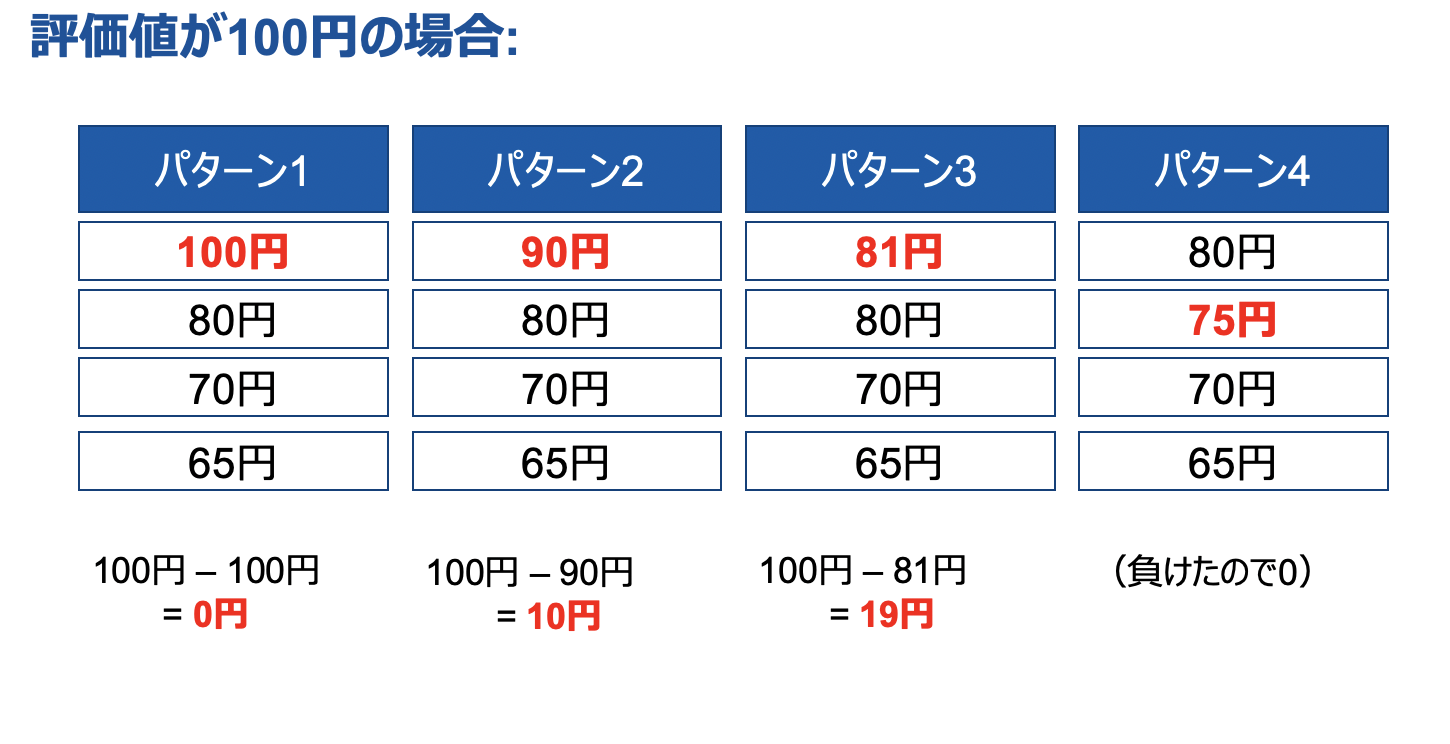
では入札額を変更した場合のお得(利得)を比較してみましょう。今回は評価値を100円、入札額を100,90,81,75の4パターンで表してみました。一見して分かる通り、入札額を戦略的に変更し81円にした場合が利得が最大となっています。つまり戦略を持って入札額を変更したほうがお得感は増すため耐戦略性は存在しないという事がわかります。当たり前と言えば当たり前ですね。ちなみにこの変更幅を研究するアルゴリズムとしてShading Algorithmという分野も存在しています。
セカンドプライスオークション
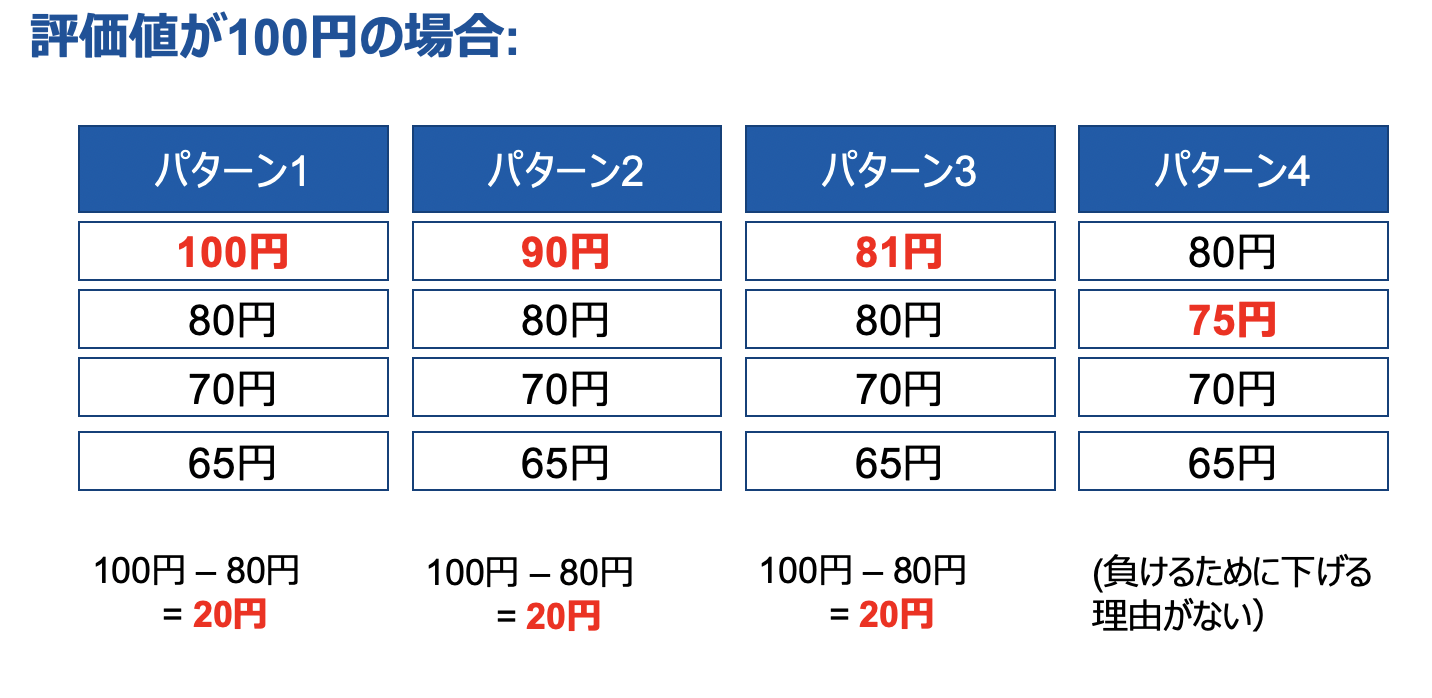
ではセカンドプライスオークションはどうでしょう?まず自分が勝者の場合を考えてみましょう。ファーストプライスでは自分入札額が評価値より減算されていたため、これを操作する理由がありました。しかし今回は2位の評価値が減算されているため、自分の評価値を下げる理由がありません。強いて言うなら「負ける」ためにはありますが、それであれば入札に参加する理由がありません。そのため自分の評価値を素直に申告することが最良の手段となっています。

次に自分が敗者の場合を考えてみましょう。この場合「勝者になる」ために入札額を操作する理由があります。しかし以下の式から分かる通り、勝者になるよう操作しても利得はマイナスとなり損をするため、こちらも操作する理由になりません。以上2つの理由により、セカンドプライスオークションでは自分の評価値を素直に入札することが最善手であり、耐戦略性が成立していると考えられれます。

以下ファーストプライスオークションでお見せした各パターンですが、それぞれの利得は同一であり、操作の必要がないことがこちらからもわかりますね
期待収入観点でのオークション分析
先述によりセカンドプライスオークションのみに耐戦略性が備わっていることがわかりました。耐戦略性という観点ではセカンドプライスの方が優れていると言ってよいでしょう。しかしセカンドプライスオークションを実施した場合に、売り手側が「儲からない」のであれば、これを採用する理由にはなりません。そこでファースト/セカンド双方でどれだけ期待収入が得られるかの観点でも比較してみましょう。
ファーストプライスオークションの戦略
先程の分析でセカンドプライスオークションは評価値をそのまま入札することがわかっていますが、ファーストプライスでは一定の割合で操作しなくてはいけません。そのためどの程度操作されるのかを利得関数を最大化することを目的として計算したいと思います。
まず操作の割合をkと置き、この数だけ評価値を割ることを戦略とします。前提として評価額は[0,1]なので、入札額は[0,1/k] となります。また入札額は一様分布であり、それがkだけ圧縮されているので、入札がx円以下になる確率はkxとなります。
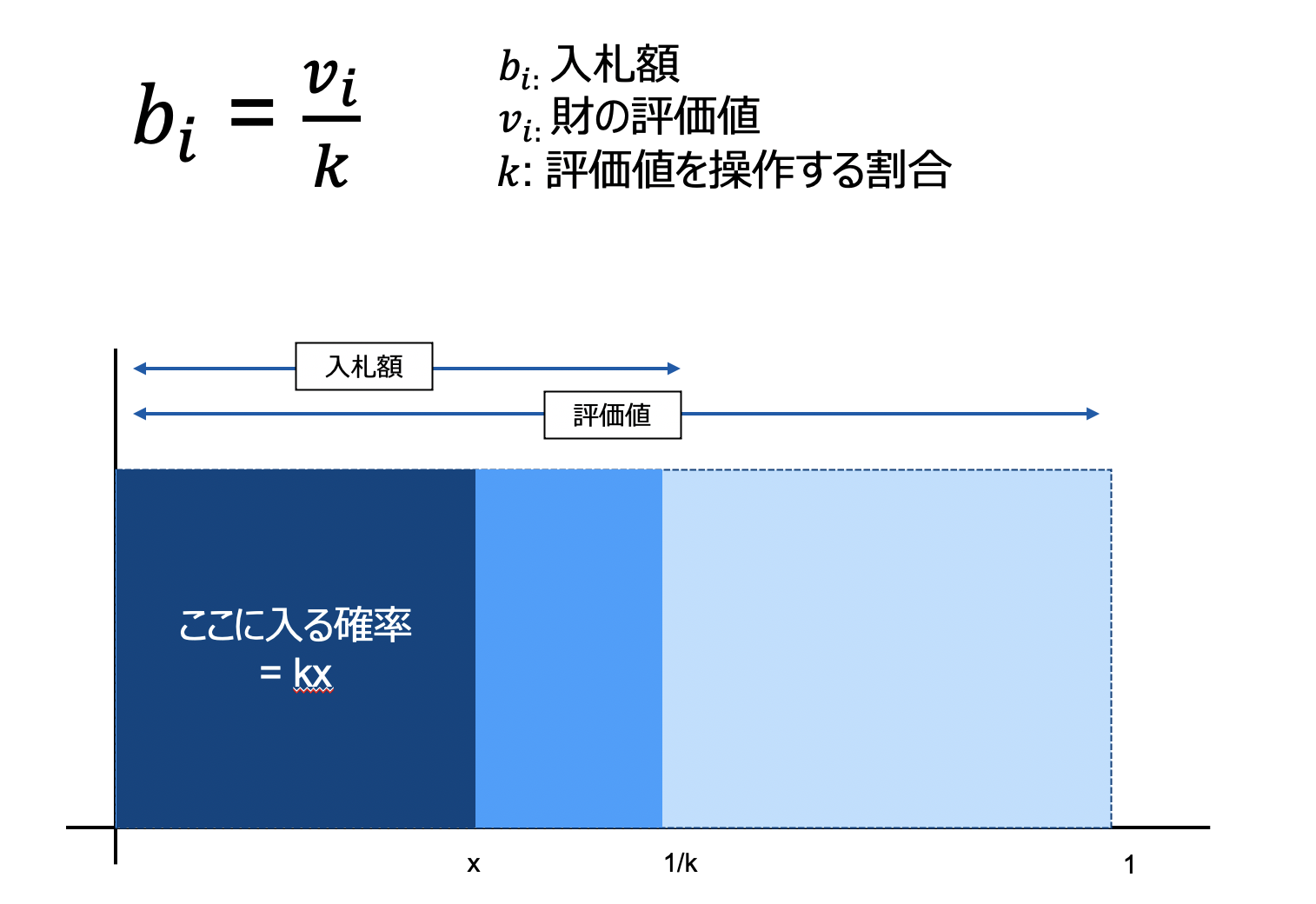
この式を利用して、b1が勝つための確率と利得を計算します。b1が勝つ確率を求めるということは b2 < b1 となる確率を求めるということになります。先で求めたkxという式を利用すると、これはkb1と合わすことができます。また利得はv1-b1で計算することができるため、これをかけ合わせるとb1の期待利得は以下のようになります。

入札者1として最も望ましいのは、この期待利得が最大となる場合です。これを求めるためにこの2次関数の1階条件を取ると、評価値を1/2することが最適だと求められます。これは入札者2でも全く同様となります。これにより評価値を1/2操作することがファーストプライスオークションで取りうる戦略だと考えることができます。

入札者が3人に増えた場合も計算すると以下のようになります。基本的な考え方は同じで、勝つための確率としてi-1人の同時確率分布に変えるだけですね。結果としての戦略は人数が増えるほど、Shading幅が小さくなっていくこととなります。これは参加者が多いのであれば、その分高い入札をしてないと勝てないであろうという直感とも等しい結果となっていますね。


ちなみに入札者がn人の場合は、(n-1)/nのShading幅を取るということなっています。これはベイジアンナッシュ均衡と呼ばれるゲーム理論の考え方で導出されているものです。あくまでこれはベイジアンナッシュ均衡の値であるため、この値をとれば誰しも最大の利得を得られるというわけではないことはご注意ください。
期待収入シミュレーション
ファーストプライスオークションの戦略が定義できたため、これを使って期待収入がそれぞれどの程度になるかシミュレーションしてみましょう。改めてそれぞれの入札価格は以下の通りとなります。
- オークションに参加する人数は2人のみ
- それぞれの参加者の材の評価額は[0,1]の一様分布
- ファーストプライスオークションでは、評価額に1/2を掛け入札額とする
- セカンドプライスオークションででは、評価額をそのまま入札額とする
さてこれをもとにシミュレーションコードを書いてみましょう。シミュレーションといっても難しいものではなく、ただ単に一様分布から評価額を取り出し、それを複数回実行するだけです。今回は1,000,000回実行してみました。コードは以下のようなもので、至極単純なものとなっています。
import random
def bids(bidder, coeff=1.0):
bid_list = []
for _ in range(bidder):
bid_list.append(random.uniform(0, 1) * coeff)
return bid_list
def kth_auction_gain(k, bidder, coeff=1.0, loop_n=1000000):
winner = []
for i in range(loop_n):
winner.append(sorted(bids(bidder, coeff), reverse=True)[k-1])
return sum(winner) / len(winner)
bidder = 2
BAYESIAN_NASH = (bidder-1) / bidder
print(f'1st Price: {kth_auction_gain(1, bidder, BAYESIAN_NASH)}')
print(f'2nd Price: {kth_auction_gain(2, bidder)}')
結果について皆さんはどのように想像しますでしょうか?Shadingされている分だけ1stが低くなるのか?それとも2位を取るため2ndが低くなるのか?いろいろ考えはあるかと思いますが結果は以下の通りとなります。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1st Price: 0.33353220066784744 2nd Price: 0.33299106994215494
1st/2ndほぼ同じ値となりました!!
これはどういうことなのでしょう?実は当条件において、1st/2ndの期待収入が同じ(1/3)になるということは「収入同値定理」と呼ばれ、既に理論的に証明されているものになっています。冒頭で1996年にヴィックリー氏がノーベル経済学賞を受賞したということを記載いたしましたが、受賞理由はこの「収入同値定理」の理論的証明によるものになっています。
上記を踏まえ、この2つのオークション形式を比較すると以下の通りとなります。これだけを見るとセカンドプライスオークションが優れているため、こちらを採用したほうが良い感想を抱きますね。
- 耐戦略性はセカンドプライスオークションのみ
- 期待収入はファースト、セカンドともに同じ
実際の世界での適用例
これまでの結果を元に考えると、セカンドプライスオークションの方が有利な条件を保有しているように思えます。では実際の世界ではどうなのでしょうか。最も大きい広告プロダクトの一つであるGoogle AdXは2019年に以下のような発表をしています。
Simplifying programmatic: first price auctions for Google Ad Manager
https://www.blog.google/products/admanager/simplifying-programmatic-first-price-auctions-google-ad-manager/
端的にいうとオークション形式をセカンドプライスオークションからファーストプライスオークションに変更するといったものです。理由はいくつかあるのでしょうが、ここで示されているのはセカンドプライスで勝った後に、ウォーターフォールでファーストプライスで再度戦う場合など入札参加者はいくらで入札すべきか非常に複雑であり、これをシンプルにするため全てをファーストプライスオークションに切り替えるといった内容であると理解しています。
理論的に優れているセカンドプライスオークションですが、いくつか欠点もあり、そのため広く普及しているとは言いづらい状況です。
欠点1: 分かりづらいオークション形式
セカンドプライスオークションの最大の欠点はこちらです。例えば一般利用者が参加するオークションでセカンドプライスオークションを採用した場合、全員が理解できるのか?といった疑問があります。また評価値をそのまま入札すれば最善手となるのでしょうが、本当に入札者全員が財に対する真の評価値を算出することができるのでしょうか?皆さんもインターネットオークションに参加した際に、落札したい商品の真の評価額を算出しろと言われてもなかなか困るのではないかと思います。このようにセカンドプライスオークションは理論的には優れていても、実際に理解するのはなかなか難しいものがありますね
欠点2: 落札金額が信頼できるのか?
封印型セカンドプライスオークションを実施した場合に、落札金額は自分の入札金額ではない2番めの金額を支払うことになります。もしオークション主催者が不正を実施しようとした場合、封印型オークションは他社の入札金額がわからないため、この落札金額を不正に釣り上げることができます。このように主催者に信用がない場合、セカンドプライスオークション形式自体の信頼性が揺らぐため参加すること自体に二の足を踏み、オークションが滞る原因となりかねません
おわりに
以上オークション理論の基礎でございました。広告系エンジニアの方は常にファースト/セカンドプライスオークションを扱っていると思いますが、この理論的背景を知っておくのは有益かと思います。今回は超基礎編でしたが、機会があれば発展編を投稿できればなあと考えています。
参考文献
[1] 上田晃三(2010),“オークションの理論と実際:金融市場への応用”,金融研究,Vol. 29,No. 1,pp. 47-90
[2] 神山眞一(2015),“オークションにおける収入同値定理再考”,オイコノミカ 第 51 巻 第1号,2015 年,pp. 5-23
[3] マーケットデザイン入門:オークションとマッチングの経済学 坂井豊貴 ミネルヴァ書房
[4] オークション 理論とデザイン ポール・ミルグロム 東洋経済新報社
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。
一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD