【ノーベル賞×実務】pythonで簡単配属分け【ゲーム理論】

春だ！OJTだ！新人配属だ！

こちらは【競プロ×実務】pythonで簡単チーム分け【焼きなまし法】の（ある意味）続編となっています。

次世代システム研究室のT.Sです。前回は研修のチーム分けということでアルゴリズムをご紹介しましたが、そんな新卒の皆さんも入社から1ヶ月半を過ぎて、そろそろOJTが始まる季節ですね。ただ配属って簡単なようで実は難しい問題でして。。。いざ振り分けてみたものの不満が溜まったり、実はもっと適したスキルを持った人材がいたりと。深く考えてしまうとなかなか複雑な分野でありますが、今回はこれをゲーム理論で解決するアルゴリズムを紹介したいと思います。

ゲーム理論とは

ゲーム理論とは、市場に参加している各プレイヤーの意思決定や相互作用を数学モデルを用いて解析・研究する分野です。我々コンピュータ技術者には馴染みの深いジョン・フォン・ノイマンによって誕生した学問分野です。また「ビューティフル・マインド」という映画をご覧になった方も多いかと思いますが、この作品の主人公ジョン・ナッシュもゲーム理論研究者の一人であります。「ナッシュ均衡」という言葉はゲーム理論を知らない方でも聞いたことがあるという人は多いのではないでしょうか。ちなみにジョン・ナッシュはゲーム理論における貢献が認められ、1994年にノーベル経済学賞を受賞しています。

さてこのゲーム理論ですが、現代の経済学においては非常に重要な学問分野の一つになっています。ゲーム理論における分野として「メカニズムデザイン」や「マーケットデザイン」というものがあるのですが、これは理論が実際に活かされている例となります。

そういった実世界応用可能なゲーム理論分野の一つに「マッチング理論」というものがあります。これは人と組織などを効率的かつ安定的に組み合わせるもので、研修医の配属決定や患者と臓器提供者の組み合わせなどに使われています。2012年のノーベル経済学賞をシャプレーという研究者が受賞したのですが、これは安定配分理論と呼ばれるマッチング理論の一つに対する評価でありました。

今回はこの安定配分理論（DAアルゴリズム）を紹介し、ゲーム理論における効果的な人と組織のマッチングを知った上で、Python実装を併せて紹介したいと思います。

よくある考え方（ボストン方式)

さて人と組織を結びつける際によくある考え方はどんなものがあるでしょうか？

色々なケースが有るかとは思いますが、よくあるものとして「それぞれ配属希望を提出し、部署側がそれに従って所属者を決定する」といったものがあるかと思います。この手法をボストン方式と呼び、そのアルゴリズムは以下のようなものになります。

1. 各新人社員は、配属したい部署の希望順を提示する
2. 部署側はまず第一希望した新人社員のうち、許容可能な人員数内で、希望する上位から順に受け入れる
3. 第一希望で配属されなかった新人は、第2, 第3…と同様に割り当てる
4. 上記を繰り返し、全ての社員が配属されれば終わりとする

文字だけだと分かりにくいので図解で見てましょう。
前提として以下のような状況であると考えてください

• 新入社員は1,2,3,4,5の5人
• 配属部署はA,B,C,D,Eの5つ
• 研修での順位は1が最もよく、1,2,3,4,5の順位であった
• 各部署の定員は一人であり、どの部署も成績の優秀な新人社員順で配属を希望するものとする

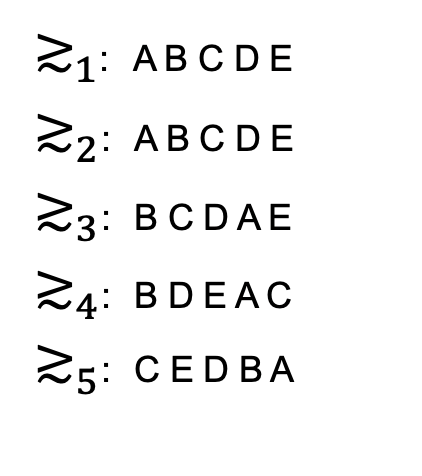
まず各新入社員は配属希望を提示します。
≿という記号が出てきますが、これは個人iの選好を表すものであります。 (≿ a b c)と記載されていた場合、aが最も希望が高く、cが一番低いものだと読み替えてください

この場合部署Eが人気がないですね… 相当ハードワークな部署であり、家に帰れないという噂でも立っているのでしょうか。その中でも新人5さんは研修のふがいなさを反省し、部署Eで鍛えてもらうことを考え一人だけ希望順位を高く持っているのかもしれません。

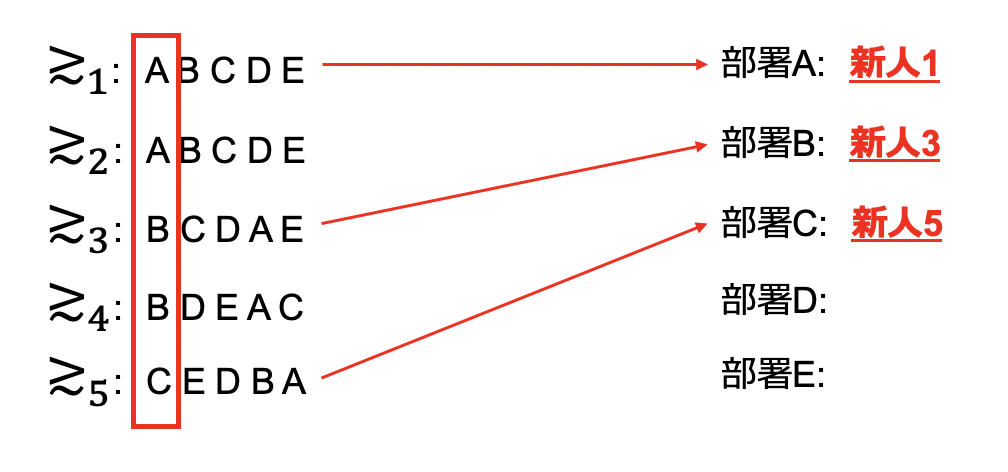
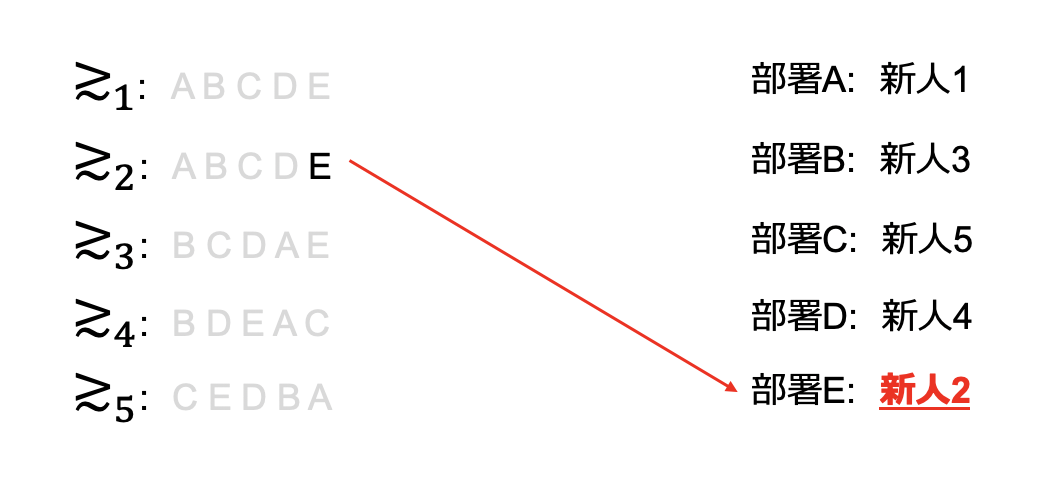
では第一希望の結果を見ていきましょう。

部署Aは新人1,2が希望しており、優秀な新人1が配属決定。部署Bは新人3,4が希望しており、優秀な新人3が配属決定。部署Cは新人5のみ希望していたので配属決定となります。新人5は気合をいれてEを志望したものの、第一希望に見事通ったようですね。

第2希望では新人2の希望はすでに埋まっているため、新人4の部署Dの配属のみ決定します

そして最後に新人2が部署Eに配属が決定し終了となります

問題点1: 不平等感（安定性）

さて改めて決定した配属を見てましょう。

この結果を見た新人2さんは「俺より成績が下位の人間が希望通りの部署に行っているのに、なんで俺は一番イヤだった部署なんだよ！」という不満を持つのではないでしょうか？これをきっかけに1年目にして退職の意志を固めてしまってもおかしくないかもしれません。

ではこれを以下の通り変更してみてはどうでしょう？新人5さんは第一希望から1ランク下がったものの、新人2さんは第5希望から第3希望に2ランク上昇し、差し引き1ランク分良い結果が得られているのが見えるかと思います。

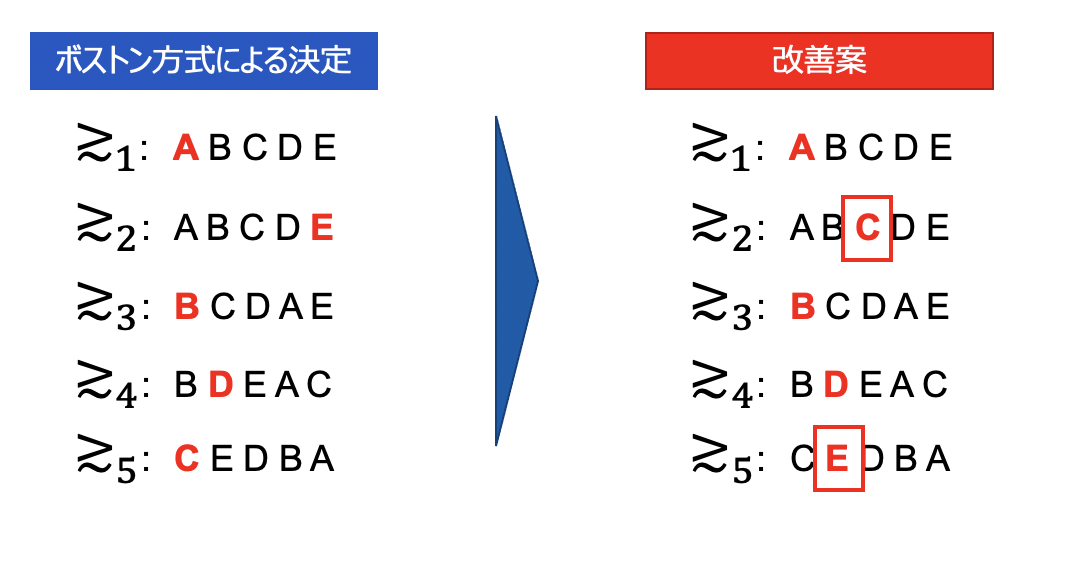
このようにある方式に基づいて決定されたマッチングについて、更に向上する余地があるとするならば、それはあまり良いアルゴリズムとは言えませんね。
ゲーム理論においてはこのような問題について、安定性や効率性と観点で評価し、こういった余地がないアルゴリズムを探すことが研究されていました。
安定性や効率性においては別途参考資料を御覧ください。

問題点2: 耐戦略性

もう一つ別の例を見てましょう。

配属希望を出す際に「所属Bは競争率が高いらしいぞ？」という噂が流れたとします。この場合新人2と新人3はどうしても部署Eに行きたくないがために、競争率の高い部署をBを回避して、部署Cの希望順位をあげてしまいました。
でもこういうことってよくありますよね。私も「あの研究室って倍率高いらしいから違うところにするか」といって希望を変えた大学時代を思い出します。

さてその結果以下のようになりました。

この場合、新人2は戦略的に希望順位を操作したことにより、本当の配属希望より良い結果が得られました。

ただこれもやはり良い傾向とは思えません。本来であれば自分の希望をそのまま伝えることが最も良い結果となれば一番いいはずです。こういったことが行き過ぎてしまうと「部署Aは競争率がやばいらしい。。。」といった噂に惑わされ、誰も志望しなかったということすら起きてしまいます。

マッチング理論ではこれを耐戦略性という観点で評価しています。戦略的な操作をしてしまうと必ず損をしてしまい、自分の希望をそのまま伝えることが最もよい利得を生み出す場合に、耐戦略性があると表現します。

上記2つを踏まえ、ボストン方式はあまり望ましくない方式であると言わざるを得ないでしょう。

改善策: DAアルゴリズム

1対1マッチング

さてボストン方式は安定的なマッチングは産まない方式であることはわかりましたが、どのようなアルゴリズムが良いのでしょうか？

ここで登場するのが先に延べたDAアルゴリズム（Gale-Shapleyアルゴリズム）になります。このアルゴリズムはボストン方式が抱えている安定性、効率性、耐戦略性の問題点を解消した上で、有限回数でマッチングできるという優れたアルゴリズムになっています。シャプレーはこのようなアルゴリズムや安定性などの評価基準を考えるなどの業績が評価され、マッチング理論に大きな発展をもたらしたとして2012年にノーベル賞を受賞しています。その際の受賞理由は「安定配分理論と市場設計の実践に関する功績」というものですが、この「安定配分理論」を実現するアルゴリズムこそがDAアルゴリズムになります。

このDAアルゴリズムは実務で色々使われているようです。日本においては早稲田大学高等学院の学生を、進学時に各学部に割り当てる際に使用されているとのことです（参考資料[1]より抜粋）。
また余談ですがGale-Shapleyアルゴリズムという名前からわかるとおり、この論文はDavid Galeという方との共著ありましたが、2012年時にはGale氏はなくなっていたためShapley氏のみ受賞となっております。

では早速先程の配属希望をDAアルゴリズムに適用してみましょう
DAアルゴリズムでは一人ずつ処理を逐次的に実行していきます。というわけでまず新人1の第一希望である部署Aに配属します。ただここからがボストン方式と違うのですが、ここでは正式配属ではなく、仮決定となります。

次に新人2の第一希望参照しますが、ここでは優先度の高い新人1がすでに仮決定しているため何も起こりません

これを全員の第一希望まで実施すると以下の通りとなります。

この次は新人1の順番ですが、既に仮決定されているためSkipします。そのため次は新人2の第2希望となります。

ここからがボストン方式と大きく異なってきます。新人2は既に新人3が仮決定されている部署Bを志望します。ここで部署Bは新人3より新人2の方が選好順位が高いため、新人3の仮決定を棄却し新人2を仮決定に変更します。新人2の研修で頑張りがようやく認められてよかったですね

次の順番は仮決定を棄却されてしまった新人3です。ここで同じように新人5が仮決定されている部署Cを希望し、この仮決定を奪い取ります。

これを繰り替えし、全ての新人が仮決定された段階で確定させます。結果は以下のとおりとなりますがボストン方式と比較すると、はるかに納得の行くものになっていることがわかるかと思います

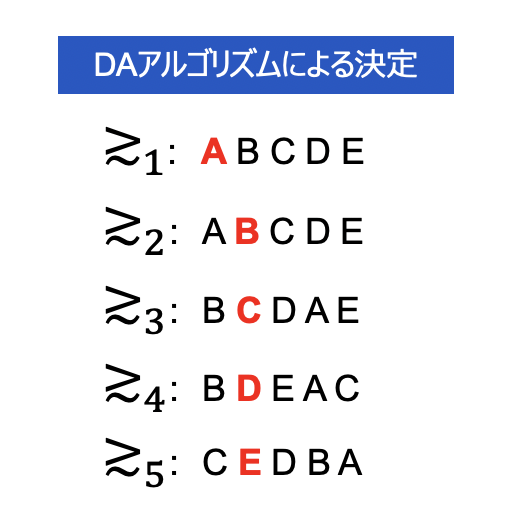
上記はかなり簡単の例のため、「そりゃそうだろう」と感じる方も多いかと思います。
しかしこれを大人数、かつ各組織で異なる選好を持った場合でも、同じように安定性、効率性、耐戦略性を持ったマッチング結果が有限回数で得られるというところがこのアルゴリズムの優れた点になります。

1対多マッチング

これまでは配属が1人で、しかも部署の選好が全て同じという簡単な事例でありましたが、これはかなり実務とは異なりますね。
そこで最後にもう少し現実に近い形にしたいと思います。

概要は以下の通りとします。大きく異なる点は配属部署が少なくなった上でそれぞれ選好を持ち、且つ定員数が複数人となっているところです。前回は1対1でのマッチングでしたが、今回は1対多のマッチングとなっている点が違っていますね。

• 新入社員は1,2,3,4,5,6,7,8の8人
• 配属部署はA,B,Cの3つ
• 新入社員と配属部署はそれぞれ異なる選好を持っている
• 配属部署は定員を持ちそれぞれ2,2,4とする

これを選好を表す式にすると以下の通りとなります。組織側にも選好を持っているのがこれまでと大きく異なります。実世界では部署によって必要なスキルも異なりますし、実世界により近いケースになったのではないでしょうか。

さて1対多マッチングの場合、DAアルゴリズムはどのような処理になるのでしょうか？仮決定するという基本コンセプトは同じであるのですが、キャパシティの概念が入ったため以下のように変更になっています。ちなみに「断る」という表現がありますが、これを便宜上の表現であります。「一回決まったのに断られるのって嫌だなあ」と思う方もいらっしゃるかもしれませんが、実際は最終決定のみ応募者には通知されますのであしからず。

1. 各新入社員はまず第一希望に応募する
2. 各部署は応募者のうち、キャパシティが許容するまで上位X人まで仮決定し、それ以外の人員を断る
3. 前回断られた新入社員は次の希望部署に応募する
4. 各部署は、これまでは仮決定した人員と新たに応募した人員をあわせ、上位X人まで仮決定し、それ以外の人員を断る
5. 3,4を繰り返し、新たな応募がなくなって時点で処理を終了し、最終決定とする

ではこのアルゴリズムに従い配属していきましょう。まず第一希望を元に配属します。その結果部署Aと部署Bは定員を超過してしまったため、選好上位である2名を仮決定として、それ以外を断ります。

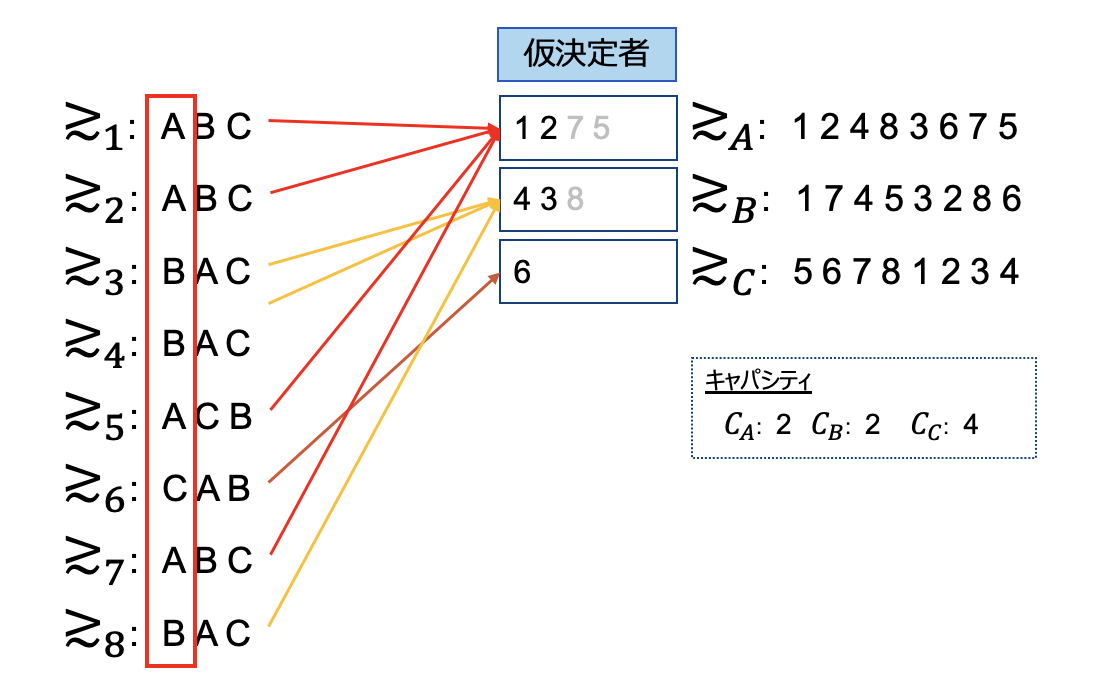
次に断られた新人5,7,8について第二希望を元に配属します。部署Aについては既に仮決定された新人1,2の方が優先順位が高いため、新たな応募を断ります。しかし部署Bについては新たに応募された新人7の優先順位が高いため、仮決定していた3を断ることになります。

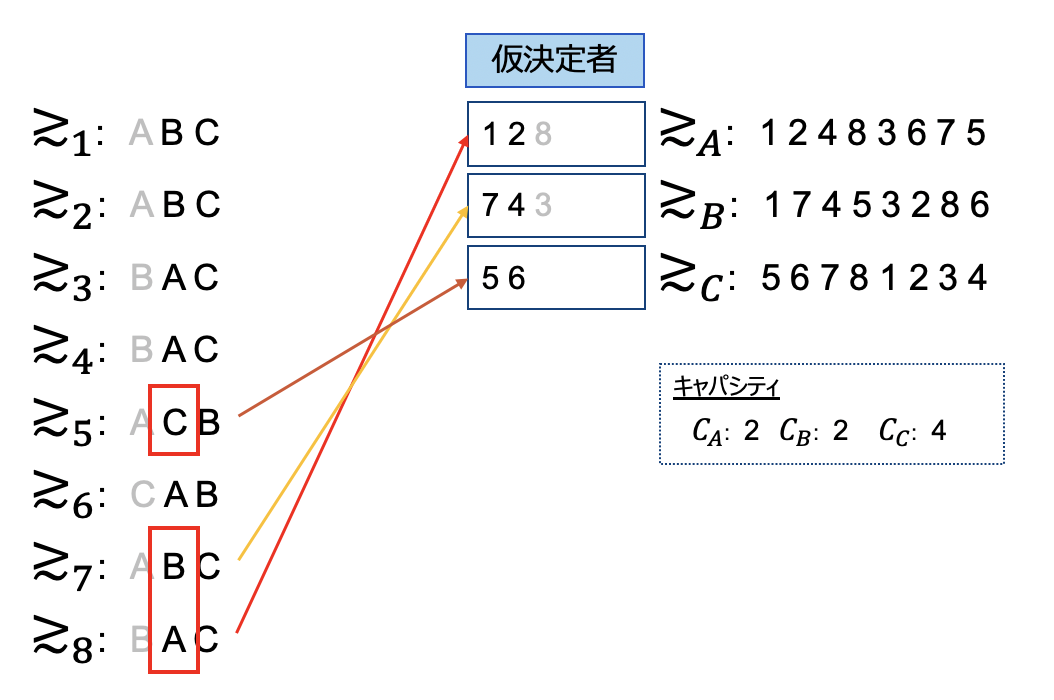
前ステップで断られた新人3,8について再度配属します。ここで注意したいのが新人3は第二希望、新人8は第3希望を応募する点にあります。ステップnだからといって、第n希望を適用するのではなく、あくまで未応募の中で最も順位が高いものに応募するという点を理解いただければと思います。

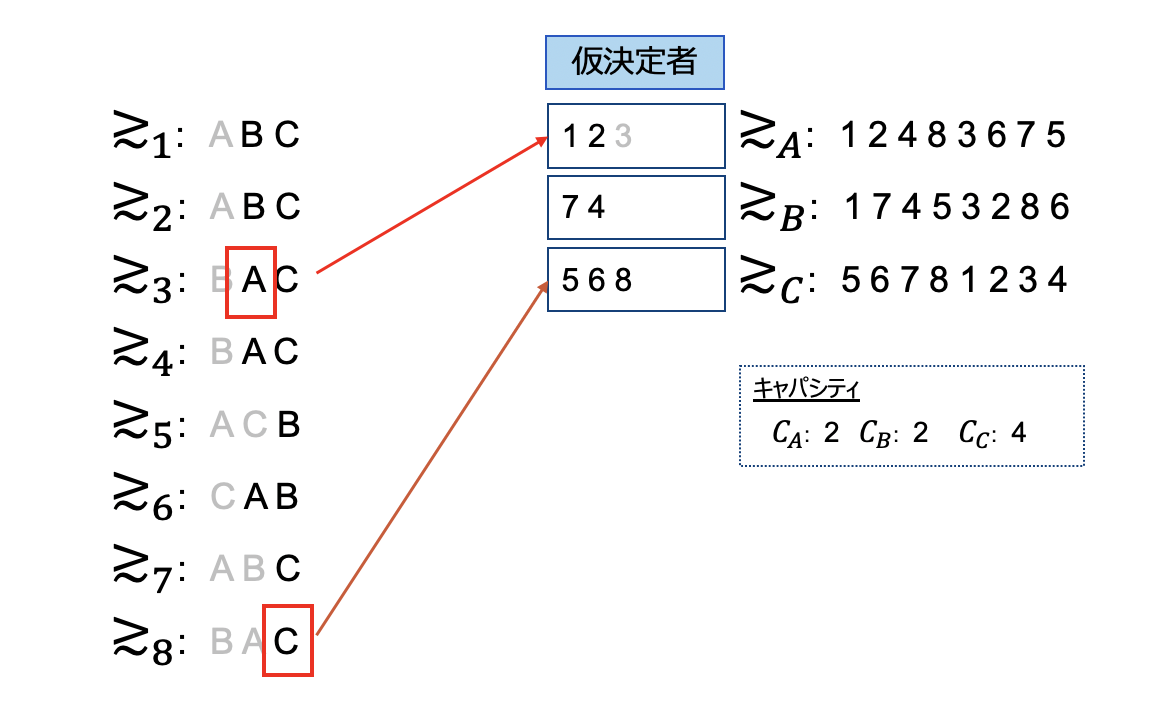
またも断られた新人3君は、最後第3希望に応募して処理終了となります。ちなみに今回は利用しませんでしたが選好は拒否を表す「0（正しくは0に斜線）」というものもあります。もし新人3の選好が（B A 0 C）で会った場合には、無所属として終了することになります。

1対多マッチングのPython実装

さてさてここまでDAアルゴリズムの内容をご紹介してきました。非常に簡単なものではあるのですが、それながら安定性、効率性、耐戦略性を兼ね備えた素晴らしいアルゴリズムであることに間違いはないかと思います。

というわけでここからは上記で紹介した1対多マッチングをPythonで実装していきたいと思います。

まず応募する新人さんのクラスを定義しましょう。
選好を持ち、STEPごとに応募する部署を特定するという2機能があればよいかと思われますので、このような実装にしてみました。

class BrandNew:

    def __init__(self, preference:list):
        self.preference = preference

    def pop_preference(self):
        if len(self.preference) == 0: return None

        return self.preference.pop(0)

次に部署側になります。STEPごとに応募を受付け、仮決定者を決める必要があるためこのような実装になっています。
各部署ごとに選好のソート順が異なるため、functools.cmp_to_keyを利用して簡単に実現しているところがちょっと工夫したところでしょうか？（大した話ではないですが）

from functools import cmp_to_key

class Department:

    def __init__(self, preference: list, capacity:int):
        self.preference: list = preference
        self.capacity: int = capacity
        self.__this_step_applicants: list = [] # 今回ステップの応募者
        self.__keep_members: list = [] # 現在の仮決定者

    def _compare_bn(self, arg1, arg2):
        l_index = self.preference.index(arg1)
        r_index = self.preference.index(arg2)

        return l_index - r_index

    @property
    def keep_members(self):
        return self.__keep_members   

    @property
    def this_step_applicant(self):
        return self.__this_step_applicants

    @this_step_applicant.setter
    def this_step_applicant(self, value):
        # 新しい応募者を設定
        self.__this_step_applicant = value
        # 現在の仮決定者と応募者をあわせて、仮決定者を再選する
        self.__keep_members = sorted(self.__keep_members + self.__this_step_applicant, key=cmp_to_key(self._compare_bn))[:self.capacity]

最後にこの2つのClassを使って、実際に配属していきます。
全て配属しきるまでLoopで処理していくだけの形にはなります。まあ有限回数で解けることが証明できているとのことなのでこれでもよいのかなと思います。
余談ですがwhile冒頭でpython3.8から導入された代入式を利用していますが、非常に便利ですね。代入した結果を返してくれるというだけでロジックをシンプルにすることが出来ました。

brand_news = {
    1: BrandNew(['A', 'B', 'C']),
    2: BrandNew(['A', 'B', 'C']),
    3: BrandNew(['B', 'A', 'C']),
    4: BrandNew(['B', 'A', 'C']),
    5: BrandNew(['A', 'C', 'B']),
    6: BrandNew(['C', 'A', 'B']),
    7: BrandNew(['A', 'B', 'C']),
    8: BrandNew(['B', 'A', 'C']),
}

departments = {
    'A': Department([1, 2, 4, 8, 3, 6, 7, 5], 2),
    'B': Department([1, 7, 4, 5, 3, 2, 8, 6], 2),
    'C': Department([5, 6, 7, 8, 1, 2, 3, 4], 4),
}

def not_keeped_applicatns(brand_news, departments):

    ## 新人全員をリストアップ
    all_applicants = set(brand_news.keys())

    ## 仮決定している人間をリストアップ
    all_keeps = [x.keep_members for x in departments.values()]
    all_keeps = set(chain.from_iterable(all_keeps))

    ## 差分を取り、今回処理対象者を決定
    return all_applicants - all_keeps

# 全て配属されるまで実行
while len(xs := not_keeped_applicatns(brand_news, departments)) > 0:
    # 仮決定されてない応募者を処理対象者とする
    for x in xs:
        target_dpts = brand_news[x].pop_preference()
        departments[target_dpts].this_step_applicant = [x]

print(departments['A'].keep_members)
print(departments['B'].keep_members)
print(departments['C'].keep_members)

結果は以下の通りと手計算と同じ結果が得られていますね

[1, 2]
[7, 4]
[5, 6, 8, 3]

[追記]最低人数制限がある場合

（質問があったため追記です）
これまでDAアルゴリズムを紹介するとともに、配属に利用できるアルゴリズムを紹介してきました。ただ実際よくある配属要件として「各部署に最低X名、最高でY名まで」といった制限が加わる場合があります。この場合従来のDAアルゴリズムでは対応できなかったのですが、これを拡張した「Extended-Seat DA」というアルゴリズムで解決できるため追記として紹介したいと思います。

まず要件を以下の通り変更してみます。配属部署の定員数を「各部署に最低X名、最高でY名まで」という形式に変更いたしました。

• 新入社員は1,2,3,4,5,6,7,8の8人
• 配属部署はA,B,Cの3つ
• 新入社員と配属部署はそれぞれ異なる選好を持っている
• 配属部署Aは最低1名、最大3名までの定員とする
• 配属部署Bは最低1名、最大2名までの定員とする
• 配属部署Cは最低3名、最大5名までの定員とする

この場合新しいアルゴリズムでは、定員をStandardとExtendedの2つに分けて考えます。
Standardは部署毎に設定され、それぞれの最低人数が定員数となります。しかしExtendedは部署横断で設定され、定員が「配属者数 – standardの合計」までとなります。つまり最低人数以上の人数分だけCapがかかってくるイメージになります。

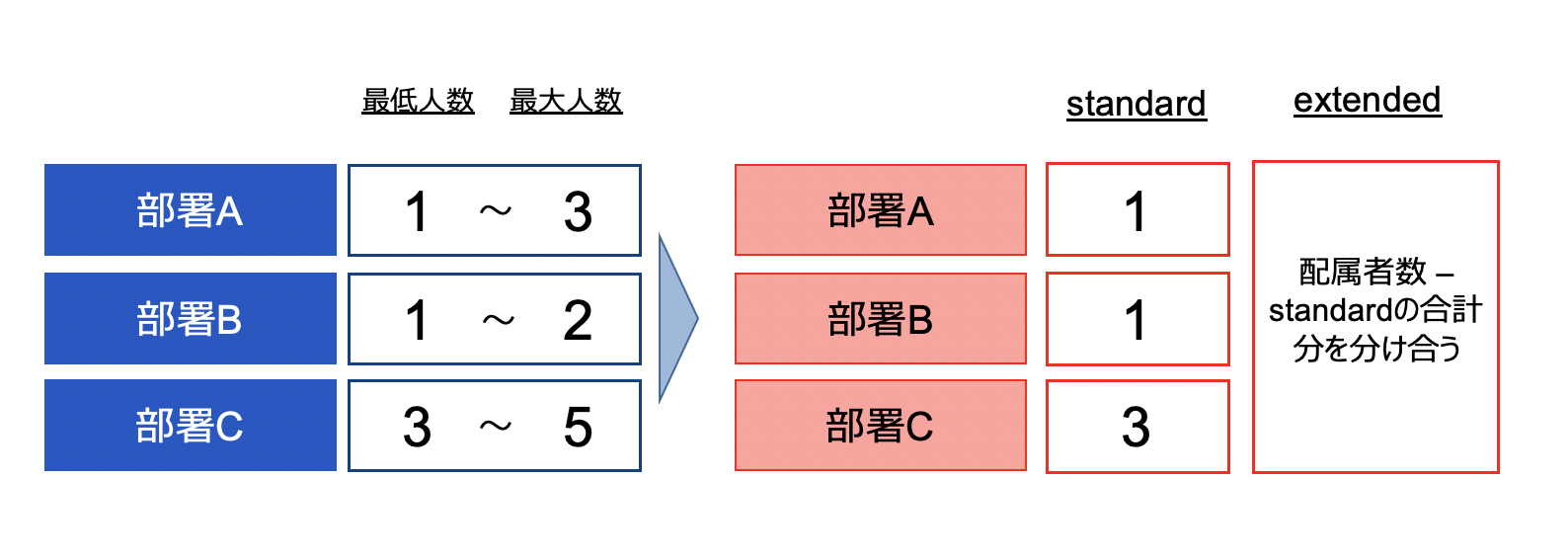
この考え方を実現するために選好を表す式も変更されます。これまでは部署A,B,Cの3つでしたが、それぞれの部署をStandardとextendedの2つに分けることになります。この際選好は同一のものを利用しますが、定員数は変更されstandard=最低人数、extended=(最大人数-最低人数)をというものを設定します。extendedという概念に伴い、それに当たる部署が増加する形ですね。

部署がextended分だけ増えてしまったので、これに対応するべく新卒側の選好も変更します。変更方法は簡単で、従来の選好それぞれの直後にextendedを挿入する形になります。

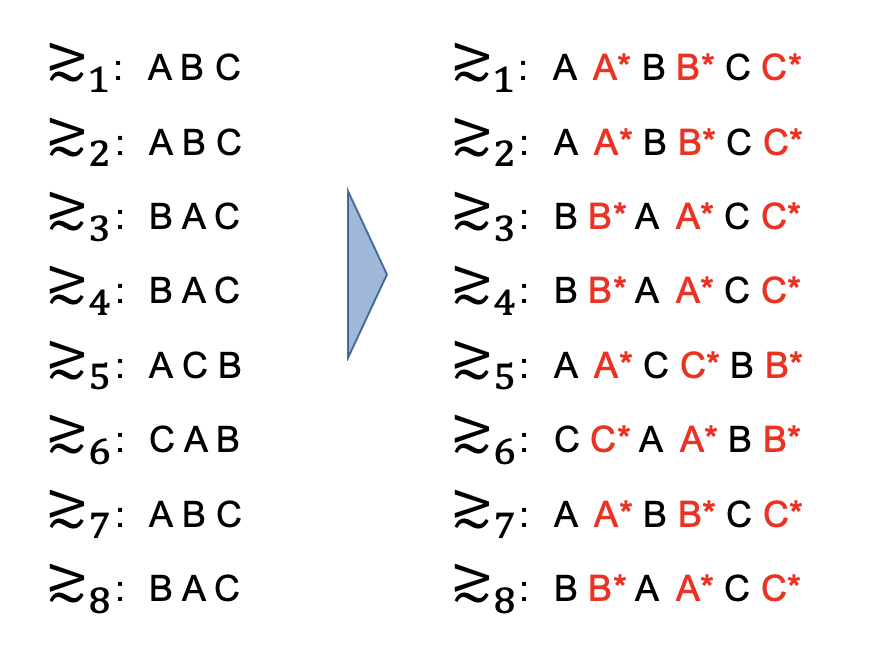
さて準備はできたので配属していきましょう。ここからの基本コンセプトはDAアルゴリズムと同じにものになります。ただ一点注意点として、extendedに配属された数が、Cap（配属者数 – standardの合計）を超えないようにしなければいけません。ここでのCapは新人の数[8]から部署の最低人数の合計[1+1+3=5]を引いた[3]になります。

一番最初の配属はこれまでどおりですね。特に変わった点は有りません。

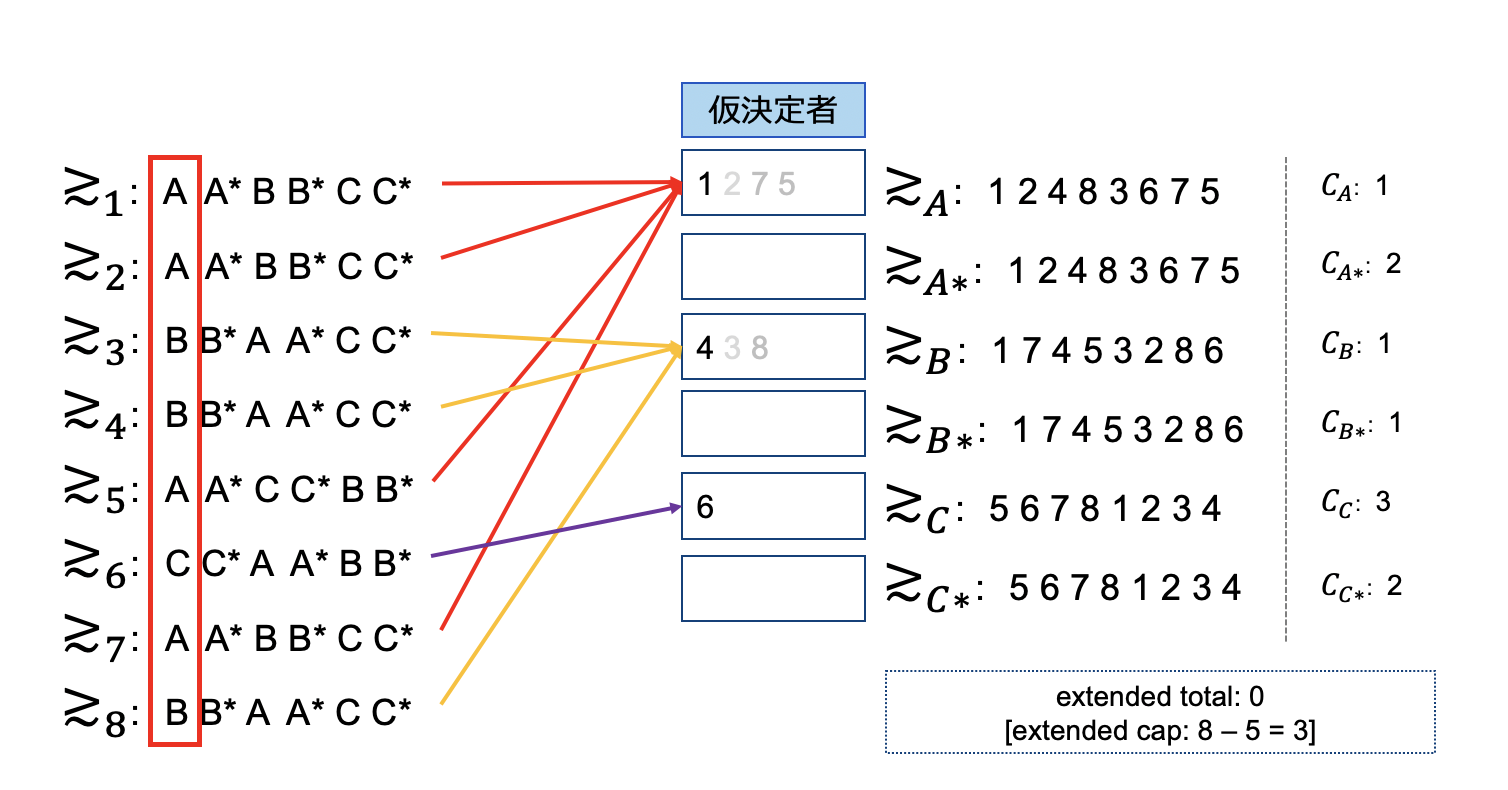
第2段階目は、増分されたextended分が対象となります。ここでの配属の結果、extendedに配属された人数はCapと同じ値である3人のため特に制限はせず従来どおり終了します。ちなみに元論文には、この処理を「One by One（ひとつずつ）」実施しろとの記載があるため、本来であればまとめてやってはいけないのですがここは簡単のため一括処理しています。ご容赦ください。

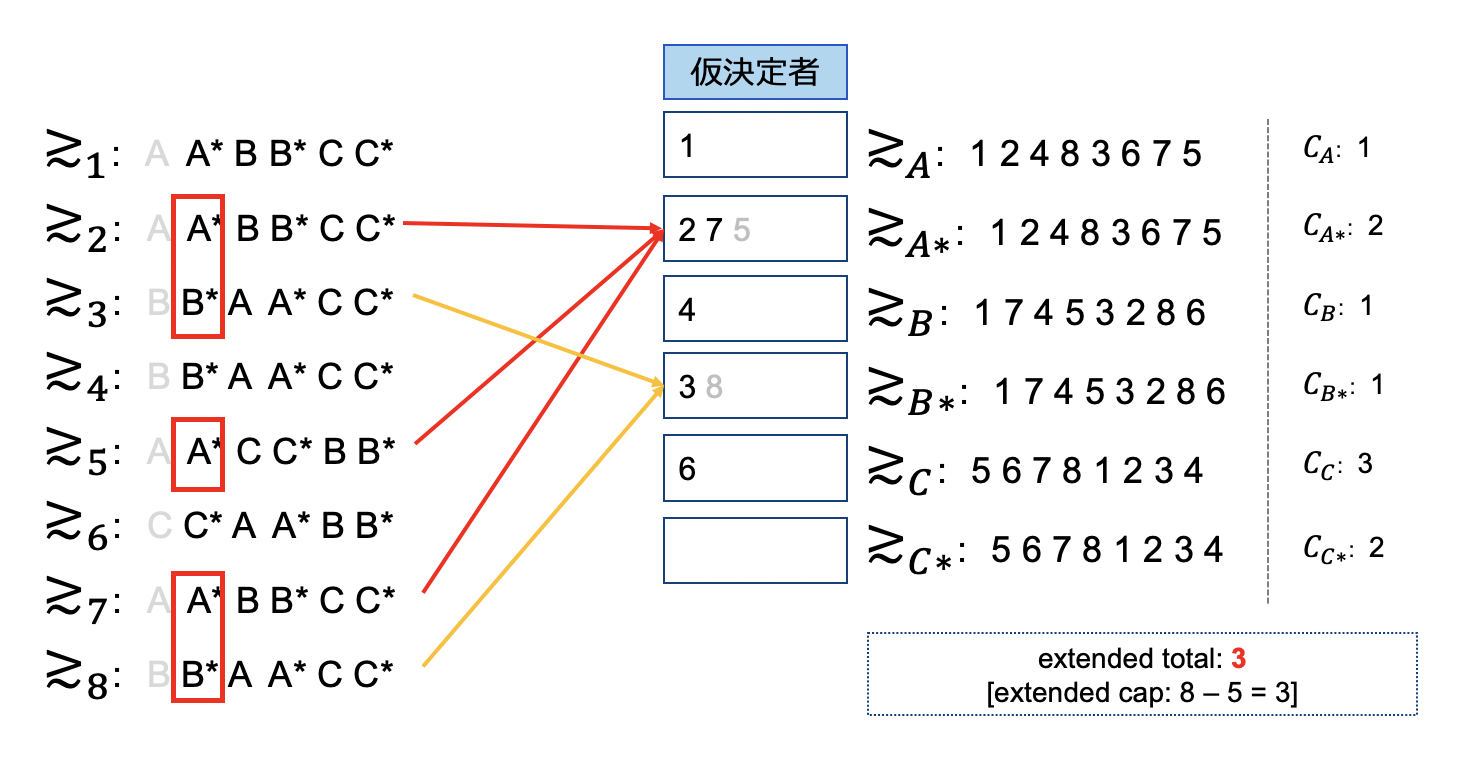
次STEPも従来DAアルゴリズムどおりです。

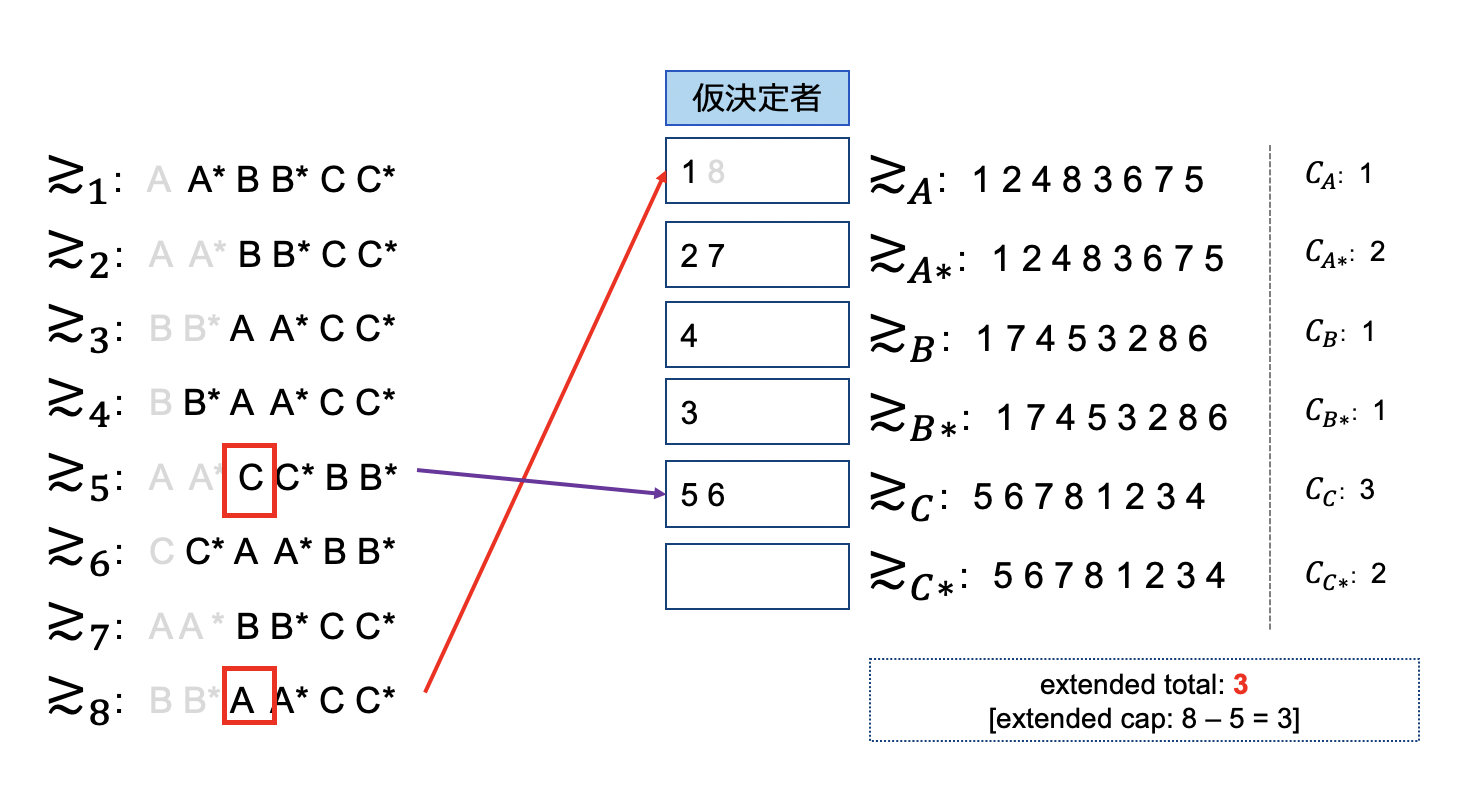
さて残るは新人8さんだけになりました。ここでは部署Aのextendedに配属が希望されています。従来アルゴリズム通りですと、新人7を追いやることができるのですが、ここではCapを既に超えているため割当せず処理をスキップします。ここが従来と異なる点になります。

extendedの上限かかり、割り当てられなかった新人8を最後に部署Cに割り当て終了となります。

これにてマッチング終了ととなります。DAアルゴリズムを少し拡張するだけで、安定的なマッチングが得られました。
ただ一点このアルゴリズムでは新人側からは安定的なマッチングを実現しているものの、部署側はそうではないということを留意下さい。下限制約が加わると、なかなか悩ましい問題が発生しますね…

おわりに

以上いかがでしたでしょうか？
ノーベル賞に関連する理論としてはかなりとっつきやすいものなかったでしょうか？ゲーム理論という分野がなにをやっているか、そして現実世界でどうつかわれているか、その一端を垣間見るには良い題材ではなかったかなと思います。今回のマッチング理論に限らず、オークションなど我々の周りではゲーム理論が応用されている箇所は数多くあります。非常に面白い分野であるので、是非興味がある方は勉強してみると面白いかと思います

参考文献

[1] マーケットデザイン入門:オークションとマッチングの経済学　坂井豊貴　ミネルヴァ書房
[2] ゼミナール ゲーム理論入門　渡辺隆裕　日本経済新聞出版
[3] NABENAVI.NET
[4] Fragiadakis, D., Iwasaki, A., Troyan, P., Ueda, A., and Yildirim, M.: Strategyproof Matching with Minimum Quotas(2015)

次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。
一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。