【競プロ×実務】pythonで簡単チーム分け【焼きなまし法】

春だ！研修だ！チーム分けだ！

次世代システム研究室のY.Cです。皆さん、チーム分けしてますか？ 研修やzoomのブレークアウトセッション等、チーム分けが必要な場面はそれなりにあると思います。ランダムで割り振るのは簡単ですが、なるべく所属が分散するようにとか、前回と重複しないようにとか、条件を付けていくと途端に難しくなります。このような場面で便利なのが焼きなまし法です。今回はpythonのパッケージを利用して、お手軽に焼きなまし法の威力を体験してみたいと思います。

TL;DR

• 焼きなまし法は、少しずつ改善を繰り返すアプローチ方法で、規模の大きな問題にも対応できてすごい
• simannealパッケージで、簡単に焼きなまし法を実装できる
• pythonは遅い

焼きなまし法とは

焼きなまし法は最適化問題を解くための手法で、マラソン系の競技プログラミング(複雑な問題に対して、時間をかけ少しでもよい結果を出すのが目的)でよく使われます。例えば、いくつかの都市を一巡するための最短経路を求める巡回セールスマン問題では、厳密解を求めようとすると都市をまわる順番を全て洗い出すこととなり、指数関数的な時間がかかってしまいます。このような時は、近似解を求めるアプローチをとります。”現在の都市のまわり方の過程を少しだけ変えて経路が短くなったら採用する”をひたすらに繰り返す、などの手法です。

 

一見、この改善をひたすら繰り返せば良い解に近付くように見えますが、都市のまわり方に対する最短経路の分布は単調であるとは限らず、むしろ上図のようにデコボコしているかもしれません。そうした場合、ひたすら改善を繰り返す=谷へ向かう方向へ移動すると、スタート地点によっては局所的な解にハマってしまうことがあります。焼きなまし法では、一定の確率で改悪=山へ向かう方向への移動を許容することで、局所解にハマることを防ぎます。この確率を試行の序盤ほど高く、終盤ほど低くすることで、最終的には大局的な解に至ることを目指します。

simannealパッケージの紹介

前述の焼きなまし法をお手軽に実装できるpythonのパッケージでsimannealというものがあります。これを使うと必要最小限の部分を実装するだけで済みます。githubにあるサンプルコード(simanneal/examples/salesman.py)を例にとり、簡単に使用方法をみてみます。

class TravellingSalesmanProblem(Annealer):

    """Test annealer with a travelling salesman problem.
    """

    # pass extra data (the distance matrix) into the constructor
    def __init__(self, state, distance_matrix):
        self.distance_matrix = distance_matrix
        super(TravellingSalesmanProblem, self).__init__(state)  # important!

まず、Annealerクラスを継承したクラスを作成します。探索のスタート地点となる状態は全て一つのオブジェクトに詰め込み、コンストラクタにstateとして与えます。コメントにimportant!とある通りここが重要で、探索過程ではこのstateをコピーして、移動するなら新しいstateを採用、移動しないならコピーしておいたstateを採用、ということを繰り返します。逆に探索の過程で不変である要素は、distance_matrixのように自由に追加できます。

    def energy(self):
        """Calculates the length of the route."""
        e = 0
        for i in range(len(self.state)):
            e += self.distance_matrix[self.state[i-1]][self.state[i]]
        return e

コストを計算するメソッドを定義します。前述の例で言うところの”現在の都市のまわり方における経路長を求める”部分です。注意点として、このパッケージではコストを最小化する方向への移動が改善と見なされます。そのため何かを最大化したい場合は、返り値にマイナスをかけてやるとよいです。

 

    def move(self):
        """Swaps two cities in the route."""
        # no efficiency gain, just proof of concept
        # demonstrates returning the delta energy (optional)
        initial_energy = self.energy()

        a = random.randint(0, len(self.state) - 1)
        b = random.randint(0, len(self.state) - 1)
        self.state[a], self.state[b] = self.state[b], self.state[a]

        return self.energy() - initial_energy

状態を移動させるメソッドも定義します。前述の例で挙げた “都市をまわる過程を少しだけ変える” の部分です。ここでは何もリターンしなくてよいですが、移動によるコストの差分をリターンすることもできます。前述の例で言うと、”都市のまわり方を変えることで経路長がどれだけ増えたか/減ったか”です。差分を返すことで、移動の度にコストを再計算しなくて済むため高速化に繋がります。(この例はself.energy()を呼び出してしまっているので高速化はしないですが、このように差分を返すこともできるということを示しています)

    tsp = TravellingSalesmanProblem(init_state, distance_matrix)
    tsp.set_schedule(tsp.auto(minutes=0.2))
    # since our state is just a list, slice is the fastest way to copy
    tsp.copy_strategy = "slice"
    state, e = tsp.anneal()

あとはインスタンスを生成して、状態移動時のコピー方法を指定して、実行するだけです。ここでは状態がリストなので”slice”を指定すると高速です。困ったら”deepcopy”にすることで、状態をまるっとコピーできます。set_scheduleによって大まかに時間を指定してイテレーションの回数を調整していますが、なくても動きます。個人的には tsp.steps = 10**6 のようにして直接回数を指定する方が扱いやすいです。

はい、これだけです。ちょー簡単ですね！では早速チーム分けをしてみたいと思います。

チーム分け

問題：凄腕つよつよエンジニアのあたなは、人事の研修担当の方から、以下の50人を指定された条件に従ってチーム分けするよう依頼された。可能な限り良いチームの分け方を出力せよ。

条件1: 所属部署、性別がなるべく重複しないよう、8チームに分ける。
条件2: 所属部署がなるべく重複しないよう8チームに分けることを、5回繰り返す。このとき、可能な限り毎回異なるメンバー構成にする。

※以下データは、もちろん完全にダミーです！実際のケースをイメージして部署1,部署2に人数を偏らせています。

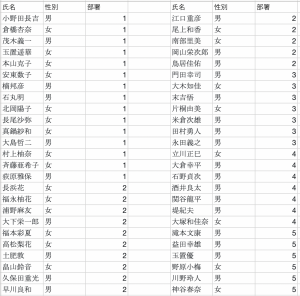
条件1:属性によるチーム分け

問題の整理

所属部署、性別といったメンバーの属性が重複しないようにするにはどうすればよいでしょうか？先ほどの巡回セールスマン問題を振り返ると以下の最適化を行なっていました。

• 現在の都市をまわる順番に対して、都市間の距離を合計し、全体の経路長を計算
  -> 経路長を最小化

これに照らし合わせると、今回は次のように整理できます。

• 現在の各チームのメンバー構成に対して、チーム内で重複する属性の数を合計し、全体の重複度を計算
  -> 重複度を最小化

ここまで言い換えると実装できそうですね！

実装

2次元リストmembers に、[‘氏名’, ‘性別’, ‘所属部署’]の順にメンバーの情報が入っているものとします。

# メンバーの人数
num_members = len(members)
# チームの数
num_team = 8
# メンバーの所属チーム; はじめは順番に割り振っておく
member_team = [ i % num_team for i in range(num_members)]
# 各チームの各性別の人数
gender_count_by_team = [defaultdict(int) for _ in range(num_team)]
# 各チームの各部署別の人数
department_count_by_team = [defaultdict(int) for _ in range(num_team)]

for i in range(num_members):
    gender_count_by_team[member_team[i]][members[i][1]] += 1
    department_count_by_team[member_team[i]][members[i][2]] += 1
# 初期状態
init_state = [member_team, gender_count_by_team, department_count_by_team]

こんな感じで初期状態を定義しておきます。重複度を簡単に計算できるよう、各メンバーの所属チームを表すリスト、(チーム毎の各性別の人数の辞書)のリスト、 (チーム毎の各部署の人数の辞書)のリスト、の3つを用意しています。

 

 

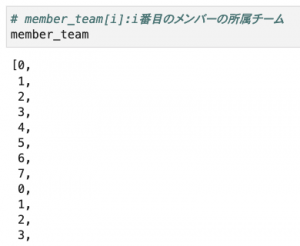
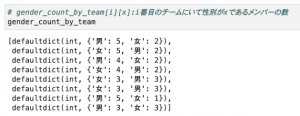
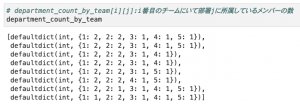
初期状態の中身はこのようになっています。

# チームtにおける重複度
def calc_team_cost(t, gender_count_by_team, department_count_by_team):
    # 性別の重複度：　男女の人数差の二乗
    g = abs(gender_count_by_team[t]['男'] - 
    gender_count_by_team[t]['女']) ** 2
    
    # 部署の重複度: 重複した人数の二乗
    d = 0
    for v in department_count_by_team[t].values():
        d += max(0,v-1)**2

    return g + d

チーム内での重複度を計算する関数を定義しておきます。同じ属性が何度も重複するのを避けるため、二乗することで重み付けしてみました。

from random import choice
class GroupingProblem(Annealer):
    def __init__(self, init_state):
        super(GroupingProblem, self).__init__(init_state)  # important!

    def move(self):
        
        # ランダムにa,bの２人選ぶ
        a = choice(range(num_members))
        b = choice(range(num_members))
        # 同一人物だった場合、何もせず終了(重複度の差分は0)
        if a == b:
            return 0
        # a,bそれぞれのチーム
        a_team = self.state[0][a]
        b_team = self.state[0][b]
        # ２人が同一チームだった場合、何もせず終了(重複度の差分は0)
        if a_team == b_team:
            return 0
        
        # 各チームのメンバー交換前の重複度
        cost_a_before = calc_team_cost(a_team, self.state[1], self.state[2])
        cost_b_before = calc_team_cost(b_team, self.state[1], self.state[2])

        # aのチームのaの性別の人数,aの部署の人数をデクリメント
        self.state[1][a_team][members[a][1]] -= 1
        self.state[2][a_team][members[a][2]] -= 1
        # bのチームのbの性別の人数,bの部署の人数をデクリメント
        self.state[1][b_team][members[b][1]] -= 1
        self.state[2][b_team][members[b][2]] -= 1
        
        # a,bの所属チームを交換
        self.state[0][a], self.state[0][b] = self.state[0][b], self.state[0][a]

        # aの新しいチームのaの性別の人数,aの部署の人数をインクリメント
        self.state[1][b_team][members[a][1]] += 1
        self.state[2][b_team][members[a][2]] += 1
        # bの新しいチームのbの性別の人数、bの部署の人数をインクリメント
        self.state[1][a_team][members[b][1]] += 1
        self.state[2][a_team][members[b][2]] += 1
        
        # 各チームのメンバー交換後の重複度
        cost_a_after = calc_team_cost(a_team, self.state[1], self.state[2])
        cost_b_after = calc_team_cost(b_team, self.state[1], self.state[2])
        
        # メンバー交換による重複度の差分を返す
        return cost_a_after - cost_a_before + cost_b_after - cost_b_before
        
        
    
    # 目的関数
    def energy(self):
        # 各チームの重複度の和を返す
        return sum(calc_team_cost(i, self.state[1], self.state[2]) for i in range(num_team))

Annealerクラスを継承させたクラスを作成し、移動のメソッドとコストを計算するメソッドを実装します。移動メソッドは複雑に見えるかもしれませんが、やっていることとしてはランダムに2人選んでチームを入れ替えているだけです。それに伴って性別の人数・部署の人数を減らしたり増やしたりしています。

prob = GroupingProblem(init_state)
prob.steps = 10**6
prob.copy_strategy = "deepcopy"
state, e = prob.anneal()

では実行してみます！

結果

焼きなましして得られた各チームの男女の人数と部署毎の人数です。例えば4番目のチームは、男女がそれぞれ3人で、部署1〜5までの人数が、それぞれ1,2,1,1,1となっています。概ねいい感じに分散できていますね！

条件2:過去同じチームになった回数によるチーム分け

問題の整理

続いて、可能な限り異なるメンバー構成で複数回チーム分けを行いたいと思います。例に倣って、まず何を最適化したいのか日本語で考えてみます。先ほどは、

• 現在の各チームのメンバー構成に対して、チーム内で重複する属性の数を合計し、全体の重複度を計算
  -> 重複度を最小化

でした。今回は1度同じチームになった人同士が2回以上同じチームになることを避けたいわけです。するとこのように言えそうです。

• 現在の各チームのメンバー構成に対して、チーム内のメンバーのペアの過去同じチームになった回数を合計し、全体の重複度を計算
  -> 重複度を最小化

やや複雑度が上がりましたが、実装はできそうですね。

実装

メンバーの数^2の二次元リストを用いて、メンバー同士で過去同じチームになったことのある回数を記録します。

# メンバーの人数
num_members = len(members)
# チームの数
num_team = 8
# メンバーの所属チーム; はじめは順番に割り振っておく
member_team = [ i % num_team for i in range(num_members)]
# 各チームのメンバー
team_to_member = [[] for _ in range(num_team)]
# 各チームの各部署別の人数
department_count_by_team = [defaultdict(int) for _ in range(num_team)]

for i in range(num_members):
    team_to_member[member_team[i]].append(i)
    department_count_by_team[member_team[i]][members[i][2]] += 1
# 初期状態
init_state = [member_team, team_to_member, department_count_by_team]

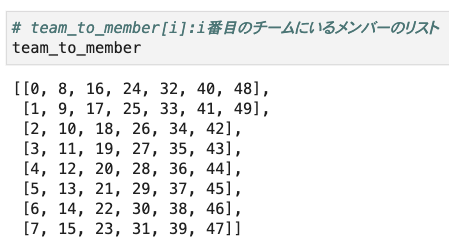
今度は、先ほどの状態からチーム毎の男女の人数を取り除き、代わりにチーム毎のメンバーを表すリストを追加します。

 

 

# チームtにおける重複度
def calc_team_cost(t, team_to_members, department_count_by_team, num_same_team):
    g = 0
    
    # チームtに属するメンバー
    team = team_to_members[t]
    
    # チーム構成の重複度：過去にチームメンバー同士が同じチームになった回数 ** 2
    for i in range(len(team)):
        m1 = team[i]
        for j in range(i+1,len(team)):
            m2 = team[j]
            g += num_same_team[m1][m2] ** 2
    
    # 部署の重複度: 重複した人数の二乗
    d = 0
    for v in department_count_by_team[t].values():
        d += max(0,v-1)**2

    return g + d

from random import choice
class GroupingProblem(Annealer):
    def __init__(self, init_state, num_same_team):
        super(GroupingProblem, self).__init__(init_state)  # important!
        self.num_same_team = num_same_team

    def move(self):
        
        # ランダムにa,bの２人選ぶ
        a = choice(range(num_members))
        b = choice(range(num_members))
        # 同一人物だった場合、何もせず終了(重複度の差分は0)
        if a == b:
            return 0
        # a,bそれぞれのチーム
        a_team = self.state[0][a]
        b_team = self.state[0][b]
        # ２人が同一チームだった場合、何もせず終了(重複度の差分は0)
        if a_team == b_team:
            return 0
        
        # 各チームのメンバー交換前の重複度
        cost_a_before = calc_team_cost(a_team, self.state[1], self.state[2], self.num_same_team)
        cost_b_before = calc_team_cost(b_team, self.state[1], self.state[2], self.num_same_team)

        # aのチームのaの部署の人数をデクリメント
        self.state[2][a_team][members[a][2]] -= 1
        # bのチームのbの部署の人数をデクリメント
        self.state[2][b_team][members[b][2]] -= 1
        
        # aのチームのリストからaを除く(効率悪いが横着)
        self.state[1][a_team].remove(a)
        # bのチームのリストからbを除く(効率悪いが横着)
        self.state[1][b_team].remove(b)
        
        # a,bの所属チームを交換
        self.state[0][a], self.state[0][b] = self.state[0][b], self.state[0][a]

        # aの新しいチームのaの部署の人数をインクリメント
        self.state[2][b_team][members[a][2]] += 1
        # bの新しいチームのbの部署の人数をインクリメント
        self.state[2][a_team][members[b][2]] += 1
        
        # aの新しいチームのリストにaを追加
        self.state[1][b_team].append(a)
        # bの新しいチームのリストにbを追加
        self.state[1][a_team].append(b)
        
        # 各チームのメンバー交換後の重複度
        cost_a_after = calc_team_cost(a_team, self.state[1], self.state[2], self.num_same_team)
        cost_b_after = calc_team_cost(b_team, self.state[1], self.state[2], self.num_same_team)
        
        # メンバー交換による重複度の差分を返す
        return cost_a_after - cost_a_before + cost_b_after - cost_b_before
        
        
    
    # 目的関数
    def energy(self):
        # 各チームの重複度の和を返す
        return sum(calc_team_cost(i, self.state[1], self.state[2], self.num_same_team) for i in range(num_team))

重複度を計算する関数やAnnealerを継承させた問題クラスでも、同じチーム内のメンバー同士で過去同じチームになったことのある回数を考慮するように変更します。これで準備は整いました。

 

from copy import deepcopy
# メンバー同士が同じチームに属した回数を記録
def record_num_same_team(num_same_team, team_to_member):

    num_same_team_next = deepcopy(num_same_team)

    for m in team_to_member:
        for i in range(len(m)):
            m1 = m[i]
            for j in range(i+1, len(m)):
                m2 = m[j]
                num_same_team_next[m1][m2] += 1
                num_same_team_next[m2][m1] += 1
    return num_same_team_next
    

for i in range(5):
    prob = GroupingProblem(init_state, num_same_team)
    prob.steps = 10**5
    prob.copy_strategy = "deepcopy"
    state, e = prob.anneal()
    num_same_team = record_num_same_team(num_same_team, prob.state[1])

 

焼きなましを実行 -> num_same_teamに同じチームになった回数を記録 という工程を5回繰り返して、メンバー同士のペアで2回以上同じチームになった回数を計測してみます。

結果

最終的に、2回同じチームになったことのあるペアの数は67となりました。ペアの数は全部で 50*49/2 = 1225で、1チーム6~7人のチーム分けを5回繰り返してこの数字ですから、一定の成果が得られたとは言えそうです。

プチ考察

本記事での気付きです。

コピーが遅い

今回私の環境では、10**6回のイテレーションでも2分半かかっています。かなり遅いです。原因の一つは、deepcopyを用いて状態のコピーを行なっていることです。deepcopyは便利ですが状態を全てコピーするため遅いです。状態移動時のコスト計算と同様に差分だけコピーできるようにすることで、より高速化が期待できます。詳細はパッケージのソースコードsimanneal/anneal.pyを参照ください。とてもコメントが丁寧で、読むだけで勉強になります。

pythonが遅い

気付いてしまったのですが、そもそもpythonは遅いです。データが100人規模になるだけで、10**6回のイテレーションに15分近くかかってしまいまいました。たぶんコピーが遅いとかいう次元じゃないです。もっと巨大なデータに対して、複雑な試行を何回も繰り返す際は他の高速な言語を選択肢に入れるべきです。ただ、本記事で紹介したパッケージの圧倒的手軽さは正義です。悩ましい。

 

おわりに

焼きなましの便利さ、少しでもお伝えできたでしょうか？記事ではざっくり実装して実行してみただけですが、実際にチーム分けを行なった際はあまり所属や性別が分散してくれなかったため、メンバーの偏りを見ながらわざと少しだけ重複を許容するといった調整を行いました。試行錯誤しながら改善を繰り返すのは、やはり面白いです。

最近はAtCoder Heuristic Contest の新設等、競技プログラミング界隈でもマラソン系コンテストが大きな盛り上がりをみせており、マラソンを始めるなら最高のタイミングであると言えます。私もこのビッグウェーブに乗って精進し、細かいチューニングについてバリバリ語れるようになりたいです。

次世代システム研究室では、 Web アプリケーション開発を行うアーキテクトを募集しています。募集職種一覧 からご応募をお待ちしています。