2024.02.06
AlphaGeometry: 数学オリンピック金メダリスト級(幾何学限定)の「ファスト&スロー」なハイブリッド生成AI
TL;DR
- GoogleのDeepMindが先日(2024/01/17)に「AlphaGeometry」という数学の幾何学問題を解くAIを公開しました。
- ノーベル経済学賞受賞者のDaniel Kahneman の提唱する「ファスト&スロー」の考え方に基づいて直感的な早い思考「言語モデル」と論理的で遅い思考「記号推論エンジン」を組み合わせたハイブリッド・モデルです。問題解決のプロセスは、記号推論エンジンでの証明試みに失敗した場合、言語モデルで補助線を導入し、再び記号推論エンジンで証明を試みるという手順をを繰り返します。
- 言語モデルの学習には、約10億個のランダムに生成した前提と、そこから導出された定理から重複などを除いた1億個の証明文を利用します。これらのデータで事前学習し、更に補助線の必要な問題でファインチューニングしました。
- 国際数学オリンピックの幾何学問題のうち30問中25問をAlphaGeometryは解くことができました。これは金メダル受賞者(上位1/12以内)に匹敵する成績です。更に、AlphaGeometryは、2004年の問題に対して、より一般化された定理の導出にも成功しています。
- AlphaGeometryのコードはGitHubで公開されています。学習済みのモデルも利用可能で、簡単にAlphaGeometryの性能を試すことができます。
- ただし、AlphaGeometryはあくまで幾何学の問題に特化したモデルであるため、実際の数学オリンピックで金メダルを受賞するには他の数学分野も解けるように改良する必要があり、幾何学以外の問題への拡張は今後の課題となります。
はじめに
こんにちは、グループ研究開発本部・AI研究室のT.I.です。2024年に入っても、日々、新たなAI技術が続々と発表されています。2024/01/17に、GoogleのDeepMindはAlphaGeometryというAIモデルを発表しました。これは数学の幾何学(geometry)の問題を解くことに特化したAIです。その能力は数学オリンピックの金メダリスト級に匹敵すると話題になっています。AlphaGeometryの成績は以下の通りです。
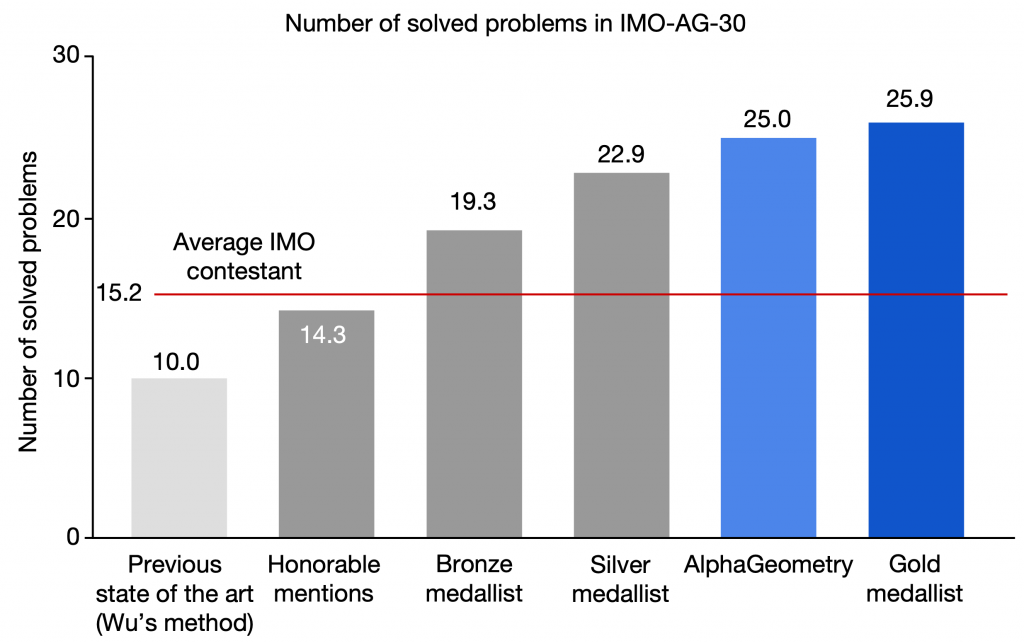
AlphaGeometryの国際数学オリンピックの幾何学問題の成績(図はAlphaGeometryの論文より)
これは2000年から2022年までの、国際数学オリンピックの幾何学問題計30問(IMO-AG-30)のうち正解した問題の数です。AlphaGeometryは金メダリストに匹敵する25/30の問題に回答し、従来のState-of-the-Artの10問を圧倒しております。なお、メダル受賞者の点数ですが、実際の競技では各問ごとに0-7の点数で評価されるものを0-1の範囲に正規化して集計しています。
確かに興味深いAIの成果ですが、さて、ここで一息ついて、何をしたのか整理しておきます。
まず、国際数学オリンピック(International Mathematical Olympiad (IMO))とは、高校生を対象とした数学の競技会です。昨年の2023年は、日本の千葉で開催され112カ国の参加国から618名の参加者があり、日本のチームは6位に入賞しました(国際数学オリンピック(IMO2023)結果より)。出題範囲は高校2年程度(注:日本のカリキュラムと若干異なります)の数学に限定されてはいるものの、非常に高い難易度の問題が出題されます。数学オリンピック財団の公式サイトとWikipediaによると概要は以下の通りです。
- 各国6名以下の選手+団長・副団長で構成されたチームが参加
- テストは2日間で、1日4時間半で、3問づつ計6問を解く
- 各問題は7点満点で採点
- 合計6問で満点は42点
- 持ち込める道具は定規とコンパス類のみで計算機などは使用不可
- 一定以上の点数の参加者(上位半数以上)から1:2:3程度の割合で金、銀、銅のメダルを授与
- メダル受賞者でなくとも少なくとも1つの問題で満点(7点)を取れば、優秀賞を授与
- 出題範囲
- 整数問題
- 幾何学
- 組み合わせ数学
- 代数学
ですので、金メダリストとなるには少なくとも上位1/12以内の成績を収める必要があります。また、微積分や複素数、確率統計、行列、三角関数などの数学分野は出題範囲に含まれていません。
各大会の問題は公式サイトで公開されています。例えば、2022年の問題2は以下の通りです。
\(\mathbf{R}^+\) を正の実数全体からなる集合とする. 関数 \(f: \mathbf{R}^+ \rightarrow \mathbf{R}^+\) であって, 任意の \(x \in \mathbf{R}^+\)に対して, \(xf(y) + yf(x) \leq 2\) なる \(y \in \mathbf{R}^+\)がちょうど 1 つ存在するようなものをすべて求めよ.
このような問題が全部で6題あります。
で、AlphaGeometryはこのうちの幾何学の問題を解くことに特化したAIモデルです。国際数学オリンピックでは、年によりますが多くて2つ程度の幾何学の問題が出題されます。幾何学って何?と思われるかもしれませんが、以下のような図形に関する問題です。点同士の関係性や角度などの前提(premise)を与えて、それから図形の各種性質を利用して証明するべき結論(conclusion)を導き出す問題です。
2022年の問題4
\(BC=DE\)なる凸五角形\(ABCDE\)の内部に点\(T\)があり,\(TB=TD\),\(TC=TE\), \(\angle ABT = \angle TEA\) をみたしている. 直線\(AB\)は直線\(CD\), \(CT\)とそれぞれ点\(P\) , \(Q\) で交わっており, \(P\), \(B\), \(A\), \(Q\) はこの順に並んでいる. また, 直線 \(AE\) は直線\(CD\), \(DT\)とそれぞれ点\(R\), \(S\) で交わっており, \(R\), \(E\), \(A\), \(S\)はこの順に並んでいる. このとき, \(P\), \(S\), \(Q\), \(R\) は同一円周上にあることを示せ.
ここで注意ですが、AlphaGeometryは言語モデルを構成要素に持つ、まあ所謂、“生成AI”と呼ぶことができるAIです。ただし、言語モデルのみで幾何学の問題を解答するのではありません。実質的に数学の計算を処理するのは、記号推論エンジンというルールベースのAIです。
DeepMindの公式ブログでは、IMOの金メダリストでフィールズ賞の受賞者のNgô Bảo Châuのコメントが紹介されています。
AIの研究者たちが、まずIMOの幾何学問題に挑戦しているのは、今となっては完全に納得がいく。なぜなら、この種の問題の解を見つけるのは、各ステップ毎の合理的な選択がかなり少ないという点で、チェスに似ているからだ。しかし、それでも彼らがこの問題を成功させたことに驚きを覚える。感動的な成果だ。(DeepLによる翻訳を修正)
このコメントにあるように幾何学の問題への解答は一定のルールに従って進めることができます。そのための記号推論エンジンと通常では人の直感(?)が必要な証明プロセス(=補助線の追加)を言語モデルが行い互いに補完することで、AlphaGeometryは国際数学オリンピック級の幾何学問題を解くことができるのです。
AlphaGeometryとは
DeepMindの公式ブログで、AlphaGeometryの概念として、ノーベル経済学賞受賞者のDaniel Kahneman の提唱する「ファスト&スロー」の考え方が紹介されています。(訳註: DeepMindのBlogではKahnemanの出版物へのリンク込みで the idea of “thinking, fast and slow” となっており、著書の邦題は「ファスト&スロー」ですので、ここではそれを用いています。)これは、人の意思決定には一瞬で直感的に判断する「ファスト」の思考であるSystem 1と、時間をかけて論理的に判断する「スロー」の思考のSystem 2があるというものです。前者の「ファスト」の思考は、他人の表情から感情を読み取るなど無意識のうちにされる処理です。後者の「スロー」の思考は時間をかけて論理的な判断を行うもので、計算問題のような複雑で意識的な処理に用いられます。
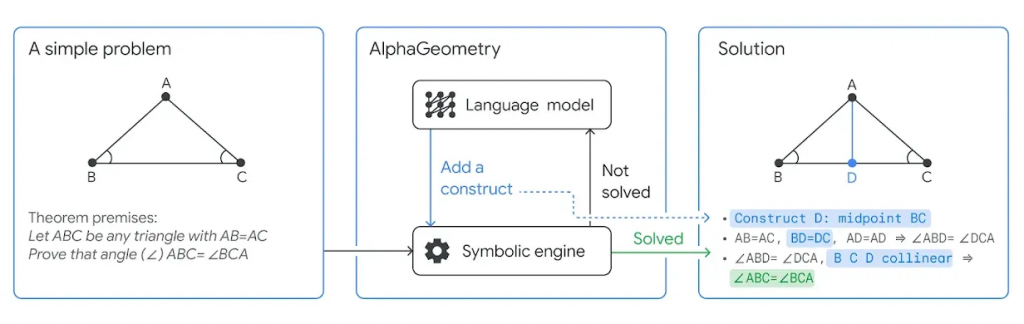
AlphaGeometryの概念図(DeepMindの公式ブログより引用)
AlphaGeometryは与えられた問題に対して、まずは「スロー」の思考である記号推論エンジン(Deductive Database(DD)+Algebraic Rules(AR))で回答を試みます。(訳註: 原著論文では、“symbolic deduction engine”と記載されています。無理に直訳するなら記号演繹エンジンかと思いますが、あまり見かけない表現ですので、Neuro-symbolic AI の分野でより一般的な表現である記号推論(symbolic reasoning)という表現を用いています。なお、Nature公式の注目記事の翻訳でも同様に記号推論エンジンとしています。)このステップで解が得られない場合、次に、「ファスト」とされる言語モデル(LM)を使って、補助線の追加を行います。そして、再び記号推論エンジンで問題が解けないかを試みることを繰り返して問題解決を行います。最終的に得られる証明は人が理解できる形式で出力されます。AlphaGeometryはこのような手法でIMOの幾何学問題を解決します。人の場合は、先に「ファスト」が働き、必要に応じて「スロー」を呼び起こして物事を処理するのですが、AlphaGeometryはこの順番は逆転しています。また計算処理としては明らかに重たいはずのLMの処理が「ファスト」として機能する点も興味深いですね。
このような記号推論と深層学習モデルのハイブリッドの構造は、AlphaGeometryが初めてではありません。第3次AIブームで登場した大量の教師データに基づいた深層学習モデルの次世代型AIとして提唱され研究が進められています。例えば、2021のIJCAIの招待公演では、Yoshua Bengioは、“System 2 Deep Learning: Higher-Level Cognition, Agency, Out-of-Distribution Generalization and Causality”というタイトルで、この「ファスト&スロー」の思考を組み合わせたハイブリッドなモデルについて講演しています。(https://ijcai-21.org/invited-talks/)
上記の例題は、\(\triangle ABC\)に対して、\(AB=AC\)という前提条件に対して、\(\angle ABC = \angle BCA\)を証明する問題です。AlphaGeometryでは、記号推論エンジンで証明できないかまず試みますが、これだけでは条件が不足しており証明できません。そこで、言語モデルが、新たに点\(D\)を\(BC\)の中間(\(BD = DC\))に追加します。再び記号推論エンジンで証明を試みます。
- \(\triangle ABD\)と \(\triangle ACD\)は、それぞれの辺の長さが等しいので合同 \(\triangle ABD \equiv \triangle ACD\)
- したがって、\(\angle ABD = \angle ACD\)
- そして、\(BCD\)、同一の線上にあるので、\(\angle ABD = \angle ABC\)、\(\angle ACD = \angle ABC\)
- 以上から\(\angle ABC = \angle BCA\)
AlphaGeometryでは、このような過程により問題を解決します。
AlphaGeometryの学習過程
では、AlphaGeometryの技術の詳細を紹介します。言語モデルを学習するには、良質で大量のデータセットが不可欠です。しかし、そのような数学の問題+証明のセットのデータなど、どこにあるでしょうか? ないなら作ればいいじゃない、というのがAlphaGeometryのアプローチです。
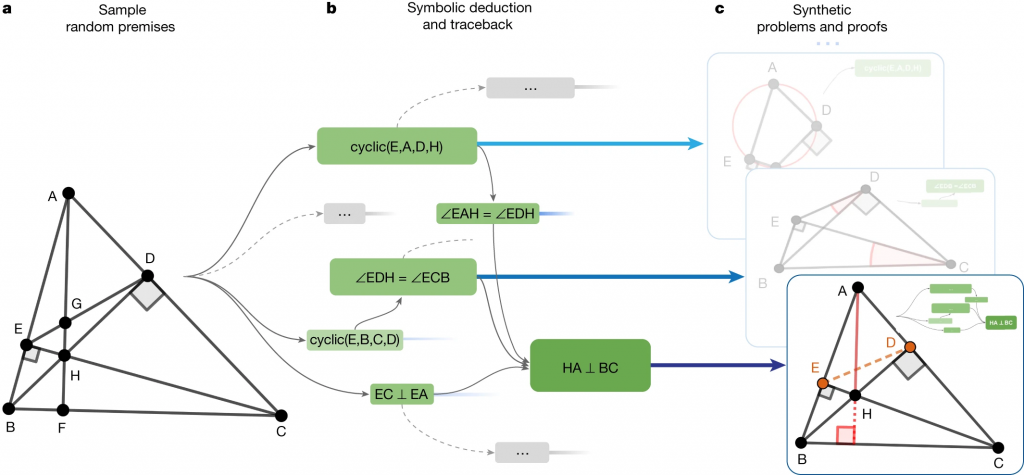
AlphaGeometryの学習データの作成の概念図(図はAlphaGeometryの論文より)
まず、ランダムな定理の前提を約10億個ほど生成します。それを記号推論エンジンに入力し、前提から様々な命題を導き出します。導出された命題は、有向非巡回グラフとして表現されます。そのサブグラフ\(G(N)\)を証明(proof)、\(P\)を前提(premises)、\(N\)を結論(conclusion)とすると、データセットは、(premises, conclusion, proof) = \((P, N, G(N))\)の組みで表現されます。
記号推論エンジンは具体的には、Deduction Database(DD)という幾何学の法則のルールのリストと代数計算の処理Algebraic Rules(AR)の組み合わせとなっています。ARも使うことで、DDだけでは導出できない命題も導出することができます。

記号推論エンジン(DD+AR)の動作の例(AlphaGeometryの論文より引用)
さて、後述しますが、実は記号推論エンジンのみでも数学オリンピックの問題を14/30を解くことができます。しかし、記号推論エンジンでは、補助線の作図が必要な幾何学の問題を解くことができません。これが従来のルールベースのモデルの限界です。
そこで、言語モデルで、生成したデータセット\((P, N, G(N))\)を学習します。結局は文字列ですので、LLMと同様にNext-token predictionとして、もっともらしい証明文を生成できるように訓練します。AlphaGeometryでは、1.51億のパラメーターサイズのTransformerを採用しております。LLMなのかというと、少々、微妙なサイズ感ではありますが、GPT-1(約1.17億)よりは大きいですね。
以下の図は、問題を解決するために必要なステップ数(横軸)と対応する問題数(縦軸)を表したヒストグラムです。縦軸がログスケールで表されており、ステップ数が増えるにつれて問題の数が急速にすくなることが分かります。ランダムに生成した問題ではありますが、既知の定理も含まれております。特に、証明に必要なステップ数が少ない問題への大きな偏りが見られ大部分を占めております。重複する問題を除いて、1億個の問題に絞りました。これらの訓練データには実際に数学オリンピックの問題は含まれていないことは確認されております。言語モデルの学習では、これらの1億個の生成したデータを事前学習に使用します。さらに、補助線が必要な問題を抽出して、これらに特化したファインチューニングを施します。補助線が必要な問題は全体の約9%の900万件で、残りの91%は純粋に推論のみで解ける問題です。
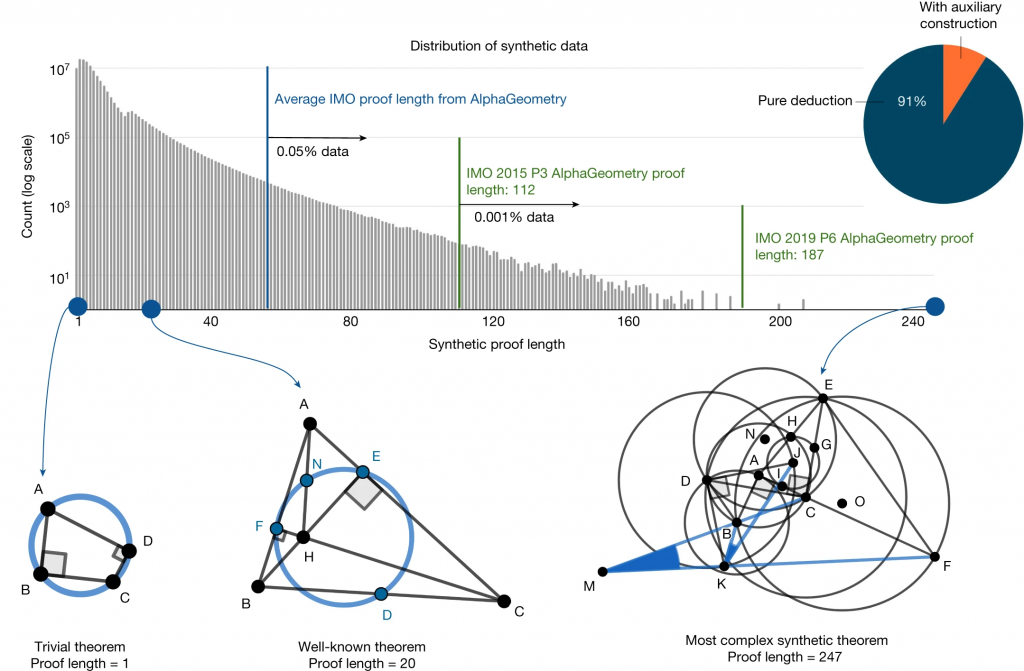
AlphaGeometryで合成した定理の件数と証明に必要なステップ数の分布(AlphaGeometryの論文より)
AlphaGeometryの性能
このようにして学習したAlphaGeometryで数学オリンピックの幾何学問題に挑戦します。2000年から2015年の問題から幾何学のみを抽出して、IMO-AG-30 datasetを作成しました。AlphaGeometryの生成する回答は、人が読める形式として出力されます。これを実際のUSA IMOチームのコーチに採点(0-7の点数)をしてもらいました。DeepMindのBlogでは、このコーチ(IMO Gold medalist Evan Chen)のコメントが紹介されています。
AlphaGeometryの出力が印象的なのは、検証可能でクリーンだからだ。証明に基づく競技問題に対する過去のAIによる回答は、ヒット・オア・ミス(出力が時々しか正しくなく、人によるチェックが必要)になることがあった。AlphaGeometryにはこのような弱点はない。その解は機械的に検証可能な構造を持っている。にもかかわらず、その出力は人が読むことができる。プログラムが幾何学の問題を解くというと、座標系を力業で総当たりすることを想像するかもしれない、何ページにもわたる退屈な代数計算だ。AlphaGeometryはそうではない。AlphaGeometryは、角度や相似三角形に関する幾何学のルールを生徒と同じように利用する。(DeepLによる翻訳を修正)
AlphaGeometryが問題を正確に回答した際には、満点の7点を獲得しました。数学オリンピックでは、幾何学の問題は年によって出題数が変動します。2000年と2015年の大会では、2つの幾何学の問題が出題されました。AlphaGeometryはこれらすべての問題に正解しました。これは該当の大会で合計14点を獲得することに相当し、その成績はメダル受賞者の水準を超えるそうです。なお、実際の数学オリンピックでは、3つの問題に対して4.5時間の制限時間がありますので、AlphaGeometryも4.5時間と1つ当たりに換算して1.5時間の制限時間で問題が解答可能か検証しています。最も難しい問題(2008/1a)に関しては、1.5時間制限で解くために最大でCPUを246並列する必要がありますが、大半の問題は、1 CPUでも1.5時間以内に解答可能です。
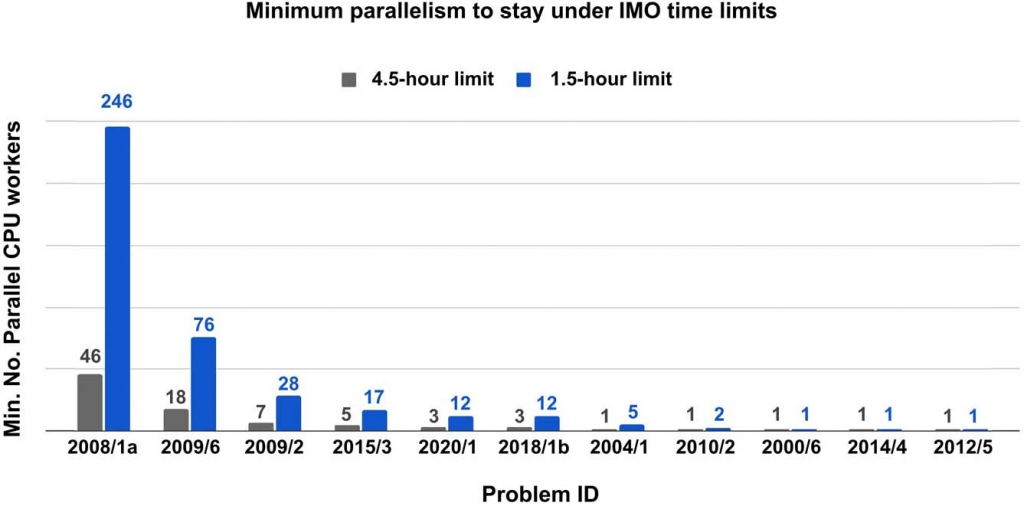
AlphaGeometryがIMO-30の問題を制限時間内に解くために必要なCPU(AlphaGeometryの論文より)
AlphaGeometryと他のアプローチの結果の比較は以下のテーブルです。幾何学の問題を解く方法としては、補助線を引いて角度や幾何学的性質を利用する他に、問題を代数学的な方程式に変換して解くことも可能です。Gröbner基底とWu’s methodというのは、そのように変換後の方程式を代数的に解く技術です。しかし、これらの手法で国際数学オリンピックの問題のような高度な問題を解く場合には、計算コストが非常に多くかかります。また、証明のプロセスを人が読める形式では出力できません。この検証では48時間の制限時間で問題が解けるかという点で、これらの手法を評価しています。
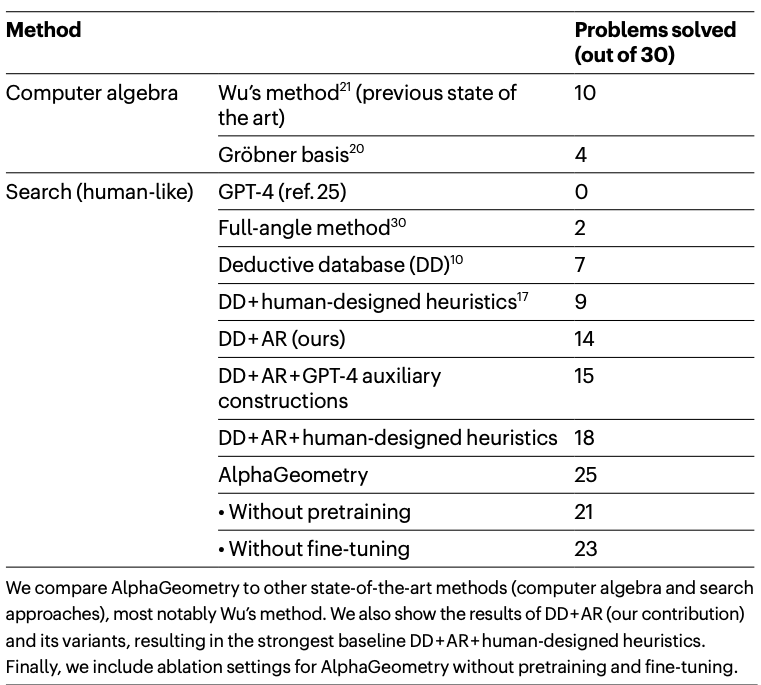
各種アプローチでIMO-30で解答できた問題数の比較(AlphaGeometryの論文より)
AlphaGeometryは30問中の25問の回答に成功し、これまでのState-of-the-Artの手法(Wu’s method)の10問を圧倒しています。また、人のように幾何学の問題を解くアプローチの中でも、AlphaGeometryは最も多くの問題を解答しています。GPT-4では全く回答できていませんが、DD+ARのみでも14問も回答できています。AlphaGeometryは、全データを用いた事前学習なしでは21問(注:訓練データの20%のデータで学習した場合)、ファインチューニングなしでは23問なので、大量のデータでの事前学習とファインチューニングの効果があることがわかります。なお、GPT-4の解答に関しては、IMOの問題と解答に関する情報を学習時に含まれている可能性がある点にも注意が必要です。
AlphaGeometryの成果で興味深い結果が以下のIMO2004の問題で証明にあります。 AlphaGeometryは特定の条件(点\(O\)の位置)を仮定せずに、この問題を解決しました。これは、点\(O\)がどのような位置にあっても結論が証明可能であること、そして、点\(P\)は\(BC\)の間にあるという制約も必要ないことを示しています。結果として、AlphaGeometryの証明はより一般的な定理を導き出すことに成功しました。
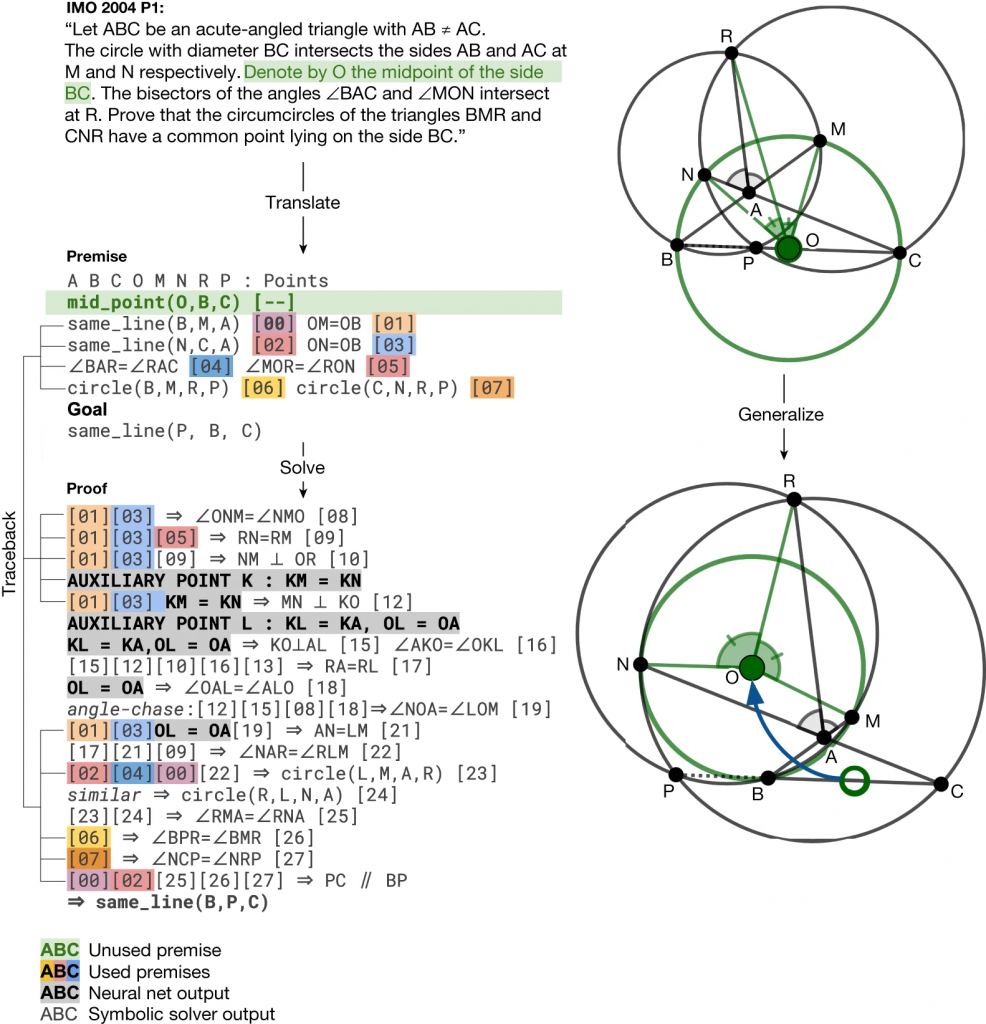
IMO 2004 P1 のAlphaGeometryによる証明(AlphaGeometryの論文より)
ちなみに、AlphaGeometryに与えるIMO-AG-30 datasetの文字列は以下のような文章となっております。各々の点やその関係性を定義し証明するべき命題を記述しています。
translated_imo_2004_p1 a b c = triangle a b c; o = midpoint o b c; m = on_circle m o b, on_line m a b; n = on_circle n o b, on_line n a c; r = angle_bisector r b a c, angle_bisector r m o n; o1 = circle o1 b m r; o2 = circle o2 c n r; p = on_circle p o1 r, on_circle p o2 r ? coll p b c
上記のAlphaGeometryの証明は、人が読み解ける形式で提示されていますが、そのプロセスは人の証明と比較して冗長で、洗練されていないとも評価されています。これは推論ルールの制限やより高度な数学技術の不足によるものと考えられます。これは、AlphaGeometryの技術が将来的に更に改善される可能性があることも示唆しています。
個々の問題の大会での平均点とAlphaGeometryの証明ステップの長さを比較した結果が以下の図です。
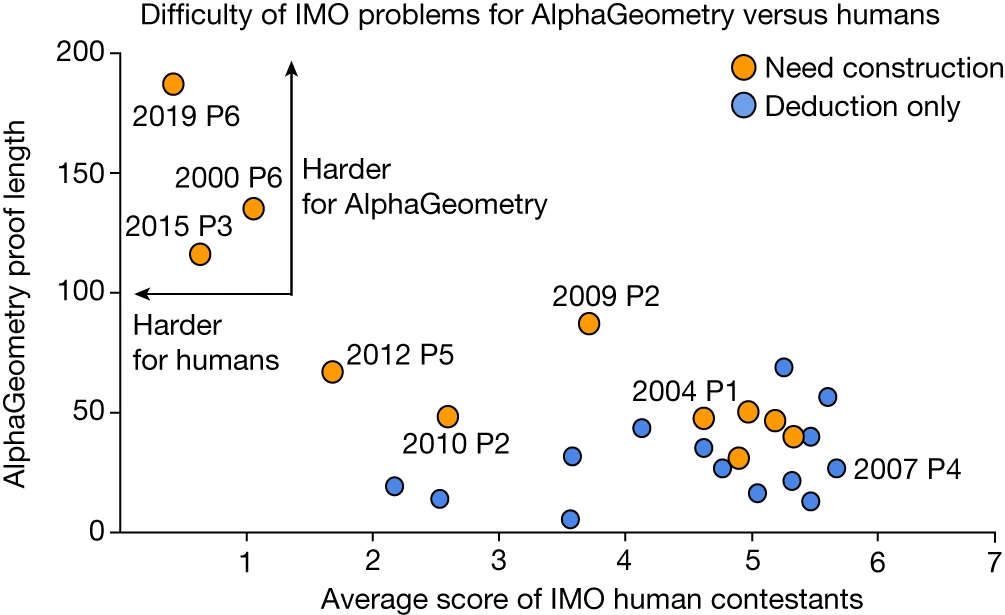
数学オリンピックの問題ごとの平均点とAlphaGeometryが証明に要したステップ数の分布(AlphaGeometryの論文より)
興味深いのは、左上に分布している問題で、人の平均点が低い難しい問題の場合、AlphaGeometryも証明までに長いステップを要している点です。ただし、単純に参加者の点数とAlphaGeometryのステップ数には相関は見られなかったそうです(\(p = -0.06\))。
AlphaGeometryを動かしてみる
では、このAlphaGeometryがGitHubの公式レポジトリで公開されているので、せっかくなので動かしてみます。なお、環境はUbuntu 22.04.3 LTSで実行しています。READMEを参考に以下のように環境を構築して実行してみました。
$ conda create -n alphageometry python=3.10 $ conda activate alphageomety $ git clone [email protected]:google-deepmind/alphageometry.git $ cd alphageometry $ pip install --require-hashes -r requirements.txt
実行に必要なcheckpointなどのダウンロードにはgdownを利用しますので追加でインストールします。
$ conda install -c conda-forge gdown $ gdown --folder https://bit.ly/alphageometry
meliadをインストールします。
$ MELIAD_PATH=meliad_lib/meliad $ mkdir -p $MELIAD_PATH $ git clone https://github.com/google-research/meliad $MELIAD_PATH
こうしてAlphaGeometryの実行の準備はできました。コードに含まれているexamples.txtにはいくつかの例題が記述されています。以下のscript(run.shを元に作成)を実行すれば、記述されている問題をAlphaGeometryで解くことを試すことができます。
#!/usr/bin/bash
DATA=ag_ckpt_vocab
MELIAD_PATH=meliad_lib/meliad
export PYTHONPATH=$PYTHONPATH:$MELIAD_PATH
DDAR_ARGS=(
--defs_file=$(pwd)/defs.txt \
--rules_file=$(pwd)/rules.txt \
);
BATCH_SIZE=2
BEAM_SIZE=2
DEPTH=2
SEARCH_ARGS=(
--beam_size=$BEAM_SIZE
--search_depth=$DEPTH
)
LM_ARGS=(
--ckpt_path=$DATA \
--vocab_path=$DATA/geometry.757.model \
--gin_search_paths=$MELIAD_PATH/transformer/configs \
--gin_file=base_htrans.gin \
--gin_file=size/medium_150M.gin \
--gin_file=options/positions_t5.gin \
--gin_file=options/lr_cosine_decay.gin \
--gin_file=options/seq_1024_nocache.gin \
--gin_file=geometry_150M_generate.gin \
--gin_param=DecoderOnlyLanguageModelGenerate.output_token_losses=True \
--gin_param=TransformerTaskConfig.batch_size=$BATCH_SIZE \
--gin_param=TransformerTaskConfig.sequence_length=128 \
--gin_param=Trainer.restore_state_variables=False
);
python -m alphageometry \
--alsologtostderr \
--problems_file=$(pwd)/examples.txt \
--problem_name=euler \
--mode=alphageometry \
"${DDAR_ARGS[@]}" \
"${SEARCH_ARGS[@]}" \
"${LM_ARGS[@]}"
今回は、eulerを指定しています。具体的なexamples.txtの内容は以下の通りです。
euler a b c = triangle a b c; h = orthocenter a b c; h1 = foot a b c; h2 = foot b c a; h3 = foot c a b; g1 g2 g3 g = centroid g1 g2 g3 g a b c; o = circle a b c ? coll h g o
scriptを実行すると、モデルの準備が始まり、問題を解決するためのログが出力されます。しばらく経つと、以下のような結果とグラフが表示されます。なお、言語モデルの都合上、点の記号は振り直されるので注意が必要です。
========================== * From theorem premises: A B C D H I K L : Points AD ⟂ BC [00] BD ⟂ AC [01] C,H,B are collinear [02] HB = HC [03] A,C,I are collinear [04] IC = IA [05] A,H,K are collinear [06] I,K,B are collinear [07] LB = LC [08] LA = LB [09] * Auxiliary Constructions: J : Points J,A,B are collinear [10] JA = JB [11] * Proof steps: 001. C,H,B are collinear [02] & HB = HC [03] ⇒ H is midpoint of CB [12] 002. A,C,I are collinear [04] & IC = IA [05] ⇒ I is midpoint of CA [13] 003. H is midpoint of CB [12] & I is midpoint of CA [13] ⇒ HI ∥ BA [14] 004. HI ∥ AB [14] & A,H,K are collinear [06] & I,K,B are collinear [07] ⇒ HI:HK = AB:AK [15] 005. J,A,B are collinear [10] & JA = JB [11] ⇒ J is midpoint of BA [16] 006. I is midpoint of CA [13] & J is midpoint of BA [16] ⇒ IJ ∥ CB [17] 007. C,H,B are collinear [02] & C,A,I are collinear [04] & BC ∥ IJ [17] ⇒ ∠HCI = ∠JIA [18] 008. C,A,I are collinear [04] & A,B,J are collinear [10] & AB ∥ HI [14] ⇒ ∠HIC = ∠JAI [19] 009. ∠HCI = ∠JIA [18] & ∠HIC = ∠JAI [19] (Similar Triangles)⇒ IC:AI = IH:AJ [20] 010. AB:AK = HI:HK [15] & IC:AI = IH:AJ [20] & IC = IA [05] & JA = JB [11] ⇒ AB:AK = JB:HK [21] 011. HB = HC [03] & LB = LC [08] ⇒ CB ⟂ HL [22] 012. CB ⟂ HL [22] & AD ⟂ BC [00] & AB ∥ HI [14] ⇒ ∠LHI = ∠DAB [23] 013. LB = LC [08] & LA = LB [09] ⇒ LA = LC [24] 014. IC = IA [05] & LA = LC [24] ⇒ AC ⟂ IL [25] 015. AB ∥ HI [14] & AC ⟂ IL [25] & BD ⟂ AC [01] ⇒ ∠LIH = ∠DBA [26] 016. ∠LHI = ∠DAB [23] & ∠LIH = ∠DBA [26] (Similar Triangles)⇒ LH:HI = DA:AB [27] 017. DA:AB = LH:HI [27] & IC:AI = IH:AJ [20] & IC = IA [05] & JA = JB [11] ⇒ DA:AB = LH:JB [28] 018. AB:AK = JB:HK [21] & DA:AB = LH:JB [28] ⇒ HK:LH = AK:DA [29] 019. A,H,K are collinear [06] & CB ⟂ HL [22] & AD ⟂ BC [00] ⇒ ∠KHL = ∠KAD [30] 020. HK:LH = AK:DA [29] & ∠KHL = ∠KAD [30] (Similar Triangles)⇒ ∠HKL = ∠AKD [31] 021. ∠HKL = ∠AKD [31] & A,H,K are collinear [06] ⇒ KL ∥ DK [32] 022. KL ∥ DK [32] ⇒ L,D,K are collinear ==========================

AlphaGeometryによるexample.txtにある問題(euler)の証明結果
20ステップ以上の推論となる複雑な証明でしたが、無事に\(L\), \(D\), \(K\)が一直線上にあることを証明できました。なお、言語モデルの動作が非決定的であるため、今回の例とは異なる証明とグラフが生成されることもあります。
他にもレポジトリには、IGEX-AG-231という231題の問題のファイルや、実際に論文で議論となったIMO-AG-30の問題ファイルもあって色々と実験できます。また、記号推論エンジン(DD+AR)のみで問題を解くモードもあります(--mode=ddarのオプション)。詳細は公式レポジトリのREADMEを参照してください。これはIMO-2000-p1を証明の例ですが、55ステップもありますが、実は補助線の追加は不要で記号推論エンジンのみで解答されています。
========================== * From theorem premises: A B C D E F G H I J K : Points AC ⟂ AB [00] BA ⟂ DB [01] DE = DB [02] CE = CA [03] DF = DB [04] CF = CA [05] CG = CA [06] GE ∥ AB [07] ∠GAF = ∠GAF [08] DH = DB [09] HE ∥ AB [10] ∠FBH = ∠FBH [11] A,I,G are collinear [12] H,I,B are collinear [13] J,A,F are collinear [14] H,G,J are collinear [15] F,K,B are collinear [16] H,K,G are collinear [17] HK:HF = HK:HF [18] * Auxiliary Constructions: : Points * Proof steps: 001. DF = DB [04] & DH = DB [09] & DE = DB [02] ⇒ H,F,E,B are concyclic [19] 002. H,F,E,B are concyclic [19] ⇒ ∠HEF = ∠HBF [20] 003. H,F,E,B are concyclic [19] ⇒ ∠HFB = ∠HEB [21] 004. H,F,E,B are concyclic [19] ⇒ ∠FHE = ∠FBE [22] 005. CF = CA [05] & CG = CA [06] & CE = CA [03] ⇒ A,E,F,G are concyclic [23] 006. A,E,F,G are concyclic [23] ⇒ ∠FAG = ∠FEG [24] 007. A,I,G are collinear [12] & H,I,B are collinear [13] & ∠HEF = ∠HBF [20] & EH ∥ AB [10] & ∠FAG = ∠FEG [24] & EG ∥ AB [07] ⇒ ∠FAI = ∠FBI [25] 008. ∠FAI = ∠FBI [25] ⇒ A,I,F,B are concyclic [26] 009. A,I,F,B are concyclic [26] ⇒ ∠AFI = ∠ABI [27] 010. A,I,F,B are concyclic [26] ⇒ ∠AIF = ∠ABF [28] 011. DF = DB [04] & DH = DB [09] ⇒ D is the circumcenter of \Delta BFH [29] 012. D is the circumcenter of \Delta BFH [29] & DB ⟂ BA [01] ⇒ ∠HBA = ∠HFB [30] 013. F,K,B are collinear [16] & J,F,A are collinear [14] & ∠AFI = ∠ABI [27] & H,I,B are collinear [13] & ∠HBA = ∠HFB [30] ⇒ ∠HFK = ∠IFJ [31] 014. EG ∥ AB [07] & EH ∥ AB [10] ⇒ EH ∥ EG [32] 015. EH ∥ EG [32] ⇒ H,E,G are collinear [33] 016. CG = CA [06] & CF = CA [05] ⇒ C is the circumcenter of \Delta AGF [34] 017. C is the circumcenter of \Delta AGF [34] & AC ⟂ AB [00] ⇒ ∠GAB = ∠GFA [35] 018. H,E,G are collinear [33] & H,G,J are collinear [15] & ∠GFA = ∠GAB [35] & AB ∥ EG [07] ⇒ ∠GFA = ∠AGJ [36] 019. J,A,F are collinear [14] & ∠GAF = ∠GAF [08] ⇒ ∠GAF = ∠GAJ [37] 020. ∠GFA = ∠AGJ [36] & ∠GAF = ∠GAJ [37] (Similar Triangles)⇒ AG:AF = AJ:AG [38] 021. CF = CA [05] & CE = CA [03] ⇒ C is the circumcenter of \Delta AFE [39] 022. C is the circumcenter of \Delta AFE [39] & AC ⟂ AB [00] ⇒ ∠BAE = ∠AFE [40] 023. ∠AFE = ∠BAE [40] & AB ∥ EG [07] ⇒ ∠AFE = ∠GEA [41] 024. A,E,F,G are concyclic [23] & ∠AFE = ∠GEA [41] ⇒ AE = GA [42] 025. CG = CA [06] & CE = CA [03] ⇒ C is the circumcenter of \Delta AGE [43] 026. C is the circumcenter of \Delta AGE [43] & AC ⟂ AB [00] ⇒ ∠BAG = ∠AEG [44] 027. A,I,G are collinear [12] & ∠BAG = ∠AEG [44] & EG ∥ AB [07] ⇒ ∠IAB = ∠BAE [45] 028. DH = DB [09] & DE = DB [02] ⇒ D is the circumcenter of \Delta BHE [46] 029. D is the circumcenter of \Delta BHE [46] & DB ⟂ BA [01] ⇒ ∠ABH = ∠BEH [47] 030. H,I,B are collinear [13] & ∠ABH = ∠BEH [47] & EH ∥ AB [10] ⇒ ∠IBA = ∠ABE [48] 031. ∠IAB = ∠BAE [45] & ∠IBA = ∠ABE [48] (Similar Triangles)⇒ AI = AE [49] 032. ∠IAB = ∠BAE [45] & ∠IBA = ∠ABE [48] (Similar Triangles)⇒ BI = BE [50] 033. AG:AF = AJ:AG [38] & AE = GA [42] & AI = AE [49] ⇒ AJ:AI = AI:AF [51] 034. J,A,F are collinear [14] & A,I,G are collinear [12] & ∠FAG = ∠FAG [08] ⇒ ∠JAI = ∠FAI [52] 035. AJ:AI = AI:AF [51] & ∠JAI = ∠FAI [52] (Similar Triangles)⇒ ∠AJI = ∠FIA [53] 036. H,E,G are collinear [33] & H,K,G are collinear [17] & F,K,B are collinear [16] & J,F,A are collinear [14] & ∠AJI = ∠FIA [53] & A,I,G are collinear [12] & ∠AIF = ∠ABF [28] & AB ∥ EG [07] ⇒ ∠HKF = ∠IJF [54] 037. ∠HFK = ∠IFJ [31] & ∠HKF = ∠IJF [54] (Similar Triangles)⇒ FI:HF = JI:HK [55] 038. DF = DB [04] & DE = DB [02] ⇒ D is the circumcenter of \Delta BFE [56] 039. D is the circumcenter of \Delta BFE [56] & DB ⟂ BA [01] ⇒ ∠EBA = ∠EFB [57] 040. F,K,B are collinear [16] & ∠EBA = ∠EFB [57] & ∠HFB = ∠HEB [21] & EH ∥ AB [10] ⇒ ∠KFH = ∠EFB [58] 041. H,E,G are collinear [33] & H,K,G are collinear [17] & ∠FHE = ∠FBE [22] & EH ∥ AB [10] & AB ∥ EG [07] ⇒ ∠KHF = ∠EBF [59] 042. ∠KFH = ∠EFB [58] & ∠KHF = ∠EBF [59] (Similar Triangles)⇒ HK:BE = HF:BF [60] 043. H,E,G are collinear [33] & ∠HFB = ∠HBA [30] & AB ∥ EG [07] ⇒ ∠HFB = ∠BHE [61] 044. H,F,E,B are concyclic [19] & ∠HFB = ∠BHE [61] ⇒ HB = BE [62] 045. HK:BE = HF:BF [60] & HB = BE [62] ⇒ HK:HB = HF:FB [63] 046. H,E,G are collinear [33] & H,K,G are collinear [17] & ∠HFB = ∠HBA [30] & AB ∥ EG [07] ⇒ ∠KHB = ∠BFH [64] 047. F,K,B are collinear [16] & ∠FBH = ∠FBH [11] ⇒ ∠KBH = ∠FBH [65] 048. ∠KHB = ∠BFH [64] & ∠KBH = ∠FBH [65] (Similar Triangles)⇒ BK:BH = BH:BF [66] 049. BK:BH = BH:BF [66] & BI = BE [50] & HB = BE [62] ⇒ BK:BI = BI:BF [67] 050. F,K,B are collinear [16] & H,I,B are collinear [13] & ∠FBH = ∠FBH [11] ⇒ ∠KBI = ∠FBI [68] 051. BK:BI = BI:BF [67] & ∠KBI = ∠FBI [68] (Similar Triangles)⇒ IB:IK = FB:FI [69] 052. FB:FI = IB:IK [69] & HB = BE [62] & BI = BE [50] ⇒ FB:FI = HB:IK [70] 053. HK:HB = HF:FB [63] & FB:FI = HB:IK [70] ⇒ FI:HF = IK:HK [71] 054. FI:HF = JI:HK [55] & FI:HF = IK:HK [71] ⇒ IK:HK = JI:HK [72] 055. IK:HK = JI:HK [72] & HK:HF = HK:HF [18] ⇒ IK = JI ==========================

AlphaGeometryによるIMO 2000 P1の証明結果
まとめ
さて、AlphaGeometryについて、ざっくりと解説とデモを紹介しました。LLMの苦手とする正確な推論を補完するために、それ専用の記号推論エンジンを組み合わせるという点が興味深いです。論文のExtended Data Table 3には、今回のようなアプローチで幾何学以外にも適応できる可能性がある数学分野が紹介されています。数学の問題解決には、今回の幾何学のような“補助線”(auxiliary construction)を閃くことが鍵となります。例えば、こちらの表にも有名な素数の個数が無限個であることの証明があります。証明のステップ2で導入する新しい数 \(p\) が、問題解決のポイントとなります。
- 素数の数が有限個と仮定 (\(p_1, p_2, \dots, p_n\))
- すべての素数の積に1を加えた数 \(p = p_1 p_2 \cdots p_n + 1\) を導入
- \(p \) は、既知のどの素数(\(p_1, p_2, \dots, p_n\))でも割ることができないので素数
- \(p \) は、(\(p_1, p_2, \dots, p_n\)) に含まれないので素数ではない
- 3と4の結論は矛盾する。従って最初の仮定1が間違いで、素数は無限個存在する
AlphaGeometryの場合、幾何学に関してはDD+ARの推論エンジンが効率的に機能していますが、他の分野に関しては、また別のアプローチが必要となるので、今後の研究の進捗を期待したいところです。
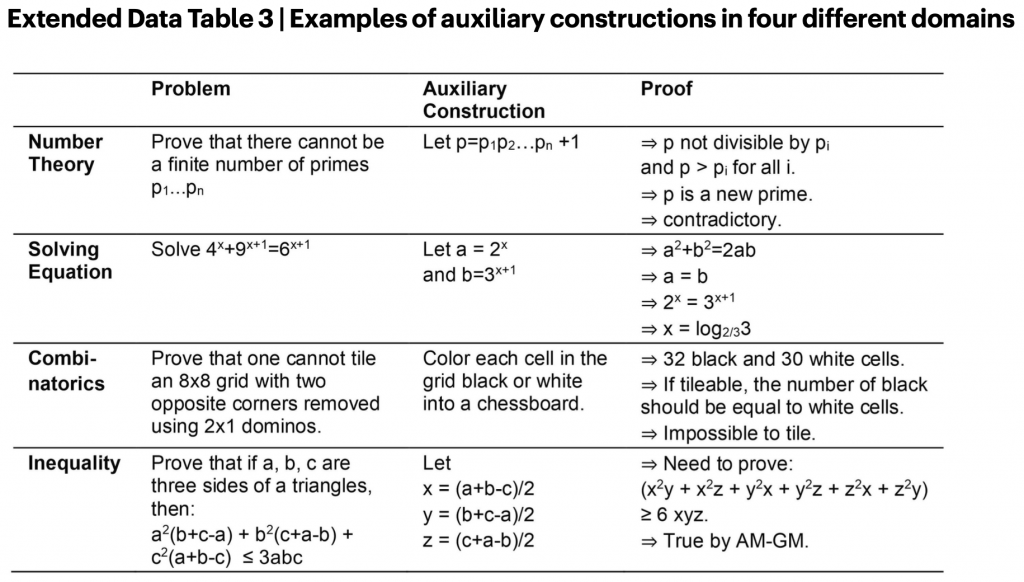
AlphaGeometryと同様のアプローチを幾何学以外の数学分野への応用例(AlphaGeometryの論文より)
また、AlphaGeometryは、問題を解くことに特化したある種の計算機です。学習のために10億個ものランダムな前提から定理を生成したものの、その殆どが数ステップで示せる比較的簡単な定理であったことを考えると、問題を発見する・適切な問題を提案するという点において、まだまだ、AIの限界があると言えるかもしれません。プロ棋士が将棋AIを活用して新たな戦術を発見するように、将来的には、数学者がこの種のAIを数学の研究に活用する日が来るかもしれません。
グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。
参考資料
- Google DeepMind AlphaGeometry: An Olympiad-level AI system for geometry [https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry/]
- AlphaGeometry GitHub [https://github.com/google-deepmind/alphageometry]
- Nature “Solving olympiad geometry without human demonstrations” [https://www.nature.com/articles/s41586-023-06747-5]
- Nature 注目のハイライト(2024年1月18日)「計算機科学:AIは数学の超難問にも対応できるようになった」 [https://www.natureasia.com/ja-jp/nature/pr-highlights/14769]
- International Mathematical Olympiad [https://www.imo-official.org/]
- 数学オリンピック財団 [https://www.imojp.org/index.html]
- ダニエル・カーネマン「ファスト&スロー(上・下)あなたの意思はどのように決まるか?」[https://www.hayakawa-online.co.jp/product/books/90410.html]
- IJCAI2021 Invited Talks, Yoshua Bengio “System 2 Deep Learning: Higher-Level Cognition, Agency, Out-of-Distribution Generalization and Causality” [https://ijcai-21.org/invited-talks/]
- Gröbner基底 [wikipedia]
- Wu’s method of characteristic set
[wikipedia]
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD