外れ値がt検定に与える影響の実験

まとめ

• 裾の重い分布において、外れ値の処理をせずにt検定することが「サンプルの偏りによって第一種の過誤を誘発する」のか、逆に「分散が大きくなり検出力の低下を誘発する」のかを検証した。

• どちらも基本的には誘発しない。また、極端に裾が重いパレート分布やコーシー分布は検出力の低下を誘発する。

こんにちは、M.S.です。ABテストを行う上で厄介なものに“外れ値”があります。

これまでABテストを実施してきて２標本のt検定で効果検証を進めてきた方も多いでしょう。しかし、売上のように本来の分布が裾が重い分布を持つメトリクスでは、数件の極端に大きな値が結果全体を歪めることがあります。たとえばECサイトのように、ほとんどのユーザは少額購入なのに、まれに巨大なカートで一気に数十万円・数百万円を購入するケースが発生する……。このように「外れ値」と呼ばれる一見“まれ”な観測値は、実はビジネスでは意外に頻繁に起こり得るものです。ここでは、そんな外れ値がABテストにどのような影響を与えるのか、そしてその対処法を中心に考えてみたいと思います。

1. t-test とその前提条件

t-test（ここでは二群の平均値を比較する「対応のない t-test」または「二標本 t-test」を想定）は、以下のような前提や仮定が存在します。

1. 各グループの母集団が正規分布に近いこと
   t-test は、サンプルサイズが十分大きい場合に中心極限定理によって正規性の仮定がある程度緩和されるとはいえ、理論的には「母集団が正規分布に従う」ことが基本的な前提です。

2. 外れ値の影響
   t-test は平均値ベースで検定を行うため、外れ値（極端に大きい観測値や小さい観測値）の影響を受けやすい手法です。とくに重尾分布では外れ値が頻繁に出現するため、分散が過大に推定されたり平均値が大きく振られたりしてしまう可能性があります。

3. 分散の等質性
   Welch の t-test など一部の手法では異なる分散を許容しますが、通常の t-test では分散の等質性を仮定することも多いです。重尾分布においては群間で分散が大きく異なることが多く、この条件を満たしにくいケースが多々あります。

2. 裾の重い分布 (Heavy-tailed distribution) の特徴

売上や収益などのビジネス指標は、しばしば非常に小さい値が多数観測される一方で、極端に大きい少数の値が観測されることがあります。これが「裾の重い分布」と呼ばれるもので、代表的な例として以下が挙げられます。

• パレート分布

• 対数正規分布

• 極端に歪んだガンマ分布 など

こうした分布では「外れ値（outlier）」と見えるような大きな値が珍しくなく、その存在が分析結果や統計推定値を大きく動かします。

3.裾の重い分布が t-test に与える影響

1. 平均値と分散の推定の歪み
   外れ値があると、平均値や分散が過大に推定される傾向にあります。t-test は群間の「平均値の差」を検定する手法ですから、分散推定が膨らむほど検定統計量の値は小さくなり、有意差が検出されにくく（Type II エラーのリスク増大）なります。また外れ値によって平均値が振られてしまうと、そもそも意味のある比較ができない可能性もあります。

2. 正規性の仮定違反
   t-test はサンプルサイズが十分大きければ中心極限定理によりある程度正規性の前提が緩和されるものの、裾の重い分布における外れ値が極端に大きい場合、この前提の「近似的な正規性」自体が損なわれる可能性があります。特にサンプルサイズが小さい場合は、正規分布からの逸脱が大きく影響します。

3. 分散の不均一性
   裾の重い分布をとるデータは、外れ値の頻度や大きさが異なることで、AB テストの比較群ごとに分散が大きく異なることがあります。分散が著しく異なる場合、分散の等質性を仮定する t-test では問題が起こりやすいです。Welch の t-test でも、分散の推定が膨らむと前述の通り統計量が小さくなる問題が残ります。

4. 信頼区間の解釈
   平均値を重視した検定や推定では、信頼区間の幅が外れ値によって過剰に広がることがあります。例えば売上のように「ごく少数の大きな値」が平均を大きく動かすケースでは、平均値自体の推定精度が低下し、信頼区間が膨らみやすくなります。そのため、結果解釈が困難になったり、最終的な意思決定に迷いが生じる場合があります。

4.クエスチョン

データ分析をする上で、外れ値（outliers）の存在は常に議論の的になります。ときに「外れ値をそのまま含めると外れ値が一方の群に偏ったときに、誤って差ありと判定してしまう（第一種の過誤を増やす）」と聞く一方で、「外れ値があると分散が大きくなり、むしろ差を見つけにくくなる（検出力を下げる）」という主張も耳にします。はたして外れ値は本当にどちらの方向に働くのでしょうか。それとも、実はあまり影響しないのでしょうか。

本稿では、「外れ値は検定力（有意差検出力）をどのように変化させるのか」という論点にフォーカスします。いわば外れ値が第一種の過誤（偽陽性）を高めるのか、それとも有意差を見逃しやすくするのかをシミュレーションを通じて検証します。特に、

• 裾の重い分布の差異（パレート分布や対数正規分布など）

• サンプルサイズの大小

といった条件ごとに外れ値が t 検定に与える影響を観察し、どの程度「有意差がないのに有意差が出てしまう」あるいは「有意差があるのに検出できない」事態が生じるのかを明らかにします。結果として、「外れ値は自分が考えている方向とは真逆の影響を与えうる」ケースもありうることが示されるかもしれません。

方法

ポイント

ポイントとしては同じ分布から無作為抽出によって、２つのグループを作りttestをするということを繰り返した際に、理想的にはp値が一様分布に近づくはずだが、裾の重い分布・外れ値の影響によって「特定の領域に偏る」ケースが起こります。その偏り方によって、次の 2 つのパターンをざっくり見分けられます。

1. p 値が 0 に近い領域に偏る

   • p 値が小さいほど「帰無仮説棄却（有意差あり）」と判定されやすい

   • 帰無仮説が真なのに p 値が小さくなる頻度が高い → 偽陽性（Type I エラー）が増えている

   • すなわち、検定が“攻撃的”になり、差がないのに「差がある」と誤ってしまう傾向

2. p 値が 1 に近い領域に偏る

   • p 値が大きいほど「差がない」と判定されやすい

   • 本来 0～1 の間で均等に出るはずが、高い領域に集中している → 多くの場合「分散が大きく推定され、検定統計量が小さくなる」方向

   • 有意差があっても検出できない（＝検出力の低下）、あるいは「偽陽性が規定より少ない」（保守的）という捉え方もできる

具体的な方法

1. 検証観点
   本検証では、以下の 2 つの観点 から外れ値の影響を調べる。

   1. (A) 分布ごとの差

      • パレート、対数正規、ガンマ、正規分布（比較対象）など、複数の母集団（裾の重さが異なる分布）を設定。

      • それぞれから A 群・B 群を「同じパラメータ」でサンプリングし、t 検定を行った際の p 値を比較する。

   2. (B) サンプルサイズの大小

      • 各分布についてサンプルサイズを 10, 100, 1000, … と大きく変化させ、外れ値の影響がサンプルサイズによってどう変わるかを確かめる。

2. データ生成

   1. (A) 分布比較

      • たとえばパレート分布、対数正規分布、ガンマ分布、正規分布などを用意。

      • 同じパラメータで A 群・B 群を生成し、「差がない（帰無仮説が真）」状態を作る。

   2. (B) サンプルサイズ比較

      • 上記分布別に、サンプルサイズを n=10, 100, 1000, … に変えて同様のシミュレーションを行う。

      • 少数標本ほど外れ値の影響が大きくなるか、あるいは分散が膨らむ方向になるかを実験的に検証する。

3. 統計検定

   • 各シミュレーションで A 群・B 群のサンプルを取得 → Welch の t 検定 (equal_var=False) → p 値を算出。

   • 帰無仮説が真なので、本来 p < 0.05 となる確率は 5% 前後が理想的だが、裾の重い分布の外れ値によって「有意差が出やすい・出にくい」どちらに転ぶかを観察する。

4. シミュレーションと可視化

   • 1 回のシミュレーションで (1) データ生成 → (2) t 検定 → (3) p 値を保存、という工程を行い、これを 2,000 回 など多数回繰り返して p 値の分布を得る。

   • p 値のヒストグラム を描画し、p 値が 0～1 のどこに偏るかを確認するとともに、p < 0.05 の割合（= Type I エラー率） を算出。5% との乖離状況をチェックする。

   • (A) で分布ごとにヒストグラム・偽陽性率を並べて比較する。

   • (B) でサンプルサイズ n=10, 100, 1000… ごとにヒストグラムを並べ、外れ値の影響がどう変わるかを把握する。

コード例

（A）の検証

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind
from scipy.stats import pareto, gamma, cauchy  # cauchyはalpha=1 stableの一例
from statsmodels.distributions.empirical_distribution import ECDF

np.random.seed(42)

def generate_lognormal(size, mu=0.0, sigma=1.0):
    return np.exp(np.random.normal(loc=mu, scale=sigma, size=size))

def generate_pareto(size, x_m=1.0, alpha=1.5):
    # SciPyのpareto分布は、CDF: 1 - (1/x)^alpha, x >= 1
    # ここでスケール= x_m, 形状= alphaに対応
    # => random変数は x_m * (1 + R)^1/alpha の形で生成される。
    # scipy.stats.pareto.pdf(x, alpha) はx>=1
    return x_m * pareto.rvs(alpha, size=size)

def generate_gamma(size, shape=2.0, scale=1.0):
    return gamma.rvs(shape, scale=scale, size=size)

def generate_alpha_stable(size, alpha=1.2, beta=0, scale=1.0, loc=0.0):
    """
    SciPyにはalpha-stableの直接乱数生成はありませんが、
    例としてalpha=1 (Cauchy)はscipy.stats.cauchyで生成可能。
    alpha=1.2 等、汎用的には外部ライブラリや自前実装が必要。
    ここではイメージとして cauchy (alpha=1) を例にします。
    """
    if alpha == 1.0:
        # Cauchy
        return cauchy.rvs(loc=loc, scale=scale, size=size)
    else:
        raise NotImplementedError("alpha-stable for alpha != 1 not directly in SciPy")

# --- 分布のリストを定義 ---
distributions = {
    "Normal(0,1)": lambda n: np.random.normal(0, 1, n),
    "Lognormal(mu=0, sigma=1)": lambda n: generate_lognormal(n, mu=0, sigma=1),
    "Pareto(x_m=1, alpha=1.5)": lambda n: generate_pareto(n, x_m=1.0, alpha=1.5),
    "Gamma(k=2, scale=2)": lambda n: generate_gamma(n, shape=2.0, scale=2.0),
    "Cauchy(alpha=1 stable)": lambda n: generate_alpha_stable(n, alpha=1.0, scale=1.0)
}

alpha_level = 0.05
n_sim = 2000       # シミュレーション回数
n_samples = 50     # 各群のサンプルサイズ

results = {}

for dist_name, dist_func in distributions.items():
    count_type1 = 0
    pvals = []
    for _ in range(n_sim):
        # A群, B群は全く同じ母集団(同分布)から生成
        groupA = dist_func(n_samples)
        groupB = dist_func(n_samples)

        # Welchのt検定 (分散不等を想定)
        _, p = ttest_ind(groupA, groupB, equal_var=False)
        pvals.append(p)

        if p < alpha_level:
            count_type1 += 1

    # 偽陽性率
    false_positive_rate = count_type1 / n_sim
    results[dist_name] = {
        "mean_pval": np.mean(pvals),
        "median_pval": np.median(pvals),
        "type1_error": false_positive_rate,
        "pvals": pvals
    }

# --- 結果を表示 ---
for dist_name, info in results.items():
    print(f"{dist_name}: ")
    print(f"  Type I Error Rate = {info['type1_error']*100:.2f}% (ideal=5%)")
    print(f"  Mean p-value      = {info['mean_pval']:.3f}")
    print(f"  Median p-value    = {info['median_pval']:.3f}")
    print("")

# --- p-value分布を簡易可視化 ---
plt.figure(figsize=(10,6))
for i, (dist_name, info) in enumerate(results.items()):
    plt.subplot(2,3,i+1)
    plt.hist(info['pvals'], bins=30, range=(0,1), edgecolor='black')
    plt.title(dist_name)
    plt.ylim([0, n_sim//3])  # 見やすく
    plt.xlabel("p-value")
    plt.ylabel("Freq")
plt.tight_layout()
plt.show()

（B）の検証

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind, pareto

np.random.seed(42)

def generate_pareto(size, x_m=1.0, alpha=1.5):
    """
    Pareto分布に従う乱数を生成する関数。
    scipy.stats.pareto は x >= 1 で定義される形状を用いるため、
    x_m (scale) を掛けてスケーリングする。
    """
    return x_m * pareto.rvs(alpha, size=size)

# --- パラメータ設定 ---
alpha_level = 0.05                  # 有意水準
n_sim = 2000                        # シミュレーション回数
pareto_xm = 1.0                     # パレート分布のスケールパラメータ
pareto_alpha = 1.5                  # パレート分布の形状パラメータ(重尾度)
sample_sizes = [10, 100, 1000, 10000, 100000,]  # 各グループのサンプルサイズリスト

# --- 結果を格納する辞書。 { n: [p_values], ... } の形 ---
pvals_dict = {}

for n in sample_sizes:
    p_vals = []
    for _ in range(n_sim):
        # A群、B群を同じパラメータのパレート分布から生成
        groupA = generate_pareto(n, x_m=pareto_xm, alpha=pareto_alpha)
        groupB = generate_pareto(n, x_m=pareto_xm, alpha=pareto_alpha)
        
        # Welchのt検定
        _, p = ttest_ind(groupA, groupB, equal_var=False)
        p_vals.append(p)
    
    pvals_dict[n] = np.array(p_vals)

# --- プロット: p値のヒストグラム (サンプルサイズ毎) ---
plt.figure(figsize=(12, 8))

for i, n in enumerate(sample_sizes, start=1):
    p_values = pvals_dict[n]
    # 偽陽性率（p < alpha_level の割合）
    type1_error = (p_values < alpha_level).mean()
    
    # subplot
    plt.subplot(2, 3, i)
    plt.hist(p_values, bins=30, range=(0,1), edgecolor='black')
    plt.title(f"n={n}\nType I error={type1_error:.3f}")
    plt.xlabel("p-value")
    plt.ylabel("Freq")

plt.tight_layout()
plt.show()

結果

(A) 分布比較

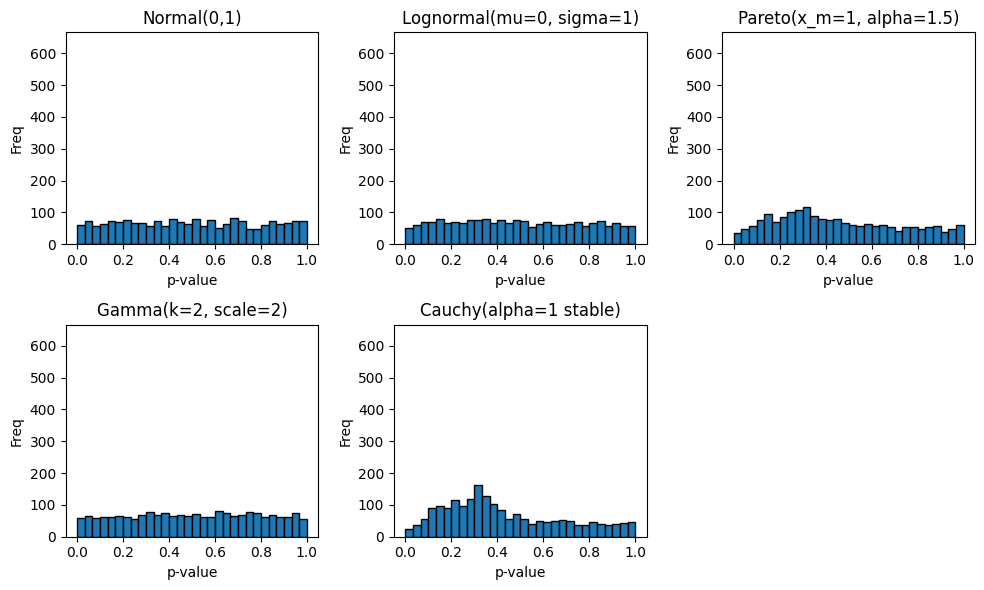
こちらは様々な分布から無作為抽出をした二群をt検定したときのp値の分布です。

グラフを見るかぎり、「正規分布」では p 値が 0～1 の範囲でほぼ均等に広がっている（＝理論通り一様分布に近い）のに対し、裾が特に重い分布（とくにパレート分布やコーシー分布など）では p 値がやや高め（0.2~0.4にくらいに最頻値がある)で明らかに一様分布とは異なる形状になっているのが見て取れます。

ここから、言えることは２点あり、

・裾が重い分布は、p<0.05となる確率が0.05より小さくなるので有意差があっても検出できない（＝検出力の低下）保守的な結果となりやすい。逆に第一種の過誤が高くなるということはない。

・その傾向は、分布によって特徴が異なる。特に、今回は正規分布・対数正規分布・ガンマ分布のような指数関数的に0に近づいていく確率密度関数のグループとパレート分布やコーシー分布のような多項式関数的に0に近づいていく確率密度関数のグループで傾向が分かれた。指数関数的に0に近づいていくような分布の性質はそもそも理想的な性質を持っている可能性があります。

(B) サンプルサイズ比較

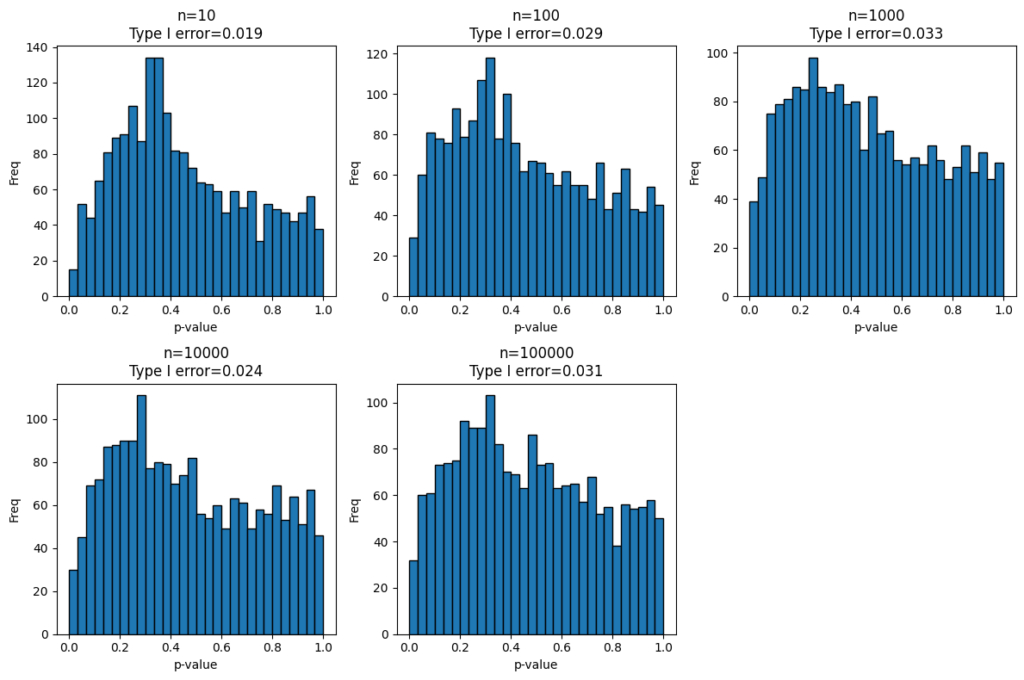
こちらは（A）の実験で分布に特徴があったパレート分布に限定してサンプルサイズを変化させたときのp値の分布です。

基本的に分布の形状は大きく変わらず、0.2~0.4にピークがあります。このため、サンプルサイズが小さいときに外れ値の影響を受けて、p<0.05の領域に偏るということはなさそうです。

ただし、このあたりは、母集団から無作為抽出をするのではなく、既存の標本から無作為分割をして２グループを作るという現実的な方法でサンプルを作成した場合は違う結果になるかもしれませんね。

まとめ

• 外れ値を処理しない→ 分散過大推定 → 検定力（パワー）が下がる傾向

そこで有意差が出ない場合は、外れ値の処理（clipや切り捨て）や、順位和検定を行う、混合分布としてパラメタを推定するといった検出力の高い方法で二段階の評価を行って総体的な判断を行うのが良いのではないかと思います。ただし、このような二段階で検定を行うことは、多重検定の問題があり、分析官が総合的に判断をする必要があるでしょう。

最後に

グループ研究開発本部 AI 研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務など AI 研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。