2016.04.07
Experiments on popular parameter optimization methods used in neural network
次世代システム研究室のL.G.Wです。今回はニューラルネットワークによく使われるパラメータ最適化アルゴリズムについて紹介させていただきます。
アルゴリズムの実装から比較結果まで一通り解説します。ニューラルネットワークにおけるOptimization手法により、パラメータがどう最適化解に辿り着いたかを可視化しました。
Introduction
In this blog post, I would like to share some experimental results about an array of parameter optimization methods widely used in neural network. When I am learning an online deep learning course provided by Stanford Univ. (namely Stanford CS231n), I found it is very interesting and helpful to visualize how the parameters are optimized, in order to grasp what happened in deep neural network (called DNN) and how it works. Next I will elaborate what i did and what i found for that.
The basic architecture of deep neural network is shown in the following figure:
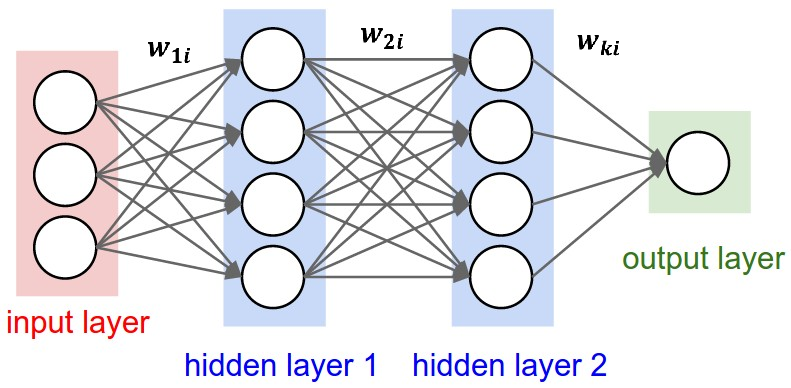
From the input to output, there are a huge amount of parameters applied for feature transformation. In deep neural network, the training process is exactly equal to exploring the best parameters which achieves the least error (or loss) at the side of output by a given input.
Moreover, in my opinion, the deep neural network (not including recurrent neural network) can be simplified as the following formula:
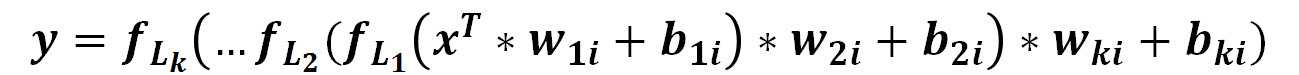
Given an input X, and transform the input with parameters through operations such as convolution, activation and down sampling, finally get an output (Note that in some layers (e.g. down sampling or activation) parameters are considered as a constant (0 or 1)). As you can see, the fundamental problem in DNN is how to optimize these parameters. Also it is crucial to the accuracy and computation performance. This is also why I want to explore the parameter optimization methods.
Optimization methods
Basically there are two approaches to optimize or estimate the parameters: analytical optimization and numerical optimization.
The former is fast (no iteration is needed if the analytical gradient is solved) and it can get the exact optimal result, however it usually requires a inverse Hessian matrix (in view of quadratic form of the loss) which is prohibitively computation intensive especially when handling massive parameters, and analytical methods (the analytical gradient) is not solvable in some cases. Doubtlessly, it is very effective in some cases, mostly applied in Maximum Likelihood Estimation (MLE) and Maximum A Posterior (MAP).
On the other hand, numerical optimization always can obtain an optimal result yet it may be not a global optimal. Numerical optimization usually involves an iterative process, which slowly estimate the parameters to converge. In deep neural network, it is common to use the latter (numerical methods).
There are also a series of numerical (approximation) methods used in machine learning, including Bayesian Estimation, Expectation Maximization (EM), Variational Inference and sampling methods (such as MCMC and Gibbs sampling). However, these methods are not used in DNN (yet some researchers tried MCMC). Why not? I didn’t do a comprehensive survey, but just according to my intuition, they are probably not effective due to these two reasons: the huge number of parameters and the back propagation mechanism (to estimate layered parameters).
In fact, the popular optimization methods used in DNN is another kind of numerical optimization called gradient based methods or exhaustive search methods. (Yes, it is brutal, not intelligent). The typical one is SGD (Stochastic Gradient Descent). Based on SGD, there are several variants (or improvements), including Momentum, Nesterov Accelerated Gradient (NAG, see [Bengio et al., 2012]), AdaGrad (see [Duchi et al., 2011]), RMSProp (see [Tieleman and Hinton, 2012]) and Adam (see [Kingma and Ba, 2014]).
All these methods are implemented in the mainstream deep learning frameworks (including Tensorflow, Caffe, Torch and Chainer). In our experiments, we implemented these six methods and compared their performance.
Implementation
The source is uploaded to Git Hub (here).
Here I will explain main points of the source.
- Neural Network
- Parameter Optimizer
- SGD
- Momentum
- Nesterov Accelerated Gradient (NAG)
- AdaGrad
- RMSProp
- Adam
- Visualization
- Test Stage
Since our purpose is to explore parameter optimization, I developed a shallow neural network (one layer only).
Without loss of generality, here we only tried one activation function – sigmoid().
The loss (we use cross entropy) is calculated in the function forward() which also take parameter regularization into account. The gradient is calculated in the function gradient(). In our case the local gradient is equal to global gradient since our NN is single layer.
The function mapFeature() expands 2-dimensional features to N-dimensional space, therefore we can observe N parameters.
Note that we added a constant 1 to features so that the first parameter is the bias parameter.
The following optimization methods are implemented.
The basic idea behind SGD (Stochastic Gradient Descent) is to search parameter space following the gradient. But it is very slow along flat direction, while jitters along steep one due to quickly changing sign.
Based on SGD, Momentum adds a parameter (called mu) which works as the friction coefficient during searching. This parameter (mu) can speed up searching along shallow directions, while speed down searching in deep direction nearby the optimal so that it can avoid or mitigate jitters.
NAG is a bit different from Momentum by slightly changing the direction of gradient. The following figure (source from Standford CS231n) shows the difference between Momentum and NAG.
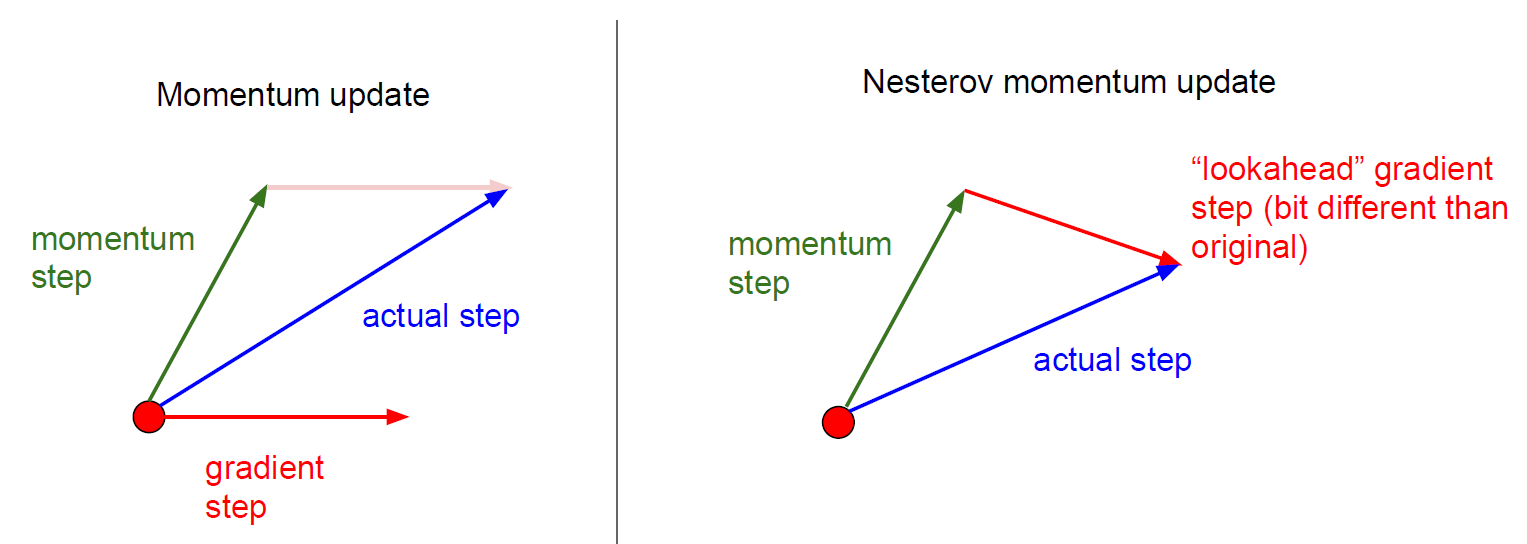
AdaGrad adds element-wise scaling of the gradient based on the historical sum of squares in each dimension, meaning that the searching speed will slow down along with iteration and keeps different learning speed in each dimension.
RMSProp is an improved version of AdaGrad, which puts priority on the recent gradients instead of summing up all historical gradients.
Adam can be considered as the combination of Momentum and RMSProp. That is, it takes both the first moment and the second moment of gradients into account.
To train the data for parameter optimization (see train()), we simply execute a full batch instead of mini-batch widely used in real application because we only input a small amount of data in our experiments. In addition, we preserve the option to adjust the convergence condition: loss tolerance or parameter tolerance.
We plot two graphs to observe the convergence performance. One is the loss along with the iteration times, another one is how the parameters converge to the optimal in a plate.
In test stage, you can generate random training data or use the data provided by Andrew Ng’s Course.
You also can try other optimization methods provided by R, including BFGS and L-BFGS-B which approximates a inverse Hessian matrix to get analytic gradient.
Experimental result and discussion
We compared the converge performance over all methods including our implemented methods and other two methods provided by R package.
The result is summarized as the following table:
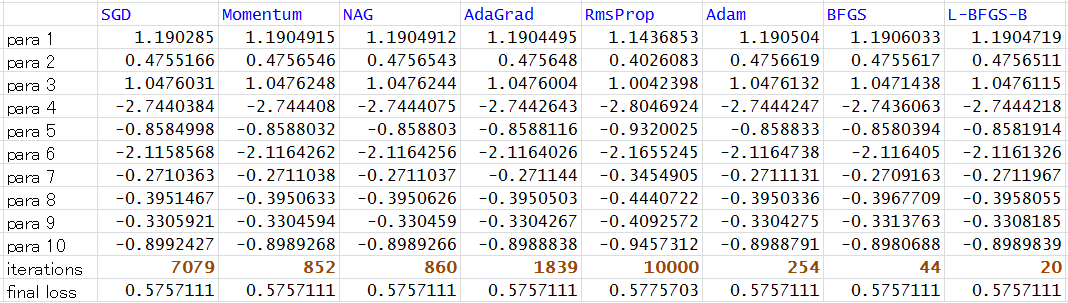
We can see from the above table, all methods except RmsProp are converged (see final loss and iterations). The fastest ones are BFGS and L-BFGS-B (the number of iterations is the least). Among our implemented methods, Adam performs the best.
The following figure is plotted by our visualization method. It shows the loss over iteration times (epoch) but we cut off the late iterations.
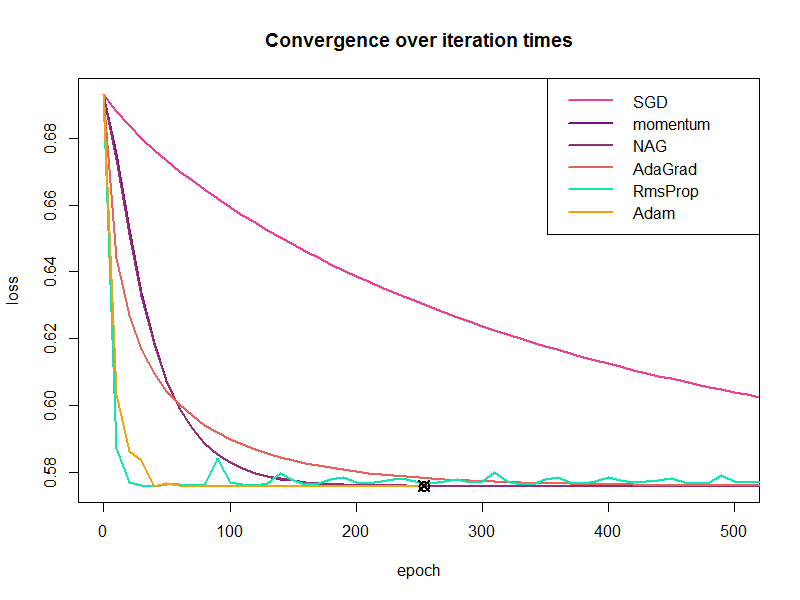
We found (from the above figure) that (1) Adam converges very quickly, (2) SGD converges very slowly but steadily, (3) Momentum and NAG performs almost the same and much better than SGD, (4) AdaGrad performs a bit better than Momentum and NAG, (5) RmsProp is pretty weird, it converges very quickly at the early stage but it doesn’t converge at late stage (sometimes the loss reverts).
We also plotted how the parameters (any two parameters) converge in the 2-dimensional space as shown in the following figure:
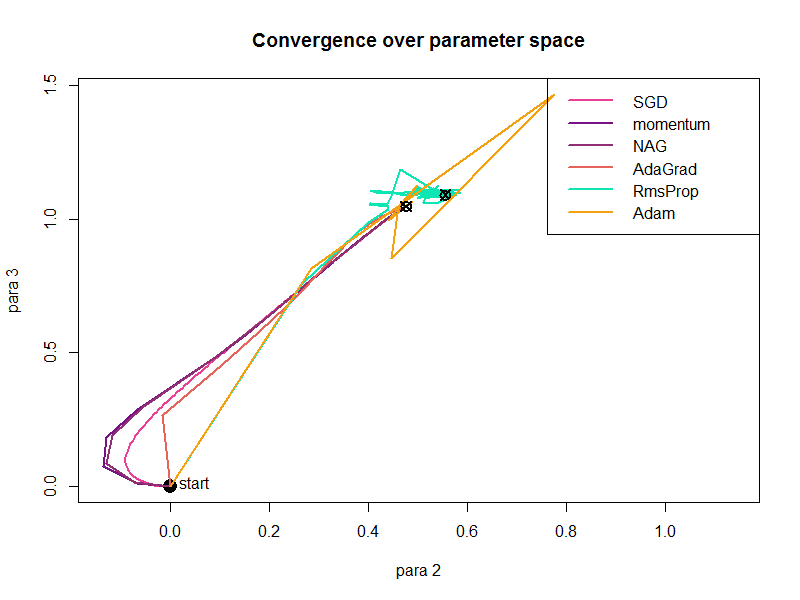
It shows that (1) Adam approaches the final point (the optimal) directly at first but then takes a detour when close to the final, (2) RmsProp behaves similarly to Adam, but finally doesn’t converge to the optimal, (3) other four methods converge in a similar way.
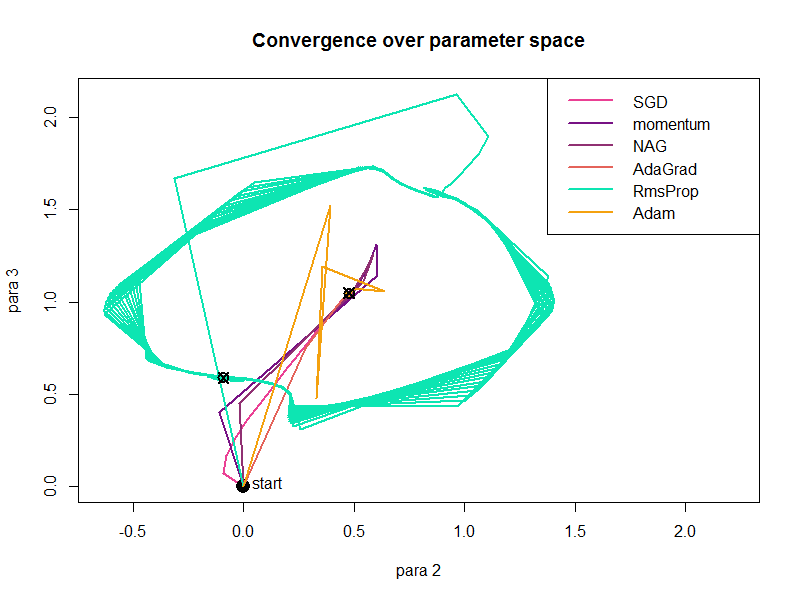
We also evaluated how the learning rate affects the convergence method. When changing the learning rate, some methods perform better while other methods perform worse. Moreover, we found Adagrad performs the best in some cases. The following figure shows the convergence after increasing the learning rate. It shows the RmsProp performs very strangely (Even i doubt i incorrectly implemented the algorithm).
We also studied how other factors affect the convergence, e.g., parameter initialization, parameter number (dimensions), different data samples, and so on. I will introduce in the next blog in future. (You also can play with them as i have uploaded the full source).
Conclusion and future work
In conclusion, we can roughly say that Adam and Adagrad perform better than other methods in most cases. Moreover, convergence speed is affected by different factors, especially by the learning rate. I hope this blog can help you understand neural work more deeply and comprehensively, although i didn’t simulate the deep neural network. (Maybe methods perform different in multi-layer NN.)
In future, i plan to develop a deep neural network, and visualize the convergence over parameter space by animation.
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD