2023.01.12
表形式データに特化するDiffusion Modelの紹介
こんにちは。次世代システム研究室のA.Z.です。
前回のブログでは簡単にDiffusionモデルの紹介と一般的な応用分野(画像生成)について話しました。今回はもっと違うデータの形の応用でについて簡単に紹介したいと思います。
はじめに
Diffusionモデルは生成モデルとしての応用は画像系の生成分野に圧倒的に性能がよく、幅広くよく知られています。画像系の分野(コンピュータビジョン)の分野以外でも、応用実績多数があります。例えば、最新のDiffusionモデルのサーベイ論文では様々な応用の例が紹介されました。
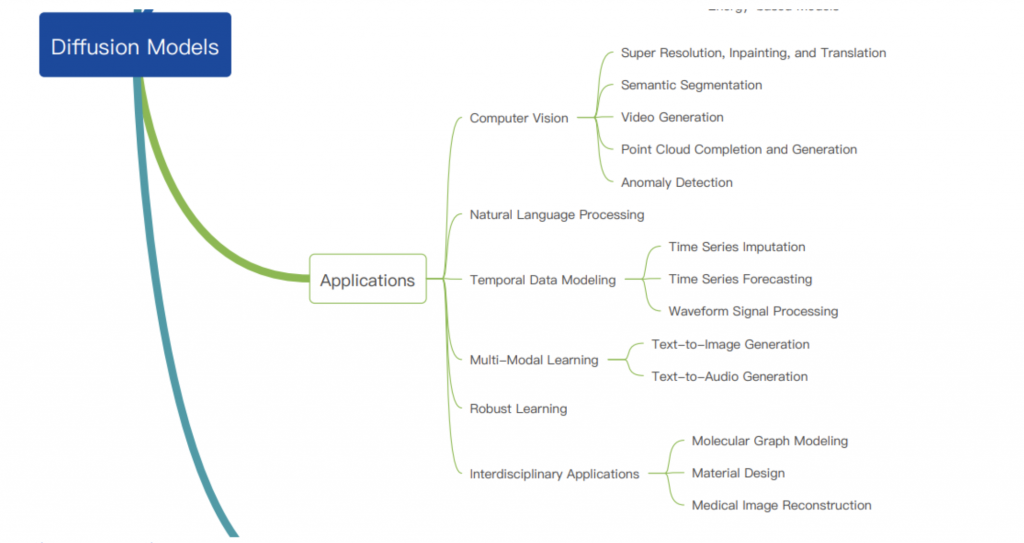
引用:https://arxiv.org/pdf/2209.00796.pdf
上記から、Diffusionモデルは幅広い分野の応用の実績を持ち、これからの更に発展すると期待されています。
現在、私がかわかっているプロジェクトに、一部Diffusionモデルを入れると検討しています。画像や自然言語処理用データがありますが、場面やユースケースケースがかなり限られて、導入に対するの効果がそこまで大きくないと思います。ただし、表形式(tabular)のデータが圧倒的に多く、活用の場面やユースケースが幅広く、導入に対する効果が大きいと思われます。また、表形式データが、ビジネスの世界の中に、一番一般的になり、
他のプロジェクトにも応用した場合は得たKnow-Howが横展開できます。
今回は表形式のデータに特化した、Diffusionモデル(TabDDPM)を詳しく話したいと思います。
TabDDPM: Denoising Diffusion Probabilistic models (DDPM) for Tabular dataの紹介
今回紹介したいのは、表形式データに特化したDiffusion モデル(TabDDPM)のことです。
https://arxiv.org/pdf/2209.15421.pdf
https://github.com/rotot0/tab-ddpm
表形式のデータは画像と自然言語のデータと違って、複数の特徴量で構成され、それぞれの特徴量の関連性が不明なときに多いです。また、複数種類の特徴量が合成されることが多く、diffusionモデルの応用には工夫が必要です。
一番一般的な表形式データでは、「数字」と「カテゴリ」の特徴量のタイプがあり、TabDDPMは「数字」特徴量をまとめてGaussian Diffusionを行います。「カテゴリ」の特徴量の場合は、各特徴量に対して、別々のDiffusionプロセスを行い、Multinomial Diffusionのメソッドを使っています。Noiseから、元のデータに復元する(Reverse)プロセスにはシンプルなMulti Layer Perceptron(MLP)のアーキテクチャを使っています。
具体的なネットワークの構造や前処理などは以下になります。
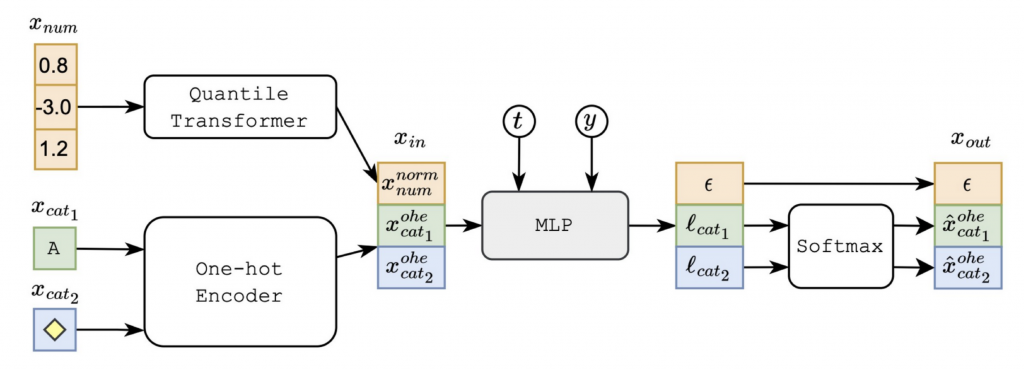
引用:https://arxiv.org/pdf/2209.15421.pdf
では、次は、モデルの部分で、重要な部分をピックアップし、詳細を紹介します。
Reverse Diffusionのモデル (MLPモデル)
論文の中には、MLP詳細のアーキテクチャは書かれていないですが、実際に、コードで動かしてみて、詳細のモデルの構造は以下になります。
MLPDiffusion(
(mlp): MLP(
(blocks): ModuleList(
(0): Block(
(linear): Linear(in_features=128, out_features=512, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
(1): Block(
(linear): Linear(in_features=512, out_features=1024, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
(2): Block(
(linear): Linear(in_features=1024, out_features=1024, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
(3): Block(
(linear): Linear(in_features=1024, out_features=1024, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
(4): Block(
(linear): Linear(in_features=1024, out_features=1024, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
(5): Block(
(linear): Linear(in_features=1024, out_features=512, bias=True)
(activation): ReLU()
(dropout): Dropout(p=0.0, inplace=False)
)
)
(head): Linear(in_features=512, out_features=16, bias=True)
)
(label_emb): Embedding(2, 128)
(proj): Linear(in_features=16, out_features=128, bias=True)
(time_embed): Sequential(
(0): Linear(in_features=128, out_features=128, bias=True)
(1): SiLU()
(2): Linear(in_features=128, out_features=128, bias=True)
)
)
MLPの部分は6層ほど組み合わせになり、ごく一般的な活性化関す(ReLu)と安定化(Dropout)と組み合わせなります。
label_emとprojとtime_embedという謎コンポネントがありますが、実際にコードを見てみたら以下のように使われています。
def forward(self, x, timesteps, y=None):
emb = self.time_embed(timestep_embedding(timesteps, self.dim_t))
if self.is_y_cond and y is not None:
if self.num_classes > 0:
y = y.squeeze()
else:
y = y.resize(y.size(0), 1).float()
emb += F.silu(self.label_emb(y))
x = self.proj(x) + emb
return self.mlp(x)
全体的な処理はただの特徴量だけではなく、データの正解ラベルも一緒にdiffusionモデルに利用されます。こちらは以下の論文により、正解ラベルも一緒にdiffusionプロセスを入れることで、特徴量と正解ラベルが同じnoise加えて、特徴量と正解ラベルの関連性のConsistencyが改善できます。
https://arxiv.org/pdf/2102.09672.pdf
Gaussian Diffusion Model
Gaussian Diffusionは「数字」の特徴量に適用され、オリジナルデータに、徐々にgaussianノイスが加えて(Diffusion Process)、そして、noiseが付いた状態から、徐々にnoiseを除外し(Reverse Process)元の特徴量に復元されます。
こちらでは、Loss関数は基本的に、Diffusion Processで加えたnoiseとReverse processで除外したnoiseの全stepのMSE(Mean Square )
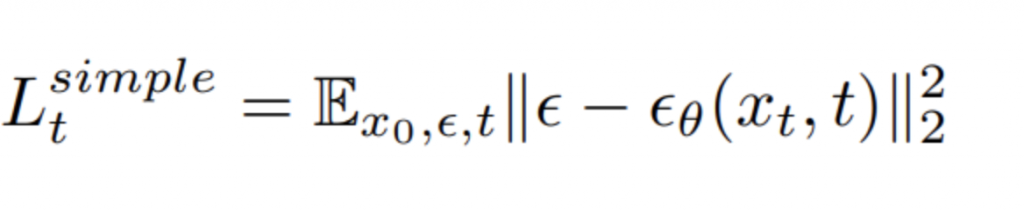
Multinomial Diffusion Model
カテゴリカルデータは基本的に連続数字ではないため、Gaussian Noiseが適用できずに、Gaussian Diffusionモデルが利用できません。その代わりにMultinomial(カテゴリ) Diffusionは使われています。具体的に、
- Diffusion Step:
- Uniformの分布、noise vectorをsamplingし、そのsamplingしたnoise vectorをsoftmax関数に入力し、新しいカテゴリカルデータを取得する
- Reverse Step
- MLPモデルで、noise vectorを予測し、徐々に元のカテゴリが復元して行く。
- Lossの計算
- Lossの計算は基本的に、各t stepのReverseとDiffusionのKullback Leibnerの誤差の合計になります。
具体的なイメージ以下の図になります。

引用:https://arxiv.org/pdf/2209.15421.pdf
学習プロセス
学習プロセス自体は基本的に画像系のDiffusionモデルと同じで、Forward(Diffusion) ProcessとReverse Processで行います。
Forward Process:
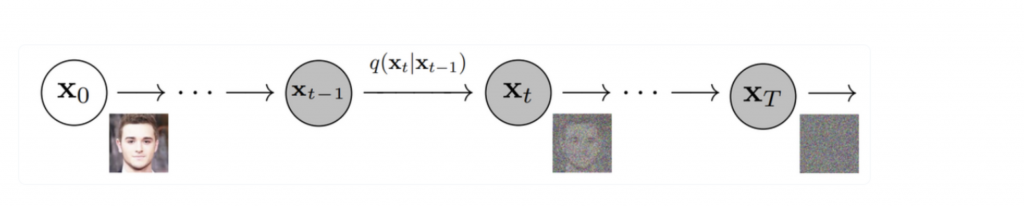
引用:https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
Reverse Process:

引用:https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
Loss関数は基本的に「数字」特徴量のGaussion DiffusionのLossと「カテゴリカル」特徴量のMultinomial Diffusion Lossになります。
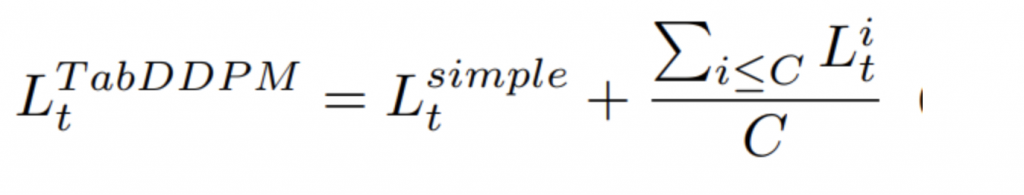
TabDDPMの評価
もとの論文ではTabDDPM優秀な結果得られたと書かれています。特に注目すべきところは以下の観点です。
- Machine Learning Efficiency
- こちらは具体的に生成データのみを利用し、分類・回帰モデルの学習を行い、そして、元データのテストセットで評価行う精度ということです。
- 生成(疑似)データで学習したモデルは実際のデータで精度が良ければ、生成したデータとして優秀で、生成モデル自体も優秀ということです。
- こちらの観点では、他の生成モデル(GAN系、VAE系)に比べて、TabDDPMが精度良いです。
- 生成データと元データの距離
- こちらは生成データと元のデータはどれぐらい距離が離れているかという指標です。
- もちろんできるだけ元のデータと距離が近くなるようにのはゴールですが、元データを完全に同じ(つまり距離0)ができるだけ減らす。同じ程度のML efficiencyスコアーを持っているデータ生成手法(SMOTE)を比較し、SMOTEで生成したデータのほうが元データと同じ(距離0)が多く、TabDDPMのほうが良いということです。
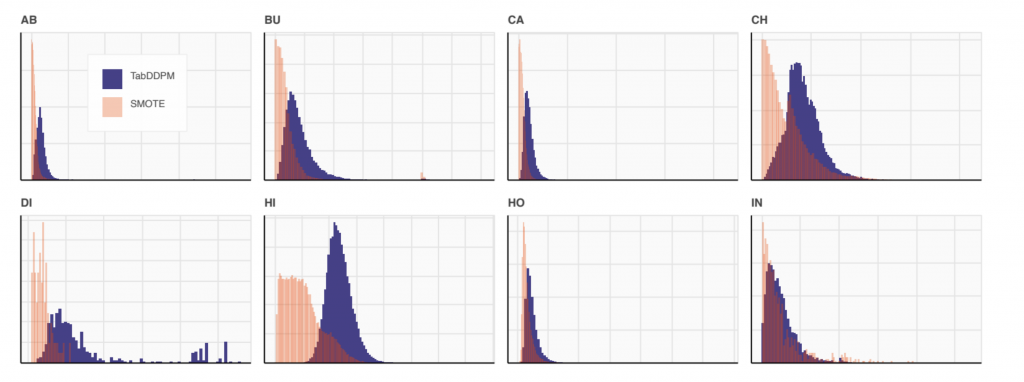
- 引用:https://arxiv.org/pdf/2209.15421.pdf
まとめ
今回は表形式に特化したDiffusionモデルを簡単に紹介しました。表形式データは様々ビジネスでは多く、利用するチャンス出てくる可能性があるかと思います。TabDDPMは生成したデータがそれなりよく、普通の分類モデルなどと組み合わせて以下の問題の解決に利用できるではないかと思います。
- Coldstart時問題
- データ偏り問題
- 秘密性のデータ(個人情報など)の共有
グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD