2024.07.04
ChatGPTにトレーディング戦略を実装させてみる Part2
はじめに
前回の記事ではChatGPTに株のLong/Short戦略を実装させてみるというトピックを取り上げました。
株のLong/Shortというと本来であれば決算データなどのファンダメンタルズに基づいてスコアを算出し、もっとも好ましい銘柄をLong・もっとも好ましくない銘柄をShortするという手法が一般的ですが、簡単に実験できるということでmomentumベースでスコアリングする方法を前回の記事ではご紹介しました。
しかしながらmomentumベースでのLong/Shortではnet positionが中立だとパフォーマンスとしては微妙なので、少しLong側にバイアスをかけるとそこそこのパフォーマンスになるというのが、前回の検証で判明したことでした。
この記事では前回の手法をさらに発展させて、スコアに基づいてLong/Shortのポジションをとるときに、セクターのリスクに対して中立なポジションをとれるように、調整を行う方法をChatGPTに実装させてみることにします。
概要
それでは早速ChatGPTにやり方を聞いてみると、以下のような回答が返ってきました。
株の魅力度スコアに基づくロング/ショート戦略でセクターリスクをヘッジするためには、いくつかの重要なステップがあります。
セクターリスクをヘッジする手順:
- セクターのエクスポージャーを計算する:
- セクターを識別: 各株式をそれぞれのセクターに分類します。
- エクスポージャーの計算: ロングおよびショートポジションの株式のウェイトに基づいて、ポートフォリオの各セクターへのエクスポージャーを計算します。
- セクターのエクスポージャーを中立化する:
- ポジションを調整: 各セクターの正味のエクスポージャーが中立になるように、ロングおよびショートポジションのウェイトを調整します。これは、各セクターでロングポジションの合計額がショートポジションの合計額にほぼ等しいことを意味します。
- 魅力度スコア: 魅力度スコアを使用して、各セクター内のロングおよびショートにする株式を選択します。
- リバランス:
- 定期的なモニタリング: ポートフォリオを定期的に監視して、セクターの中立性が維持されていることを確認します。
- 動的調整: 株価や魅力度スコアの変化に応じてポートフォリオを定期的にリバランスします。
例:
テクノロジーセクターに株式A、B、C、ヘルスケアセクターに株式D、E、Fがあるポートフォリオを持っているとします。魅力度スコアに基づいてポジションを取ると同時にセクターリスクをヘッジしたい場合:
- エクスポージャーを計算:
- ロングポジション: A, D
- ショートポジション: B, E
- ポジションを調整:
- テクノロジーセクターでロングポジションの合計額がショートポジションの合計額と一致するようにします。
- 同様に、ヘルスケアセクターでロングポジションの合計額がショートポジションの合計額と一致するようにします。
- リバランス:
- セクターの中立性を維持するために、定期的にポジションをリバランスします。
実際の考慮事項:
- 取引コスト: ポジションを調整する際に取引コストに注意します。
- 流動性: ロングおよびショートする株式が十分な流動性を持っていることを確認します。
- 分散投資: セクター内での分散投資を維持して、個別リスクを軽減します。
ツールと技術:
- 最適化ソフトウェア: ポートフォリオの最適化ソフトウェアを使用してセクターエクスポージャーを計算および調整します。
- リスク管理ツール: リスク管理ツールを使用してセクターエクスポージャーやその他のリスクを監視します。
これらのステップに従うことで、株の魅力度スコアを活用しながら、ロング/ショート戦略において効果的にセクターリスクをヘッジすることができます。
実装
上記の問題をcvxoptというソルバを用いて解くコードを出力するようにChatGPTに指示してみます。
最初に帰ってくる回答では問題の定式化について言及しています。
問題の定式化:
- 目標: 魅力度スコアの加重和を最大化する。
- 制約:
- ロングポジションのウェイトの合計がショートポジションのウェイトの合計と等しい(セクター中立性)。
- 予算制約(例えば、総投資額が総ショート額と等しい)。
- 任意: ウェイト制約(例えば、ポジションがポートフォリオの一定割合を超えない)。
それでは実装のコード例を見てみましょう。
import numpy as np
from cvxopt import matrix, solvers
# サンプルデータ
stocks = ['A', 'B', 'C', 'D', 'E']
scores = np.array([0.5, 0.2, 0.4, 0.1, 0.3])
sectors = np.array(['tech', 'tech', 'health', 'health', 'finance'])
# セクター中立性制約
sector_neutrality = {'tech': 0, 'health': 0, 'finance': 0}
# 株数
n = len(stocks)
# 目標: 魅力度スコアを最大化する
P = matrix(np.eye(n))
q = matrix(-scores)
# 等式制約: セクター中立性と予算制約
A_list = []
b_list = []
# セクター中立性制約
for sector in sector_neutrality:
sector_mask = (sectors == sector).astype(float)
A_list.append(sector_mask)
b_list.append(sector_neutrality[sector])
# 予算制約: ウェイトの合計 = 0 (ロング合計 = ショート合計)
A_list.append(np.ones(n))
b_list.append(0)
A = matrix(np.vstack(A_list).T)
b = matrix(b_list)
# 不等式制約: ウェイト制限(任意, 例えば -1 <= weight <= 1)
G = matrix(np.vstack([-np.eye(n), np.eye(n)]))
h = matrix(np.hstack([np.ones(n), np.ones(n)]))
# 二次計画法問題を解決する
solution = solvers.qp(P, q, G, h, A, b)
# 解を抽出する
weights = np.array(solution['x']).flatten()
print("最適なウェイト:", weights)
だいたい合っていそうなコードを回答してくれます。
実際に上記のコードを動かすために直す必要があるポイントは以下の通りです。
- セクター中立制約とネットポジションゼロ制約を合わせるとランク落ちになってしまうので、ネットポジションゼロ制約を取り除く
- 等式制約が転置されてしまっているので、元に戻す
ポジション制約の微調整
このままだと単一銘柄で大きなポジションをとってしまう解が出力されてしまうので、1銘柄の最大のポジションサイズは1/銘柄数の範囲に収めてもらうように頼んでみます。
すると以下のようなコードを出力してくれます。
import numpy as np
from cvxopt import matrix, solvers
# Example data
stocks = ['A', 'B', 'C', 'D', 'E']
scores = np.array([0.5, 0.2, 0.4, 0.1, 0.3])
sectors = np.array(['tech', 'tech', 'health', 'health', 'finance'])
# Sector neutrality constraint (sum of longs equals sum of shorts within each sector)
sector_neutrality = {'tech': 0, 'health': 0, 'finance': 0}
# Number of stocks
n = len(stocks)
# Maximum individual stock exposure
max_exposure = 1 / n
# Objective: maximize desirability scores
P = matrix(np.eye(n))
q = matrix(-scores)
# Equality constraints: sector neutrality and budget constraint
A_list = []
b_list = []
# Sector neutrality constraints
for sector in sector_neutrality:
sector_mask = (sectors == sector).astype(float)
A_list.append(sector_mask)
b_list.append(sector_neutrality[sector])
# Budget constraint: sum of weights = 0 (total long = total short)
A_list.append(np.ones(n))
b_list.append(0)
A = matrix(np.vstack(A_list).T)
b = matrix(b_list)
# Inequality constraints: weight limits (-max_exposure <= weight <= max_exposure)
G = matrix(np.vstack([-np.eye(n), np.eye(n)]))
h = matrix(np.hstack([np.ones(n) * max_exposure, np.ones(n) * max_exposure]))
# Solve the quadratic programming problem
solution = solvers.qp(P, q, G, h, A, b)
# Extract the solution
weights = np.array(solution['x']).flatten()
print("Optimal weights:", weights)
これでとりあえず試せそうな実装になったので、上記の修正ポイントだけ反映して以下のような関数を作成します。
前回の検証でネットポジションを少しLongに偏らせた方がよいというポイントを反映して、sector_neutralityも0制約ではなく、少しプラスになるように調整します。
def sector_long_short(scores, cols):
sectors = df_sector.reindex(cols).values
sector_neutrality = {s: 0.25 / pd.Series(sectors).drop_duplicates().pipe(len) for s in pd.Series(sectors).drop_duplicates()}
n = len(scores)
# Maximum individual stock exposure
max_exposure = 1 / n
# Objective: maximize desirability scores
P = matrix(np.eye(n))
q = matrix(-scores)
# Equality constraints: sector neutrality and budget constraint
A_list = []
b_list = []
# Sector neutrality constraints
for sector in sector_neutrality:
sector_mask = (sectors == sector).astype(float)
A_list.append(sector_mask)
b_list.append(sector_neutrality[sector])
A = matrix(np.vstack(A_list))
b = matrix(b_list)
# Inequality constraints: weight limits (-max_exposure <= weight <= max_exposure)
G = matrix(np.vstack([-np.eye(n), np.eye(n)]))
h = matrix(np.hstack([np.ones(n) * max_exposure, np.ones(n) * max_exposure]))
# Solve the quadratic programming problem
solution = solvers.qp(P, q, G, h, A, b)
# Extract the solution
weights = np.array(solution['x']).flatten()
return weights
検証
それではバックテストで上記のストラテジのパフォーマンスを検証してみましょう。
ストラテジの特徴をまとめると以下の通りです。
- 12ヶ月momentumに基づいてLong/Shortのスコアを計算
- ネットポジションは少しLongに偏りを入れる
- 特定のセクターにポジションが偏らないようにセクター中立のような制約を入れる
必要なデータを読み込んでバックテストを回すための周辺コードを以下に示します。
検証期間は2001/01~2017/11とし、対象セクターは比較的成長の大きいInformation Technology, Health Careの2つのセクターとします。
import pandas as pd
import numpy as np
from cvxopt import matrix, solvers
df_stock = pd.read_csv("./stock_sp500_20220623.csv")
df_const = pd.read_csv("./constituents_csv.csv")
df_sector = df_const.assign(Symbol=lambda x: x["Symbol"].str.lower())\
.groupby(["Symbol"])["Sector"].first()
df_sector = df_sector.loc[lambda x: x.isin(["Information Technology", "Health Care"])]
returns_data = df_stock.assign(Date=lambda x: x["Date"].pipe(pd.to_datetime)).set_index(["Date"])\
.resample("1MS").last().pct_change()
returns_data = returns_data.loc[:, lambda x: x.columns.isin(df_sector.index)]
# ポートフォリオのリターンを格納するリスト
portfolio_returns = []
# 各月のポートフォリオのリターンを計算
for i in range(len(returns_data)-1):
if i < 11: # 最初の11ヶ月は過去12ヶ月のデータが揃わないのでスキップ
continue
# 過去12ヶ月のデータを取得
past_12_months_returns = returns_data.iloc[i-11:i+1]
# 各銘柄の過去12ヶ月のリターンの平均を計算し、モーメンタムとする
momentum = past_12_months_returns.mean()
# モーメンタムが大きい銘柄をロングポジション(+1)、小さい銘柄をショートポジション(-1)とする
weight = sector_long_short__(momentum.dropna(), momentum.dropna().index)
# ポートフォリオのリターンを計算し、リストに追加
portfolio_return = returns_data.iloc[i+1].loc[momentum.dropna().index].dot(weight)
portfolio_returns.append(portfolio_return)
# 結果をDataFrameに変換して表示
result_df = pd.DataFrame({
'Date': returns_data.index[12:], # 開始日は最初の11ヶ月をスキップしているのでそれに対応
'Portfolio_Return': portfolio_returns
})
print(result_df)
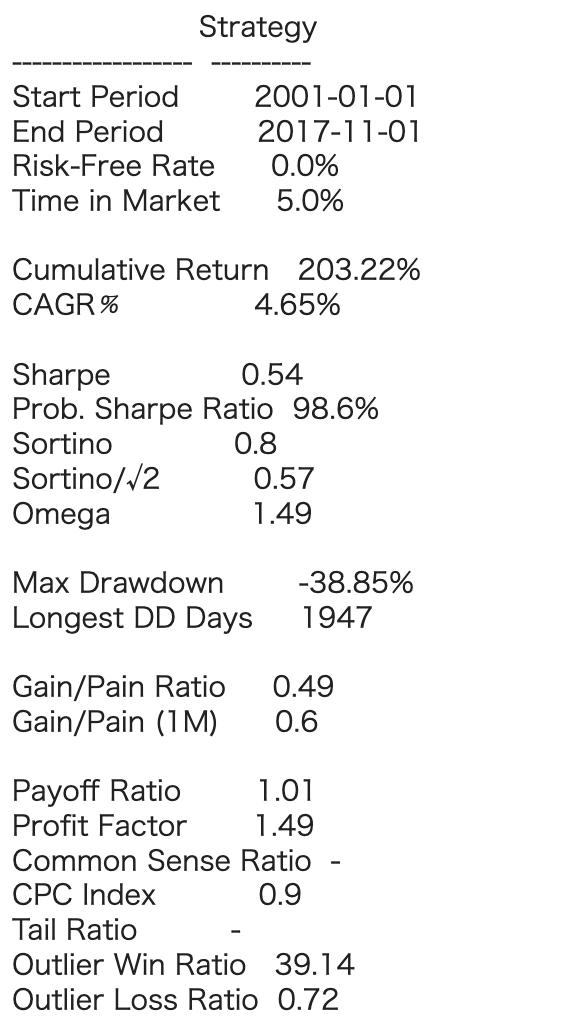
Net Longのポジションが小さいので、2.5倍のレバレッジをかけた結果を示します。
まずまずのパフォーマンスですが今回の対象期間/セクターの場合は普通にBuy&Holdしたほうがよい結果となっています。
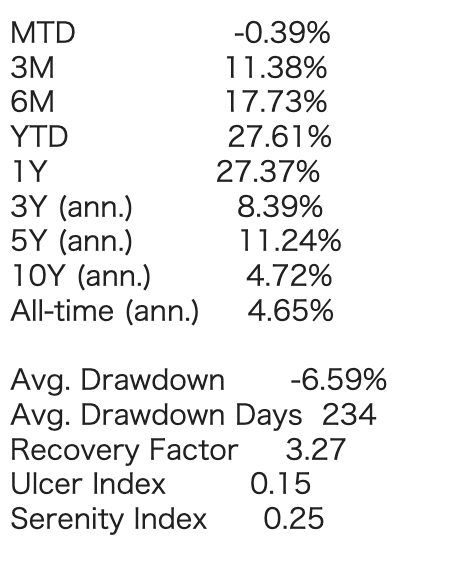
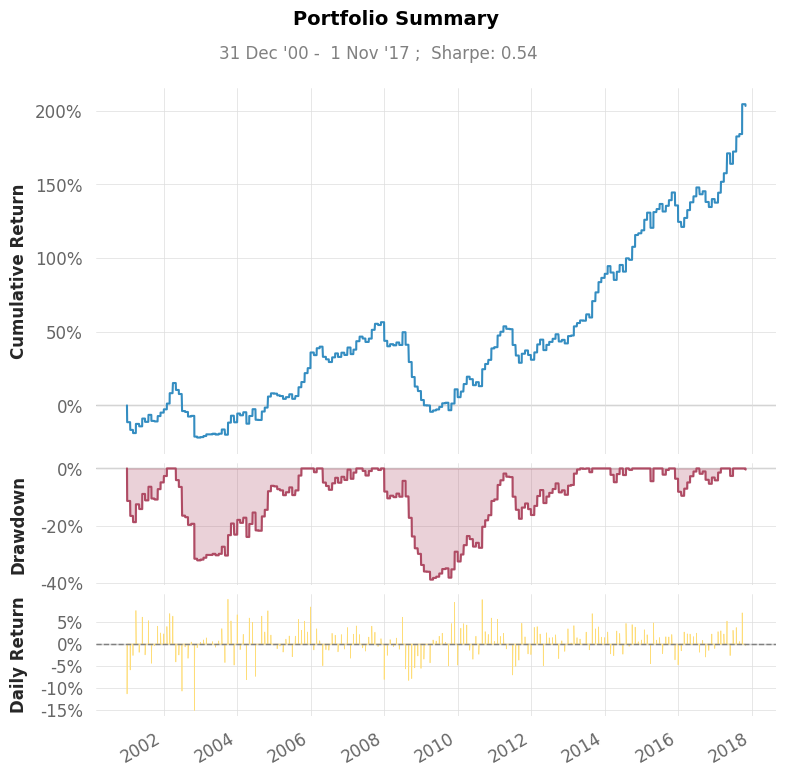
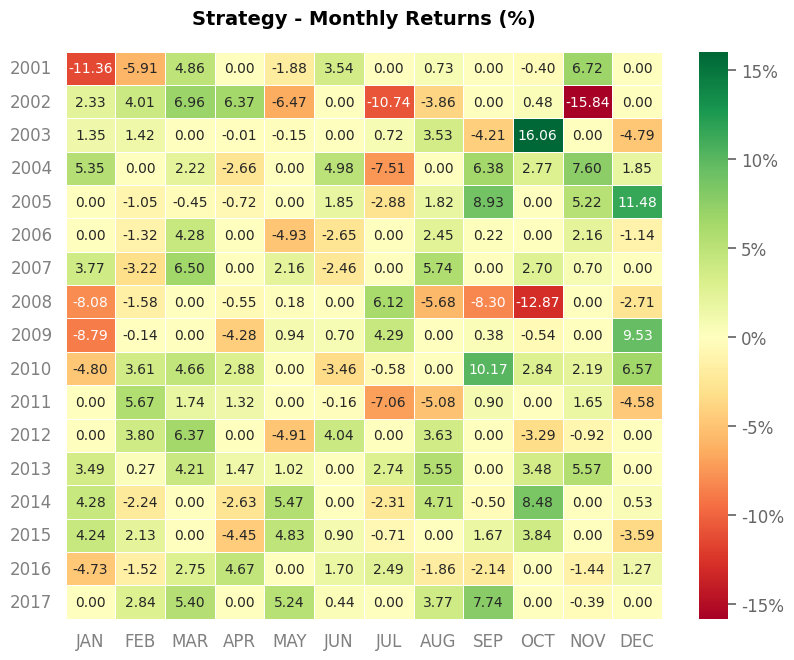
まとめ
前回に続いて株のLong/Short戦略を改善する方法について、ChatGPTに聞きながら実装してみました。
大雑把な質問でベースの回答を得た上で、少し微調整してもらうという流れでそれっぽい実装が用意できることがわかります。
一方で実用レベルのパフォーマンスを出すにはさらなる工夫が必要でしょう。
最後に
グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD