カモにならないアルゴリズム取引：意思決定編

こんにちは。グループ研究開発本部 AI研究開発室のK.S.（女性、外国人）です。

2022Q1はアルゴリズム取引の取引コストと戦略入門を紹介し、2022Q2は取引コストを抑えるための意思決定を深く掘り下げて行こうと思います。

1. 取引コストモデル（Transaction Cost Models）

前回のブログでも紹介しましたが、あらゆる種類の取引の根本的な目標は、取引に隠れたコストを削減することです。したがって、アルゴリズムは、取引コストの影響を考慮し、取引期間全体のマーケットインパクト「自分の取引（売買）で、価格を不利にすることで発生するコスト」とタイミングリスク「売買案件を策定から市場へ発注するまでの間に価格が変動することによって発生するコスト」との間のトレードオフのバランスをとる必要があります。さらに、必要に応じて利用可能な流動性と価格を活用するために、規定された実装ルールが動的プロセスを介してリアルタイムで継続的に更新される場合に最も有益です。今回はマーケットインパクトとタイミングリスクを中心に話し、価格の増価（price appreciation) 「drift, momentumといった一定期間にわたる価格の増加）も少し補足したいです。

それでは、取引コストモデルに必要な用語と数式を見ながら、説明します。

1.1. マーケットインパクト(Market Impact)

マーケットインパクトは取引、又は注文によって引き起こされる価格の変動です。これは注文の情報漏洩と、投資家の流動性と即時性のニーズによる一時的なコストにより構成されます。コスト配分プロセスに基づいて提案されたモデルはI-Starモデルです。このモデルは単一の商品およびポートフォリオレベルでコスト見積もりを処理できるように装備され、さまざまな価格ベンチマークに簡単に適用できます。式は下記になります。

I-Starモデル

$$ I^{*} = a_{1}\cdot \left ( \frac{X}{ADV} \right )^{a2} \cdot \sigma ^{a3}\cdot X\cdot P_{0} $$
\( I^{*} \) は 瞬時インパクトコスト(instantaneous impact cost)、\(X\)は注文の数量、ADV（average daily trading volume）は1日の平均取引数量、\(\sigma\)（annualized volatility）は年間ボラティリティ、\(P_{0}\)は現在の価格、\(a_{1},a_{2},a_{3}\)はモデルパラメーターです。

マーケットインパクトコスト

マーケットインパクトコストは一時的(temporary) と永久(permanent)インパクトで分けられます。取引直前に一時的にインパクトを与えて、しばらく時間が経つと、インパクトが抑えられてきますが、全部は抑えきれなくて、残り部分は永久(permanent)インパクトになります。下記のような式で表せます。

$$ MI_{\$ }(x_{k})=\sum_{j=1}^{n}\frac{b_{1}I^{*}x_{j}^{2}}{X(x_{j}+0.5v_{j})}+(1-b_{1})\cdot I^{*} $$
左の項は一時的(temporary) インパクトで、右の項は永久(permanent)インパクトです。\( x_{j}\)はj期間における数量、\( v_{j}\)はj期間における期待数量、\( b_{1}\)は一時的なマーケットインパクトの割合で、\( 0\leqslant b_{1}\leqslant 1\)です。

1.2. タイミングリスク（Timing Risk）

取引戦略のタイミングリスクは予想されるマーケットインパクトを取り巻く不確実性（uncertainty）です。これは、価格の変動性、1日の取引数量の不確実性、および日中の取引数量パターンの不確実性で構成されます。簡単にするために、タイミングリスクの価格ボラティリティ要素のみを考慮します。

$$ \Re(x_{k})=P_{0}\sqrt{\sum_{j=1}^{n}r_{j}^{2}\cdot t\sigma _{2}/n} $$
\( t\sigma _{2}\)はannualized variance scaled to the length of the trading horizon、\( t\sigma _{2}/n\)は annualized variance scaled to the trading interval、\( r_{j}\)はnumber of unexecuted shares in period j です。

1.3. 他の関連式の参考

価格の増価などの関連式も載せておきますので、参考になればと思います。

Price Appreciation Cost

$$ P{A}’_{dollar/Share}(\alpha )=\frac{X}{ADV}\cdot \frac{a}{\alpha _{_{t}}}\cdot \mu _{t}$$

Execution Prices

$$ E_{0}\left [ \hat{P}(\alpha ) \right ]=P_{0}+sign(X)\cdot (I_{1}\alpha ^{1/2}+I_2) $$

Future Price

$$ E_0({P_{N}})=P_{0}+sign(X)\cdot I_{2} $$

Expected Cost

$$ E_0\left [ \phi (\alpha ) \right ]=sign(X)\cdot (E_{0}\left \lfloor \hat{P}(\alpha )\right \rfloor-P_{b}) $$

2. 定量的な意思決定フレームワーク（Quantitative Decision-Making Framework）

投資家は、全体的な投資目的と取引目標に基づいて様々なパラメーターを選択します。開始時刻と終了時刻、取引数量制限、価格制限、取引数量の最小割合、終値でなどのパラメーターで、取引前に指定する必要があります。それらを判断するためのフレームワークには三つのステップがあり、①価格ベンチマークの選択（Choose Price Benchmark）、②取引スタイルの選択又はリスク回避（Select Trading Style or Risk Aversion）、③適応戦術の指定（Specify Adaptation Tactic）です。

2.1. 価格ベンチマークの選択（Choose Price Benchmark）

意思決定の最初の一歩は、投資するために、希望ベンチマーク価格 （\(P_{b}\)）を選択する必要があります。例えば、前日の終値、当日の始値、到着時価格、当日の終値、などを選ぶことができます。ベンチマーク価格を利用し、効率的な取引フロンティア（Efficient Trading Frontier, ETF）を構築します。ETLは全ての最適な取引戦略のセットで構成されます。例えば、特定のレベルのタイミングリスクに対して最小のコストで、特定のコストに対して最小のタイミングリスクを持つ戦略です。従って、効率的又は合理的なアルゴリズム戦略はETFに存在します。

主なベンチマーク価格は三つあり、前日の終値（previous close）、到着時価格（arrival price to current price）、当日の終値（day’s close）です。

到着時価格の予想コストは、一時的および永久のマーケットインパクトの両方で構成されます。当日の終値の予測コストは、永久のマーケットインパクトが将来の終値に予測され、追加コストを構成しないため、一時的なマーケットインパクトのみで構成されます。これにより、予想ベンチマークコストの低下を反映して、到着時価格より低くシフトされます。前日の終値は、注文価格の動きに応じて、埋没費用又は貯蓄のいずれかを構成します。その結果、前日の終値が到着時価格より、上回ったことに注意することが重要です。


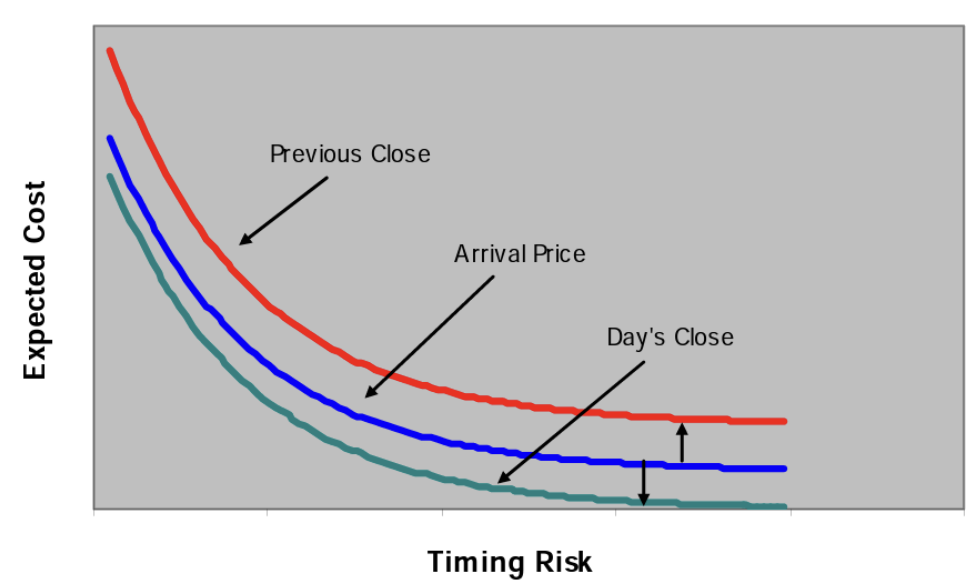
Robert Kissellさんの2005年のAlgorithmic Decision Making Framework論文により転載

それぞれの式の詳細は下記になります。

\(E_0\)は予測コスト（Expected Cost）で、\(Side\)は売りか買いですが、下記の予測コストは買い注文のコストを説明します。

Arrival Price Cost

$$E_0\left [ Arrival Cost \right ]=(\bar{P}-P_{0})\cdot Side$$
そこで、
$$P_{0}=P_{0}$$
$$\bar{P}=P_{0}+(b_{1}\cdot {I}’\cdot \alpha )+(1-b_{1})\cdot {I}’$$
として、
$$E_0\left [ Arrival Cost \right ]=(b_{1}\cdot {I}’\cdot \alpha )+(1-b_{1})\cdot {I}’$$
になります。なので、コストは\({MI}’)\のコストになります。

Previous Close Cost（Historical Cost）

$$E_0\left [ Historical Cost \right ]=(\bar{P}-P_{hist})\cdot Side$$
そこで、
$$P_{hist}=P_{hist}$$
$$\bar{P}=P_{0}+(b_{1}\cdot {I}’\cdot \alpha )+(1-b_{1})\cdot {I}’$$
として、
$$E_0\left [ Historical Cost \right ]=(b_{1}\cdot {I}’\cdot \alpha )+(1-b_{1})\cdot {I}’+(P_{0}-P_{hist}))$$
になります。\(P_{0}-P_{hist})\は遅延コスト（Delay Cost）になり、全体コストはマーケットインパクトと遅延コストになります。

Day’s Close Cost（Future Cost）

$$E_0\left [ Future Cost \right ]=(\bar{P}-E(P_{n}))$$
そこで、
$$E(P_{n})=P_{0}+(1-b_{1})\cdot {I}’$$
$$\bar{P}=P_{0}+(b_{1}\cdot {I}’\cdot \alpha )+(1-b_{1})\cdot {I}’$$
として、
$$E_0\left [ Future Cost \right ]=(b_{1}\cdot {I}’\cdot \alpha )$$
になります。なので、コストは一時的なマーケットインパクト（Temporary Market Impact）です

2.2. 取引スタイルの選択又はリスク回避（Select Trading Style or Risk Aversion）

意思決定の第二段階において、投資家は取引スタイルを指定する必要があります。これは、リスク回避又は緊急性(urgency)のレベルと呼ばれることが多く、マーケットインパクトとタイミングリスクの間の好ましいトレードオフを示します。より積極的な戦略はより高いマーケットインパクトを招き、タイミングリスクを低下させます。より受動的な戦略では、マーケットインパクトが少なくなり、タイミングリスクが高くなります。あるいは、投資家は、公正価格計算又はvalue-at-riskに基づいて、特定のレベルのコストのリスクを最小化し、特定のコストのリスク又は追跡エラーを最小化する戦略を指定することができます。

取引スタイルは主に5つあり、①コスト最小化（minimize cost）、②リスクの制約でコスト最小化（minimize cost with risk constraint）、③コスト制約でリスク最小化（minimize risk with cost constraint）、④コストとリスクのトレードオフのバランス（balance the tradeoff between cost and risk）、⑤価格改善（price improvement）です。今回は「④コストとリスクのトレードオフのバランス」を紹介します

コストとリスクのトレードオフのバランス

最適な取引レート（\(\alpha\)）はコストとリスクのトレードオフをバランスし、下記のような式で表せます。
$$\underset{\alpha }{Min}\ Cost(\alpha ) + \lambda \cdot Risk(\alpha )$$

\( \lambda\)はinvestor specified risk aversion parameterです。\( \lambda=1\)だとリスクとコストは同じくらい考慮し、\( \lambda=2\)だとコストよりリスクを２倍に考え、\( \lambda=1/2\)だとリスクよりコストを２倍に考えることです。

細かく分解すると、下記の式になります。

$${Min}: (b_{1}\cdot{I}’\cdot\alpha +(1-b_{1})\cdot{I}’)+\lambda \cdot (\sigma \cdot\sqrt{\frac{1}{250}\cdot\frac{1}{3}\cdot\frac{X}{ADV}\cdot\alpha^{-1}}\cdot P_{0})$$
最適な取引レートを解くと、パラメータは下記になります。
$$\alpha ^{*}=\left ( \frac{b_{1}\cdot I}{\lambda \cdot \sigma \cdot P_{0}\cdot\sqrt{\frac{1}{250}\cdot\frac{1}{3}\cdot\frac{X}{ADV}}} \right )^{2/3}$$


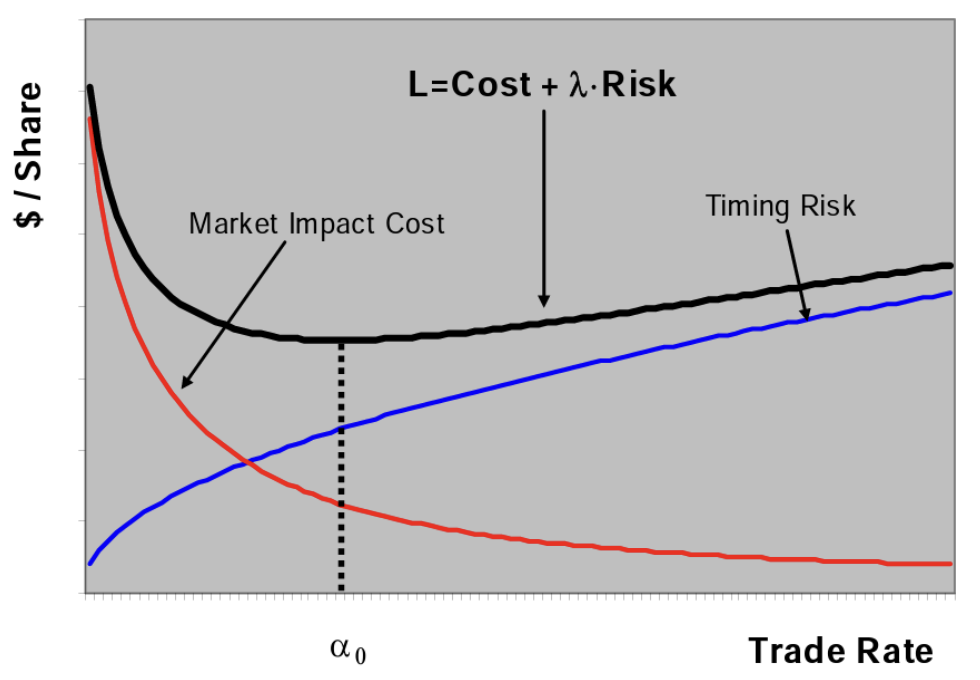
Robert Kissellさんの2005年のAlgorithmic Decision Making Framework論文により転載

2.3. 適応戦術の指定（Specify Adaptation Tactic）

意思決定の第三段階において、投資家が変化する市場の状況にアルゴリズムがどのように適応するかを指定することです。例えば、流動性と出来高のプロファイル、価格の動き、ボラティリティ、S＆Pなどの市場指標（market index）の動き、又は株式の特定のセクターの指標の動きです。適応戦術にはニュース、会社の収益、又は発表を組み込むこともできます。適切な戦術を指定する際には、投資家が決定するコストへの影響、つまり、決定が予測コスト、タイミングリスク、リスクエクスポージャー（value-at-riskなど）、および様々な利益と損失の分布がどのように影響するかを完全に理解することが不可欠です。

ここでは、主な三つの価格ベースのスケーリングアルゴリズムがあり、①Target Cost、②Aggressive in the Money (AIM)、③Passive in the Money (PIM)です。

Target Cost

Target Cost適応戦術(Targeted Cost Adaptation Tactic)は予想コスト「\(E_{t}\left [ \phi (\alpha ) \right ])\」と参照コスト「\(\phi _{ref})\」の差の二乗を最小化します。不必要な市場へのマーケットインパクトコストが発生しないように、有利な価格変動の場合はより積極的（aggressive）になり、不利な価格変動の場合はより受動的（passive）になります。一定の取引レートと比較して、target cost適応戦術は平均してコストが低くなりますが、リスクエクスポージャーが増加します。式は下記になります。

$$\underset{\alpha_{t} }{Min}\ L=\left ( E_{t}\left [ \phi (\alpha ) \right ]-\phi _{ref} \right )^{2}$$

Aggressive in the Money（AIM）

Aggressive in the Money適応戦術(AIM Adaptation Tactic)は実際のコストが参照コストよりも低くなる確率を最大化します。これは、パフォーマンスが参照コストから実際のコストを差し引いた差として測定されるシャープレシオ（Sharpe ratio）を最大化することと同じです。これは、取引の情報比率を最大化することとして定義されます。AIM戦術は有利な価格の場合にはより積極的になり、不利な価格変動の場合にはそれほど積極的ではなくなりますが、継続的な有利な価格と価格リスクの間のトレードオフを管理する方法です。それはTarget Cost適応戦術と同様の動作ですが、さらに価格リスクが組み込まれています。

一定の取引レートと比較すると、AIMは平均してコストは低くなりますが、リスクエクスポージャーは増加します。Target Cost適応戦術と比較すると、AIMのコストはわずかに低く、より良い価格の可能性が高くなりますが、これにはリスクのエクスポージャーが高くなります。数式は下記になります。

$$\underset{\alpha_{t} }{Max}\ L=\frac{\phi _{ref}-E_{t}\left [ \phi (\alpha ) \right ]}{E_{t}\left [ \Re (\alpha ) \right ]}$$
又は
$$\underset{\alpha_{t} }{Min}\ L=\frac{E_{t}\left [ \phi (\alpha ) \right ]-\phi _{ref}}{E_{t}\left [ \Re (\alpha ) \right ]}$$

Passive in the Money（PIM）

Passive in the Money適応戦術(PIM Adaptation Tactic)は潜在的な損失を制限し、利益を共有する機会を提供するという基本的な目標を持つ価格ベースのスケーリング戦術です。例えば、PIM戦術は潜在的な不利な外れ値を管理します。PIMは価格がベンチマーク価格から大きく外れる可能性を減らすために、価格が不利に動く時に、より積極的になります。有利な価格の時期にはより受動的になり、有利な項向が続く場合はより良い価格で参加する機会が与えられます。AIMとは逆の動作をします。

一定の取引レート戦略と比較して、PIMは平均してわずかに高いコストを実現しますが、リスクエクスポージャーが減少し、より良い価格に参加する機会が増加します。数式は下記になります。

$$\underset{\alpha_{t} }{Max}\ L=\frac{E_{t}\left [ \phi (\alpha ) \right ]-\phi _{ref}}{E_{t}\left [ \Re (\alpha ) \right ]}$$

Cost Consequence

戦略が最初に規定された取引レートから逸脱すると、予想されるコスト配分が変更されます。しかし、予想されるコストが減少し、不利な価格への全体的にリスクエクスポージャーが増加し、より有利な価格の可能性が減少するため、フリーランチはありません。不利な価格へのリスクエクスポージャーを減らし、より良い価格の可能性を高めることは可能ですが、これは予想されるコストの増加を犠牲にしてもたらされます。例えば、ターゲットをAIMの両方の戦術は、平均してより良い価格（より低いコスト）に関連つけられていますが、これは「悪い」リスクの増加と「良い」リスクの切り捨てを犠牲にしてもたらされます。PIMは価格の不利な動きの時期により積極的になるため、予定より早く終了する可能性があります。従って、不利な傾向が続く場合、投資家は不利な価格から保護されます。また、アルゴリズムは有利な価格の時に遅くなるため、傾向が続く場合は非常に有利な価格に参加する機会を提供しました。これらの様々な適応戦略の変化率は買い注文について、下記の図に示されます。価格が高くなるにつれて目標が高くなり、AIMがより受動的になり、価格が低くなりにつれてそれらにより積極的になることに注意してください。また、AIMはコストとタイミングのリスクを同時に管理するのに対し、ターゲットはコストのみを管理するため、AIMの適応戦術はターゲットよりも遅い速度で変化します。逆に、PIMはAIMとは正反対の方法で動作します。この場合、価格が上昇するとリスクを切り詰めるためにより積極的になり、好ましい傾向の場合にはより良い価格を利用するためにより受動的になります。


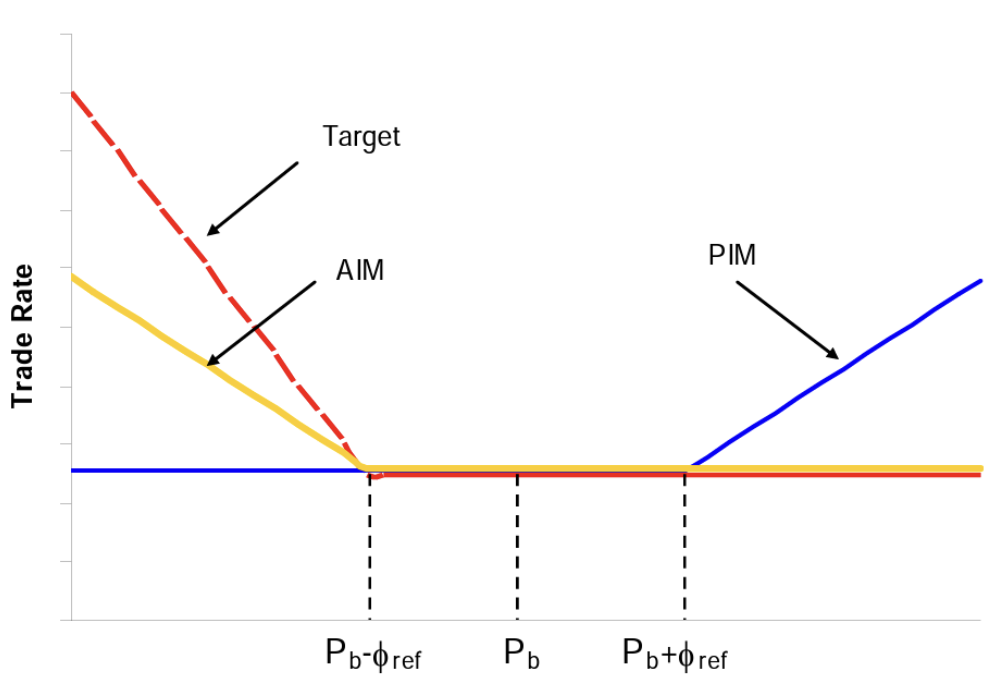
Robert Kissellさんの2005年のAlgorithmic Decision Making Framework論文により転載

3. 実装

いよいよ、実装です。

やりたいことは過去の株価データに基づいて、簡単な取引戦略で意思決定フレームワークを使ってバックテストしてみることです。

3.1. 実装環境とデータ処理

実装環境

環境はGoogle Colaboratoryを利用しました。バックテストはbacktraderというPythonバックテストライブラリを使います。また、可視化のため、backtrader_plottingを使用し、portfolio分析のため、pyfolioを使いました。

データセット

データセットは前回のブログと同じで、yahoo financeのデータを利用しました。下記のように、yahoo finance APIからデータをダウンロードし、自動的にbacktraderシステムに投入できます。これはyahoo financeに情報が入っている銘柄（株、為替、ビットコイン、など）に対応していますので、結構便利です。

3.2. 簡単な意思を試してみた

やってみたいことはバックテストで上記の説明した「価格ベンチマークの選択」を試してみることです。

バックテストした商品はGMOインターネットの株の2010/1/1から2021/12/31です。戦略は前回のブログで紹介したSMA Crossover戦略を適用しましたので、戦略のコストは前のブログに参考してください。また、より実際の取引状況を再現するため、Slippage=0.5%とCommision=0.1%を設定しました。

前回のSMA実装は高速SMAが低速SMAを超えたら、買いシグナルを示し、逆でしたら、売りシグナルを示します。日足でバックテストし、シグナルが超えたら、次の日は終値の価格を取引します。これは少し遅れが発生し、コストとリスクが発生します。今回は、当日の終値で売買し比較してみます。実際は日が終わらないとSMA計算できません。なので、少しチートですが、Arrival Priceを仮定し、価格がわかったタイミングですぐ取引できると前提状況としてテストします。Backtraderでの実装は簡単で、cheat-on-closeの機能を使えば、テストが可能になります。また、実際の取引は様々なマーケット要因がありますが、今回はそれらを考慮しない前提です。実装の例は下記になります。

# set up engine
cerebro = bt.Cerebro()
 
# add strategy
cerebro.addstrategy(SmaCrossOver) # SmaCrossOver, SimpleMeanReversion, SmaCrossUpStopLoss
 
# download data and add to backtest system
data = bt.feeds.PandasData(dataname=yf.download('9449.T', '2010-01-01', '2021-12-31'))
# data = bt.feeds.PandasData(dataname=yf.download('9449.T', '2022-06-27', '2022-07-01', interval="1m"))
# data = bt.feeds.PandasData(dataname=yf.download('AAPL', '2022-06-27', '2022-07-01', interval="1m"))
 
cerebro.adddata(data, name="test")
 
# set cash
cerebro.broker.setcash(1000.0)
 
# set commission
cerebro.broker.setcommission(commission=0.001) # 0.001 => 0.1%
 
# # set coo (cheat-on-open) and coc (cheat-on-close)
# cerebro.broker.set_coo(True)
cerebro.broker.set_coc(True)
 
# set slippage
cerebro.broker.set_slippage_perc(0.005)  # 0.005 => 0.5%
 
# add analyser
cerebro.addanalyzer(bt.analyzers.PyFolio, _name='pyfolio')
 
# print out the starting conditions
print('Starting Portfolio Value: %.2f' % cerebro.broker.getvalue())
 
# run backtest
results = cerebro.run()
 
# analyse portfolio
strat = results[0]
pyfoliozer = strat.analyzers.getbyname('pyfolio')
returns, positions, transactions, gross_lev = pyfoliozer.get_pf_items()
 
# print out the final result
print('Final Portfolio Value: %.2f' % cerebro.broker.getvalue())

 

結果、1000円を投資すると、通常のバックテストの場合、損益=3286.39円を儲かりましたが、Max drawdown=-27.375%、Sharpe ratio=0.61でした。チートする場合、損益=3414.81円を儲かることが可能になったようですが、Max drawdown=-29.488%、Sharpe ratio=0.65でした。全体的に、損益がよくなったが、Max drawdownが低くなった結果でした。

この結果を具体的な例として、上記の理論に合わせて解説してみると、コストとリスクのバランスはまだ改善余地があるのではないかと思います。理想はコストが低くなり、リスクも抑えるようなモデルです。

4. まとめと考察

今回は定量的な意思決定フレームワーク（Quantitative Decision-Making Framework）を紹介しました。主なマーケットインパクトとタイミングリスクを中心に間接的なコストを表現しました。様々な戦略をバックテスクするときに、想定よりコストがかかってしまう可能性があることが伝わればと思います。

参考

• https://www.sciencedirect.com/book/9780128156308/algorithmic-trading-methods/
• https://www.backtrader.com/
• https://jot.pm-research.com/content/1/1/12

最後に

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧からご応募をお願いします。皆さんのご応募をお待ちしています。

一緒に勉強しながら楽しく働きたい方のご応募をお待ちしております。