ブロックチェーンの新たな言語　Simplicityの論文を読む　−Core Simplicity編−

こんにちは。F.S.です。

2017年10月30日にビットコインコア開発者が多数所属するBlockstream社のエンジニアであるRussell O’Connor氏より、ブロックチェーンの新たな言語（ビットコイン・スクリプトに替わるもの）が提案されました。

既存のビットコインスクリプトやEVM, Solidityの改善案として提案された、ループや再帰を用いない静的型付け・コンビネータベースの関数型言語とのこと。チューリング完全でなく、Bit Machineにより空間的・時間的な計算リソースを見積もることができるため、静的解析に適しているようです。
このような特性が有用なスマートコントラクトの構築に十分だとされています。

論文

Simplicity: A New Language for Blockchains
https://blockstream.com/simplicity.pdf

論文公開時のメーリングリストの投稿を見ると、実装についてはまだR&D段階とのことです。
論文ではBit Machineやブロックチェーンへの統合についても触れられてますが、今回は基本概念のCore Simplicityについて内容を見ていきたいと思います。

デザインゴール

Core Simplicityに行く前に、1章に書かれているSimplicityのデザインゴールだけ確認しておきます。

• ノベルプログラムやスマートコントラクトを構築するのに必要なツールを提供する表現力のある言語をつくる
• 必要な計算量の利用可能な上限を提供する静的解析ができる
• 帯域、ストレージ要求を最小限にし、かつ履行時に使われないコードを取り除くことでプライバシーを強化する
• ビットコインの自己充足型トランザクション設計を維持し、プログラムがトランザクション外の情報にアクセスしなくて良い
• 既存の証明支援ソフトウェアを用いてプログラムの推論を容易にする形式意味論を提供する

本言語はプログラマーが直接記述する言語というよりスマートコントラクトを実行するための低レベルの言語として定義されており、他の高級言語からコンパイルされるものと記載されています。

Core Simplicity

Tシャツに収まるほどシンプルだとのこと。

Dr. O’Connor’s t-shirt at #PLAS2017 w/ Simplicity’s complete denotational & operational semantics for provable code: https://t.co/jhPCQU2s3o pic.twitter.com/8vSQwT8RXK

— Christopher Allen (@ChristopherA) 2017年10月31日

BITCOIN MAGAZINEでも紹介されていました。
Introducing a Programming Language so Simple, It “Fits on a T-shirt”
https://bitcoinmagazine.com/articles/introducing-programming-language-so-simple-it-fits-t-shirt/

論文著者のRussel氏はHaskell技術者で形式的証明の検証マシンを開発していたこともあり、論文を理解するには型システム、単純型付きラムダ計算、形式的証明などの知識が必要です。Haskellプログラマであれば馴染みやすいのかもしれません。ちなみに、筆者はこの辺の理論に明るくないため、なんとなく雰囲気はわかりつつもちゃんと説明できるほどの理解が難しく、その点ご了承ください。

理解の助けとしてTAPLと呼ばれるこちらの書籍を参照するのが良さそうです。

• Types and Programming Languages – Benjamin C. Pierce著
  （日本語訳版）型システム入門 −プログラミング言語と型の理論−

ただ、書籍の内容は大学の教科書レベルなのでちゃんと理解するにはそれなりの覚悟と時間が必要ですね。。

それでは、内容を見ていきましょう。

型

Simplicityの型は以下の3つがあります。

• ユニット（Unit）型
  • と表記する。
  • 要素が一つしかない型。
  • Haskellのような関数型プログラミング言語では、Unit型というのは値がないことを表す型で、値をただ一つのみ持つものと定義されているようです。
    これは、C言語などでいうvoidのような役割を持つものらしい。
• 直和（Sum）型
  • A　＋　B　と表記する。
  • A（左）、B（右）のどちらかの型になるタグ付き共用体（tagged union）
    タグ付き共用体とは、タグを付加情報として持ち、常に正しい型でデータを得られるように設計された共用体とのことです。
• 直積（Product）型
  • A　×　B と表記する。
  • 型A、型Bからなる要素のペア。

項

Simplicityの項はゲンツェンのシークエント計算をベースにして、このように表現しています。
（シークエントとは、演繹による証明過程を示すためによく使われる形式表現だそうです）

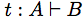
• t はSimplicityの式を表す
• A は入力の型
• B は出力の型
• 記号 ├ はシークエントの表記でターンスタイルと呼ばれるもの。意味的には「生成する」あるいは「証明する」と読まれるようです。

コンビネータ

コンビネータとは、自由変数を含まないラムダ式のことだそうです。
Core Simplicityは9つのコンビネータから構成されており、コンビネータの型付け規則は下図のようになっています。これがTシャツの前面にプリントされているものです。

定義されているコンビネータの内容を見ていきましょう。

• unit：引数は無視し、ユニット型の単一の値を返す（前述のユニット型を参照）
• injl（injection-left）：直和型において、左のタグ付き値を作る
• injr（injection-right）：直和型において、右のタグ付き値を作る
• case：Simplicityの分岐操作。入力の最初のコンポーネントのタグに基づいて、二つの部分表現のうち一つを評価する
• pair：ペア（直積型）を作る
• take：再帰的にペアの第一コンポーネントにアクセスする
• drop：再帰的にペアの第二コンポーネントにアクセスする
• iden（identify）：恒等関数。引数をそのまま返すというもの
• comp（composition）：関数を合成する

iden, compはいかなる型でも使えるコンビネータです。
Simplicityの表現形式は抽象シンタックスツリーで、iden, unitはリーフ、その他7つがノードとなります。各ノードは、ノードが表すコンビネータよって一つか二つの子を持ちます。

表示的意味論（Denotational Semantics）

【参考】 Haskell/Denotational semantics – Wikibooks – ウィキブックス
https://ja.wikibooks.org/wiki/Haskell/Denotational_semantics

Simplicityの項の意味論（セマンティクス）を解説するにあたり、Simplicityのそれぞれ３つの型の値を下記にように表記しています。コロン（：）の右側は対応する型ですね。

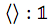• →　ユニット型の値
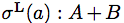• → 直和（Sum）型 A + B の左のタグ付け値（a は型Aの値）
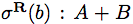• → 直和（Sum）型 A + B の右のタグ付け値（b は型Bの値）
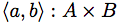• → 直積（Product）型 A × B のペアの値

また、前述のこちらの式を

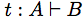
セマンティクスでこのように定義すると

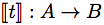
各コンビネータは次の形式で表現されます。これがTシャツの背面にプリントされたものです。なんとなく関数っぽいイメージが湧いてきます。

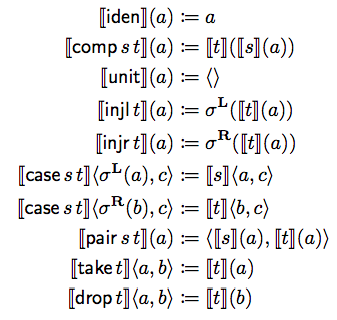
プログラム例

Simplicityにてどのようにしてプログラムが組み立てられるかが、いくつかの例を持って紹介されています。

not関数

よく使われるプログラミング言語ではnot演算子（!）として定義されているものですが、Haskellでは関数で定義されているようです。

まず、1ビットの型を2つのunit型の和として定義します。

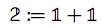
この時、左右それぞれの型において、タグ付けされた値は次のようになります。

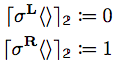
すると、not（ビットの反転）を下記のように組み立てることができます。

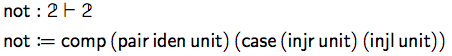
pairの最初のコンポーネント（つまり引数そのもの）を、caseによって

• 左のタグ付け値（=0）の場合は右（intr、つまり1）
• 右のタグ付け値（=1）の場合は左（intl、つまり0）

が評価されるため、ビット反転となります。

半加算器

再帰的にビット型の積をとることで、複数ビットの型を定義することができます。

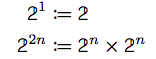
ビッグエンディアン処理系においては、下記のように複数ビット型の値を定義することができます。

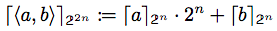
ここで、2つのビット型の半加算器はSimplicityを用いて次のように書けるとのこと。

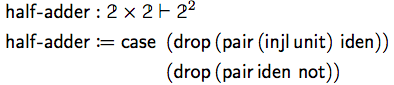
SHA-256

ビットコインのハッシュアルゴリズムとして用いられているSHA-256の計算です。
SHA-256は256ビットのハッシュ値を用いて64バイト（512ビット）のメッセージブロックから256ビットのハッシュ値を求めるものです。つまり、sha-256-blockの型は次のようになります。

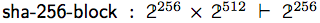
したがって、下記の関数表現となります。

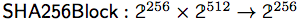
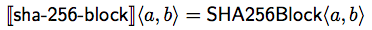
sha-256-blockにおいて、抽象シンタックスツリーのノード数を数えると3,274,442コンビネータになるとのこと。いくつかは重複していて共通化できるため、DAG（有向非巡回グラフ）で表現すると1,130のユニーク型の下位表現となるようです。
証明ツールのCoqを用いると、SimplicityのSHA-256形式証明はOpenSSLのC言語の実装のそれとマッチするのだそうです。

今回はここまで。
新しいもの、ということで興味本位で調べてみたのですが、これだけ理解するのにもなかなか手強かったです。少しはSimplicityの雰囲気が感じられたのかなぁと思います。

それでは、また。

次世代システム研究室では、アプリケーション開発や設計を行うアーキテクト、またはブロックチェーンのエンジニアを募集しています。次世代システム研究室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。