まとめ

• 不均衡のバイナリ変数と連続値の変数の関係を見るとき、相関係数はバイナリが不均衡になると関係性をうまく表現できない場合があり、ROC-AUC値はバイナリの不均衡に対して頑健であるという結果がシミュレーションで示された

• 常にこのような結果となるかは、理論的な説明が必要になってくる。

 

AI研究開発室のM.S.です。

ROC-AUC値とは

ROC-AUC値は、バイナリ分類モデルの性能を評価する指標の一つです。具体的には、モデルの「真陽性率（TPR）」と「偽陽性率（FPR）」の関係を可視化するROC曲線と、その下の面積（AUC）によってモデルの性能を定量的に評価します。

様々な解説記事がありますが、以下の2つの記事がわかりやすかったです。

【評価指標】ROC 曲線と AUC についてわかりやすく解説してみた

AUCをちゃんと説明できないはずがない

上記のブログでも強調されていますが、ROC-AUC値の特長としては、「しきい値に依存せずにモデルを評価することができる」ことが上げられ、しきい値をコントロールすることで容易にhackすることができるrecall等の指標と異なり、よりモデルの普遍的なよさを掴むことに適しています。

このROC-AUC値ですが、「不均衡データに対して頑健性が低い」という記事がネット上では散見されている一方で、 chatGPTでは「不均衡データに対しても有効である」と言われており、この部分を理解するためにシミュレーションを行いました。

問題提起

• ROC-AUC値は不均衡データに対して、過大評価をしてしまうのか。

実験

１.データの不均衡度とROC-AUC値の関係

まずyとy_hatの相関が固定されている状態でデータの不均衡度を変化させて、ROC-AUCへの感度をみてみます。

手順

以下の手順を踏みます。

• データの不均衡度p0を定義して、その比率で[1,0]のバイナリであるyを生成します。例えば、1000このサンプルを生成するとして、p0=0.1であれば、1が100こ, 0が900こ生成されます
• そのyに対して、相関係数がrho(例えば0.2)になるように調整されたy_hatを生成します。
  • y_hat = a * y + ε　でaは相関係数が決められた値になるように調整します。
  • εは平均０分散１の正規分布です。
  • このため、aが「y∈(1,0)の違いをどの程度y_hatに反映させるか」を担っていて、εが「その反映にノイズを与える」ことを担っていることがわかります。
  • この生成方法は理論的に導くことができます。（※1）
• yとy_hatのROC-AUC値を比較します。

import numpy as np
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt
from scipy.stats import norm


# サンプル数
n = 100000

def mk_samples( n, p0, rho=0, a_def=None):

  # y_hatの生成（0と1の割合が1:1000）
  p1 = 1 - p0
  y = np.random.choice([1, 0], size=n, p=[p0, p1])

  # εの生成（標準正規分布）
  epsilon = np.random.normal(0, 1, size=n)

  # 係数aの計算
  var_y = p0 * p1  # Var[y]
  sigma_y = np.sqrt(var_y)  # σ_y

  # 正しいaの計算
  a = rho / (sigma_y * np.sqrt(1 - rho**2))

  print(f"a={a:.2f}")

  # yの計算
  if a_def is not None:
    y_hat = a_def * y + epsilon
  else:
    y_hat = a * y + epsilon

  return y_hat,y

def calculate_auc(y, y_hat):
    # Calculate the AUC (Area Under Curve)
    auc = roc_auc_score(y, y_hat)

    return auc

def show_auc_curve(y, y_hat, ax):
    # FPR, TPR, AUC値の計算
    fpr, tpr, _ = roc_curve(y, y_hat)
    auc = roc_auc_score(y, y_hat)
    
    # ROC曲線の描画
    ax.plot(fpr, tpr, label=f'ROC Curve (AUC = {auc:.2f})', color='blue')
    ax.plot([0, 1], [0, 1], 'k--', label='Random Model (AUC = 0.5)')
    
    # グラフの装飾
    ax.set_title(f'ROC Curve (AUC = {auc:.2f})')
    ax.set_xlabel('False Positive Rate (FPR)')
    ax.set_ylabel('True Positive Rate (TPR)')
    ax.legend(loc='lower right')
    ax.grid(True)

p0_values = [0.5, 0.1, 0.01, 0.001]
rho_values = [0.05, 0.1, 0.2]

fig, axes = plt.subplots(4, 3, figsize=(15, 20))
fig.suptitle('ROC Curve for Different p0 and rho Values', fontsize=16)

# 各p0とrhoでループ
for i, p0 in enumerate(p0_values):
    for j, rho in enumerate(rho_values):
        # サブプロットの選択
        ax = axes[i, j]
        
        # サンプル生成
        y_hat, y = mk_samples(n, p0, rho)
        
        # AUC曲線の表示
        show_auc_curve(y, y_hat, ax)
        
        # 相関係数を計算して表示
        corr = np.corrcoef(y_hat, y)[0, 1]
        ax.text(0.05, 0.9, f'Corr: {corr:.4f}', transform=ax.transAxes)

        # 各サブプロットのタイトルに p0 と rho を表示
        ax.set_title(f'p0: {p0}, rho: {rho}')

# 行ごとにp0ラベルを左端に表示
for i, p0 in enumerate(p0_values):
    # 左側のグラフのy軸にp0のラベルを追加
    axes[i, 0].set_ylabel(f'p0: {p0}', rotation=0, labelpad=40, fontsize=12, va='center')

# 列ごとにrhoラベルを上端に表示
for j, rho in enumerate(rho_values):
    # 上端のグラフのタイトルにrhoのラベルを追加
    axes[0, j].set_title(f'rho: {rho}', fontsize=12)

# レイアウトの調整
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

結果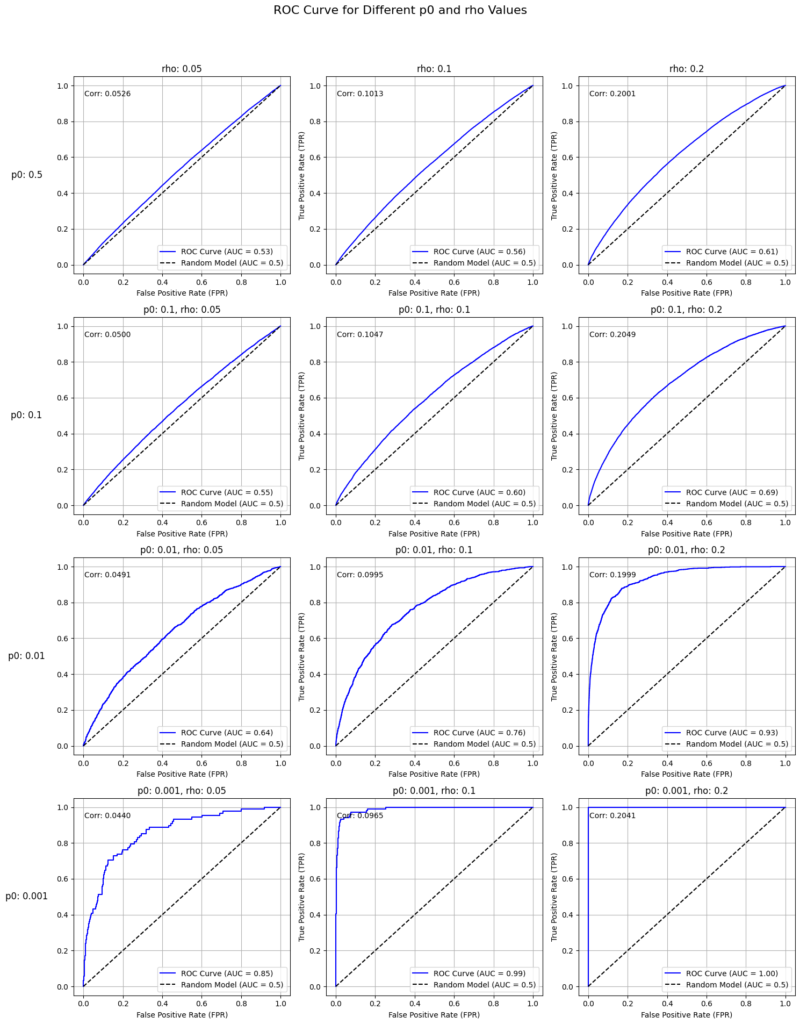

以下の2点がいえます。

• 相関が大きくなる＝右にいくほどAUCが大きくなることがわかります。
• データの不均衡度が大きくなる＝下にいくほどAUCが大きくなることがわかります。

ここから相関係数を固定した状態でデータの不均衡度が大きくなると確かにROC曲線が左上に張り付き、AUC値が大きくなると言えそうです。

 

果たしてそうなのでしょうか？

yやy_hatの値を見てみると、相関を固定するという前提がおかしいことに気づきます。

というのもデータの不均衡度がおおきくなるにつれて、y_hatを発生させる際に用いるaの値が大きくなっていくことがわかります。これは、つまり、「データが不均衡なためみかけのAUCがあがっているのではなく、yの正例と負例でy_hatの値が乖離しているのでAUCが上がっている、逆に相関係数は不均衡データに対して、yとy_hatの関係を過小評価している」といえそうです。（※２）

 

2. データの不均衡度とROC-AUC値の関係の深堀り

相関係数は不均衡データに対して、yとy_hatの関係を過小評価しているという仮説を検証するためaの値を固定する＝y∈(1,0)の違いをどの程度y_hatに反映させるかを固定するという方法で実験してみます。この方法はデータの不均衡度にかかわらず、yが正例 / 負例であることに応じて、y_hatが同じくらい異なる値になる（y_hatの平均値の差が同じくらいになる）ので「正例と負例で性質は異ならないが不均衡度のみ変わる」ことを反映する妥当そうな仮定に見えます。

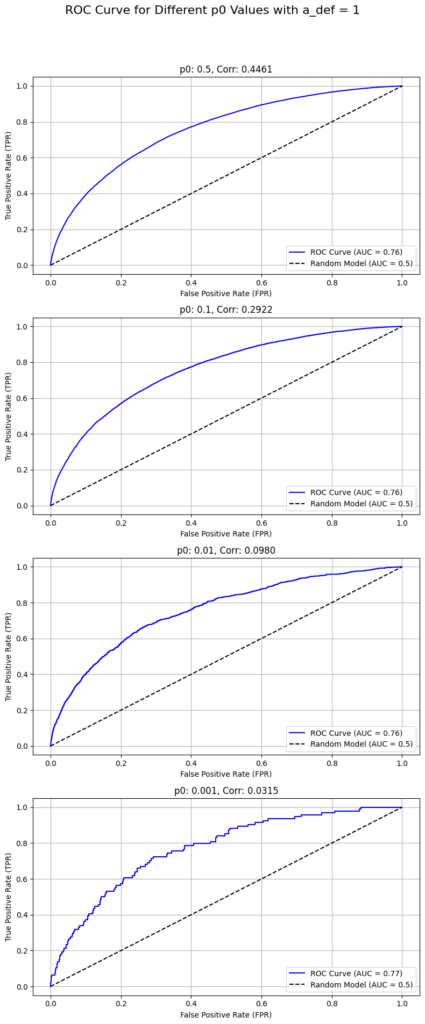
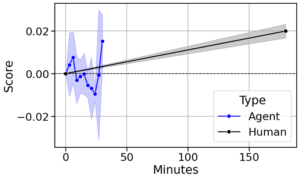
• データの不均衡度が大きくなる＝下にいく、としてもROC-AUC値が変化しない
• データの不均衡度が大きくなる＝下にいくと相関係数は小さくなる（0.44→0.03まで減少）

ここからやはり「（ピアソンの積率）相関係数」が不均衡データに対して過小な数値となる傾向がある指標であることがわかります。相関行列・分散共分散行列が大好きな私にとってはとても驚きが大きい発見です。

3. より妥当な仮定でのデータの不均衡度とROC-AUC値の関係

最後により妥当そうな仮定のもとで、データを発生させて不均衡度とAUC値の関係を考察します。

先ほど「なんとなく妥当そうである、aの値を固定する」という方法を用いましたが、より自然な仮定となるようデータを生成します。特にこれまではy→y_hatの順でデータを生成していましたが、今回はy_hat→yの順でデータを生成します。

具体的には平均値の異なる２つの分布の混合分布からデータy_hatが発生しており、y_hatが大きいほどyが１になりやすいという仮定のもと、２つの分布の各指標が異なるかを見ていきます。これは具体的には、例えばローン審査におけるデフォルト予測モデルを構築する際に大企業（デフォルト率が低い）と中小企業（デフォルト率が高い）でデフォルト率が異なるが、それぞれを対象に審査の機械学習モデルを構築することによってROC-AUC値が異なるのかということに対応します。

コードはchatGPT o1-previewにガリガリ書いてもらって以下になります。パラメタ最適化等必要以上の枝葉のコードがありますが、以下の要件は満たされています。

• コンポーネント0とコンポーネント1という2種類の正規分布で混合正規分布を作成してそこから特徴量 xを生成します。このとき、コンポーネント0とコンポーネント1は平均値が異なる正規分布です。（前述の例ならコンポーネント0が大企業、コンポーネント1が中小企業）。
• このxはy=1のなりやすさを表しており、この値が大きいほどy=1となりやすい（前述の例ならデフォルトしやすい）。
  • • （必然性はないが）xをロジスティック回帰して（0,1）の範囲に変換して、その出力の確率で1となる
    • （必然性はないが）これまでの分析と目線が合うように、相関が0.2くらい、不均衡度が0.1くらいになるようにロジスティック回帰のパラメタを調整している。

import numpy as np
from scipy.special import expit  # シグモイド関数
from scipy.optimize import minimize_scalar

# シードの固定（再現性の確保）
np.random.seed(0)

# サンプル数の設定
n_samples = 100000  # 必要に応じて変更可能

# 1. xの生成
# -------------------------
# コンポーネントの平均値と標準偏差
mu_0 = -1  # クラス0の平均値
mu_1 = 1   # クラス1の平均値
sigma = 1  # 共通の標準偏差

# 混合比率（1:1に固定）
mixing_ratio = [0.5, 0.5]

# コンポーネントの割り当て（クラスラベルの生成）
components = np.random.choice([0, 1], size=n_samples, p=mixing_ratio)

# xの生成（混合正規分布からのサンプリング）
x = np.where(components == 0,
             np.random.normal(mu_0, sigma, n_samples),
             np.random.normal(mu_1, sigma, n_samples))

# 2. β₀の最適化（y=1の割合をp0=0.1に固定）
# -------------------------
# 目標のy=1の割合
p0 = 0.1

# β₁を仮定（後で最適化するための初期値）
beta_1 = 1.0  # 任意の初期値

# y=1の割合を計算する関数
def compute_p0(beta_0, beta_1):
    p = expit(beta_0 + beta_1 * x)
    return np.mean(p)

# β₀を最適化する目的関数
def objective_beta0(beta_0):
    p_mean = compute_p0(beta_0, beta_1)
    return (p_mean - p0) ** 2

# β₀の最適化（y=1の割合がp0に近づくように）
result_beta0 = minimize_scalar(objective_beta0, bounds=(-10, 10), method='bounded')
beta_0_opt = result_beta0.x

print(f'最適化されたβ₀: {beta_0_opt:.4f}')

# 3. β₁の最適化（相関係数が0.2になるように）
# -------------------------
# β₀は最適化された値を使用
beta_0 = beta_0_opt

# 相関係数を計算する目的関数
def compute_correlation_beta1(beta_1, n_trials=10):
    correlations = []
    for _ in range(n_trials):
        p = expit(beta_0 + beta_1 * x)
        y = np.random.binomial(1, p)
        r_pb = np.corrcoef(x, y)[0, 1]
        correlations.append(r_pb)
    return (np.mean(correlations) - 0.2) ** 2

# β₁の最適化（相関係数が0.2に近づくように）
result_beta1 = minimize_scalar(compute_correlation_beta1, bounds=(0, 10), method='bounded', args=(10,))
beta_1_opt = result_beta1.x

print(f'最適化されたβ₁: {beta_1_opt:.4f}')

# 4. 最終的なy_hatの生成と結果の確認
# -------------------------
# 最適化されたβ₀とβ₁を使用
beta_0 = beta_0_opt
beta_1 = beta_1_opt

# 各サンプルにおけるy=1の確率を計算
y_hat = expit(beta_0 + beta_1 * x)

# yの生成（確率に基づく二項分布からのサンプリング）
y = np.random.binomial(1, y_hat)

# 実際のy=1の割合を計算
p0_actual = np.mean(y)
print(f'y=1の割合: {p0_actual:.4f}')

# xとyの相関係数を計算
r_pb = np.corrcoef(y_hat, y)[0, 1]
print(f'相関係数: {r_pb:.4f}')

# 5. 結果の要約表示
# -------------------------
print('\n--- 最終結果 ---')
print(f'最適化されたβ₀: {beta_0:.4f}')
print(f'最適化されたβ₁: {beta_1:.4f}')
print(f'y=1の割合: {p0_actual:.4f}')
print(f'相関係数: {r_pb:.4f}')

# components == 0 のデータにおける y=1 の割合
mean_y_components0 = np.mean(y[components == 0])
mean_y_components1 = np.mean(y[components == 1])

print(f'コンポーネント0の y=1 の割合: {mean_y_components0:.4f}')
print(f'コンポーネント1の y=1 の割合: {mean_y_components1:.4f}')

コンポーネント0の y=1 の割合: 0.0357 
コンポーネント1の y=1 の割合: 0.1048

 

コンポーネントが異なるとy=1を取る確率が変化しています。コンポーネント０のほうがy=1が少ないです。

# components == 0 のデータにおける y_hat と y の相関係数
corr_components0 = np.corrcoef(y_hat[components == 0], y[components == 0])[0, 1]
corr_components1 = np.corrcoef(y_hat[components == 1], y[components == 1])[0, 1]

print(f'コンポーネント0の y_hat と y の相関係数: {corr_components0:.4f}')
print(f'コンポーネント1の y_hat と y の相関係数: {corr_components1:.4f}')

コンポーネント0の y_hat と y の相関係数: 0.1150
コンポーネント1の y_hat と y の相関係数: 0.1904

データが不均衡なコンポーネント0のほうが、相関係数が小さくなっています。

from sklearn.metrics import roc_auc_score

# components == 0 のデータにおける ROC-AUC
y_hat_comp0 = y_hat[components == 0]
y_comp0 = y[components == 0]
roc_auc0 = roc_auc_score(y_comp0, y_hat_comp0)

# components == 1 のデータにおける ROC-AUC
y_hat_comp1 = y_hat[components == 1]
y_comp1 = y[components == 1]
roc_auc1 = roc_auc_score(y_comp1, y_hat_comp1)

print(f'コンポーネント0の ROC-AUC: {roc_auc0:.4f}')
print(f'コンポーネント1の ROC-AUC: {roc_auc1:.4f}')

コンポーネント0の ROC-AUC: 0.6671
コンポーネント1の ROC-AUC: 0.6682

データの不均衡度とROC-AUCの値は関係がありません。

これらの結果から、変わらず「不均衡のバイナリ変数と連続値の変数の関係を見るとき、相関係数はバイナリが不均衡になると関係性をうまく表現できない場合があり、ROC-AUC値はバイナリの不均衡に対して頑健である」

ということがいえそうです。

注意

• 「データの不均衡度が異なる」ということをどう解釈するかによって結果は異なってきます。実はその制約に応じてROC-AUC値は頑健でないことも有り得そうです。（注釈の※2にその可能性について論じています。）
• そのため、常にこのような結果となるかは、理論的な説明が必要になってきます。

最後に

グループ研究開発本部 AI研究開発室では、データサイエンティスト/機械学習エンジニアを募集しています。ビッグデータの解析業務などAI研究開発室にご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。皆さんのご応募をお待ちしています。

注釈

※1

一般にある変数y(平均が0)が与えられたときに相関が一定の値となるような変数y_hatは以下の式をガチャガチャ解いていくことで求めることができます。

まず、y_hatをyの線形モデルで表し（①）、εを平均0, 分散を1と仮定すると、その他の性質から、制約式②、③が導かれます。この②と③を利用して、aについて解くことができるので、線形モデルのパラメータとして代入して、y_hatとなります。

このあたりはじめはノートに書きながら計算していたのですが、検算も踏まえて、chatGPT o1-previewに質問したところ、ズバリ同じロジックでaの値を算出していてとてつもない進歩を感じました。

 

 

※２

相関係数は不均衡データに対して、yとy_hatの関係をうまく表現できないことの(なんちゃって)理論的背景

（1,0）のバイナリ変数と連続する変数との相関係数は点双列相関係数と呼ばれ、以下で定義されます。

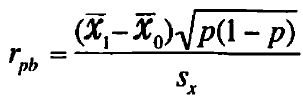
ここで、x_bar₀ ,x_bar₁ はバイナリ変数が0と1のときの平均値、pはバイナリ変数１の割合（＝不均衡度）s_x は連続変数の標準偏差を表します。この値はいわゆる相関係数（＝ピアソンの積率相関係数）と値が一致し、要はピアソンの積率相関係数の式に片方の変数がバイナリであるという仮定を置くと、ガチャガチャ計算することでこの公式を導けるようです。

ここで、不均衡度のみが増していくということは以下のようなことが起きることだと私は考えています。

• 連続変数間のバイナリの条件付き確率（例えば、y=1のときのxの条件つき確率）は、pによらず一定である。→x_bar₁ – x_bar₀ は変化しない。
• 上記が固定されたうえで、pが0に近づいていく。→sqrt(p(1-p))は、sqrt(p)に近づく。s_x はs_x0 （y=0のときのxの標準偏差）に近づいていく。

上記より、p→0になるときに分子がsqrt(p)のスピードで小さくなることと分母がs_x がs_x0 に近づいていくことで、小さくなることの綱引きが起きるといえそうです。

ここから数式的にガチャガチャ式変形をして、確定的なことが言えるかもしれませんが、ここでギブアップです。
ただ、本ケースは分子がsqrt(p)のスピードで小さくなることが分母がs_x がs_x0 に近づいていくことで、小さくなることのスピードより早く、結果として小さな値となったということがいえそうです。

こう考えると、相関係数は不均衡度が増すと小さくなる保証はなく、例えば「y=1とy=0の連続変数の分布間がそもそも大きく離れている」「y=1とy=0の連続変数の分布で、y=1の分布の方が分散が大きい」「異常検知の一次審査を行い異常品の一次的な除去を行う」というような文脈で、データの不均衡度が増す場合は、デーさ発生の仕組みも異なり違った結果となるかもしれません。