Deep LearningをKerasで可視化したい
こんにちは。次世代システム研究室のJK (男)です。
突然ですが書籍の「ゼロから作るDeep Learning」読みましたか？基礎からクリアに説明されていて、個人的にはとても面白かったです。これまでLSTM, 強化学習の記事を書いてきましたが、今回はこの本にならってDeep Learningの基礎の「ちょい深」理解を目指し、Deep Learningの可視化に焦点をあてたいと思います。
ちなみに今回の内容のcodeは、ここに上げておきました。
0. 可視化のモチベーション
最近のDeep Learningのフレームワークは充実していて、簡単に動かせるようになりましたね。でも動かせたけど理解した気がしない、って人も多いのではないでしょうか？その理由の一つが、Deep Learningがブラックボックス化していることだと思います。簡単に動かせることの副作用だと思いますが、インプットデータと教師データを入れれば「学習してくる」ので、中身をあまり理解しなくても形にはなっちゃうんですよね。
「可視化」することによって、実際に中で何がおきているのかを少しでも理解しよう！というのが今回の目的です。今回は人気フレームワークKerasを使って可視化を行います。Kerasは、Tensorflow/Theanoをバックエンドにしたラッパーライブラリで直観的な操作が可能です。既存のフレームワークを使うことで、誰でも手軽に試せるだけでなく、実務レベルでも今回の内容を応用できるんではないかと思ってます。
今回の記事の目次
1. CNN (= 画像認識Deep Learning)のフィルターと中間データの可視化
2. MLP (= 普通?のDeep Learning)のパラメータの可視化と、正則化の可視化
3. MLPのパラメータの可視化と、Dropoutの可視化
4. パラメータの初期分布の違いによる、MLPのパラメータ分布の可視化
1. CNNのフィルターと中間データの可視化
CNNはDeep Learningの花形である画像認識で使われる手法の基礎です。簡単にいえば、インプット画像と「正解ラベル」のデータセットをCNNに学習させることで、別の画像を見せた時にCNNがもっともらしいラベルを答えてくれるという手法です（詳細は書籍やWebでお願いします）。Deep Learningの”Hello world!”ともいえる、MNIST dataの場合で説明すると、
- 手書きの数字の画像と、その数字の「正解ラベル」(0–9のいずれか)のデータセット（MNISTデータ）がある。
- このインプット x 正解のデータをモデルに学習させる。
- 別の手書き数字の画像を見せて（インプットし）、学習したモデルがその数字が0-9のいずれであるかを予想する。
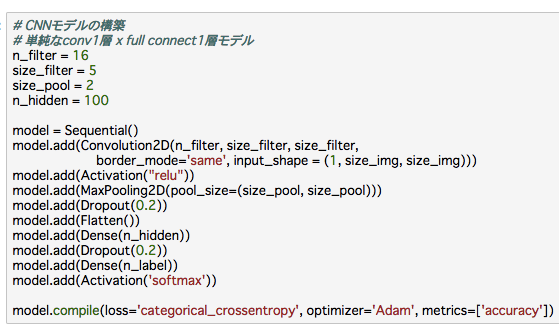
データはMNISTを使います。まずKerasでCNNをモデル化します。今回は簡単に、Convolution層, Max pooling層, フルコネクト層、それぞれ一層ずつです。Kerasで書くと下のようになります。
あとは学習させるだけ。
この学習したモデルで正解率は~99%になりました。すごいですね。ただ不正解のものも~1%はあります。そこで不正解の数字たちを見てみましょう。
青ラベルが実際の数字で、赤ラベルが間違えて予測した数字です。
人が見ても間違えてしまいそうなペアも少しありますが、人なら間違わないペアの方が多いように見えますね。特に0, 6, 8, 9の「円（丸?）」が数字に含まれている数字は、人なら絶対にしないような間違いが多いように感じます。円状の一部が欠けているものを円と判断しなかったり、逆に円でないのに一部の突起のような部分のみで円であると判断したりします。
上記の考察から、CNNのフィルターが「円」を認識する能力が乏しいのでは？と推測できますね。では実際にフィルターを可視化しましょう（やっと「可視化」までたどり着きました。。。）。Kerasだと学習済みの”model”に対して以下のようにすれば、学習済みパラメータ（=重み）を簡単に取得できます。
で、取得したフィルターの画像がこんな感じです（今回のモデルは、5×5サイズのfilterを16種類使いました）。
赤が高く、青が低いので、ざっくりといえば赤部分がフィルターの形状です。フィルターの役割は読んで字のごとく、インプット画像の特徴をフィルターの形状に合わせて抜き出します。こうして16のフィルターを見ると、縦、横、斜め、L字の形状など直線構造はあるものの「円」状のものはないですね。円の形状は、直線状のフィルターを組み合わせて判断していると考えられます。そのため今回のCNNでは（前述したような）「円」そのものでなく、その一部の形を見て判断したような間違いが多いのだと推測されます。
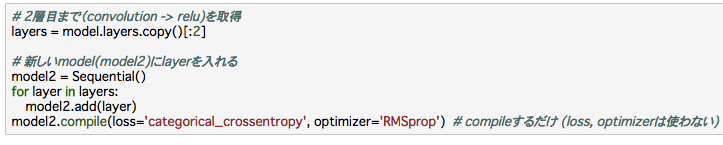
この推測を確認するため、今度は中間イメージ（フィルター直後のデータ）を見てみましょう。Kerasでこれを行うために、少しトリックを使います。下記のように、学習済みmodelから必要なlayer（欲しい中間データが出力される層）まで抜き出し、新しいmodelに使います。このモデル自体はアウトプット層まで構築していないので学習には使えませんが、アウトプットとして欲しい中間データを出力してくれます。
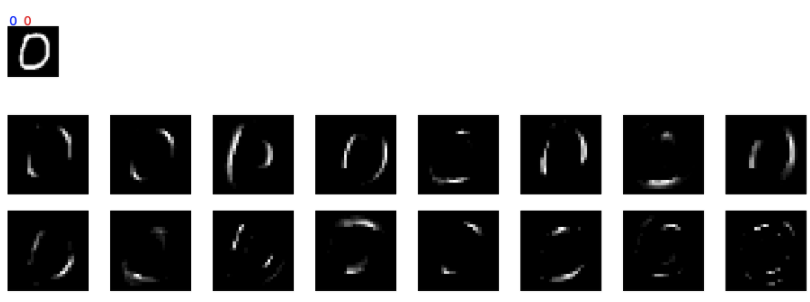
下図が抽出した中間データです。16個のフィルターから、それぞれ出力されるので16枚のイメージになります。一番上の小さいイメージはインプットです。まず正解ラベルが”0″のとき、正しく0と予測した場合です。
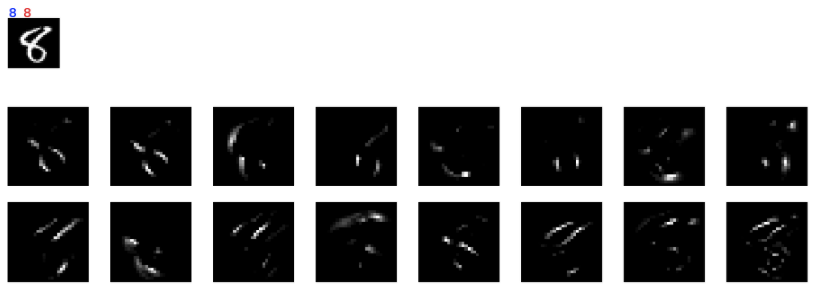
次に間違った場合です。2ケース載せます（0を8と間違えた場合と、2と間違えた場合）。
予想通り、中間イメージは16のfilterの特性に合わせてそれぞれ縦、横、斜めにfilteringされており（フィルターの形状と比較してみてください）、「円」状の中間イメージはないです。縦、横、斜めに断片化されたイメージを組み合わせて「円」と認識していると考えられます。上図の正しく認識されている場合はわかりやすく、人がこの16枚のイメージから判断しても「0」と推測できます。
面白いのは間違っている場合で、1番目の例では明らかに0なのに8と間違えています。おそらく（特に左の）縦線が曲線でなく真っ直ぐ引かれているため、0と認識されなかったと思われます（正解の場合に比べ「斜めfilter」への反応が顕著でない）。だからといって、8には間違えないだろうと思いますが、今回のCNNだと8を正しく推測するのが難しそうです（下図の8の正解データ参照）。人は8を「円が2つ」と認識していると思いますが、このCNNではそのように認識していない。人なら最も注目するであろう、8の中心の結び目(‘X’)部分があまり強調されていない＝そのようなfilterがないんです。これが0と8を間違う原因だと考えられます。
2番目の間違いの例も面白いです。間違いの原因は左の線が途中で切れていることだと推測できますが、人であれば簡単に線を「補完」して0とみなせます。こういう補完に関してはCNNもMax poolingで対応していると思いますが、この数字に関してはMax poolingで対応できる範囲を超えて離れてしまったのでしょう。
（推測ですが）人は直線だけでなく円の大きさなども、イメージに合わせてスケールして認識します。これはCNNでいえばfilter sizeをイメージに合わせて、大きくしたり小さくしたり適宜合わせていることに相当する（はず）。同じように、線が離れすぎていてもイメージごとに柔軟に補完の大きさを変更することもできます。なので、人から見ると上記のようなCNNの間違いを不思議に思います。
今回の単純なCNNではconvolution/Max poolingのfilterの大きさは固定化されています。このような制約の中では、どのようなイメージにでも汎用的に使えるfilterは直線だけだと考えられます（もっとfilter数を多くしたり、filter sizeを大きくすれば円も現れるかもしれない）。実際、円といっても8の円と0の円では大きさが異なるし、書いた人によっても大きさも形状も異なる。固定化されたfilterでは、人のように柔軟に形を検出するのが難しそうだな、というのは直観的にも納得できますね。
と考えると、むしろこんな単純なモデルで99%の正解率がであることが驚異的に感じます。ただ忘れてはいけないのは、インプットされている数字は人によって事前にtrimingされたりリスケールされたりしていることです。つまりCNNが苦手とする柔軟にスケールする能力がなくても（できるだけ）大丈夫なように、イメージのサイズや場所ができるだけ「固定化」されているんですね。というわけで、フィルターされたイメージを見ることで、インプットイメージの前処理の大事さについてまで理解が深まりました（たぶん）。
ここの”viz_cnn.ipynb”の最後のセルに、0-9までの数字について同様の比較を載せておきました。間違えても仕方がないというものから、上記の考察が当てはまる間違い、よくわからない間違いなど色々あります。眺めていると他の法則などもわかるかもしれません。
2. MLPのパラメータの可視化と、正則化の可視化
このセクションではCNNでなくMLP(多層パーセプトロン)のモデルを使い、1層目から2層目への重みを可視化します。最初にチェック用データで、期待通りに重みが可視化できているかをチェック。次にチェックに使用した簡単なデータで、正則化（L1/L2）をした場合、重みがどのように変化するかを見ます。
まずはモデルの構築。Kerasで下のようにサクッと作ります。
inputが10次元で次の隠れ層のunit数30なので、重みの総数は10 x 30 = 300になります。
次にデータを準備します。ここでは“チェック用データ”を作成します。どういうものかと言うと、インプットデータ（特徴量）に解読しやすい正解データの情報を混ぜたものです。正解情報がインプットに入っているので、モデルが適切に学習すればこの正解情報を入れたunitだけに重みが集中し、正解率も100%になると期待できます。ここでは、10次元のインプットのうち、3, 6番目のunitを足すと正解データになるように調整しました。残りのunitの値はランダムに設定したので、正解情報をもたないノイズです。
上記のモデルで、このデータを学習させました。
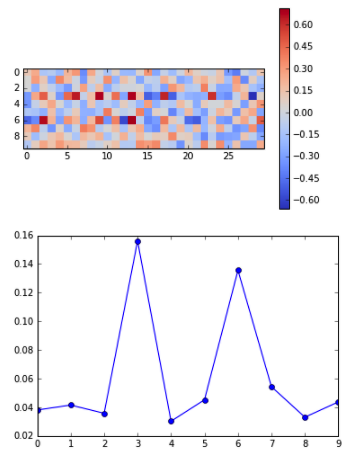
学習した結果、期待通り、正解率は100%になりました。1層->2層目の重みを可視化したものが、上図の2つのパネルです。
- 上パネルは、縦軸がinput (dim_in=10 units), 横軸がそれぞれのunitから次の層（30 units）へのそれぞれの重みの大きさ。重みの絶対値が大きいほど色が濃くなります。
- 下パネルは、行方向（input層）に平均をとったもの（= 各input unitから出ている重みの平均値）。横軸がinput unitの各番号で、縦軸が重みの平均値。
2.1 L1正則化
次にL1正則化をしてみます。L1正則化の項を1層目に入れ、同じデータで学習します。
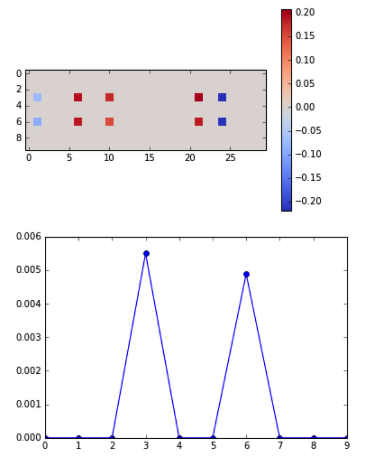
結果は上図のようになります。正解率は変わらず100%でしたが、重みは思った以上に変化がありました。L1正則化は教科書に「余分な次元を削除する」役割であるとよく書かれてますが、実際に可視化してみると、よくわかりますね。まずランダムノイズの項（3, 6番以外）は完全に重みの値が0になっていて実質削除されています。また3, 6番目に関しても、5つのunit以外は全て0で削除されています。今回のチェック用データセットの場合、3, 6番目にそれぞれ1unitずつあれば十分であることを考えると、ここまでunit数が削除されるのも納得でしょうか。もっと上手く設定すると、1unitだけにすることも可能かもしれません。
また重みの絶対値も小さくなっています。「正則化は重みの絶対値を小さくする」という教科書の記述も「たしかにそうやなー」と確認できますね。
2.2 L2正則化
最後にL2正則化をしてみます。L1のかわりにL2正則化の項を1層->2層の重みに入れ、同じデータで学習します。
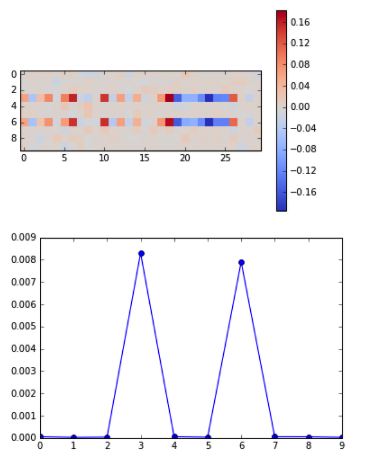
結果は上図のようになります。正解率は変わらず100%ですが、重みを可視化することで、正則化なし、L1正則化、どちらの場合とも異なる重み分布であることがわかります。教科書で「L2正則化は重みの絶対値を小さくする」という記述をよく見ますが、可視化するとその意味がよくわかりますね。ランダムノイズのような（正解データを推測するのに）不要なデータのunit（3, 6番目以外）の重みは、正則化なしの時と較べて非常に小さいです(でもL1のときのように完全削除でもない）。また3, 6番目のunitに関しては、次の層につながる重みが多数あります。5つしかなかったL1のときとは明らかに異なりますね。一方で、一つ一つの重みの大きさでいうと、L1のときより小さいように見えます。少なくとも正則化なしのときと比べると、明らかに絶対値の大きさが小さくなっていることが確認できます。
というわけで、「不要な次元削除」の際はL1を、「重みを小さくしたい」場合はL2という教科書の記述の意味が可視化することでわかりやすくなりました。不要データに関しては、どちらの場合もほぼ0まで落としてくれることがわかりましたが、L1だとやり過ぎ感が漂う（完全に0になるunitが多くなり、ニューラルネットにした恩恵が小さくなる可能性がある）ので、普通に過学習抑制が目的ならL2の方が無難だろうな、ということもこれらの図を見れば納得ですね（少なくとも私はしました）。
紙面の関係でカットしたコードの詳細は、ここの”viz_mlp_check.ipynb”にあります。またここで書いた発展系として、チェック用データでなくMNIST dataを使った場合を”viz_mlp_regularization.ipynb”に書いています。長くなったのでカットしましたが興味があれば見てください。
3. MLPのパラメータの可視化と、Dropoutの可視化
すみません。予定以上に記事が長くなってしまったので、すごーーく簡単に。可視化した重みの分布は正則化の場合とは明らかに異なっており、同じ過学習抑制の手法ですが、アプローチが異なることが可視化からもわかりました。詳しくはここの”viz_mlp_dropout.ipynb”をみてください。
4. パラメータの初期分布の違いによる、MLPのパラメータ分布の可視化
ここも簡単に。重みの広がりは学習によってそこまで劇的に変化するわけではないことがわかりました。ので、極端に初期分布の広がりを制限すると、重みが小さすぎて適切な学習ができません。一方で、ある程度の広がりであれば、あまり学習結果に違いはないように見えます。詳しくはここの”viz_mlp_initalW.ipynb”をみてください。
最後に
最後は駆け足になってしまいましたが、CNNとMLPについて可視化をしました。CNNはMNISTデータを使い、フィルターとフィルター直後のイメージを可視化することで、実際にconvolutionの過程で何がおきているのかの理解を深めました。また不正解データに着目することで、CNNの固定フィルターと人間の柔軟な形状検出の違いもクリアになりました。MLPの場合については、1層目から2層目への重みの可視化を行いました。チェック用データを作って簡易な状況を人為的に作り、正則化なし、L1正則化、L2正則化の場合を調査しました。それぞれの重みの分布を可視化することで、それぞれの特徴の理解を深めました。他にもいくつかのケースを調べましたが、それはここを参照してください。
次世代システム研究室では、ビッグデータ解析プラットホームの設計・開発を行うアーキテクトとデータサイエンティストを募集しています。ご興味を持って頂ける方がいらっしゃいましたら、ぜひ 募集職種一覧 からご応募をお願いします。
私自身、この４月より天文学のポスドクから機械学習という全く新しい世界に来ました。学ぶこともたくさんありますが、データ解析である以上、共通点もたくさんあります。未来を担う技術である機械学習、ディープラーニングに興味のある方は思い切って飛び込んでみるのも一興かと。
皆さんのご応募をお待ちしています。
