2018.01.04
狙え一攫千金!-機械学習でビットコイン投資-
お金が欲しいですか?
私は欲しいです。
お金があれば、長〜い休みをとって夏に北海道は積丹へ行き名産品のうにを食べまくる。ウニ丼の店の常連になった頃、店のご主人に紹介してもらい地元の漁師と友達になり、新鮮なうにが取れた時は送ってくれるようにお願いする。
夏が過ぎたら今度は別の漁の盛んな町へ行き、イカやホタテを食べる。
イカはイカ漁で有名な函館で食べるが、ホタテは猿払で食べる。猿払は北海道の北端に近くに位置する村で、ホタテ以外は何もないが、ホタテしかないだけあって身が大きくてとても美味いものが手に入りやすい。
さらに、コメと言えば最近評価が高いのが北海道米。親の知り合いの農家に直売してもらえばうまいコメが安く手に入る。
おまけに冬は趣味で鹿猟をやってる友人にシカ肉を分けてもらう。
そうやってあちこちの知り合いから最高の食材の独仕入れルートが確保できた頃に、うまい食事をウリにした宿を道内の観光の要所で開く。宿のターゲットは近年ぐっと増えたアジア各国からの外国人観光客。北京語、広東語、英語、その他各国の言葉が話せるスタッフを雇えばお客様も安心して宿泊できる。
そんなライフスタイルを始めるための開業資金と、万が一失敗した時に利息で食べていくための資産が、合計で10億円ぐらいあればなんとかなる。
なるのだけ、そもそも日本のしがないサラリーマンの平均程度の収入では、コツコツ貯金を続けたところで、10億円なんて
いつまで経っても、
未来永劫、
永遠に、
貯まりやしないっ!!!
人生は短い。私は悲しい。
一方、世の中には投資というものがあります。最近話題なのが、皆さんご存知のビットコイン。ニュースによるとここ一年で価値が20倍くらいになったとか。去年ビットコインを1000万円分買って、1年間持っておくだけで2億円になったのです。さらにそれをもう一度繰り返せば、もう40億円。税金を考慮にいれても、十分に目標達成。仮に元手が100万円しかなくても10倍を3回でオッケー。なーんだ、10億円って意外に簡単ですね。
ただし、普通の神経ではそんな大きな元手を使った博打は怖くてできません。ビットコインは確かに価格がロケットのように上がり続けていますが、その反面一日で30%下がるのもわりと平常運転の範囲です。さらに、今のビットコインバブルがいつ弾けるかは誰にもわからないのです。今日1000万円分あったビットコインが明日100万円まで価値がさがったらどうしますか?普通はショックで日常生活に支障が出てしまいます。大金を投資していると、急落を考えるだけで夜寝られません。
それではどうしたらいいのでしょうか?ただ指をくわえてビットコインが値上がりしているのを見ていますか?それはなんだか残念ですね。相場には変化がつきものですが、価格の急落に伴うリスクを自動でコントロールしてくれる仕組みがあれば、投資をつづけながら夜もぐっすり寝られます。投資の自動化をすれば一日中チャートに張り付いている必要もないので、昼間は仕事や家庭の用事に勤しむ事ができ、普通の生活を送る事ができます。さらに、平均的な投資家には真似のできない高度なアルゴリズムを使えば、リスクをコントロールしつつも大幅に利益を上げる事ができるかもしれません。
そういう訳で、今回は機械学習を用いた投資の自動化のためのアルゴリズム、それも普通の手法の先を行く先端的手法の開発に挑戦します。
ボリンジャーバンドとは
それでは投資の自動化の従来的な手法にはどのようなものがあるでしょうか?ビットコインを売買して利益を出すためにはビットコインを安く買って高く売るのが一般的ですね。ならば、ビットコインが安い買い時と、高い売り時を自動で判別して取引してくれる自動化の手法が役に立ちそうです。
そういう時に使えるボリンジャーバンドというものがあります。ボリンジャーバンドは、GMOコインのウェブサイトによると、単純移動平均線を中心に、1標準偏差(1σ)、2標準偏差(2σ)のバンド(線)を上下に表示するものです。
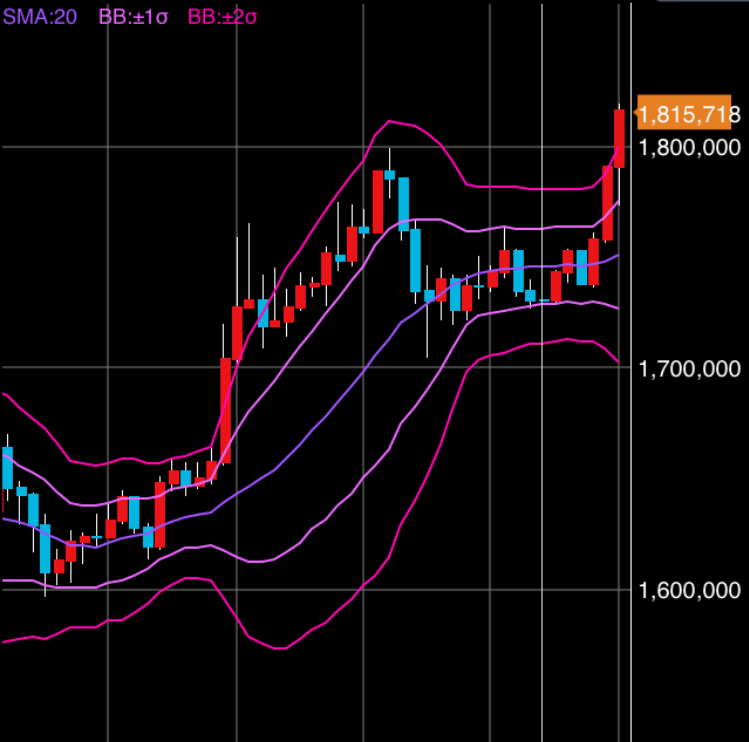
数学的な難しい話はさておき、ボリンジャーバンドにある根底の思想は次のように表現して良いと私は思います。
- 株や外貨などの金融商品の価格を瞬間ごとに追跡すると、うろうろと上がったり下がったりしており、そのままではノイズにまみれていて汚く扱いにくい。
- 瞬間ごとの価格からノイズを取り除きスムーズにした価格はなめらかで扱いやすい。
- 瞬間ごとの価格はスムーズ化した価格の近くをうろうろする事が多く、そこから大きく外れる事は少ない。
図1の例で言えば、ローソクのような赤と青の棒(そのまんまローソク足と呼ばれています)で示してあるのが瞬間ごとの価格を見やすく整理したもので、中央の紫色の線を縫うように上下しているのがわかります。この紫色の線が単純移動平均線です。紫色の線の周りにはラベンダーとマゼンタの各色の線がありますが、これらが1σと2σの線です。ローソク足は大体の時間において紫色の線とラベンダーの線のまわりをいったり来たりしていて、マゼンタの線にはほとんど触れないけどたまに突き抜けている事がわかります。
ボリンジャーバンドを用いた投資戦略とその弱点
ボリンジャーバンドの考え方では、単純移動平均線を基準となるスムーズな価格として採用し、標準偏差の線を価格がうろうろと基準の価格を行き来する幅として採用します。統計学的な前提として、価格が単純移動平均線から2σ以上離れる確率は5%ととても小さい事になっています。もし価格が2σの線を突き抜ける心配をしないのであれば、ローソク足が例えば下側の1σと2σの線の間にある時に、いま価格が下がっているがこれから上昇に転じるという予測が出来るので、投資対象を購入するチャンスだと捉える事ができます。このような値動きの逆転を期待する投資方法を、逆張りといいます。
また、ローソク足が例えば上の2σの線を突き抜けて大きく値上がりする事もあるだろうと考えるのであれば、突き抜けた瞬間に買い、十分に値上がりしたところで売る戦略が考えられます。
このような値動きの継続性を期待する投資方法を、順張りと言います。
どちらの場合も、現在の価格がボリンジャーバンドのどこに位置しているかによって投資行動を決める事が出来るので、ボリンジャーバンドを逐次計算しながら売り、買い、待ちの投資行動を行うプログラムを作れば良いことになります。
なるほど、それではそういうボリンジャーバンドのプログラムを作って投資すればよいではないか、と思うかもれませんね。ところがちょっとまって下さい。私達が目指しているのは10億円です。普通のボリンジャーバンドなんて多分誰でも使ってます。そんな方法でうまく行くと思いますか?誰でも使ってる方法だと、相場がいい時はみんなと同じように儲かり、相場が悪い時はやはりみんなと同じように損します。そんな方法は怖くて使えません。
さらに、ボリンジャーバンドにはどうしてもつきまとう二つの弱点があります。そしてその二つの弱点は値上がりも値下がりも激しいビットコインに使用するにはとても怖いものなのです。具体的には、
- ボリンジャーバンドはその滑らかさとトレンド検知の早さを独立に調整できないため、早いトレンドの変化に適切に追従できない
- ボリンジャーバンドはたまに起こる並外れた相場の急変を正しく理解できない
の2点です。これらを理解するためにはまず単純移動平均と各標準偏差の線がどのように計算されているかを知る必要があります。
ボリンジャーバンドの計算方法
まず単純移動平均線ですが、現在からローソク足5本分なら5本分、13本なら13本分過去にさかのぼって終値 (注釈 例えば一時間、一日、一週間などの期間を定め、その期間が終わった時点での価格の事を終値と言います) の平均をとる事で計算します。
また各標準偏差の線ですが、ローソク足一方分の、時間あたりの終値の変化量の二乗、つまりある終値とそのの直前の終値との差を二乗したものを、やはりローソク足5本分なら5本分、13本なら13本分過去にさかのぼって平均し、そして平方根をとったものです。
ちょっと複雑な気がしますが、統計学を学んだ事があれば、標準偏差の定義と似ていることがわかりますね。
目標1 曲線の滑らかさ、遅れの独立調整
どちらの指標も、現在から時間をさかのぼってデータを集めて集計しますから、今まさにこの瞬間の相場を表しているというよりは、少し前の時間における相場を遅れて現していると言えます。この遅れのため、トレンドの検出が遅れてしまう可能性があります。遅れを小さくしようとしてさかのぼる時間の量を少なくすればするほど、曲線のノイズは大きくなってしまいます。
一方、曲線のなめらかさを良くしようと、より長い期間さかのぼり終値を集め計算した場合が、長くした分だけ遅れが大きくなります。つまり、ボリンジャーバンドの曲線の滑らかさと遅れを別々に調整する事は基本的にはできないのです。
このため、短い集計期間ではノイズに惑わされて悪いタイミングで売買してしまう可能性があり、長い集計期間ではチャンスに乗り遅れてしまう可能性があるので、あちらを立てればこちらが立たずというわけです。
もし曲線の滑らかさとトレンドキャッチの早さを別々に調節出来る改良版ボリンジャーバンドを開発できれば、通常のボリンジャバンドでは立ち入る事のできない領域を探索、リスクのコントロールと高い収益性のがより高いレベルで両立できる設定を見つけられる可能性があります。これを実現する事が今回の一つ目の目的です。
ガウス分布
二つ目の弱点ですが、これは金融市場の統計的性質によるもので、ボリンジャーバンドの標準偏差の線の計算に関わるものです。
標準偏差はデータの集まりの値のばらつき具合を表すのによく用いられますが、その背後にはガウス分布というものがあります。
ではこのガウス分布とは一体なんなのでしょう?
ガウス分布はあらゆる場面において見出す事が可能なもので、例えばサイコロゲームの確率統計を考える時に利用ができます。
次のようなゲームを考えて見ましょう。
六面サイコロを転がして1,2,3が出たらプラス1点、4,5,6が出たらマイナス1点。これを一度のゲームで100回繰り返したら合計で一体何点でしょうか?予知能力でもなければ合計点を毎回ズバリ当てる事はできませんが、ガウス分布を用いればその確率を導く事ができます。
時間の都合上詳しい話は省きますが、ガウス分布を用いれば合計が-10点から10点の間に収まる確率や、-20点から20点の間に収まる確率など、必要に応じて点数の範囲に対応する確率を自由に計算する事が可能です。逆に、特定の確率からそれに対応する点数の範囲を計算する事も可能で、例えば68%の的中率でサイコロの合計値が当たる範囲を知りたいとき、それは-σ点からσ点である事が知られています。このσ(シグマ)が標準偏差、つまりサイコロの合計点の確率分布の幅です 図ガウス分布。
ところがこのガウス分布は残念ながら万能ではありません。例えばサイコロゲームのルールを少し変えて、百面サイコロの1-49が出た時にはプラス一点、50-98が出た時にはマイナス一点、そして99が出たときはプラス100点、100が出たときはマイナス100点。このようなルールでは単純なガウス分布を用いて正しくサイコロの合計値を正しく計算できません(この例で得られる確率分布は二つのガウス分布の重ね合わせで表せるので、本来話題としたいヘビーテール分布とは厳密には異なります)。なぜならガウス分布を用いる場合、サイコロの目に対する点数の絶対値は基本的にはどの目も同じである必要があるからで、このルールではその条件にそぐわないからです。(点数がマルチノミナル分布になっていれば多分同じ絶対値でなくても良いでしょう)
目標2 ガウス分布以外の確率分布の使用
実は金融市場にはこれと同じような問題があるため、ガウス分布でモデル化するのに適していない場面が度々見られます。なぜなら、百面サイコロの点数が出た目によって異なったように、金融市場は多種多様な投資家、会社、国家が関わる場所で、それぞれの相場への影響力は大きく異なるからです。例えば10万円程度でFXを楽しんでいる個人投資家が自己破産してもそれはサイコロ1の目が出たようなもので、相場は動じないでしょう。しかし、国家予算何兆円の国が財政破綻するのはサイコロの100の目がでたようなもので、その国の通貨はきっと暴落するでしょう。また、サイコロの目は人間の気持ちには関係なくランダムに出ますが、相場は色々な思惑や心理が錯綜する場なので、国家が毎日のように財政破綻するわけではないにしても、相場をガウス分布でモデル化しようとするとどうしても無理のある部分が出てきます。従って、価格が単純移動平均線から2σ以上離れる確率は5%以下と先ほど書きましたが、実はこれはあてに出来ない事も多いのです。
このような統計的性質をもつ金融相場をあえてガウス分布でモデル化すると、たまに起こる100の目のようなイベント(外れ値)にボリンジャーバンドが影響を受けて大きく広がってします。こういう事がたまたま単発で起こっただけならば、必要以上に気にせずにどっしり構えた方がかえってよい場合もありますが、ガウス分布が前提のボリンジャーバンドではそういう可能性は探索できないのです。しかし、ガウス分布の代わりに外れ値に耐性のある確率分布を用いれば、モデルが相場をより正しく理解できると期待できるので、リスクを抑えつつ収益を最大化出来る可能性があります。これを実現する事が今回の二つ目の目的です。
ガウス過程
これでようやく今回開発したい新しいボリンジャーバンドに求められ機能が明らかになりました。
- 各指標の曲線の滑らかさと遅れをを独立に調節出来る
- 外れ値に耐性のある確率分布を用いて値動きの幅σが計算可能
これらが可能な機械学習アルゴリズムとして、ガウス過程を使用します。時間の都合上詳しい説明は次回に回しますが、ガウス過程を簡単に説明すると、どんな関数でモデル化するべきかわからない時にも回帰分析ができる(ノンパラメトリック回帰)アルゴリズムで、 ガウス分布に限らずあらゆる確率分布を使用する事が可能なものです。関数をほぼ自動で関数のプールから探してくれる事と、確率分布に強い事から、ベイズ最適化などに用いられ、ディープラーニングのハイパーパラメーターチューニングなどの難しい作業の自動化に役立てられています。今回はガウス過程のライブラリとしてこれを用いて実験を行いました。また、外れ値に強い確率分布としてt分布を使用するために、特別な最適化手法(注釈 この手法はstabilised Newton’s method や Rasmussen’s mode finding などと呼ばれていますが、ガウス過程でこの手法を用いる例は少なく、文献の記述も限られています。これが実装されているライブラリはGPML, pygp, GPstuffなどで、今回はこれらを参考に実装しました)を新たに実装しました。
結果
それでは早速これを使って単純移動平均線の代わりとなるもの、GP移動線とでも呼びましょうか、を計算してみましょう。曲線の性質はガウス過程の心臓部であるカーネル関数と呼ばれるものので指定し、このカーネル関数のパラメーターを調節する事で曲線の滑らかさを調節します。今回はRBFと呼ばれるもカーネル関数を用います。また、ビットコインの価格はhttps://www.kaggle.com/mczielinski/bitcoin-historical-dataからダウンロードしたものを使用し、概ねいついつの期間のデータを適当に切り取り用いました。
下の図3つがガウス過程でモデル化したビットコインの価格です。
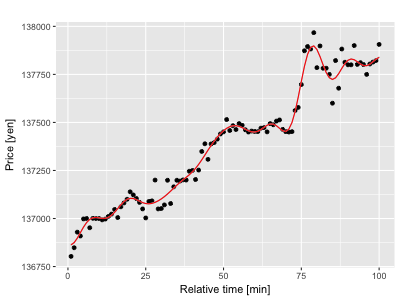
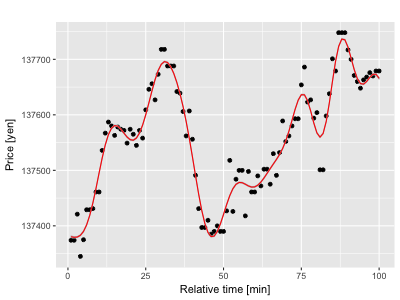
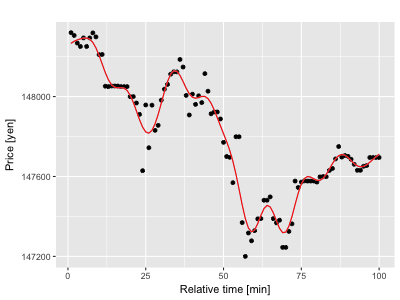
どの図も実際の価格によくフィットしているように見えます。驚くべきは、これらのモデルはどれもとても異なって見えるにも関わらず、使用したガウス過程のモデルは一切変えておらず、インプットとなる価格のみが異なるという事です。
今度はガウス過程のハイパーパラメーターを変えるとどのように曲線が変化するかを試してみましょう。
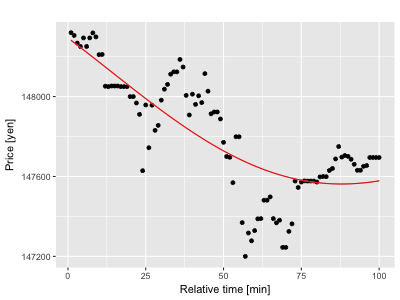
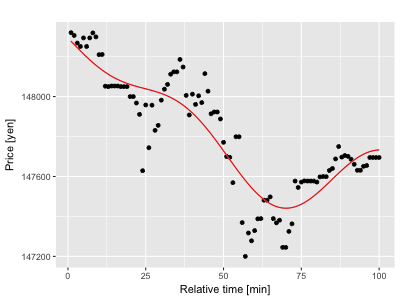
パラメーターlを調節すると、曲線のうねり具合が変わる事がわかります。このlを用いれば、単純移動平均線のデータ集計期間を変える事で曲線の滑らかさを調節したのと同じように、データの細かい構造をモデルをトレースさせるか、あるいは大まかな形を反映させるかを調節できそうですね。このモデル曲線の最新の時刻に相当する、一番右端の点をその時刻のGP移動線に採用すれば、GP移動線の遅れは0となります。このような、モデルの計算とアウトプットから点の採取を、期間を少しづつずらしながら繰り返せばGP移動線を作る事ができます。
次に標準偏差の計算を行ってみましょう。通常は上記の式を用いますが、今回は線形回帰分析を用いて同様な事をやってみます。ガウス過程は関数を指定しない回帰だけでなく線形回帰などもできます。ガウス分布を用いてノイズをモデルすると、
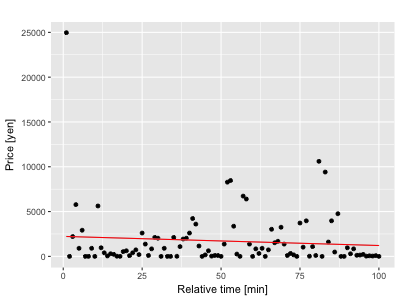
回帰直線がデータポイントが最も多くみられる場所よりも幾分上向きに引っ張られているのがわかります。一方、外れ値に強いt分布を用いると、
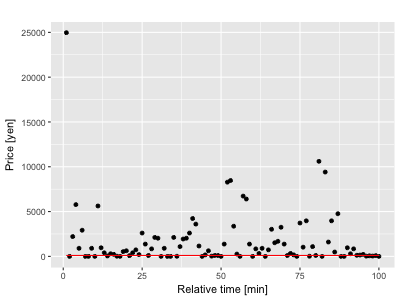
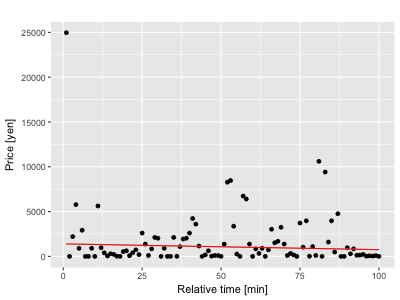
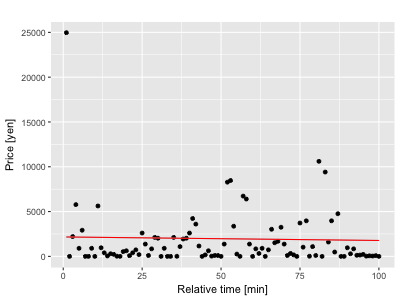
一番上の図では回帰直線はビタッとデータポイントが一番集まっている下側に出る事がわかります。さらに、t分布のハイパーパラメーターを調節してやる事で、中央と下にあるように外れ値への耐性を調節する事ができます。
結論
今回はガウス過程を用いてボリンジャーバンドの改良に挑戦しました。その結果、通常のボリンジャーバンドではできない曲線の滑らかさと遅れを独立にできる事と、外れ値に耐性のある確率分布を標準偏差線の計算に用いる事が可能な事がわかりました。次回は今回開発したアルゴリズムを利用して取引のシミュレーションに挑戦したいと思いますので、ご期待下さい。
求人
次世代システム研究室では、機械学習や統計処理に関心を持つ開発者、アーキテクト、データサイエンティストを求めています。
自由闊達にのびのびと働きながら学べる環境が、コーヒー片手にアカデミックとビジネスの融合したディスカッションをしながら、知的好奇心を満たすことができる環境があなたを待っています。
次世代システム研究室にご興味を持たれたらすぐに 募集職種一覧 からご応募してください。
皆さんのご応募をお待ちしています。
自由闊達にのびのびと働きながら学べる環境が、コーヒー片手にアカデミックとビジネスの融合したディスカッションをしながら、知的好奇心を満たすことができる環境があなたを待っています。
次世代システム研究室にご興味を持たれたらすぐに 募集職種一覧 からご応募してください。
皆さんのご応募をお待ちしています。
グループ研究開発本部の最新情報をTwitterで配信中です。ぜひフォローください。
Follow @GMO_RD

